Lopez de Lacalle L.N., Lamikiz A. Machine Tools for High Performance Machining

Подождите немного. Документ загружается.

10 Parallel Kinematics for Machine Tools 345

In the last paragraph the reader may have noticed that the term subsets is used

instead of subgroups; this is because those displacements do not fulfil some property

of the Lie group. This issue imposes some limitations on the method regarding the

difficulty to find all possible motion generators of the displacement desired and its

validity for finite displacements.

10.4.3 The Position Analysis

Once a mechanism has been synthesised, the following step is to state the equa-

tions that locate the pose of the end-effector for given inputs, called the direct

kinematics problem; and vice versa, those equations to provide the inputs needed

for a given pose, called inverse kinematics problem. These equations are used in

the position control, either to monitor the pose or to generate orders to the actua-

tors. As opposed to serial mechanisms, while the inverse kinematics problem is

trivial for many parallel mechanisms, the direct problem is in most occasions very

challenging.

In order to get the system of position equations, methods such as Denavit-

Hartenberg’s used in serial kinematics are complicated by the existence of multi-

ple closed loops. Therefore, it is very common to employ the so-called “geometric

method”. In this approach, a vector-loop equation

()

0pq,x,g = is written for each

limb and constraint equations are added for lower mobility parallel manipulators.

These equations relate the pose of the end-effector x, the inputs q, and the passive

variables p. Then mathematical manipulation tries to get rid of passive variables to

arrive to a reduced system of equations

()

0qx,f = relating only input and output

variables. In this system f are n-dimensional implicit functions of n-dimensional

vectors x and q (n being the number of DOF).

Unfortunately, the resultant system of equations is a set of non-linear equations

often including sine-cosine polynomials. As most research into non-linear equa-

Ł Ł =

}·{R

} Ł {T

}·{R

} Ł {T

}·{T

}·{R

}={T

}·{T

}·{R

}

Fig. 10.6 Displacement subsets intersected to get the motion desired in model Verne™

346 O. Altuzarra et al.

tions solving is on algebraic polynomials, it is also common to transform sine and

cosine into variables. These systems have generally multiple solutions, some real

and some imaginary, being not always able to be solved analytically. Closed form

solutions are rare in parallel machines; at best an univariate polynomial is obtained

and then solved numerically, and often the multivariate polynomial system has to

be solved numerically from the very beginning. On the one hand, when looking

for all real solutions to the problem, some methods deserve a mention: polynomial

continuation and homotopy continuation methods, elimination methods, Gröbner

basis technique, and resultant methods [33]. On the other hand, if only one solu-

tion is sought and this is properly cornered by a closed approximation obtained

with external data, mechanical constraints or other means, it is very common to

use a Newton-Raphson’s procedure. This procedure is quick enough in most cases

as it has a quadratic convergence when starting with a good approximation. More-

over, there are several techniques to test its convergence, like Kantorovich’s,

which help in giving enough reliability to this method for use in the control. The

last method is commonly applied in parallel kinematic machines to generate the

kinematic transformation needed in the CNC. A more detailed analysis of these

methods is beyond the scope of this book.

On the one hand, the position problem is used as mentioned above. Due to the

parallel configuration of the PKMs, there is a non-linear relation between the posi-

tion values of the drives and the position value and the tilt angles of the platform

that carries the spindle. From the control point of view, this relationship is repre-

sented by a mathematical model that simplifies the mechanical system to a com-

putable degree. The implementation of this model inside the numerical control is

called kinematic transformation. The model describes only the rules of the relation

between the ingoing and outgoing variables of the system.

On the other hand, for design purposes, a very useful and practiced strategy in

the industry is to use commercially available CAD packages to perform the posi-

tion analysis [4]. The main advantage of these packages is that there is no need to

write the equations as described previously. It is enough to introduce the joints, as

determined in the synthesis stage, in the correct position and the software is able to

determine the DOF.

The limitation of these packages is that they only provide the number of DOF,

but not their nature (rotation or translation), so a prior knowledge of the type of

the DOF is needed. However, if the number and type of DOF is known, a com-

plete position analysis can be performed.

One of the objectives of the position analysis is to obtain the working volume

maintaining the restriction of the joints (rotation limits) and avoiding collisions

between elements. For this latter purpose, CAD software packages are very useful

because they usually include a collision detection algorithm. Figure 10.7 depicts

a PRO/Engineer model of the Verne machine.

A position analysis was performed in this machine, in order to determine the

working volume of the machine. Usually the size of the working volume is a re-

quirement, so the machine dimensions are changed iteratively in order to obtain

the working volume considering the body interferences and the joint limits. Also,

10 Parallel Kinematics for Machine Tools 347

the working travel on the axes, i.e., maximum and minimum values, can be found

with the same technique.

A differentiation has to be made between the working volume and the work-

space of the machine. The first one is the volume reachable by the tool, while the

second one is a more complete concept. It refers to the positions reachable and the

range of rotation attainable for each position. This space is not easy to represent.

The knowledge of the work space is very useful for the further analysis of vel-

ocity, accelerations, singularities or manipulability, above all if an iterative proc-

ess is to be used.

10.4.4 Velocity Analysis, Singularities and Dynamics

Analogously to position problems, there are two types of velocity coordination

problems: the direct velocity problem, that solves the velocity state of the end-

effector given the input rates, and the inverse velocity problem, that does vice

versa. In order to get the velocity equations, there are several approaches. One is

the differentiation of the position equations, i.e., loop-closure equations and con-

straint equations. Another is the use of screw theory to get the velocity equation.

Both methods generate an input-output velocity equation characterised by the so-

called Jacobian matrices.

Fig. 10.7 PRO/Engineer model of Verne™ machine (by Fatronik

)

348 O. Altuzarra et al.

The analysis of the singularity of these Jacobians is a way to detect the singu-

larities of these manipulators [33]. Several classifications of singularities have

been issued [14,

53]. The common point is that the singularity is a posture where

the control will have a problem to control the end-effector and must be avoided.

Mathematically, singularities arise at certain specific configurations of the mecha-

nism, but in practice, due to backslash and assembly errors, the singularity will

occur in an area around that specific posture. Therefore, it is very useful to get

indicators of proximity to singular configurations and restrict the motion to areas

with acceptable values of such indicators. These numerical parameters are some-

times tricky and require deep mathematical analysis [33].

Acceleration and jerk analysis can be performed in successive derivations of

velocity equations. In relation to them, dynamic analyses are also performed. To

do this, classical dynamic methods can be used for ad-hoc analysis of a certain

manipulator while multi-body methods can be used for CAE evaluation of virtual

designs. Such an analysis will provide the tools to determine the material and

sections of links, as well as the drives needed for acceleration requirements.

Again, a practical approach is the use of the latter CAE software packages that

implement multi-body methods to get kinematic and dynamic equations. Once the

dimensions of the machine are defined and the desired working volume is reach-

able, iterative analysis of speeds, accelerations and singularities can be performed.

For this analysis, it is possible to use the same packages used to perform the

position analysis. In the Verne machine of Fatronik, different trajectories have

been analysed, like linear motions, circular interpolations and angular rotations,

obtaining velocities and accelerations values in the motors.

Singularities can also be analysed with the commercial CAD packages but only

to a certain extent. Like the situation with the mobility, they do not provide infor-

mation about the type of singularity, but just some warning messages.

Velocity on Y rotation (deg/s)

-0,15

-0,10

-0,05

0,00

0,05

0,10

024681012

Time (s)

Rotation speed (deg/s)

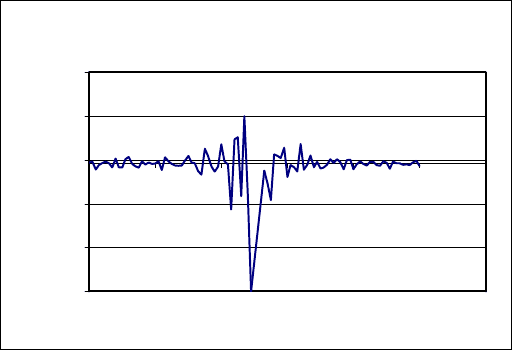
Fig. 10.8 Velocity profile in the analysis for singularity

10 Parallel Kinematics for Machine Tools 349

For example, if a PRO/E representation of the mechanism is used for the analy-

sis of singularities, and the mechanism has an inverse kinematic singularity, i.e.,

several inputs become dependent. The velocity profile of some axis will be altered

in the proximities of the singular point as seen in Fig. 10.8. Also, the program

reports a problem assembling the mechanism only when the position is close to the

singular configuration. As shown no specific information on the singular points is

provided; however it helps to detect possible problems in the mechanism.

10.4.5 The Optimisation

Previously to develop the design further, an optimisation analysis can be made.

The objective of this study can be very different: minimising the torques on the

drives or reducing the size of the machine. Commercial packages implement op-

timization processes with maximisation or minimisation objectives. This objective

can usually be defined as a function, depending on geometrical parameters, or on

measures (position, torques, speed, and so on), giving a high flexibility in order to

design an optimal mechanism.

These optimisation tools have been applied to the design of the Verne machine

to obtain the desired working volume with the minimal machine footprint. The

optimisation has been made taking into account only geometrical parameters:

• The position of joints in the supporting frame. In order to maintain the DOF

a relationship between some of the parameters is fixed.

• The length of the struts.

• The distance of the first axis of the tilting table (A axis) to the origin of the base

coordinate system.

The objective of the minimisation is defined as a function, in this case the shop

floor used surface. This function is defined based on two basic features of Pro/En-

gineer, the distance between two planes. The product of these two distances gives

the surface of the machine, and this value has been set as the objective function.

Multi-objective optimisation is more difficult; it seeks the simultaneous optimi-

sation of several functions that sometimes are opposite. There are very few works

on this subject and it is an open problem; an approach could be to adapt techniques

used in structural analysis such as the Pareto front based methods.

10.5 The Kinematic Calibration of PKMs

After the design process, the first prototype can be manufactured and several ex-

perimental tests should be carried out to check the correct assembly. After that, the

control that implements the theoretical kinematic transformation has to be adjusted

350 O. Altuzarra et al.

to the actual dimensions and assembly of the machine. For that purpose a calibra-

tion procedure has to be applied.

Because of the kinematically non-linear behaviour of PKMs, common methods

for calibration like the adjustment of axes and setting the zero point cannot be

applied. Parallel kinematics’ axes can not be adjusted one by one, but need to be

looked at as a complete system of coupled ingoing and outgoing values. This can

be compared to the parameter-identification of any complicated system, for exam-

ple a controlled system, which has to be identified. The system parameters that

have to be identified here are the zero points, beam lengths and numerous different

geometrical parameters that characterise the kinematical behaviour of the ma-

chine. To make the model fit as closely as possible to reality, we have to adjust

these parameters; this adjustment is called kinematic calibration.

Though these values are all specified in the design drawings of the machine we

still need to determine them by calibration. The manufacturing and especially the

assembling tolerances of the parts of the motion mechanism can never be made

small enough to spare calibration.

Calibration is always the determination of parameters of a model that describes

a real system of any physical nature. The goal of this procedure is always to make

the model behave as closely as possible to the real system itself. The principle of

each calibration is to record the input/output-behaviour of the system and based on

these recorded values fit the model to reality so that it simulates the input/output-

performance of the modelled system.

Calibration is a well known problem for serial robots and conventional machine

tools, and now it is a well-treated problem. It may be thought that the calibration

of parallel robots may rely on the methods developed for serial morphologies but

unfortunately this is not exactly the case. Indeed there is a major difference be-

tween both mechanisms: for serial ones small errors on the geometrical parameters

induce large errors on the positioning of the end-effector, while for parallel ma-

chines these errors will also be small. Simulation for calibration is essential: it

allows determining how much a calibration method is sensitive to noise in the

measurements and to numerical errors. It allows for example to show that methods

directly adapted from the calibration of serial robots may lead to results that are

worse than the initial guess as soon as the simulated measurement noise is realistic.

There are two types of calibration methods:

• External: an external measurement device is used to determine (completely or

partially) the real position of the platform for different desired configurations of

the platform. The differences between the measured pose and the desired pose

give an error signal that is used for the calibration.

• Self-calibration: the platform has extra sensors (sensors that can be used to

solve other problems like the forward kinematics) and only the information of

these extra sensors is used for the calibration.

The procedures of the first type tend to be difficult and tedious to use in prac-

tice but may give good results. The second method may be less accurate but is

easy to use and has also the advantages that it can be fully automatised.

10 Parallel Kinematics for Machine Tools 351

Calibration has two important aspects. On the one hand, we have the mathe-

matical approach: (i) a selection of parameters for calibration, (ii) measuring

machine configurations and (iii) a method for estimating the new machine pa-

rameters. On the other hand, it is the determination of (i) the external measure-

ment artefact or (ii) the number and type of sensors (self-calibration).

10.5.1 A Mathematical Approach

Concerning the selection of parameters for calibration, the most common approach

is to select those controlling the kinematic transformation of the machine. As the

kinematic transformations are very different depending on the kinematic structure

of the machine one may conclude that the calibration models are very different

depending on the machine. However, reality shows that most of the parameters

that rule the kinematic model are the same for most machines, such as the position

of joints, the lengths of struts and the encoder offsets.

It is typical that models comprise simplifications. The mathematical model that

the control uses to transform positions into drive values assumes that the motors

move along absolutely straight lines. It is relatively difficult to model the move-

ment in a more appropriate way, so we have to be aware of the fact that we might

introduce errors here. Moreover we disregard the fact that universal joints perform

a motion that might differ considerably from moving around an infinitely small

point. Elasticity, clearance and elongation due to varying temperatures are not

represented at all in the models.

Though it is partly possible to measure certain parameters directly, this is

not necessary and not even reasonable. Because of all the simplifications the

model contains, the values of the parameters will not be assigned in exact ac-

cordance to their physical values. Instead they will be adjusted by the algorithm

in a way that makes the model as a whole fit reality as closely as possible. So

the values often differ significantly from what would be determined by direct

measurement.

The calibration minimises the difference between the output of the model and

the output of the real machine. The input is the same for both. It is important to

realize that the result of this optimisation is optimal in respect to the measurement

values that have been gathered. To ensure that they are good in respect to the

whole workspace and applicable under common working conditions, certain pre-

conditions have to be kept. As a logical consequence of this it is clear that the

platform poses that are measured have to be chosen deliberately.

The idea of the pose selection is to extract the points of the working volume

that result in the most accurate estimates. For some poses, the parameters of the

kinematic model do not influence the measurements much: the effects of meas-

urement noise and un-modelled sources of error dominate over the effect of the

variation of the kinematic parameters of the structure. As a result, the calibrated

parameters obtained will not be reliable.

352 O. Altuzarra et al.

Researchers have proposed a variety of observability indices to quantify the

goodness of pose selection; these indexes area based on the singular value decom-

position (SVD) of the Jacobian matrix of the differential kinematics. Menq and

Born [32] proposed an observability index related to the product of all singular

values. Driels and and Pathre [12] proposed the condition number; Schroer et al.

[46] stated that a condition number below 100 is required for reliable results.

Nahvi et al. [35] proposed the minimum singular value. Hollerbach and Nahvi

[36] proposed the noise amplification index, defined as the ratio of maximum

singular value to condition number. Daney et al. [11] proposed a method based on

the identification Jacobian, combined with a meta-heuristic approach to decrease

the sensibility to local minima. The last method applies also to Gough platform

calibration.

Other issues that sometimes appear are related to the presence of redundant pa-

rameters during the calibration. This term applies to the fact that the error of two

different parameters of the kinematic model translate into the same measured

error, causing a poor estimation in the parameters. Meggiolaro and Dubowsky [31]

proposed an analytical method to eliminate the redundant parameters in calibra-

tion. The method is based on the non-singular of the Identification Jacobian matrix

using the D-H parameters.

From the mathematical point of view, kinematic calibration reduces to obtain-

ing the unknown parameters of set of non-linear functions (the kinematic trans-

formation) evaluated at a discrete number of points (measuring poses) with a very

good estimation of the function parameters (theoretical machine configuration).

This problem is already solved and is known as the non-linear least squares problem.

However there is an important aspect to be considered in this approach: there is

noise in the measurement. If this noise is too high, the resulting fitting problem

can be useless, and the estimated parameters very bad.

Another aspect to take into account during calibration is the presence of errors

due to the reduced DOF of the kinematic structure. In the case of the Gough/

Stewart platform or 6 DOF parallel kinematic machines, if other sources of error

are neglected (thermal effects, deformations due to gravity, measuring errors ...)

the calibration will obtain zero error in position and orientation. This is true since

the number of controlled DOF is the same as the possible sources of error of the

platform: three translations and three rotations.

Parallel kinematic machines with reduced DOF use passive constraints to

eliminate the non-desired DOF. Due to machining and assembly errors, it is very

likely that these passive elements induce some error in the same DOF that restrict,

or in the worst case in a controlled DOF. For example a three DOF Cartesian ma-

chine with passive elements for angular rotations will have some deviations be-

tween the desired fixed orientation and the real orientation.

The problem is that the kinematic model cannot compensate for these angular

errors, since the orientation is uncontrolled, and as a consequence calibration is

not possible, so a remaining error is present. Even worse, if the rotation error in-

duces a displacement in the X direction for example this error will affect the calibra-

tion, producing in some cases strange results in the parameters. Passive elements

10 Parallel Kinematics for Machine Tools 353

must be carefully controlled in precision, reducing the errors to the minimum

during the assembly process, or measuring the magnitude of the errors and taking

into account the calibration process.

10.5.2 Measuring on External Methods

The measuring stage of the calibration is not 100% independent from the already

common aspects of the mathematical approach. The pose selection and adjusted

parameters can limit the number of applicable measuring methods. Another aspect

is that with the commercially available systems, it is not possible to measure at the

same time the six coordinates. In fact, the lower the number of simultaneous

measurements, the better the measuring precision. Some typical TCP measuring

devices are:

• The laser tracker.

• Photogrammetry, vision.

• The double ball bar.

• The grid encoders.

• Dial gauges plus extra fixtures.

• The reference piece plus touch probes.

• Others (inclinometers, accelerometers).

The choice of the measuring apparatus must be done taking into account the

following criteria:

• The precision of the measuring device (above all).

• The time needed for measuring (degree of automation).

• The qualification required for the measuring device user.

• The limitation on measuring range.

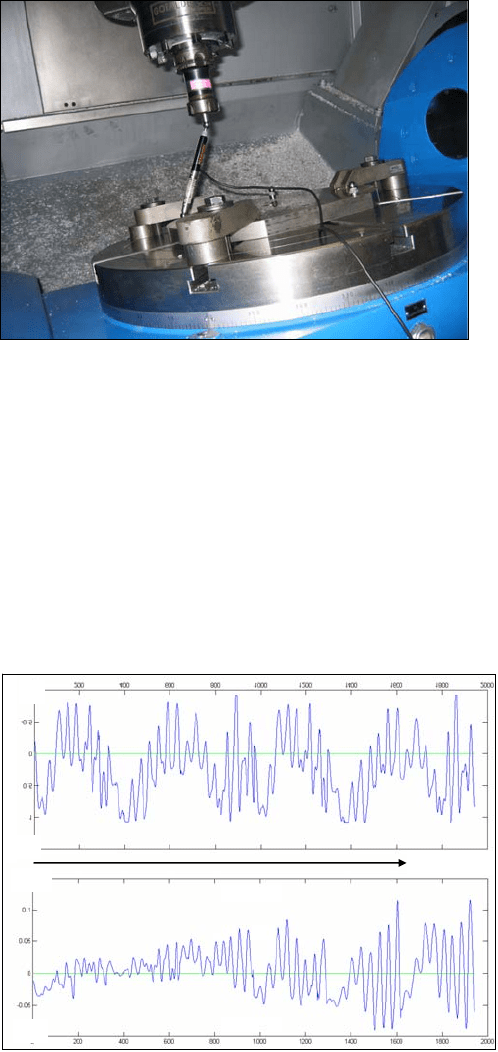
Figure 10.9 shows the calibration method for the Verne machine [44]. The calibra-

tion strategy uses a double ball bar from Renishaw

, a commercially available ele-

ment. Combining this element with a calibrator provided also by Renishaw, it is pos-

sible to measure the absolute distance between the centres of two calibrated spheres.

The calibration procedure measures the distance (150

mm theoretical) between

three spheres placed in a known position in the tilting table (measured with

a MMT) and a sphere placed in the centre of the tool holder. The machine moves

along a set of points that covers the entire working volume in position and rota-

tion. Two tool lengths are used to measure the distance between the spheres, so

sets of measurements are obtained, making a total of 1944 measured points.

The upper part of Fig. 10.10 shows the errors of the programmed 150

mm dis-

tance on the calibration process. As shown there is a maximum error of 1

mm. The

lower part shows the verification of the machine precision of the calibration. The

error is now less than 5% of the starting error in most of the points, with a maxi-

mum of 10% in some extreme positions.

354 O. Altuzarra et al.

A similar method to the described is used to calibrate the Space-5H machine.

Once the programs files are created and the procedure standardised, a complete

machine calibration can be performed in 5h by a machine user. The main limita-

tion of this method is the range of measure of the ball bar, limited to

±1

mm.

However, this problem only appears in the first calibration after assembly, but not

in the recalibration process, so this is not a problem for the end user.

This method is an example of external calibration methods. Another calibration

strategy that uses a ball bar is found in [39]. In this case it is applied to the calibra-

Fig. 10.9 Calibration test bed for Verne™ PKM

0.15

-0.1

-1

1.2

2000 mm

Fig. 10.10 Error results (in mm) of the calibration in the Verne™ PKM