Лобанов А.Н. Фотограмметрия

Подождите немного. Документ загружается.

§ 57. Зависимость между координатами

соответственных точек горизонтального и наклонного снимков

Получить строго горизонтальные снимки в процессе аэрофото-

съемки пока невозможно. Однако можно перейти от координат

точки, измеренных на наклонном снимке, к координатам соответст-

вующей точки горизонтального снимка, если известны угловые

элементы внешнего ориентирования наклонного снимка.

Пусть х° и у

— координаты изображения а° точки А местно-

сти на горизонтальном снимке Р°, полученном с точки 5 (рис. 125),

ахи у — координаты изображения а

той же точки на наклонном снимке

Р, полученном с точки 3.

р!»Применив формулы (9.11), напи-

шем

Х-

-2з)

а, (х-

(2 -

(У

—

= (2-

Уо)

—

з1

(х — х

) + с

[у

•

у-Уз= ~{2-2з)

л!

-Уо)—Сз!

= (2-

У°

Рис. 125

(х — х

) + а

(у-

-2з)

Отсюда

- У

о)

— аз/

(х — х

) -|-Ь

(у — у

) — 6

(X — х

) +С

(у— у

) — С

—

)

+ с

(у —

г/о)

— с

К (х — х

) + Ь

{у— у

) —

(9.27)

(х

—

о)

+ с

(у —

(/о)

—

Сз/

Эти формулы трансформирования координат пригодны при любых

значениях угловых элементов внешнего ориентирования снимка.

Преобразуем их для планового снимка, подставив значения направ-

ляющих косинусов из равенств (9.9),

о = —/[лг — (1/2) ха

— (1/2) хх

— ух— уа со + /а] X

X [ха + хсох + у<о—уам—Г + (1/2) /а

+ (1/2) /со

или

= \х+ 1а—ух - (1/2) ха? — (1/2) хх

— {/асо] X

X [

— *//а + у//со + 1/2а

+ 1/2со

— (<///) ах + (*//) сох]-

Известно, что

(1 — е)-

= 1 + е+е

+ . . .

Поэтому

х®

= [х

/ос •—

ук — (1/2) ха

— (1/2) хх

— уат] [1 + (*//) а +

+ (У К)

а>

+ (1/2) а

+ (1/2) со

(уЦ)

ах + (*//) сох +

+ (х

) а

+ (у*1[

) со

+ (2ху1}

) асо].

150

После перемножения получим

х° = х (/ + хЩ а + (хуЦ) со - ух + *

+ *

//) «

+ * (1/2 + уЧР) со

— (1/2) хх

+ (2Л:

) асо —

—

(2хуЦ)

ах + (х

- у

//) мх. (9.28)

Аналогично найдем и координату

= У + {хуЩ

+ (/ + у*Ц) 4, + хх + у (1/2 + х

) а

+ У (1 + г/

) со

- 1/2г/х

+ х (1 + 2г/

) асо +

+ (х

- г/

//) ах + (2x1///) сох. (9.29)

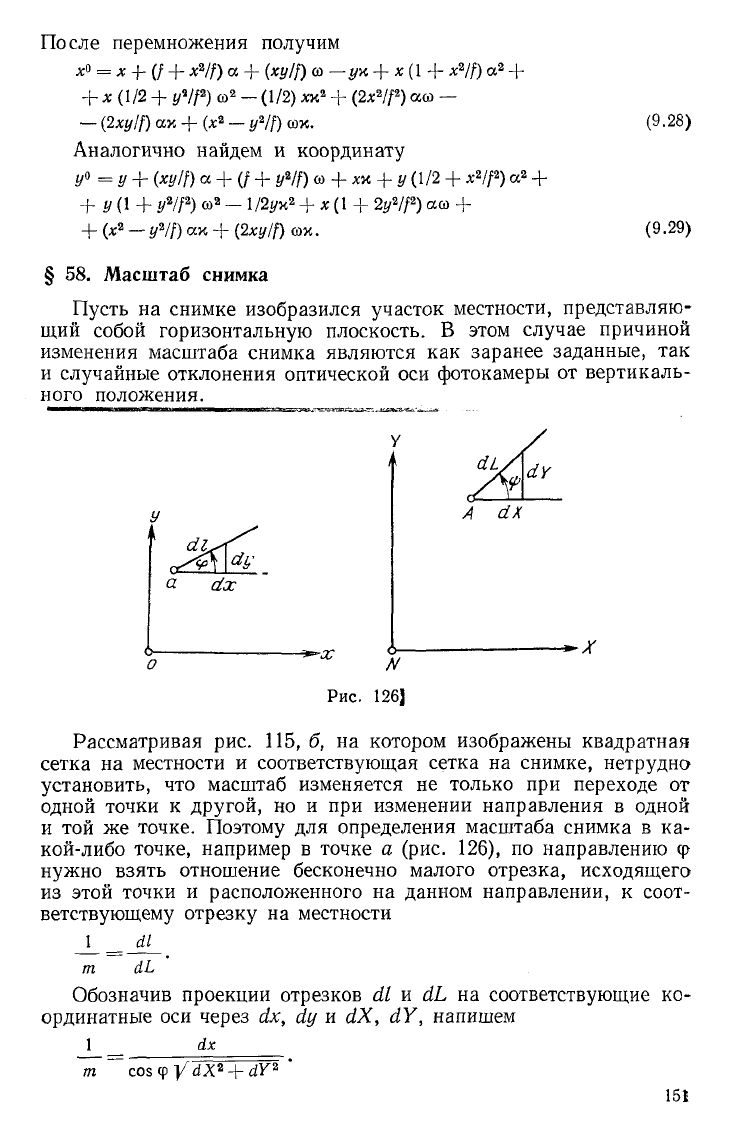
§ 58. Масштаб снимка

Пусть на снимке изобразился участок местности, представляю-

щий собой горизонтальную плоскость. В этом случае причиной

изменения масштаба снимка являются как заранее заданные, так

и случайные отклонения оптической оси фотокамеры от вертикаль-

ного положения.

-X

•X

Рис. 126]

Рассматривая рис. 115, б, на котором изображены квадратная

сетка на местности и соответствующая сетка на снимке, нетрудно

установить, что масштаб изменяется не только при переходе от

одной точки к другой, но и при изменении направления в одной

и той же точке. Поэтому для определения масштаба снимка в ка-

кой-либо точке, например в точке а (рис. 126), по направлению ср

нужно взять отношение бесконечно малого отрезка, исходящего

из этой точки и расположенного на данном направлении, к соот-

ветствующему отрезку на местности

_1_ _ й1

т ЛЬ

Обозначив проекции отрезков 6.1 и ё,Ь на соответствующие ко-

ординатные оси через (1х, с1у и йХ, йУ, напишем

1 йх

соз ф УйХ

+ аг*

151

Теперь используем формулы (9.15), выражающие зависимость

между координатами соответственных точек а и Л. После диффе-

ренцирования этих выражений по переменным х и у найдем

„/соз«о—узшар + хзтао^Ф ,

ал — п — ах;

(/ соз а

— у зт а

)

йУ = н

- Ш = н ^ ах.

(/соза

— у зт а

)

(/соз а„—г/зта

)

Учитывая значения йХ и йУ, после простых преобразований

окончательно получаем

1 Г

— = -77- к

[ (к соз Ф + с зт Ф)

+ 31п

ФР

1/2

, (9.30)

т И

где

к — соза

— ^у^вша,; с = (9.31)

являются постоянными величинами для данной точки снимка.

Таким образом, масштаб снимка зависит от высоты фотографи-

рования, фокусного расстояния фотокамеры, угла наклона снимка,

положения точки, в которой взят бесконечно малый отрезок й1,

а также от направления этого отрезка.

Направления ср

, соответствующие максимальному и минималь-

ному значениям масштабов в данной точке снимка, можно найти

по формуле

^§2ф

= 2кс/(к

— с

— 1), (9.32)

которая получается из выражения (9.30) по известному из матема-

тики правилу определения предельных значений функции.

Пусть от какой-либо точки снимка по различным направлениям

отложены соответствующие значения масштабов. Из математиче-

ской картографии известно, что линия, соединяющая концы по-

строенных таким образом отрезков, представляет собой эллипс

масштабных искажений. При этом большая и малая полуоси эл-

липса изображают предельные значения масштабов в данной точке.

На рис. 127 показан снимок, в различных точках которого по-

строены эллипсы масштабных искажений. Размер снимка 24 X

X 18 см, а

= 30°, х = 0, / = 200 мм. Значение масштаба в точке

нулевых искажений принято за единицу. Такое построение, назы-

ваемое индикатрисой масштабных искажений, дает наглядную

картину изменений масштаба в пределах всего снимка.

Для снимка, имеющего другие значения угла наклона и фокус-

ного расстояния, индикатриса масштабных искажений несколько

отличается от представленной на рис. 127, однако общий характер

распространения искажений сохраняется.

Найдем по формуле (9.30) значения масштаба снимка для раз-

личных частных случаев.

152

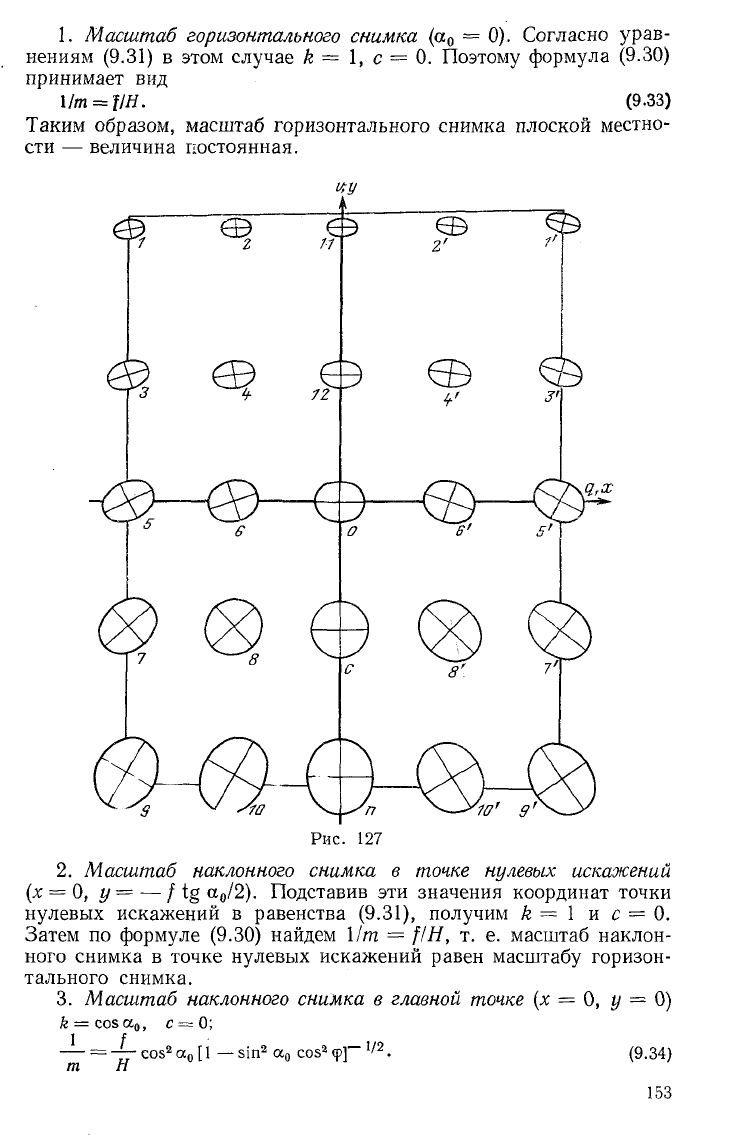
1. Масштаб горизонтального снимка (а

= 0). Согласно урав-

нениям (9.31) в этом случае к = 1, с = 0. Поэтому формула (9.30)

принимает вид

11т = ЦН. (9.33)

Таким образом, масштаб горизонтального снимка плоской местно-

сти — величина постоянная.

цу

2. Масштаб наклонного снимка в точке нулевых искажений

(х = 0, у = — / а

/2). Подставив эти значения координат точки

нулевых искажений в равенства (9.31), получим к = 1 и с — 0.

Затем по формуле (9.30) найдем

!т = т. е. масштаб наклон-

ного снимка в точке нулевых искажений равен масштабу горизон-

тального снимка.

3. Масштаб наклонного снимка в главной точке (х = 0, у = 0)

к = соза

, с = 0;

— = ТГ

С052 а

—

п2 а

о соз

<р]

'. (9.34)

т Н

153

Отсюда следует, что масштаб в главной точке меньше главного

масштаба. Этот вывод демонстрирует и рис. 127.

4. Масштаб в точке надира (х — 0, у = — / а

)

к = 1/соз а

, с = 0;

(1 —зт

а„зт

ф)-^. (9.35)

т Н соз а

Это выражение показывает, что масштаб в точке надира крупнее

главного масштаба.

5. Масштаб по направлению главной вертикали (х = 0, ср = 90°)

1 / / У V

— = —

С05К

— 8Ш

) , (9.36)

т Н \ / )

т. е. изменяется при переходе от одной точки этой линии к другой.

6. Масштаб по направлению горизонтали (ср = 0)

1 1С У \

— = — ^соза

— зт а

•

(9.37)

Следовательно, масштаб данной горизонтали (у = сопз!) — ве-

личина постоянная.

Масштаб главной горизонтали (у = 0)

— =— соза

. (9.38)

т Н

7. Масштаб планового снимка. Угол наклона планового снимка

обычно мал. Поэтому равенства (9.31) можно представить в таком

виде:

к =

1 —

(<///) «0. с= (х//) а

Подставив эти значения к и с в формулу (9.30), получим масштаб

планового снимка в произвольной точке по направлению <р

— = (//Я) {1 - («„//) [у (1 + 5Ш

Ф) + (1/2*) зт 2

]}. (9.39)

Теперь найдем средний масштаб планового снимка в произволь-

ной точке [2]

-1- = ± (1 _ [ у(

_2_ }"

щ« фйф) +

ср

Н [ { Г V 2я Й

V ^

2Я

1 г 1

+ х\ зт2фйф

4л о ] )

Так как

2л 2я

I 51п

фйф= | (1/2ф—1/2 3)П ф соз Ф) = я, а

о о

2л 2я

| 31П 2ф^ф = | 1/2соз2ф = 0, то

р Н

154

Рассмотрим две горизонтали на плановом снимке, определяе-

мые координатами у = ± а (рис. 128). Как следует из выражения

(9.40), средний масштаб в точках первой горизонтали (у = а) от-

личается от среднего масштаба в точках второй горизонтали

(у = — а) и от главного масштаба снимка / : Я. Однако среднее

арифметическое из средних масштабов для этих двух симметрич-

ных горизонталей равно главному масштабу снимка. Поэтому

можно считать, что средний масштаб

планового снимка в зоне, ограничен-

ной симметричными горизонталями, ра-

вен /: Н.^

§ 59. Зависимость между углами на

местности и на снимке

Найдем значение угла на местно-

сти, соответствующее углу <р на снимке у--а,

(см. рис. 126).

АГ Рис. 128

Подставив сюда значения с1Х и йУ, полученные в предыдущем

параграфе, получим

} соз а

+ (х ф — у) зш а„

(9.41)

Рассмотрим частные случаи.

1. Снимок горизонтальный (а

= 0). В этом случае

т. е. на горизонтальном снимке равнинной местности нет угловых

искажений.

2. Вершина угла на снимке в точке нулевых искажений (х = 0,

у = /—а

/2). Подставив эти координаты в формулу (9.41), найдем

1§г|) = 1§ф.

Угол в точке нулевых искажений равен соответствующему углу

на равнинной местности.

3. Вершина угла ф в главной точке снимка (х = 0, у = 0).

В этом случае формула (9.41) принимает вид

= (§ф/соза

. (9.42)

4. Вершина угла ф в точке надира {х = 0, у = — / а

). После

подстановки этих значений х и у в формулу (9.41) получим

1§1|з = соза

1§ф. (9.43)

Найдем разность углов ср и яр, называемую угловым иска-

жением,

— Ф

(Ф — Ф) =

1 +1§

Ф 1§

155

Подставим сюда значение 1)5 из уравнения (9.41). Тогда

(х{ё

ш —

и) зт а„

—

2/ зт

/2]

(

— яр) = - - — {§ ф. (9.44)

(х

1§Ч> —

у) зт а

+ / (

°з

о + ф)

Отсюда следует, что угловое искажение равно нулю в следую-

щих случаях:

1. а

= 0; ф, х, у произвольны.

2. ф = 0; а

, /, х, у произвольны.

3. х = 0; у = —/а

/2, а

, Д ф произвольны.

4. х = 0; ф = 90°, а

, у произвольны.

5. ф = агс{§ У / ^ —. д ^ ^ произвольны.

Значение угла ср в пятом случае получается, если принять чис-

литель в равенстве (9.44) равным нулю и решить полученное таким

образом уравнение. Это значение ср соответствует направлению,

проходящему из данной точки через точку нулевых искажений.

На рис. 129 представлен снимок, в различных точках которого

построены индикатрисы угловых искажений (а

= 30°, / = 200 мм,

размер снимка 24 X 18 см). Искажение направления в какой-либо

точке снимка, например в точке 5, определяет отрезок, заключен-

ный между пересечениями этого направления с окружностью и ин-

дикатрисой.

Если начало координат на снимке перенести из главной точки

в точку нулевых искажений, сохранив направления осей хну,

то формула (9.44) примет вид

—

(ф _ г|>) = — - ф, (9.45)

где /' = //зт а

Найдем наибольшую разность <р—г|). Для этого дифференцируем

выражение (9.45)

(2х1

бФ

-у) (х *

ф-у + Г + Г *§

Ф)-

д (ф —

тр)

—(х + 2Г ф) (X 1§

ф —у ф)

(НеФ 1хЧу-у + Г (1 + ^

Ф)]

Пусть то значение ф, при котором ф—гр — экстремум, будет ф

Тогда

(2х

12 Фо

У)

Фо

+ /' + Г 1ё

Фо)

+ 2Г

18 Фо)

X (х1б

Фо

—

У*§Фо) = 0.

После перемножения получим

(х

+ ГУ) *ё

Фо

(1'х - ху)

Фо

+ Г

= 0.

Отсюда

- (Гх - ху) ± У(7'х - ху)

+ ГУ (X

+ ГУ)

*б Фо

= 7—7, • (9-46)

+ Г У

156

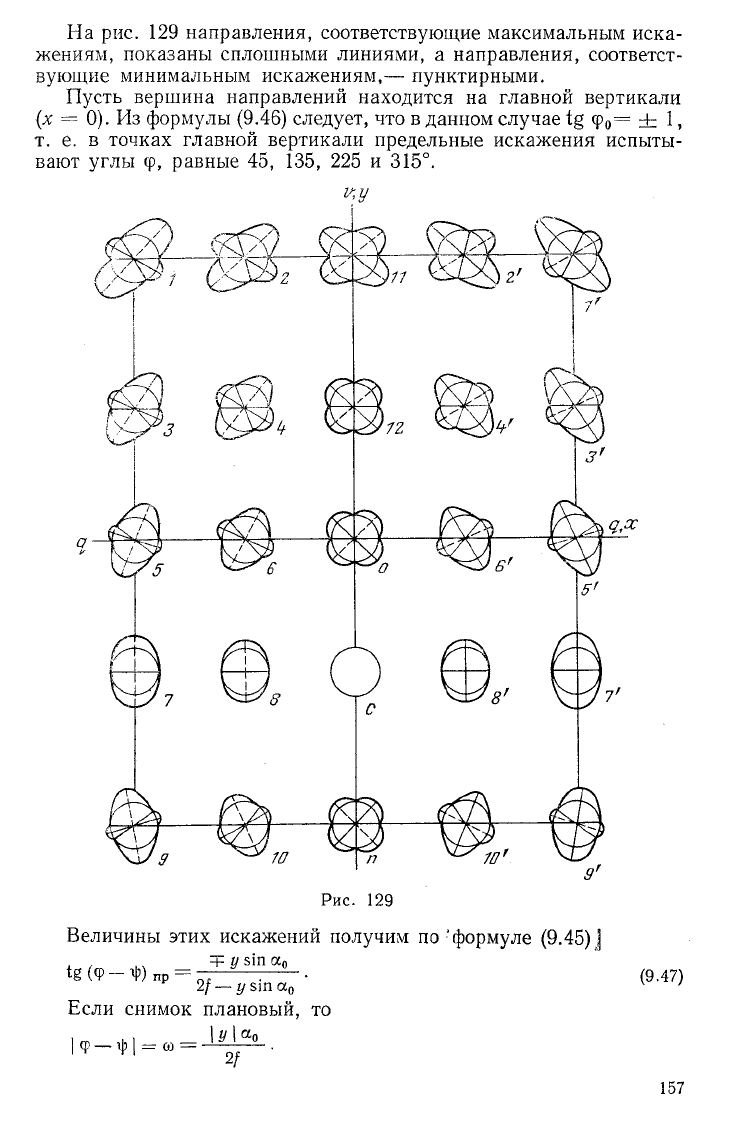
На рис. 129 направления, соответствующие максимальным иска-

жениям, показаны сплошными линиями, а направления, соответст-

вующие минимальным искажениям,— пунктирными.

Пусть вершина направлений находится на главной вертикали

(х = 0). Из формулы (9.46) следует, что в данном случае ф

= ± 1,

т. е. в точках главной вертикали предельные искажения испыты-

вают углы ф, равные 45, 135, 225 и 315°.

о,х

Рис. 129

Величины этих искажений получим по-формуле (9.45)]

+ и зш а„

(ф-ф) пр=

—

51П

Если снимок плановый, то

!«/!«о

Ф — гр ]

ш =

(9.47)

157

Если вершина направлений лежит на горизонтали, проходящей

через точку нулевых искажений (у = 0), т. е. на линии неискажен-

ных масштабов, то уравнение (9.46) принимает вид

<р

= ~2}'!х (9.48>

и вместо (9.45) для планового снимка получим

IФ 'ФI

пр

•

а„.

(9.49)

Из формул (9.48) и (9.49) следует, что в точках 1 (х = г, у — 0)

2 (х = 0, у = 2г) предельные угловые искажения ю одинаковы

(рис. 130). Такие же искажения имеют точки Г

(— г, 0) и 2' (0, — 2г).

Кривая равных предельных угловых ис-

кажений ю представляет собой две симме-

тричные параболы, пересекающиеся на

главной вертикали ою. Фокусы парабол сов-

падают с точкой нулевых искажений с. Рас-

стояния от точки с до вершин парабол равны

г, а расстояния до точек пересечения парабол

с главной вертикалью равны 2г [2].

Если предельное угловое искажение за-

дано, то

/• = /( со/а,,). (9.50)

Симметричные параболы ограничивают

Рис. 130 на плановом снимке зону предельных уг-

ловых искажений.

Положение главной вертикали и точки нулевых искажений на

плановом снимке, как правило, неизвестно. Поэтому вместо пара-

бол используют окружность с центром в главной точке о и радиу-

сом г' ж г.

В любой точке снимка, не выходящей за пределы, обозначенные

этой окружностью, угловые искажения не превышают заданного

значения со. Пусть со = 6', а

= 2,5°. Тогда согласно уравнению

(9.50)

/- = //25. (9.51)

§ 60. Смещения точек снимка, вызванные его наклоном

Пусть наклонный и горизонтальный снимки имеют общий центр

проекции 5 (рис. 131). В этом случае снимки пересекаются по го-

ризонтали Н

. проходящей через точку нулевых искажений с,

так как прямая 5с представляет собой биссектрису угла наклона

снимка а

и фокусные расстояния снимков Р и Р° одинаковы.

Обозначим через шит

изображения точки местности н:.! на-

клонном и горизонтальном снимках. Проведем радиус-векторы г

и г° от точки с к точкам т и т°. Углы, составленные г и г° с линией

, одинаковы, как показано в предыдущем параграфе. Поэтому

158

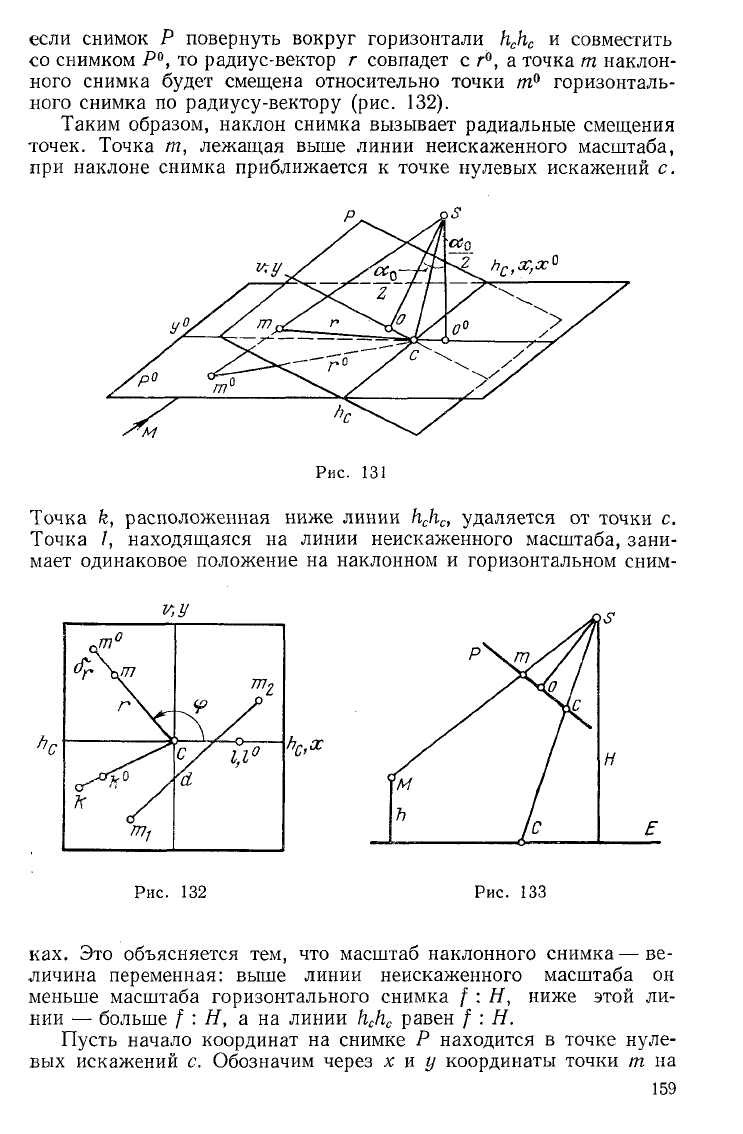
если снимок Р повернуть вокруг горизонтали Н

и совместить

со снимком Р°, то радиус-вектор г совпадет с г°, а точка т наклон-

ного снимка будет смещена относительно точки т° горизонталь-

ного снимка по радиусу-вектору (рис. 132).

Таким образом, наклон снимка вызывает радиальные смещения

точек. Точка т, лежащая выше линии неискаженного масштаба,

при наклоне снимка приближается к точке нулевых искажений с.

Рис. 131

Точка к, расположенная ниже линии Н

, удаляется от точки с.

Точка /, находящаяся на линии неискаженного масштаба, зани-

мает одинаковое положение на наклонном и горизонтальном сним-

ЪУ

<0°

дг

^р у

су

* с/

С/ 1

)Ъ

,аг

Рис. 132 Рис. 133

ках. Это объясняется тем, что масштаб наклонного снимка—ве-

личина переменная: выше линии неискаженного масштаба он

меньше масштаба горизонтального снимка I : Я, ниже этой ли-

нии — больше / : Я, а на линии Н

равен / : Я.

Пусть начало координат на снимке Р находится в точке нуле-

вых искажений с. Обозначим через х и у координаты точки т на

159