Lin S.D. Water and Wastewater Calculations Manual

Подождите немного. Документ загружается.

The porosity may range from a small fraction to about 0.90. Typical

values of porosity are 0.2 to 0.4 for sands and gravels depending on the

grain size, size of distribution, and the degree of compaction; 0.1 to 0.2

for sandstone; and 0.01 to 0.1 for shale and limestone depending on the

texture and size of the fissures (Hammer, 1986).

When groundwater withdraws from an aquifer and the water table is

lowered, some water is still retained in the voids. This is called the spe-

cific retention. The quantity drained out is called the specific yield. The

specific yield for alluvial sand and gravel is of the order of 90% to 95%.

Example: If the porosity of sands and gravels in an aquifer is 0.38 and the

specific yield is 92%, how much water can be drained per cubic meter of

aquifer?

solution:

Volume ⫽ 0.38 ⫻ 0.92 ⫻ 1 m

⫽ 0.35 m

2.2 Storativity

The term storativity (S) is the quantity of water that an aquifer will

release from storage or take into storage per unit of its surface area per

unit change in land. In unconfined aquifers, the storativity is in prac-

tice equal to the specific yield. For confined aquifers, storability is

between 0.005 and 0.00005, with leaky confined aquifers falling in the

high end of this range (US EPA, 1994). The smaller storativity of con-

fined aquifers, the larger the pressure change throughout a wide area

to obtain a sufficient supply from a well. However, this is not the case

for unconfined aquifers due to gravity drainage.

2.3 Transmissivity

Transmissivity describes the capacity of an aquifer to transmit a water.

It is the product of hydraulic conductivity (permeability) and the

aquifer’s saturated thickness:

T ⫽ Kb (3.5)

where T ⫽ transmissivity of an aquifer, gpd/ft or m

/(d ⭈ m)

K ⫽ permeability, gpd/ft

or m

/(d ⭈ m

)

b ⫽ thickness of aquifer, ft or m

A rough estimation of T is by multiplying specific capacity by 2000 (US

EPA, 1994).

Groundwater 185

Example: If the aquifer’s thickness is 50 ft, estimate the permeability of the

aquifer using data in the example of the specific capacity (in Section 2.7).

solution:

T ⫽ 2000 ⫻ specific capacity ⫽ 2000 ⫻ 15 gpm/ft

⫽ 30,000 gpm/ft

Rearranging Eq. (3.5)

K ⫽ T/b ⫽ (30,000 gpm/ft)/50 ft

⫽ 600 gpm/ft

2.4 Flow nets

Many groundwater systems are two or three dimensional. Darcy’s law

was first derived in a one dimensional equation. Using Darcy’s law can

establish a set of streamlines and equipotential lines to develop a two

dimensional flow net. The details of this concept are discussed else-

where in the text (Bedient et al., 1994).

A flow net is constructed by flow lines that intersect the equipoten-

tial lines or contour lines at a right angle. Equipotential lines are devel-

oped based on the observed water levels in wells penetrating an isotropic

aquifer. Flow lines are then drawn orthogonally to indicate the flow

direction.

Referring to Fig. 3.3, the horizontal flow within a segment in a flow

net can be determined by the following equation (US EPA, 1994):

⫽ T

⌬H

(3.6)

186 Chapter 3

Figure 3.3 Distribution of transmissivity in flow nets.

where q

⫽ groundwater flow in segment A, m

/d or ft

⫽ transmissivity in segment A, m

/d or ft

⌬H

⫽ drop in groundwater level across segment A, m or ft

⫽ average width of segment A, m or ft

⫽ average length of segment A, m or ft

The flow in the next segment, B, is similarly computed as Eq. (3.7)

⫽ T

⌬H

(3.7)

Assuming that there is no flow added between segments A and B by

recharge (or that recharge is insignificant), then

⫽ q

or T

⌬H

⫽ T

⌬H

solving T

computation of which allows T

from T

⫽ T

⌬H

) (3.8)

Measurement or estimation of transmissivity (T ) for one segment

allows the computation of variations in T upgradient and downgradi-

ent. If variations in aquifer thickness are known, or can be estimated

for different segments, variation in hydraulic conductivity can also be

calculated as

K ⫽ T/b (3.9)

where K ⫽ hydraulic conductivity, m/d or ft/d

T ⫽ transmissivity, m

/d or ft

b ⫽ aquifer thickness, m or ft

Equation (3.9) is essentially the same as Eq. (3.5).

2.5 Darcy’s law

The flow movement of water through the ground is entirely different

from the flow in pipes and in an open channel. The flow of fluids through

porous materials is governed by Darcy’s law. It states that the flow

velocity of fluid through a porous medium is proportional to the

hydraulic gradient (referring to Fig. 3.4):

v ⫽ Ki (3.10a)

(3.10b)v 5 K

1 z

d 2 sh

1 z

Groundwater 187

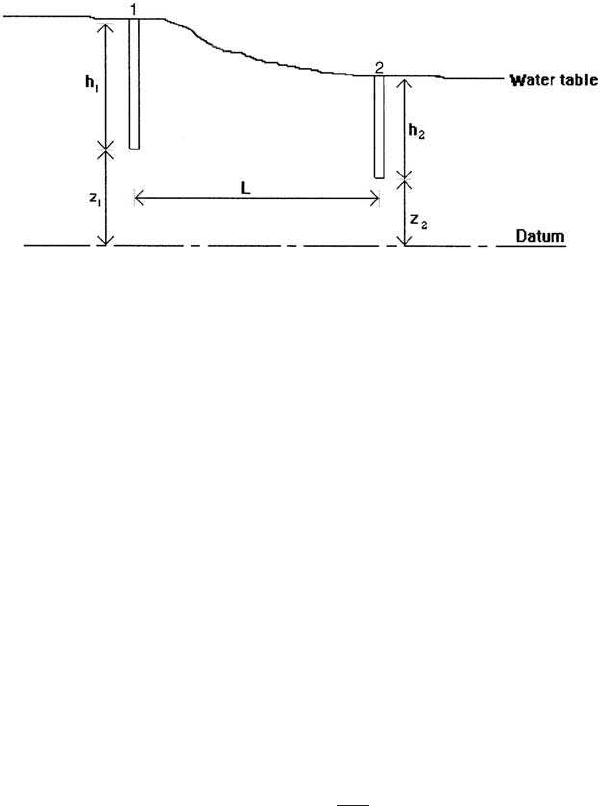
where v ⫽ Darcy velocity of flow, mm/s or ft/s

K ⫽ hydraulic conductivity of medium or coefficient of

permeability, mm/s or ft/s

i ⫽ hydraulic gradient, mm or ft/ft

, h

⫽ pressure heads at points 1 and 2, m or ft

, z

⫽ elevation heads at points 1 and 2, m or ft

L ⫽ distance between points (piezometers) 1 and 2,

m or ft

The pore velocity v

is equal to the Darcy velocity divided by porosity as

follows:

⫽ v/n (3.11)

Darcy’s law is applied only in the laminar flow region. Groundwater

flow may be considered as laminar when the Reynolds number is less

than unity (Rose, 1949). The Reynolds number can be expressed as

(3.12)

where R ⫽ Reynolds number

V ⫽ velocity, m/s or ft/s

D ⫽ mean grain diameter, mm or in

␯⫽kinematic viscosity, m

/d or ft

Example 1: Determine the Reynolds number when the groundwater tem-

perature is 10⬚C (from Table 4.1a, ␯⫽ 1.31 ⫻ 10

⫺6

/s); the velocity of flow

is 0.6 m/d (2 ft/d); and the mean grain diameter is 2.0 mm (0.079 in).

R 5

188 Chapter 3

Figure 3.4 Groundwater flow (one dimensional).

solution:

V ⫽ 0.6 m/d ⫽ (0.6 m/d)/(86,400 s/d)

⫽ 6.94 ⫻ 10

–6

m/s

D ⫽ 2 mm ⫽ 0.002 m

⫽ 0.011

Note: It is a laminar flow (R ⬍ 1).

Example 2: If the mean grain diameter is 0.12 in (3.0 mm), its porosity is

40%, and the groundwater temperature is 50⬚F (10⬚C). Determine the

Reynolds number for a flow 5 ft (1.52 m) from the centerline of the well with

a 4400 gpm in a confined aquifer depth of 3.3 ft (1 m) thick.

solution:

Step 1. Find flow velocity (V )

Q ⫽ 4400 gpm ⫻ 0.002228 cfs/gpm

Q ⫽ 9.80 cfs

n ⫽ 0.4

r ⫽ 5 ft

h ⫽ 3.3 ft

Since Q ⫽ nAV ⫽ n(2␲rh)V

V ⫽ Q/n(2␲ rh)

⫽ 9.8 cfs/(0.4 ⫻ 2 ⫻ 3.14 ⫻ 5 ft ⫻ 3.3 ft)

⫽ 0.236 fps

Step 2. Compute R

␯⫽1.41 ⫻ 10

–5

/s (see Table 4.1b at 50⬚F)

D ⫽ 0.12 in ⫽ 0.12 in/(12 in/ft) ⫽ 0.01 ft

⫽ 167

Example 3: The slope of a groundwater table is 3.6 m per 1000 m. The coef-

ficient of permeability of coarse sand is 0.51 cm/s (0.2 in/s). Estimate the flow

velocity and the discharge rate through this aquifer of coarse sand 430 m

(1410 ft) wide and 22 m (72 ft) thick.

R 5

0.236 fps 3 0.01 ft

1.41 3 10

R 5

6.94 3 10

m/s 3 0.002 m

1.31 3 10

Groundwater 189

solution:

Step 1. Determine the velocity of flow, v, using Eq. (3.10a)

i ⫽ 3.6 m/1000 m ⫽ 0.0036

v ⫽ Ki ⫽ 0.51 cm/s(0.0036)

⫽ 0.00184 cm/s (86,400 s/d)(0.01 m/cm)

⫽ 1.59 m/d

⫽ 5.21 ft/d

Step 2. Compute discharge

Q ⫽ ␯A ⫽ 1.59 m/d ⫻ 430 m ⫻ 22 m

⫽ 15,040 m

/d ⫻ 264.17 gal/m

⫽ 3.97 MGD (million gallons per day)

Example 4: The difference in water level between two wells 1.6 miles

(2.57 km) apart is 36 ft (11 m), and the hydraulic conductivity of the media

is 400 gpd/ft

(16,300 L/(d ⭈ m

)). The depth of the media (aquifer) is 39 ft

(12 m). Estimate the quantity of groundwater flow moving through the cross

section of the aquifer.

solution:

i ⫽ 36 ft/1.6 miles ⫽ 36 ft/(1.6 miles ⫻ 5280 ft/miles)

⫽ 0.00426

A ⫽ 1.6 ⫻ 5280 ft ⫻ 39 ft

⫽ 329,500 ft

then Q ⫽ KiA ⫽ 400 gpd/ft

⫻ 0.00426 ⫻ 329,500 ft

⫽ 561,400 gpd

⫽ 0.561 MGD

⫽ 2,123 m

Example 5: If the water moves from the upper to the lower lake through the

ground. The following data are given:

difference in elevation ⌬h ⫽ 25 m (82 ft)

length of low path L ⫽ 1500 m (4920 ft)

cross-sectional area of flow A ⫽ 120 m

(1290 ft

)

hydraulic conductivity K ⫽ 0.15 cm/s

porosity of media n ⫽ 0.25

Estimate the time flow between the two lakes.

190 Chapter 3

solution:

Step 1. Determine the Darcy velocity v

v ⫽ Ki ⫽ K⌬h/L ⫽ 0.0015 m/s (25 m/1500 m)

⫽ 2.5 ⫻ 10

–5

m/s

Step 2. Calculate pore velocity

⫽ v/n ⫽ (2.5 ⫻ 10

–5

m/s)/0.25

⫽ 1.0 ⫻ 10

–4

m/s

Step 3. Compute the time of travel t

t ⫽ L/v

⫽ 1500 m/(1 ⫻ 10

–4

m/s)

⫽ 1.5 ⫻ 10

s ⫻ (1 day/86,400 s)

⫽ 173.6 days

2.6 Permeability

The terms permeability (P) and hydraulic conductivity (K ) are often used

interchangeably. Both are measurements of water moving through the

soil or an aquifer under saturated conditions. The hydraulic conductiv-

ity, defined by Nielsen (1991), is the quantity of water that will flow

through a unit cross-sectional area of a porous media per unit of time

under a hydraulic gradient of 1.0 (measured at right angles to the direc-

tion of flow) at a specified temperature.

Laboratory measurement of permeability. Permeability can be determined

using permeameters in the laboratory. Rearranging Eq. (3.5) and Q ⫽

vA, for constant head permeameter, the permeability is

(3.13)

where K ⫽ permeability, m/d or ft/d

L ⫽ height of sample (media), m or ft

Q ⫽ flow rate at outlet, m

/d or ft

H ⫽ head loss, m or ft

R ⫽ radius of sample column

The permeability measure from the falling-head permeameter is

(3.14)K 5 a

ln a

K 5

HpR

Groundwater 191

where r ⫽ radius of standpipe, m or ft

⫽ height of water column at beginning, m or ft

⫽ height of the water column at the end, m or ft

t ⫽ time interval between beginning and end, day

Other parameters are the same as Eq. (3.13).

Groundwater flows through permeable materials, such as sand,

gravel, and sandstone, and is blocked by less permeable material, such

as clay. Few materials are completely impermeable in nature. Even

solid bedrock has fine cracks, so groundwater can flow through.

Groundwater recharge occurs when surface water infiltrates the soil

faster than it is evaporated, used by plants, or stored as soil moisture.

Field measurement of permeability. Ideal steady-state flow of ground-

water is under the conditions of uniform pump withdrawal, a stable

drawdown curve, laminar and horizontal uniform flow, a flow velocity

proportional to the tangent of the hydraulic gradient, and a homoge-

neous aquifer. Assuming these ideal conditions, the well flow is a func-

tion of the coefficient of permeability, the shape of the drawdown curve,

and the thickness of the aquifer. For an unconfined aquifer the well

discharge can be expressed as an equilibrium equation (Steel and

McGhee, 1979; Hammer and Mackichan, 1981):

(3.15)

where Q ⫽ well discharge, L/s or gpm

␲ ⫽ 3.14

K ⫽ coefficient of permeability, mm/s or fps

H ⫽ saturated thickness of aquifer before pumping, m or ft

(see Fig. 3.1)

⫽ depth of water in the well while pumping, m or ft

⫽ h ⫹ well losses in Fig. 3.1

r ⫽ radius of influence, m or ft

⫽ radius of well, m or ft

Also under ideal conditions, the well discharge from a confined aquifer

can be calculated as

(3.16)

where m is the thickness of the aquifer, m or ft. Other parameters are

the same as Eq. (3.15). Values of Q, H, and r may be assumed or meas-

ured from field well tests, with two observation wells, often establishing

Q 5 2pKm

H 2 h

ln sr/r

Q 5 pK

2 h

ln sr/r

192 Chapter 3

a steady-state condition for continuous pumping for a long period. The

coefficient of permeability can be calculated by rearranging Eqs. (3.14)

and (3.15). The K value of an unconfined aquifer is also computed by the

equation:

(3.17)

and for a confined aquifer:

(3.18)

where h

, h

⫽ depth of water in observation wells 1 and 2, m or ft

, r

⫽ centerline distance from the well and observation

wells 1 and 2, respectively, m or ft

Example 1: A well is pumped to equilibrium at 4600 gpm (0.29 m

/s) in an

unconfined aquifer. The drawdown in the observation well at 100 ft (30.5 m)

away from the pumped well is 10.5 ft (3.2 m) and at 500 ft (152 m) away is

2.8 ft (0.85 m). The water table is 50.5 ft (15.4 m). Determine the coefficient

of permeability.

solution:

⫽ 50.5 ft – 10.5 ft ⫽ 40.0 ft

⫽ 50.5 ft – 2.8 ft ⫽ 47.7 ft

⫽ 100 ft

⫽ 500 ft

Q ⫽ 4600 gpm ⫽ 4600 gmp ⫻ 0.002228 cfs/gpm

⫽ 10.25 cfs

Using Eq. (3.17)

⫽ 0.00778 ft/s

or ⫽ 0.00237 m/s

Example 2: Referring to Fig. 3.1, a well with a diameter of 0.46 m (1.5 ft) is

in a confined aquifer which has a uniform thickness of 16.5 m (54.1 ft). The

s10.25 cfsd ln s500 ft/100 ftd

3.14[s47.7 ftd

2 s40 ftd

]

K 5

Qlnsr

psh

2 h

K 5

Q ln sr

2mpsh

2 h

K 5

Q ln sr

psh

2 h

Groundwater 193

depth of the top impermeable bed to the ground surface is 45.7 m (150 ft). Field

pumping tests are carried out with two observation wells to determine the

coefficient of permeability of the aquifer. The distances between the test well

and observation wells 1 and 2 are 10.0 and 30.2 m (32.8 and 99.0 ft), respec-

tively. Before pumping, the initial piezometric surface in the test well and the

observation wells are 10.4 m (34.1 ft) below the ground surface. After pump-

ing at a discharge rate of 0.29 m

/s (4600 gpm) for a few days, the water

levels in the wells are stabilized with the following drawdowns: 8.6 m

(28.2 ft) in the test well, 5.5 m (18.0 ft) in the observation well 1, and 3.2 m

(10.5 ft) in the observation well 2. Compute (a) the coefficient of permeabil-

ity and transmissivity of the aquifer and (b) the well discharge with the draw-

down in the well 10 m (32.8 ft) above the impermeable bed if the radius of

influence (r) is 246 m (807 ft) and ignoring head losses.

solution:

Step 1. Find K

Let a datum be the top of the aquifer, then

H ⫽ 45.7 m – 10.4 m ⫽ 35.3 m

⫽ H – 8.6 m ⫽ 35.3 m – 8.6 m ⫽ 26.7 m

⫽ 35.3 m – 5.5 m ⫽ 29.8 m

⫽ 35.3 m – 3.2 m ⫽ 32.1 m

m ⫽ 16.5 m

Using Eq. (3.18)

⫽ 0.00134 m/s ⫽ 115.8 m/d

or ⫽ 0.00441 ft/s

Step 2. Find T using Eq. (3.5)

T ⫽ Kb ⫽ 115.8 m/d ⫻ 16.5 m

⫽ 1910 m

Step 3. Estimate well discharge

⫽ 10 m, r

⫽ 0.46 m

H ⫽ 35.3 m, r ⫽ 246 m

0.29 m

/s ln s30.2 m/10 md

2 3 3.14 3 16.5 m 3 s32.1 m 2 29.8 md

K 5

Q ln sr

2pmsh

2 h

194 Chapter 3