Левшунов В.М Инженерные конструкции
Подождите немного. Документ загружается.

111
.
;
;Н)НН(
;
НLL
)
L
Н
LLLL
(
;
Н
)ННН(
;LН
РВРВРВ
РВРПРПРП
РВ
РПРПРПРП
РВ
РВРВРВ
РПРВ
0
0
1
2
1
2
2122223
2
222
1
2
3
2
3
2
2
1
2
2
3223
3113
2
2112
23
33
3
22
11
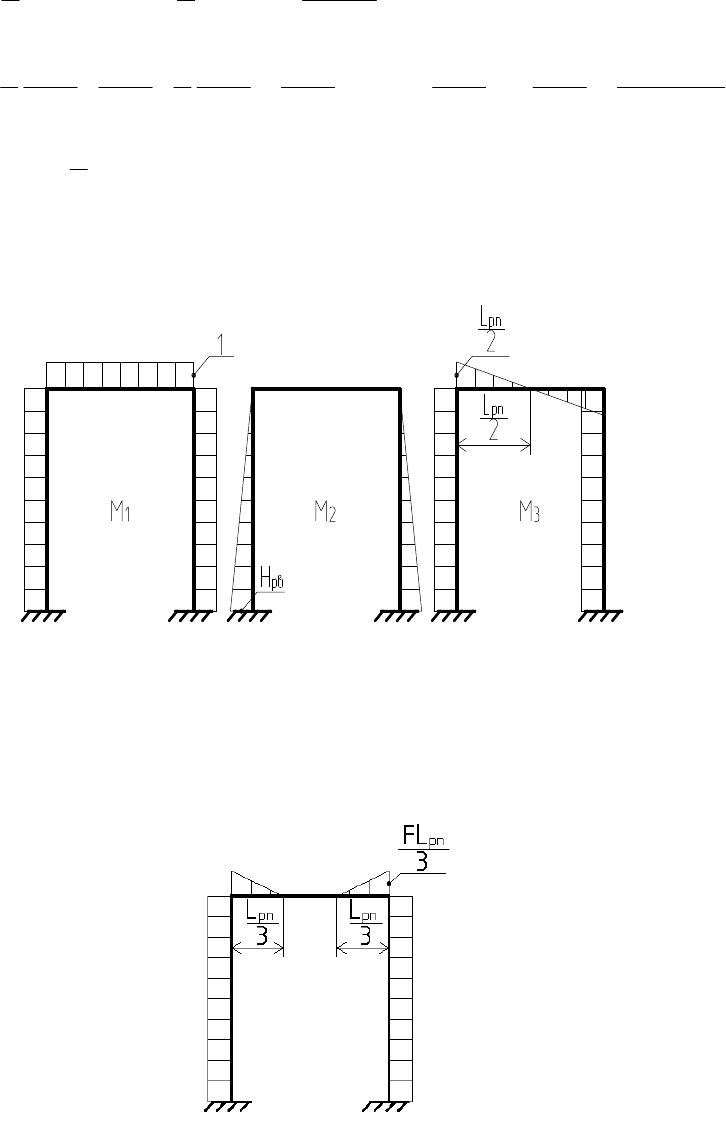
Рис. 36. Расчетные схемы единичных эпюр изгибающих моментов
3. Грузовая эпюра изгибающих моментов для основной системы
метода сил (рис. 37).
Рис. 37. Расчетная схема грузовой эпюры изгибающих моментов
4. Грузовые перемещения точек приложения лишних неизвест-
ных по линии действия силовой сосредоточенной нагрузки:

112
3
2
9
2
3
3
3
2
1
2
1
РВРПРП
РВ
РПРПРП
F
НLFL
)Н
LLFL
(
;
3
2
3
2
1
2
2
2
РВРПРП
РВF
НFL
)
FL
H(
;
0
3
F
.
5. Система трех канонических уравнений метода сил с тремя не-
известными и ее решение:
.Х)
НLL
(
;
НFL
Х
Н
ХН
;)
НFLFL
(ХНХ)LН(
РВРПРП
РВРПРВ
РВ
РВРПРП
РВРПРВ
0
2
12
0
33
2
0
3
2
9
2
3
23
2
2
3
1
2
2
2
2
1
Из третьего уравнения следует, что Х
3
= 0. В результате имеем
систему двух канонических уравнений с двумя неизвестными:
.)НFLFL(ХНХ)LН(
;НFLХНХН
РВ
РП
РП
РВ
РП
РВ
РВРПРВРВ
06929
023
2
2
2
1
2
2
3
1
2
Умножаем первое уравнение на 9, а второе уравнение – на 2Н
РВ
,
получаем преобразованную систему двух канонических уравнений
метода сил с двумя неизвестными:
.)НFLFL(НХНХ)LН(Н
;НFLХНХН
РВ
РП
РП
РВ
РВ
РП
РВ
РВ
РВРПРВРВ
06218218
091827
2
2
3
1
2
2
3
1
2
Из первого уравнения вычитаем второе уравнение и получаем
уравнение следующего вида:
,)]НFL
FL(ННFL[Х)LН(НХН
РВ
РП
РПРВРВРПРПРВРВРВ
06
2921827
22
11
2
из которого следует, что Х
1
определяется по расчетной зависимости
)НL(
)НL(FL
LН
FLНFL
Х
РВРП
РВРПРП
РПРВ
РПРВРП
2
32
9189
23
2
1
.
Выражение для Х
1
подставляем в первое преобразованное кано-
ническое уравнение и получаем:
02
2
32
9
3
2
РПРВ
РВРП
РВРПРП
FLХН
)НL(
)НL(FL
, откуда расчетная зави-
симость для Х
2
имеет следующее выражение:
113
.
)НL(
Н
FL
)НL(Н
FL
)НL(Н
)НL(FL)НL(FL
Х
РВ
РП
РВ
РП
РВРПРВ
РП
РВРПРВ
РВРПРПРВ
РП
РП
2
1
3
2
232
4
232
2332
2
2
2
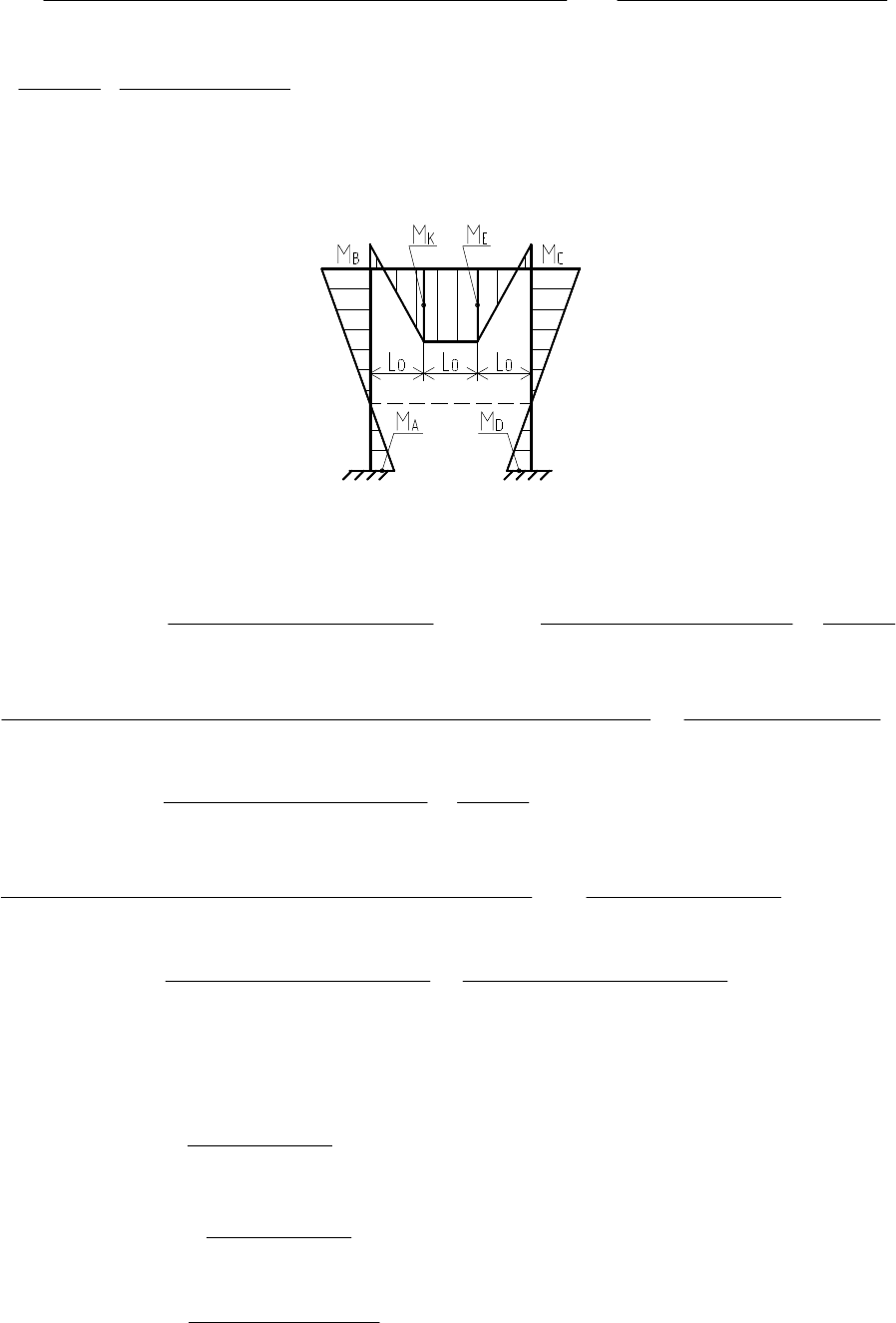
6. Ординаты эпюры изгибающих моментов в узловых точках ос-
новной системы метода сил (рис. 38).
Рис. 38. Расчетная схема эпюры изгибающих моментов
.
)НL(
FL
)НL(
НFLFLFLНFLFL
FL
)НL(Н
FL
Н
)НL(
)НL(FL
ММ
РВРП
РП
РВРП
РВРПРПРПРВРПРП
РП
РВРПРВ
РП
РВ
РВРП
РВРПРП
DА
29
2
29
36632
323
2
29
32
1
2222
2
.
)НL(
FL
)НL(
НFLFLНFLFL
FL
)НL(
)НL(FL
ММ
РВРП
РП
РВРП
РВРПРПРВРПРП
РП
РВРП
РВРПРП
СВ
29
4
29
3632
329
32
1
222
.
)НL(
)НL(FL
)НL(
)НL(FL
ММ
РВ
РП
РВРПРП
РВ
РП
РВРПРП
ЕК
29
32
29
32
1
Введем относительную величину К = Н
РВ
/L
РП
, заменим L
РП
на 3L
O
и окончательно будем иметь:
.
)K(
)K.(FL
ММ
;
)К(L
FL
ММ
;
)К(L
FL
ММ
O
ЕК
РП
O
СВ
РП
O
DА
23
5112
2
4
2
2
2
2
114
Расчеты по расчетным формулам Д.В. Бычкова.
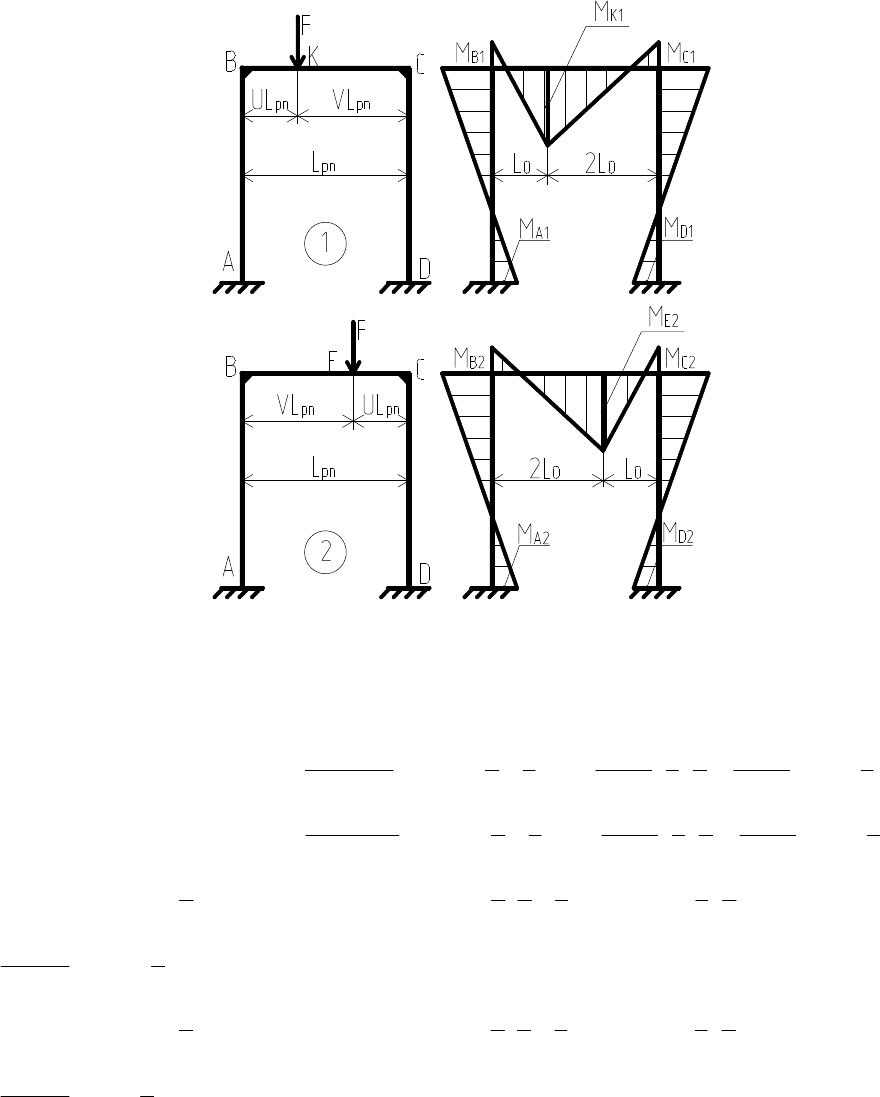
1. Ординаты эпюры изгибающих моментов в узловых точках ос-
новной системы рамы для симметричной сосредоточенной силовой
нагрузки (рис. 39).
Рис. 39. Расчетные схемы основной системы рамы
для симметричной сосредоточенной силовой нагрузки
].
6
1
[
9
2
3
2
3
1
])
3
1
3
2
(
2
1
[])(
2
1
[
].
6
1
1[
9
2
3
2
3
1
])
3
1
3
2
(
2
1
[])(
2
1
[
].
3
1
[
93
2
3
1
2
])
3
1
3
2
([
2
])([
].
3
1
[
93
2
3
1
2
])
3
1
3
2
([
2
])([
21
212112
21
212121
21212112
21212121
KK
FL
FLKKUVFLKUVKMM
KK
FL
FLKKUVFLKUVKMM
KK
FLFL
KK
UVFL
KUVKMM
KK
FLFL
KK
UVFL
KUVKMM
РП
РПРПCB
РП
РПРПCB
РПРПРП
DA
РПРПРП
DA
Примечание. Относительные величины К
1
= 1/(1+К) и К
2
= 1/(1+6К), где
К = Н
РВ
/L
РП.
115
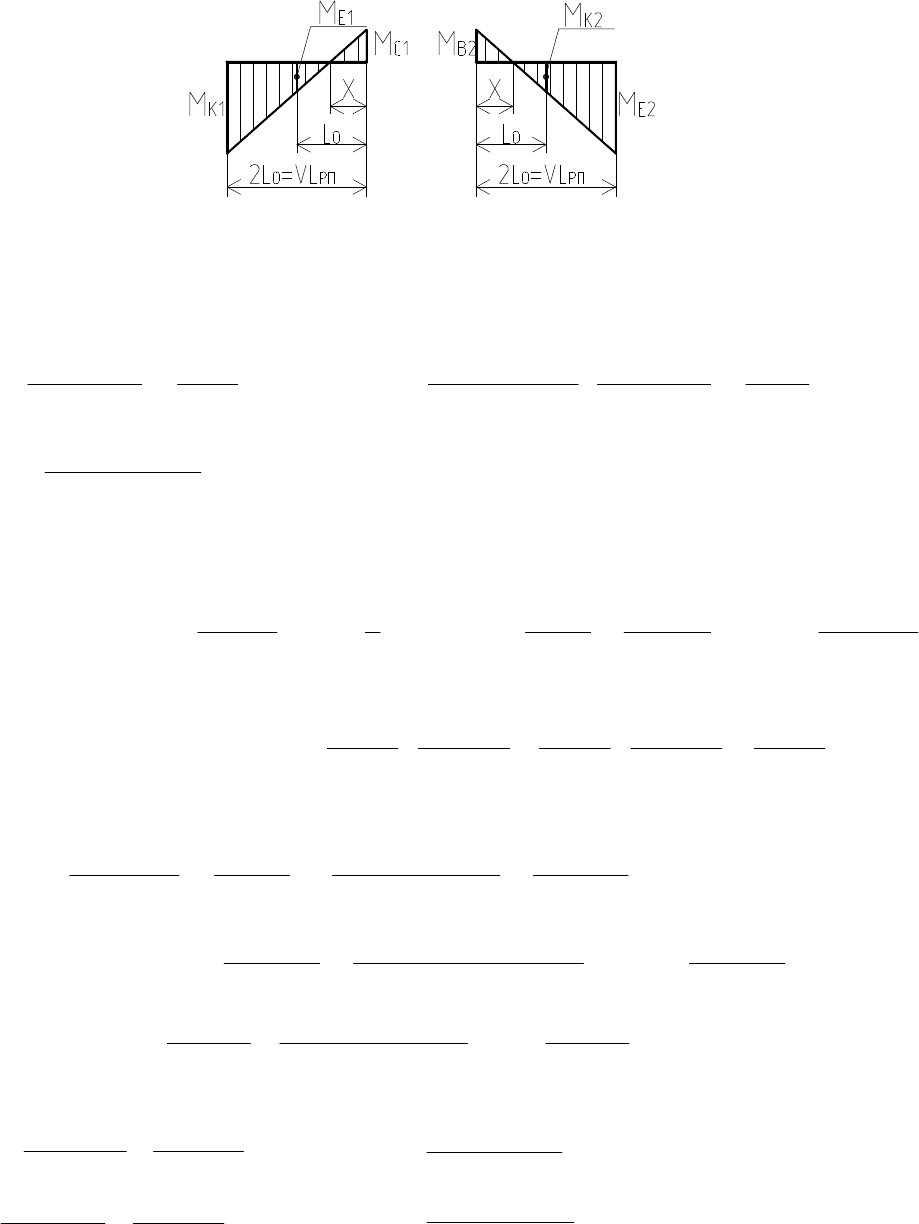
2. Соотношения подобия прямоугольных треугольников для по-
лучения расчетных формул Д.В. Бычкова ординат эпюры изгибающих
моментов и поперечных сил (рис. 40).
Рис. 40. Расчетные схемы подобия прямоугольных треугольников
1) Соотношения подобия прямоугольных треугольников первого
вида:
X
M
XL
M
C
O
K
1
1
2
, откуда ;
2
11
01
CK
C
MM
LM
X
X
M
XL
M
B
O
E 22
2
, отку-
да .
2
22
2
BE
OB
MM
LM
X
Выполняем преобразования выражений для Х.
В числителе:
.
)K(
FL
L]
)K(
[
FL
L]KK[
FL
LMLM
O
O
O
O
РП
OBOC
23
4
2
2
1
3
2
2
6
1
9
2
22
2
2121
В знаменателе:
.
3
2
)2(
1
3
2
)2(
)1(
3
2
)()(
2211
OOO
BECK
FL
K
FL
K
KFL
MMMM
После выполненных преобразований получаем:
;
)2(
2
)2(6
12
]
3
2
/[]
)2(3
4
[
22
K
L
KFL
FLFL
K
FL
X
O
O
OOO
;
)2(
)1(
2
)2(
2)2(2
)2(
2
22
K
K
L
K
LKL
K
L
LXL
O
OOO
OO
.
)2()2(
2)2(
)2(
2
K
K
L
K
LKL
K
L
LXL
O
OOO
OO
2) Соотношения подобия прямоугольных треугольников второго
вида:
)()2(
11
XL
M
XL
M
O
E
O
K
, откуда
;
)2(
)(
1
1
XL
XLM
M
O
OK
E
)()2(
22
XL
M
XL
M
O
K
O
E
, откуда
.
)2(
)(
2
2
XL
XLM
M
O
OE
K
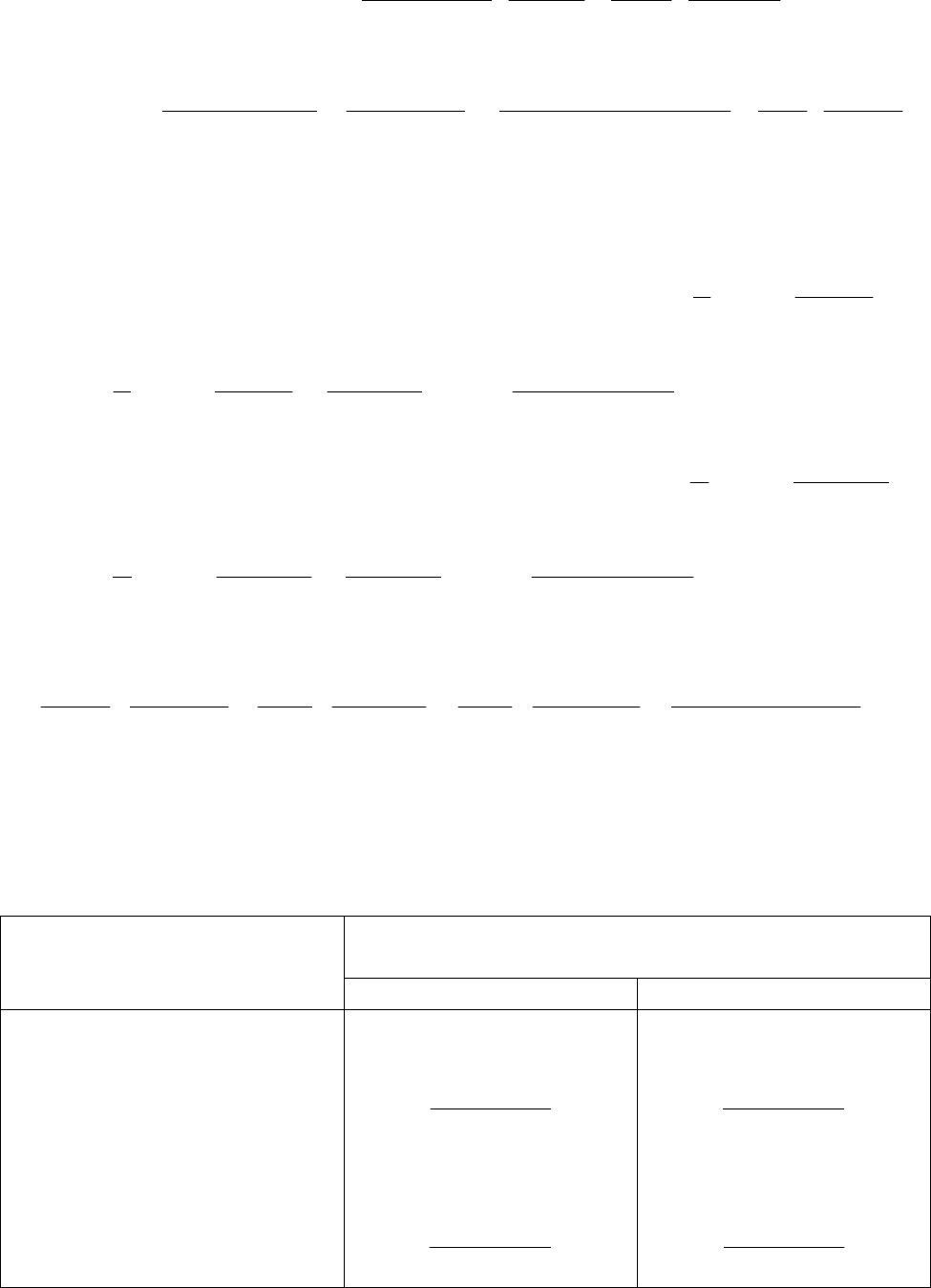
116
Выполняем преобразование выражений для М
Е1
= М
К2
:
2
2
21
)2(
)1(
3
2
)2()2(3
)1(2
)]([)]([
K
KK
FL
K
KL
K
KFL
XLMXLM
OOO
OEOK
и получаем:
.
)2(3
)1()2(3
)2)(1(2
]
)2(
)1(2
/[]
)2(3
)1(2
[
2
2
2
2
21
K
K
FL
KK
KKKFL
K
KL
K
KKFL
MM
OOOO
KE
3. Расчетные формулы Д.В. Бычкова для ординат эпюры изги-
бающих моментов и поперечных сил в узловых точках жесткой рамы
и в расчетных поперечных сечениях ригеля:
.
)K(L
FL
К
FLFL
]KK[
FL
]KK[)MM(M)MM(M
РП
О
РПРП
РП
DDDAAA
2
2
9
2
93
1
93
1
2
121
211221
.
)К(L
FL
К
FLFL
]KK[
FL
]KK[)MM(M)MM(M
РП
OРПРП
РП
CCCBBB
2
4
9
4
9
2
6
1
9
2
6
1
2
121
211221
.
)K(
)K.(FL
)K(
)K(
FL
)K(
K
FL
)K(
))K(
FL
)MM(M)MM(M
OOOO
EEEKKK
23
5112
2
32
3232
1
3
2
1221
Расчеты показывают, что ординаты эпюры изгибающих момен-
тов в узловых точках жесткой рамы и в расчетных поперечных сече-
ниях ригеля идентичны (табл. 1).
Таблица 1
Сводные результаты расчетов ординат эпюры изгибающих моментов
Расчетные выражения ординат эпюры расчетных
изгибающих моментов
Конструктивные элементы
рамы
Метод сил Расчетные формулы
1. Жесткие узлы вертикаль-
ных стоек:
узел А
узел D
2. Жесткие узлы вертикаль-
ных стоек и горизонтально-
го ригеля:
узел В
узел С
)2(
2
2
КL
FL
РП
O
)2(
4
2
КL
FL
РП
O
)2(
2
2
КL
FL
РП
O
)2(
4
2
КL
FL
РП
O
117
Окончание табл. 1
Расчетные выражения ординат эпюры расчетных
изгибающих моментов
Конструктивные элементы
рамы
Метод сил Расчетные формулы
3. Поперечные сечения го-
ризонтального ригеля:
сечение К
сечение Е
)2(3
)5.11(2
K
KFL
O
)2(3
)5.11(2
K
KFL
O
4. Расчетные формулы Д.В. Бычкова для ординат эпюры попе-
речных сил в узловых точках жесткой рамы (рис. 41).
Рис. 41. Расчетная схема ординат эпюры поперечных сил
Вертикальная стойка АВ:
.
)К(НL
FL
Н
]
)К(L
FL
)К(L
FL
[
H
MM
QQ
РВРП
O
РВРП
O
РП
O
PB
AB
C
B
C
A
2
6
1
2
2
2
4
0
222
Вертикальная стойка СD:
.
)К(L
FL
H
]
)К(L
FL
)К(L
FL
[
H
MM
QQ
РП
O
PBРП
O
РП
O
PB
CD
C
D
C
C
2
6
1
2
6
2
2
0
222
Горизонтальный ригель ВС:
.F
L
]
)К(L
FL
)К(L
FL
[F
L
MM
FQQ
РП
РП
O
РП
O
РП
BC
P
C
P
B
1
2
4
2
4
22
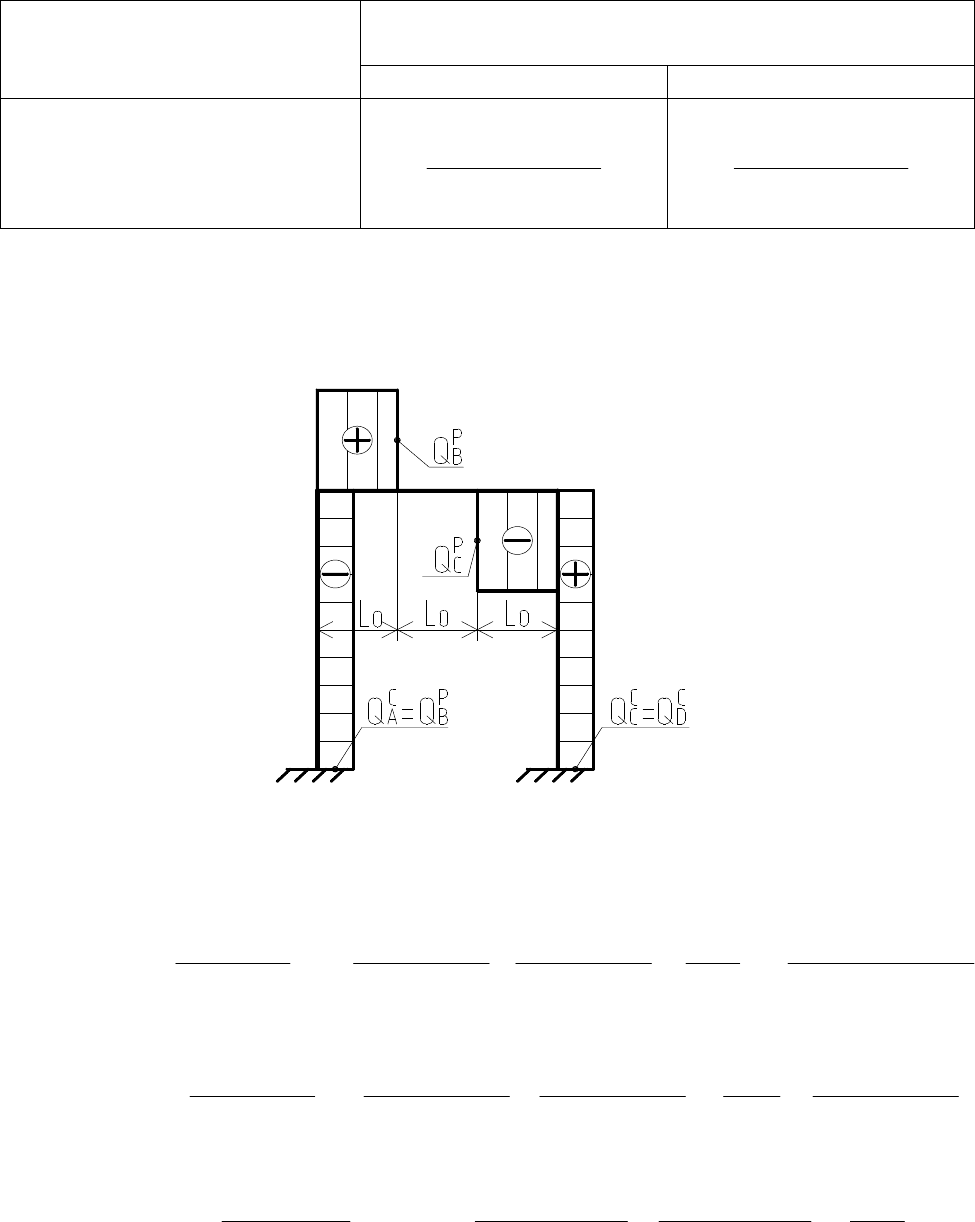
5. Расчетные формулы Д.В. Бычкова для ординат эпюры про-
дольных сил в поперечных сечениях жесткой рамы (рис. 42).
118
Рис. 42. Расчетная схема ординат эпюры продольных сил
Вертикальные стойки АВ и СD: .FNN
CDAB
Горизонтальный ригель ВС: .
)К(НL
FL
N
РВРП
O
BC
2
6
2
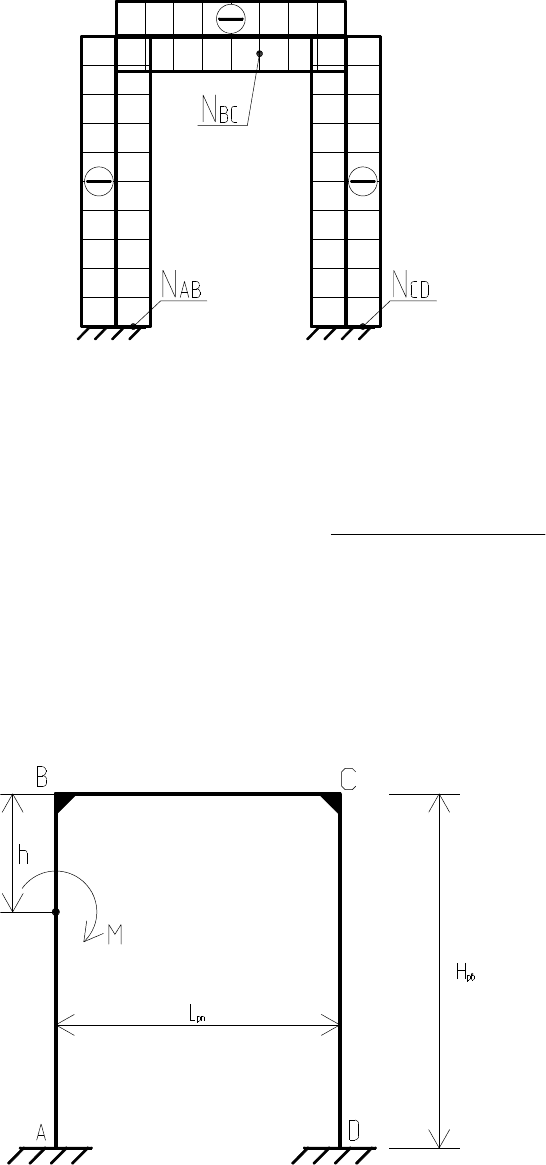
Пример 2. Установить ординаты эпюры изгибающих моментов в
узловых точках жесткой рамы П-образного вида, нагруженной сосре-
доточенной моментной нагрузкой на левую вертикальную стойку по-
стоянного сечения (рис. 43).
Рис. 43. Расчетная схема нагружения жесткой рамы
сосредоточенной моментной нагрузкой
Расчеты по методу сил.
1. Грузовая эпюра изгибающих моментов для основной системы
метода сил (рис. 44).
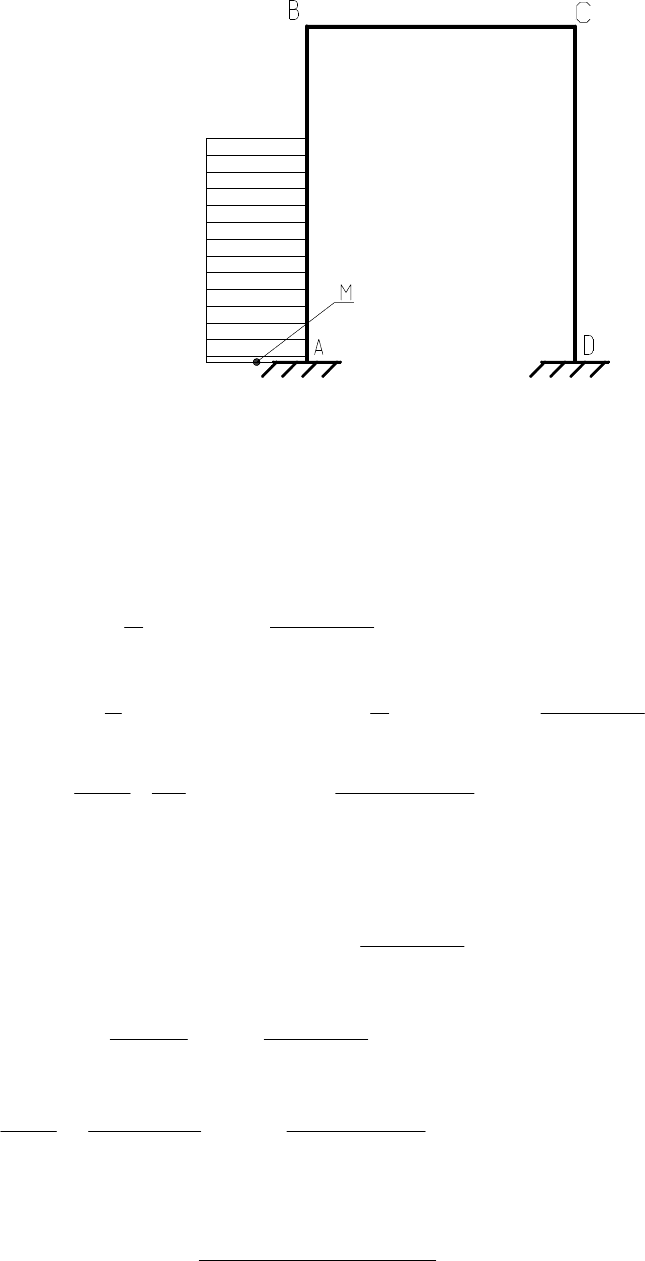
119
Рис. 44. Расчетная схема грузовой эпюры
изгибающих моментов
2. Грузовые перемещения точек приложения лишних неизвест-
ных по линии действия сосредоточенной моментной нагрузки:
;
МН
НМ
РВ
РВМ
3
2
1
3
2
1
;
MH
MH]/)HH[(
PB
PBPBPBМ
9
4
3
2
2
3
1
2
2
.
LМН
МН
L
РПРВ
РВ
РП
М
3
30
2
2
3
3. Система канонических трех уравнений метода сил с тремя не-
известными и ее решение:
.
LМН
Х)
НLL
(
;
МН
Х
Н
ХН
;
МН
ХНХ)LН(
РПРВРВРПРП
РВРВ
РВ
РВ
РВРПРВ
0
3
2
12
0
9
4
3
2
0
3
2
2
3
23
2
2
3
1
2
2
2
1
Из третьего уравнения 046
3
23
РПРВеРВРПРП
LМНХ)НLL(
следует, что .
)НL(L
МН
Х
РВРпРП
РВ
6
4
3
В результате имеем систему двух канонических уравнений мето-
да сил с двумя неизвестными:
120
.МНХНХН
;МНХНХ)LН(
РВ
РВ
РВ
РВРВРПРВ
2
2
3
1
2
2
2
1
469
02323
Умножаем первое уравнение на 2Н
РВ
и получаем преобразован-
ную систему двух канонических уравнений метода сил с двумя неиз-
вестными:
.МНХНХН
;МНХНХ)LН(Н
РВ
РВ
РВ
РВРВРПРВРВ
0469
04626
2
2
3
1
2
2
2
3
1
Из первого уравнения преобразованной системы канонических
уравнения метода сил вычитаем второе и получаем:
.X]Н)LH(H[
РВ
РП
PB
PB
0926
1
2
Откуда следует, что Х
1
= 0. То-
гда из второго уравнения получаем:
.Н
М
Н
МН
Х
РВ
РВ
РВ
3
2
6
4
3
2
2
.
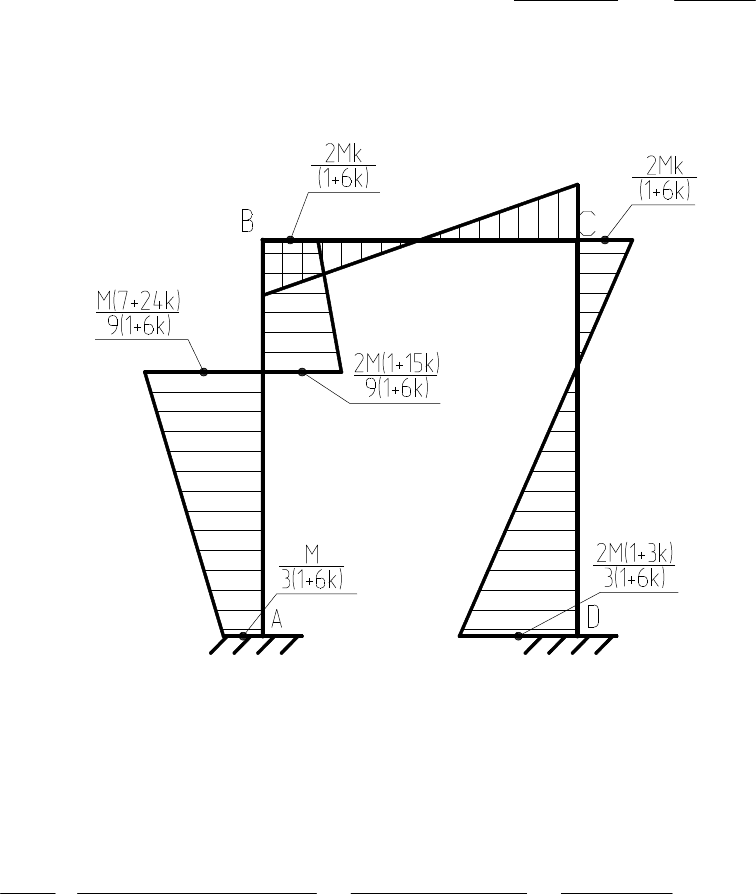
4. Ординаты эпюры изгибающих моментов в узловых точках же-
сткой рамы (рис. 45).
Рис. 45. Расчетная схема ординат эпюры
изгибающих моментов
Вертикальная стойка АВ.
По методу сил:
;
)К(
МК
)НL(
МН
)НL(L
МНL
М
РВРП
РВ
РВРПРП
РВРП
В
61
2
6
2
6
4
2
