Левшунов В.М Инженерные конструкции
Подождите немного. Документ загружается.


101
Эксцентриситет расчетной продольной силовой нагрузки
относительно центра тяжести арматуры в растянутой зоне бетона
определяется с учетом продольного изгиба: e
s
= e
p
К
λ
+ (0.5h – a
sc
).
Сжатая зона бетона устанавливается из условия статической
устойчивости поперечного сечения на расчетную продольную
силовую нагрузку при оптимальном армировании по симметричной
схеме:
bR/bh)R(Nх
bbоптsscp 2
][
,
где σ
s
– нормальное напряжение, воспринимаемое арматурой в растя-
нутой зоне бетона при ξ ≥ ξ
R
.
Нормальные напряжения в арматуре растянутой зоны бетона
устанавливаются расчетом в зависимости от предельного значения
относительной высоты сжатой зоны бетона при оптимальном
армировании:
],
)h/х(
[R
R
o
ss
1
1
12
где ξ
R
– предельное значение относительной высоты сжатой зоны
бетона.
Если выражение для σ
s
подставить в выражение для х, то получим
расчетную зависимость для сжатой зоны бетона прямоугольного
сечения малых эксцентриситетов следующего построения:
.
bR
bh]}
)h/х(
[RR{N
х
bb
опт
R
sscp
2
0
1
1
12
Расчет сжатой зоны бетона по этой расчетной зависимости вы-
полняется методом последовательных приближений x к расчетному
значению.
Последовательность расчетов на прочность прямоугольных сече-
ний малых эксцентриситетов незначительно отличается от последо-
вательности расчетов на прочность прямоугольных сечений больших
эксцентриситетов и состоит из следующих примерных разделов.
1. Устанавливается начальный эксцентриситет е
р
расчетной
продольной силовой нагрузки с учетом случайного эксцентриситета е
с
.
2. Устанавливается расчетный эксцентриситет расчетной про-
дольной силовой нагрузки с учетом продольного изгиба е
р
К
λ
и
определяется расчетный случай малых эксцентриситетов по е
р
К
λ
<
0.3h
o
≥ 0.15h
o
.
102
3. Выполняется расчет сжатой зоны бетона x и уточняется
расчетный случай малых эксцентриситетов по ξ = х/h
o
≥ ξ
R
.
4. Устанавливается коэффициент влияния относительной высоты
сжатой зоны бетона на величину изгибающего момента, воспри-
нимаемого сжатой зоной бетона К
b
.
5. Устанавливается эксцентриситет расчетной продольной сило-
вой нагрузки относительно центра тяжести арматуры в растянутой
зоне бетона е
s
.
6. Устанавливается требуемая площадь поперечного сечения
арматуры в сжатой и растянутой зоне бетона A
sc
= A
s
≥ (γ
b2
R
b
ξbh
o
–
N
p
)/σ
s
.
7. По сортаменту расчетных характеристик подбирается арматура
соответствующего класса и выполняется расчет процента симмет-
ричного армирования μ.
6.4. Примеры инженерных расчетов
Пример 1. Установить размеры прямоугольного сечения слу-
чайных эксцентриситетов колонны многопролетного сооружения из
монолитного железобетона класса В15 (γ
b2
R
b
= 7.7 МПа) и подобрать
арматуру класса А300 (R
sc
= 270 МПа). Расчетная продольная силовая
нагрузка N
p
= 900 кН. Полная высота колонны Н = 6.0 м.
Расчеты.
1. Требуемая площадь прямоугольного сечения при К
φ
= 1.0 и
A
sc
μ
опт
A
b
= 0.01A
b
должна быть не менее A
b
= bh ≥ N
p
/(γ
b2
R
b
+ μ
опт
R
sc
)
= (900∙10
3
)/[(7.7∙10
2
) + 0.0/1∙(270∙10
2
) = 857 см
2
.
Принимаем квадратное поперечное сечение колонны и получаем:
A
b
= bh = 30x30 = 900 см
2
.
2. Коэффициент продольного изгиба при показателе гибкости
λ = L/h = 1.2∙600/30 = 24 и коэффициенте прочностных характеристик
арматуры и бетона К
R
= μ
опт
(R
sc
/γ
b2
R
b
) = 0.01∙(270/7.7) = 0.36 К
φ
= К
λ
+
+2(К
μ
– К
λ
)К
R
= 0.62 + 2∙(0.63 – 0.62)∙0.36 = 0.63 (табл. 117 [16]).
3. Требуемая площадь поперечного сечения арматуры A
sc
≥ N
p
/
γ
φ
R
sc
– γ
b2
R
b
A
b
/R
sc
= (900∙10
3
)/[0.63∙(270∙10
2
)] –[(7.7∙10
2
)∙900]/(270∙10
2
)
= 26.2 см
2
.
4. Расчетный процент армирования μ = (А
sc
/A
b
)∙100% =
(26.2/900)∙100% = 2.91% > μ
опт
= 0.8…1.5% (табл. 116 [16]).
103
Так как расчетный процент армирования больше оптимального,
выполняем корректировку размеров поперечного сечения в большую
сторону.
Принимаем А
b
= bh = 35∙35 = 1215 см
2
и получаем при λ = 720/35
= 20 и К
R
= 0.36 К
φ
= 0.62 + 2∙(0.63 – 0.62)∙0.36 = 0.63 (табл. 117 [16]),
A
sc
= (900∙10
3
)/[0.63∙(270∙10
2
)] – [(7.7∙10
2
)∙1215]/(270∙10
2
) = 17.3 см
2
;
μ = (17.3/1215)∙100% = 1.41% (в пределах оптимальных значений,
табл. 116 [16]).
5. По сортаменту расчетных характеристик подбираем 6 стерж-
ней горячекатаной арматуры класса А300 диаметром 20 мм, общая
площадь поперечного сечения которых А
sc
= 18.9 см
2
.
6. Статическая устойчивость поперечного сечения на расчетную
продольную силовую нагрузку N
p
≤ К
φ
γ
b2
R
b
A
b
+ R
sc
A
sc
. N
p
= (900∙10
3
).
γ
b2
R
b
A
b
= < 0.63∙(7.7∙10
2
)∙1215 + (270∙10
2
)∙18.9. 900 кН < 1123 кН.
Пример 2. Подобрать арматуру класса А300 (R
s
= R
sc
=270 МПа,
Е
s
= 20∙10 МПа) для колонны 40х40 см
2
из монолитного железобе-
тона класса В30 (γ
b2
R
b
=15.3 МПа, Е
b
=32∙10
3
МПа) однопролетного
сооружения. Расчетная продольная силовая нагрузка N
p
= 900 кН.
Расчетная моментная нагрузка М
р
= 200 кНм. Полная высота колон-
ны Н
= 6.0 м.
Расчеты.
1. Случайный эксцентриситет расчетной продольной силовой
нагрузки е
с
= h/30 = 40/30 = 1.33 см < L/600 = 1.5∙600/600 = 1.5 см >
1.0 см. Принимаем е
с
= 1.5 см.
2. Начальный эксцентриситет расчетной продольной силовой
нагрузки е
р
= М
р
/N
p
+ е
с
= (200∙10
5
)/(900∙10
3
) + 1.5 = 23.7 см.
3. Показатель гибкости λ = L/h = 600/40 = 22.5 > 4.0. Требуется
расчет критической продольной силовой нагрузки.
4. Относительная величина начального эксцентриситета расчет-
ной продольной силовой нагрузки е
о
= е
р
/h = 23.7/40 = 0.59.
5. Приведенный момент инерции арматуры относительно центра
тяжести поперечного сечения колонны при оптимальном армирова-
нии μ
опт
= 0.01 и защитном слое бетона а
s
= a
sc
= 5 см J
s
= μ
опт
bh[(h
o
–
a
sc
)/2]
2
= 0.01∙40
2
∙{[(40 – 5) – 5]/2}
2
= 3600 см
4
.
6. Критическая продольная сила

104
59.01.0
11.0
(
24
40
[
)6005.1(
10)1032(4.6
])1.0
1.0
11.0
(
2
[
4.6
4
2
23
2
b
s
s
o
bb
E
E
J
e
J
L
E
N
3
4
10
32
1020
3600)1,0
10061 кН > N
p
= 900 кН.
7. Коэффициент продольного изгиба К
λ
= 1/(1 – N
p
/N
λ
) = 1/(1 –
900/10061) = 1.10.
8. Расчетный эксцентриситет расчетной продольной силовой
нагрузки относительно центра тяжести арматуры в растянутой зоне
бетона e
s
= e
p
К
λ
+ (0.5h – a
s
) = 23.7∙1.10 + (0.5∙40 – 5) = 41.1 см.
9. Высота сжатой зоны бетона по схеме симметричного
армирования поперечного сечения (А
s
=A
sc
) x = N
p
/γ
b2
R
b
= (900∙10
3
)/
/[(15.3∙10
2
)∙40] = 14.7 см.
Так как ξ = х/h
o
= 14.7/(40 – 5) = 0.420 < ξ
R
= 0.585 и е
р
К
λ
=
26.1 см > 0.3h
o
= 10.5 см, то расчеты на прочность выполняем для
расчетного случая больших эксцентриситетов.
10. Коэффициент влияния относительной высоты сжатой зоны
бетона на величину изгибающего момента, воспринимаемого сжатой
зоной бетона: К
b
= ξ(1–0.5ξ) = 0.420∙(1–0.5∙0.420) = 0.332 < К
bR
=
0.422.
11. Требуемая площадь поперечного сечения арматуры в сжатой
зоне бетона A
sс
≥ (N
p
e
s
– γ
b2
R
b
bh
o
2
)/[R
sc
(h
o
– a
sc
)] = [(900∙10
3
)∙41.1 –
(15.3∙10
2
)∙0.332∙40∙35
2
]/[(270∙10
2
)∙(35 – 5)] = 14.4 см
2
.
12. Требуемая площадь поперечного сечения арматуры в
растянутой зоне бетона A
s
≥ (γ
b2
R
b
ξbh
o
– N
p
)/R
s
+ A
sc
(R
sc
/R
s
) =
[(15.3∙10
2
)∙0.420∙40∙35–(900∙10
3
)]/(270∙10
2
)+ 14.4∙(270/270) =14.4 см
2
.
13. По сортаменту расчетных характеристик для армирования
поперечного сечения по симметричной схеме (А
s
= A
sc
= 14.4 см
2
)
подбираем 6 стержней горячекатаной арматуры класса А300 диамет-
ром 18 мм, общая площадь поперечного сечения которых 15.3 см
2
.
14. Расчетный процент армирования μ = [(A
s
+ A
sc
)/bh]∙100% =
= (30.6/1600)∙100% = 1.91% (не превышает допустимых пределов,
табл. 116 [16]).
Пример 3. Подобрать арматуру класса А300 (R
s
= R
sc
= 270 МПа)
для колонны прямоугольного сечения 40х40 см
2
из монолитного
железобетона класса В-30 (γ
b2
R
b
= 15.3 МПа) однопролетного
сооружения. Расчетная продольная нагрузка N
p
= 1300 кН. Расчетная
моментная нагрузка М
р
= 50 кНм. Полная высота колонны Н = 6.0 м.

105
Расчеты.
1. Начальный эксцентриситет расчетной продольной силовой
нагрузки с учетом случайного эксцентриситета е
р
= М
р
/N
p
+ e
c
=
(50∙10
5
)/(1300∙10
2
) + 1.5 = 5.3 см.
2. Коэффициент продольного изгиба при N
λ
= 10061 кН К
λ
1/(1 –
N
p
/N
λ
) = 1/(1 – 1300/10061) = 1.15.
3. Расчетный эксцентриситет расчетной продольной силовой
нагрузки e
s
= e
p
γ
λ
+ 0.5h – a
s
) = 7.1∙1.10 +(0.5∙40 – 5) = 22.4 см.
Так как е
р
К
λ
= 5.3∙1.15 = 6.1 см < 0.3h
o
= 10.5 см, имеем
расчетный случай малых эксцентриситетов.
4. Сжатая зона бетона для прямоугольного сечения малых
эксцентриситетов при оптимальном проценте симметричного
армирования
bR
bh]}
)h/х(
[RR{N
х
bb
опт
R
o
sscp
2
1
1
12
=
.
).(
.]}
.
)/х(
)[(){()(
4010315
400101
60501
3512
1027010270101300
2
2223
Задачу по расчету сжатой зоны бетона решаем методом
последовательных приближений.
Первое приближение 217
10612
10248101300
см25
2
33
.
см.
Второе приближение 321
10612
105101300
см121
2
33
..
см.
Третье приближение 321
10612
102101300
см221
2
33
..
. см.
Окончательно принимаем сжатую зону бетона x = 21.3 см и
уточняем расчетный случай малых эксцентриситетов: ξ = х/h
o
=
= 21.3/35 = 0.609 > ξ
R
= 0.585.
4. Коэффициент влияния относительной высоты сжатой зоны
бетона на величину изгибающего момента, воспринимаемого сжатой
зоной бетона: К
b
= 0.609∙(1 – 0.5∙0.609) = 0.424 > К
bR
= 0.414.
5. Эксцентриситет расчетной продольной нагрузки относительно
центра тяжести арматуры в растянутой зоне бетона e
s
= e
p
К
λ
+ (0.5h –
– a
s
) = 6.1 + (0.5∙40 – 5) = 21.1 см.

106
6. Требуемая площадь поперечного сечения арматуры в сжатой
зоне бетона A
sc
≥ (N
p
e
s
– γ
b2
R
b
bh
o
2
)/[R
sc
(h
o
– a
sc
) = [(1300∙10
3
)∙21.1 –
– (15.3∙10
2
)∙40∙35
2
]/[(270∙10
2
)∙(35 – 5)] = –84.9 см
2
.
Так как А
sc
< 0, то арматура в сжатой зоне бетона принимается
конструктивно и в расчетах требуемой площади поперечного сечения
арматуры в растянутой зоне бетона не учитывается.
7. Требуемая площадь поперечного сечения арматуры в растяну-
той зоне бетона
s
pobb
s
NbhR
A
2
]1
605
.
0
1
)35/3.211(2
[)10280(
)101300(3540609.0)103.15(
2
32
= 6.95 см
2
.
8. По сортаменту расчетных характеристик подбираем 4 стержня
горячекатаной арматуры класса А300 диаметром d
s
= 16 мм, общая
площадь попреречного сечения которых А
s
= 8.04 см
2
.
9. Расчетный процент симметричной схемы армирования μ = [(A
s
+A
sc
)/bh]∙100% = [(8.04 + 8.04)/40∙40]∙100% =1.0% (соответствует
оптимальному значению).
6.5. Контрольные вопросы
1. Какие существуют виды сжатых элементов строительных
конструкций из монолитного железобетона.
2. Приведите общую последовательность расчетов внецентренно
сжатых конструкций с прямоугольным сечением
РАЗДЕЛ 7. ЖЕСТКИЕ РАМЫ
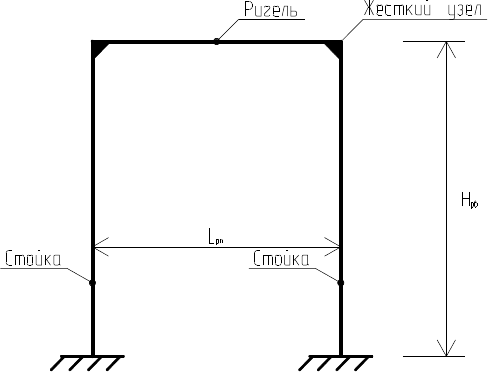
Жесткая рама П-образного вида с жестким закреплением опор-
ных частей вертикальных стоек из монолитного железобетона пред-
ставляет собой простейшую статически неопределимую строитель-
ную конструкцию. Вертикальные стойки и ригель образуют также
жесткие узлы в местах своего соединения (рис. 33).
107
Рис. 33. Расчетная схема жесткой рамы П-образного вида
Поперечное сечение жесткой рамы, как правило, прямоугольное.
Отдельные участки вертикальных стоек могут иметь различные раз-
меры поперечного сечения в зависимости от абсолютных значений
внецентренного нагружения. Ригель жесткой рамы воспринимает на-
грузку, вызывающую плоский поперечный изгиб. Все это свидетель-
ствует о сложности статических расчетов жестких рам.
7.1. Статические расчеты жестких рам
Статические расчеты жестких рам заключаются в том, чтобы рас-
крыть статическую неопределимость и установить ординаты эпюры
изгибающих моментов, поперечных и продольных сил в поперечных
сечениях вертикальных стоек и ригеля. Такой расчет выполняется ме-
тодом сил.
Метод сил представляет собой совокупную последовательность
статических расчетов, позволяющих заменить лишние жесткие связи
рамы единичными лишними неизвестными.
Примечание. Единичность лишних неизвестных состоит в том, что их ве-
личина принимается равной единице для конкретной основной системы жест-
кой рамы.
Основная система жесткой рамы выбирается с таким расчетом,
чтобы она отвечала следующим условиям статической устойчивости:
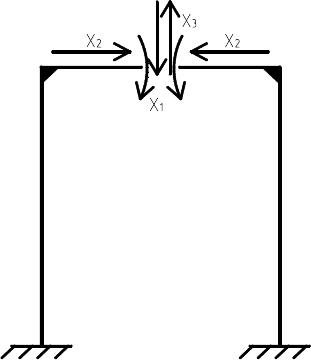
108
– геометрическая изменяемость не нарушена и жесткость узло-
вых соединений сохранена;
– статическая неопределенность раскрыта;
– количество лишних неизвестных минимальное.
Если ригель жесткой рамы разрезать на две части по вертикаль-
ной оси симметрии жесткой рамы П-образного вида, то можно полу-
чить основную систему, отвечающую условиям статической устойчи-
вости (рис. 34).
Рис. 34. Расчетная схема основной системы
жесткой рамы П-образного вида
Статическая устойчивость основной системы состоит в том,
что каждая из частей наделяется лишними неизвестными с таким
расчетом, чтобы канонические уравнения метода сил для раскрытия
статической неопределимости жесткой рамы были простые.
7.2. Канонические уравнения метода сил
Канонические уравнения метода сил представляют собой уравне-
ния перемещений точек приложения лишних неизвестных по линии
действия лишних неизвестных и по линии действия расчетной на-
грузки:
,0
;0
;0
3333232131
2323222121
1313212111
F
F
F
XXX
XXX
XXX
109
где δ
i
– перемещение точки приложения лишних неизвестных по ли-
нии действия лишних неизвестных;
Δ
i
– перемещение точки приложения лишних неизвестных по ли-
нии действия расчетной нагрузки;
Х
i
– лишние неизвестные.
7.3. Методика статических расчетов
Методика статических расчетов основывается на том, что верти-
кальные стойки и ригель жесткой рамы рассматриваются как двух-
опорные статически определимые балки с шарнирами на опорах, про-
леты которых загружаются расчетной нагрузкой, а шарнирные опоры –
расчетными изгибающими моментами в узловых соединениях.
Ординаты эпюры изгибающих моментов устанавливаются в уз-
ловых точках рамы как алгебраическая сумма ординат изгибающих
моментов лишних неизвестных и расчетной нагрузки:
М = М
1
Х
1
+ М
2
Х
2
+ М
3
Х
3
+М
F
,
где М
i
– ординаты эпюры изгибающих моментов лишних неизвест-
ных;
М
F
– ординаты эпюры изгибающих моментов расчетной нагрузки.
Ординаты эпюры поперечных сил устанавливаются расчетом:
Q = Q
o
+ (M
пр
+ М
лв
)/L,
где Q
o
– ординаты эпюры поперечных сил расчетной нагрузки в про-
лете;
М
пр
– ординаты эпюры узлового изгибающего момента на правой
шарнирной опоре;
М
лв
– то же на левой опоре;
L – расчетная длина пролета балки с шарнирами на опорах.
Ординаты эпюры продольных сил устанавливаются по ординатам
эпюры поперечных сил в узловых соединениях рамы.
Примечания: 1. Ординаты эпюры изгибающих моментов считаются поло-
жительным, если растягиваются нижние волокна.
2. Ординаты эпюры поперечных сил считаются положительными, если
создают вращение по часовой стрелке.
3. Ординаты эпюры продольных сил считаются положительными, если вы-
зывают внецентренное растяжение.
110
Ординаты эпюры изгибающих моментов, поперечных и продоль-
ных сил могут быть установлены по расчетным формулам Д.В. Быч-
кова.
Расчетные формулы Д.В. Бычкова представляют собой расчет-
ные зависимости ординат эпюры изгибающих моментов, поперечных
и продольных сил в узловых соединениях рамы и в любом попереч-
ном сечении вертикальных стоек и ригеля, полученные на основе ка-
нонических уравнений метода сил.
7.4. Примеры статических расчетов
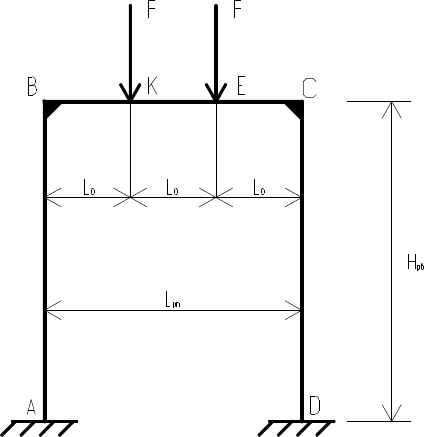
Пример 1. Выполнить статический расчет жесткой рамы П-
образного вида, нагруженной симметричной силовой сосредоточен-
ной нагрузкой на ригель постоянного сечения (рис. 35).
Рис. 35. Расчетная схема нагружения жесткой рамы
симметричной силовой сосредоточенной нагрузкой
Расчеты по методу сил.
1. Единичные эпюры изгибающих моментов лишних неизвестных
для основной системы метода сил (рис. 36).
2. Единичные перемещения точек приложения лишних неизвест-
ных по линии действия лишних неизвестных:
