Леушин А.М., Нигматуллин Р.Р., Прошин Ю.Н. Теоретическая механика (практический курс). Задачник для физиков

Подождите немного. Документ загружается.

Теоретическая физика. Механика (практический курс) 41

Метод законов сохранения и движение в центральном

поле

Раздел 3. Метод законов сохранения и движение

в центральном поле

Минимальные теоретические сведения

Законы изменения и сохранения физических величин и интегралы

движения

Как было продемонстрировано в предыдущем разделе, задача о дви-

жении одной частицы имеет общее решение для сравнительно широкого

класса сил. Проблему движения двух частиц также можно решить в квад-

ратурах при достаточно общих допущениях о силе взаимодействия между

частицами (см. следующий раздел). Однако задача трех и большего коли-

чества частиц при общих предположениях о силах взаимодействия встре-

чает непр

еодолимые трудности. Известны только некоторые частные ре-

шения этой задачи или решения для очень узкого класса взаимодействий.

В связи с этим приобретают огромное значение общие теоремы, спра-

ведливые при любом числе частиц, которые часто позволяют получить

общие результаты без решения систем дифференциальных уравнений или

контроли

ровать правильность приближенных решений. Такими универ-

сальными теоремами являются законы изменения и сохранения импульса,

момента и энергии механической системы.

Законы сохранения физических величин приводят к интегралам дви-

жения.

Интегралом движения называется такая функция времени, коорди-

нат и скоростей частиц, которая при движении механической системы со-

храняет постоянное значение, определяемое начальными условиями. Инте-

гралы движения, содержащие скорости частиц, называются

первыми инте-

гралами движения. Вторыми интегралами движения называются такие

функции времени, координат частиц и произвольных констант, которые

при движении системы сохраняют постоянные значения.

Наличие интегралов движения существенно облегчает решение сис-

Метод законов сохранения и движение в центральном поле 42

темы уравнений движения. Знание, например, s независимых первых инте-

гралов движения дает возможность понизить порядок системы дифферен-

циальных уравнений на

s. Для механической системы, состоящей из N час-

тиц, система 6

N первых интегралов или 3N вторых интегралов движения

эквивалентны общему решению уравнений движения.

Сами законы сохранения, следовательно, и интегралы движения, яв-

ляются следствием законов изменения физических величин со временем −

их частными случаями.

Закон изменения импульса системы N материаль-

ных точек

P получается на основе второго закона Ньютона и имеет вид

, (3.1)

где

ex ex

∑

− сумма всех внешних сил, действующих на точки систе-

мы. Для

замкнутой, или изолированной, системы, т.е. системы, взаимодей-

ствием которой с прочими, не входящими в нее телами, можно пренебречь,

внешние силы равны нулю и поэтому

const

===

∑

PP,

т.е. имеет место

закон сохранения импульса и импульс является первым

интегралом движения. Если система будет не замкнута, то в том случае,

когда проекция суммы всех внешних сил на некоторую

неподвижную ось

(скажем ось

z) в любой момент времени равна нулю, проекция импульса

системы на ту же ось будет сохраняться, т. е.

ziiz

PmzP

∑

Наряду с полным импульсом системы, важную роль в механике игра-

ет момент количества движения, или

момент импульса системы. Он опре-

деляется как сумма моментов импульса отдельных точек системы

[]

iii

ii==

∑∑

MM rp,

Теоретическая физика. Механика (практический курс) 43

где

r и

p − радиус-вектор и импульс i-ой точки системы. Закон изменения

момента импульса системы имеет вид

, (3.2)

где

ex ex

[]

∑

LrF − момент всех внешних сил, действующих на систему.

Для изолированной системы точек

L и из (3.2) получаем закон сохра-

нения момента количества движения

[]const

===

∑

Mrp M,

т.е. полный момент количества движения изолированной системы точек

остается постоянным и также является первым интегралом движения.

Введем полную потенциальную энергию системы

U = U

+ U

как

сумму ее потенциальной энергии во внешних полях

и внутренней по-

тенциальной энергии

()

ki ki

UUr=

∑

, где ()

ki ki

Ur − зависящая от рас-

стояния

между i-ой и k-ой точками потенциальная энергия их взаимо-

действия. Определяя

полную механическую энергию системы E = T + U как

сумму кинетической

T и полной потенциальной энергии U, можно полу-

чить

закон ее изменения со временем в виде

dE U

dt t

∂

== +

∂

. (3.3)

Из (3.3) следует, что изменение полной энергии обусловлено нестационар-

ностью внешнего потенциального поля и мощностью

()

∑

всех

диссипативных сил

d ex.d in.d

ii i

=+FF F, как внешних

ex.d

F , так и внутренних

in.d

F . Если диссипативные силы (внешние и внутренние) отсутствуют и ес-

ли потенциальная энергия системы во внешних полях не зависит явно от

времени, то полная механическая энергия системы

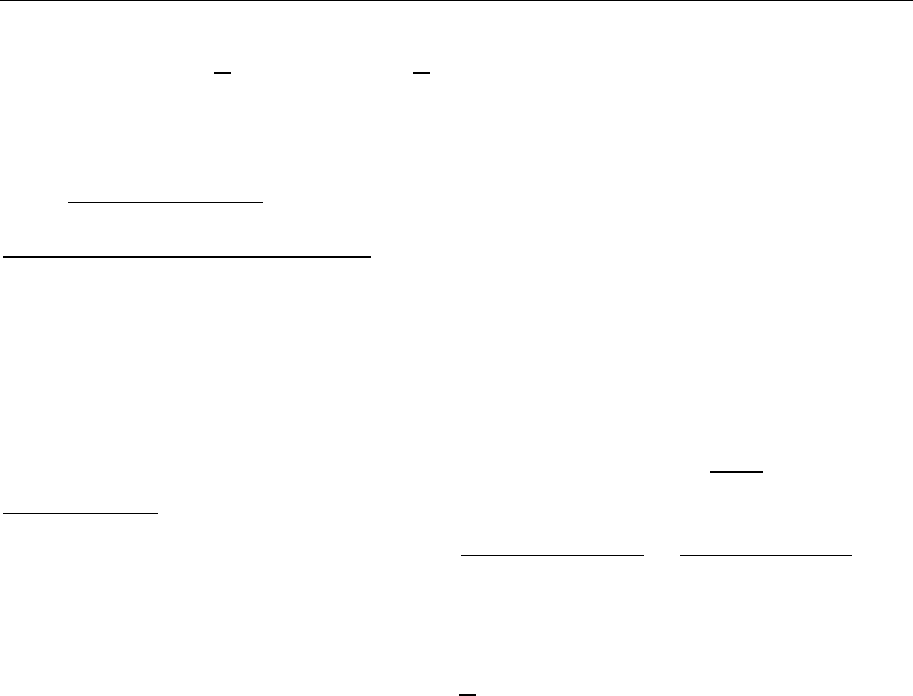
Метод законов сохранения и движение в центральном поле 44

2ex

()const

i i ki ki

iik

mv U U r E

=++ ==

∑∑

будет сохраняться, т.е. будет интегралом движения. Такую систему назы-

вают

консервативной.

Движение в центральном поле

Использование законов сохранения и интегралов движения удобно

продемонстрировать на примере рассмотрения задачи о движении частицы

в центральном поле.

Если сила, действующая на частицу, направлена вдоль ее радиус-век-

тора (параллельно или антипараллельно ему), то такая

сила называется

центральной. Если к тому же модуль этой силы зависит только от величи-

ны радиус-вектора, то сила является

потенциальной и стационарной. То-

гда помещая начало системы координат в силовой центр, в соответствии с

(3.2) и (3.3) получим четыре первых скалярных интеграла движения

[] , ()

mEmvUrE

==+=MrvM

Из этих четырех интегралов независимы только три, поскольку три компо-

ненты момента импульса

, M

связаны между собой соотношением

() ([])0

=Mv r v v .

Наряду с первыми интегралами движения, в данной задаче можно

найти три вторых независимых интеграла. Один из них получается в ре-

зультате скалярного умножения вектора момента импульса

M на радиус-

вектор

() ([])0

xyz

Mx My Mz m=++= =Mr rv r

и представляет собой уравнение плоскости, в которой происходит движе-

ние частицы и которая оказывается перпендикулярной направлению со-

храняющегося момента

M . Два других вторых интеграла движения можно

получить направляя ось

z по вектору M и вводя на плоскости xOy поляр-

ные координаты

и ϕ . Для величины момента M и полной энергии час-

тицы

E тогда найдем

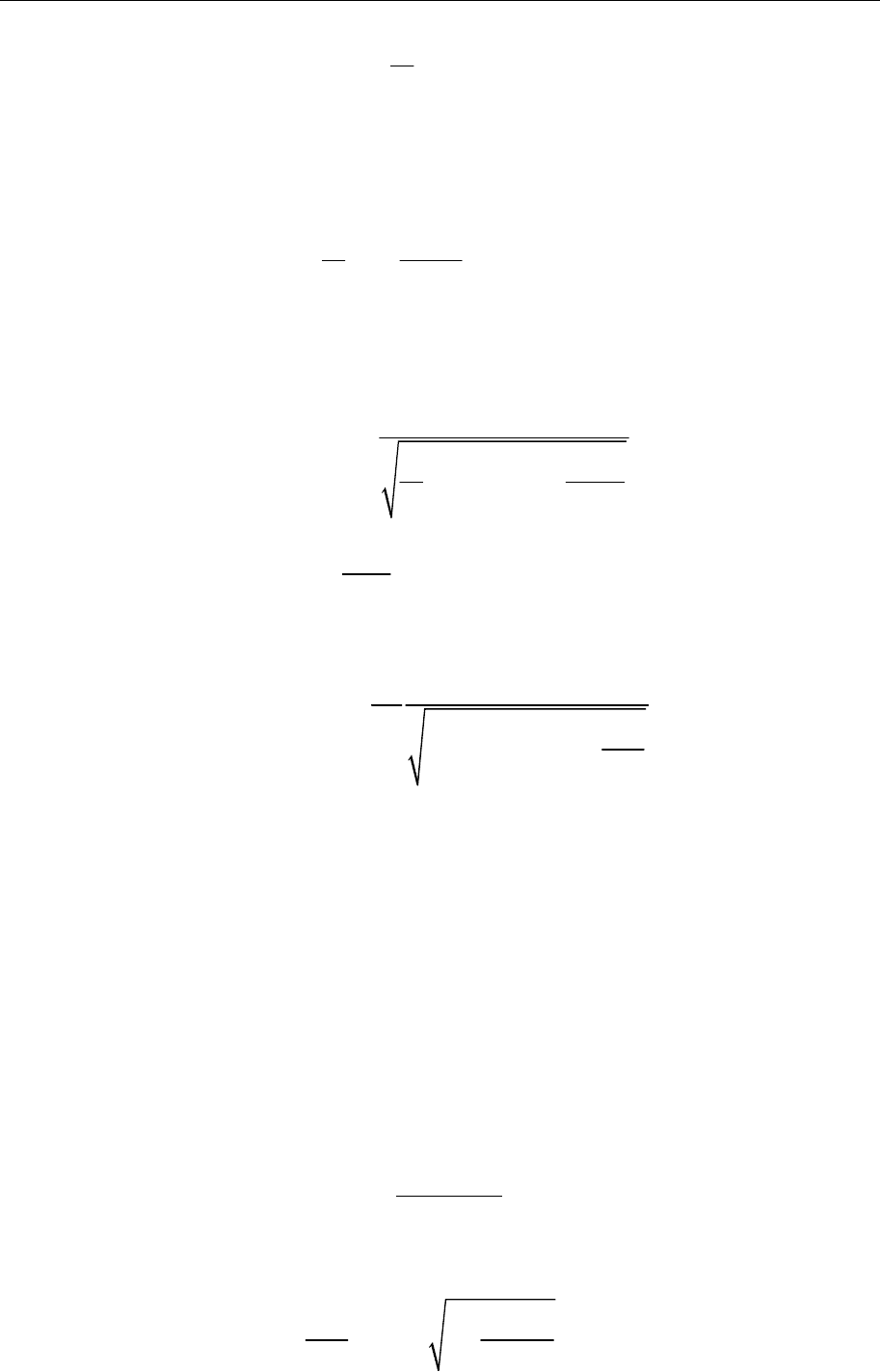
Теоретическая физика. Механика (практический курс) 45

2222

,()()

Mm E U

=ρϕ = ρ+ρϕ+ ρ

&&&

Выражая из 1-го соотношения

через

и подставляя во второе, для

энергии частицы будем иметь

()

=ρ+ +ρ

Разделяя в этом уравнении переменные и интегрируя по времени от 0 до t,

получаем еще один второй интеграл в виде

[]

const

()

==−

−ρ−

∫

. (3.4)

Далее, написав dϕ как

ddt

ϕ=

и интегрируя по

от 0 до ϕ , находим

3-ий второй интеграл движения

[]

const

2()

mE U

==ϕ−

−ρ−

∫

. (3.5)

Формулы (3.4) и (3.5) в общем виде решают поставленную задачу. Вторая из

них определяет связь между координатами

, т.е. дает уравнение траек-

тории на плоскости, в то время как первая определяет в неявном виде рас-

стояние

ρ двигающейся частицы от силового центра как функцию времени.

В частности, для силы притяжения, меняющейся обратно пропорцио-

нально квадрату расстояния до силового центра, т.е. для потенциальной

энергии () /U ρ=−αρ с α > 0 (проблема Кеплера), из (3.5) получим урав-

нение траектории в виде

()

1cos

ρϕ =

εϕ

(3.6а)

с параметрами p и ε , определяемыми соотношениями

=ε=+

. (3.6б)

Метод законов сохранения и движение в центральном поле 46

Примеры решения задач

Задача 1. Автомобиль заданной массы m движется таким образом, что раз-

виваемая им мощность в процессе движения сохраняет свое постоянное

значение. Показать, что путь, проходимый автомобилем, изменяется со

временем по закону S(t) = at

3/2

. Считать, что в начальный момент времени

его скорость равна нулю.

Решение. Для связи мощности со скоростью движения воспользуемся за-

коном изменения кинетической энергии, который следует из (3.3),

. (3.7)

Здесь N

− мощность всех сил (включая и внутренние), действующих на ав-

томобиль. По условию задачи N

является величиной постоянной. Интег-

рируя уравнение (3.7) с учетом начальных условий получим, что величина

скорости меняется по закону

v(t) =

1/2

1/ 2

⎛⎞

⎜⎟

⎝⎠

. (3.8)

Определив закон изменения скорости и интегрируя (3.8) с учетом соотно-

шения ds/dt = v(t), находим искомый закон изменения s(t)

s(t) =

1/ 2

3/2

⎛⎞

⎜⎟

⎝⎠

. (3.9)

Последняя формула (3.9) дает решение поставленной задачи.

Замечание. Получите решение для s(t), если в начальный момент времени

скорость автомобиля v

≠ 0.

()

3/2

() 2 /

st v N mt

⎡⎤

⎢⎥

⎣⎦

Задача 2. Найти закон движения частицы массы m и заряда e в магнитном

поле

H(0,0,H

cos(y/a)). Начальные условия в декартовых координатах

имеют вид

r(0) = 0, v(0) = (0, ωa, 0), где ω = eH

/mc.

Решение задачи. Умножив векторное уравнение движения

Теоретическая физика. Механика (практический курс) 47

[]

dt c

(3.10)

скалярным образом сначала на скорость

v, а затем на орт e

|| H, можно по-

лучить следующие интегралы движения:

()

0const

⎛⎞

=→ = =

⎜⎟

⎝⎠

()

0const

zzz

⎛⎞

=→ = =

⎜⎟

⎝⎠

eve

Учет начальных условий приводит к следующему выражению

222

yv+=

= ω

, (3.11а)

Разделив на массу x-компоненту уравнения (3.10), имеем

[]

cos( / ) 0 sin( / ) 0 sin( / ) const

dx d

yya xaya xaya

dt dt

−ω = → −ω = → −ω =

&& &

Опять используя начальные условия, получаем

sin( / )

aya

. (3.11б)

Из системы двух уравнений (3.11) находим

2222

cos ( / )ya ya=ω

. (3.12)

Интегрируя (3.12), получаем

ωt =

1sin(/)

cos( / ) 1 sin( / )

dy y a

aya ya

−

∫

. (3.13)

Из уравнений (3.11а), (3.13) находим закон движения частицы

= (aω)th(ωt), x(t) = aln[ch(ωt)], (3.14а)

y(t) = aarcsin[th(ωt)]. (3.14б)

Задача 3. Найти закон движения заряда в радиально-симметричном (т.е.

не зависящем от азимутального угла ϕ) магнитном поле

H = H

Φ(ρ)e

. На-

чальные условия в полярных координатах имеют вид

r(0) = (ρ

, ϕ

v(0) = (v

(0), ρ

, 0); ω

= eH

/mc.

Решение. Магнитная компонента силы Лоренца в полярных координатах

принимает вид

= () ()

eH d eH d

cdt cdt

ϕρ

ρΦ ρ − Φ ρ

ee.

Уравнения Ньютона в полярных координатах запишутся в виде

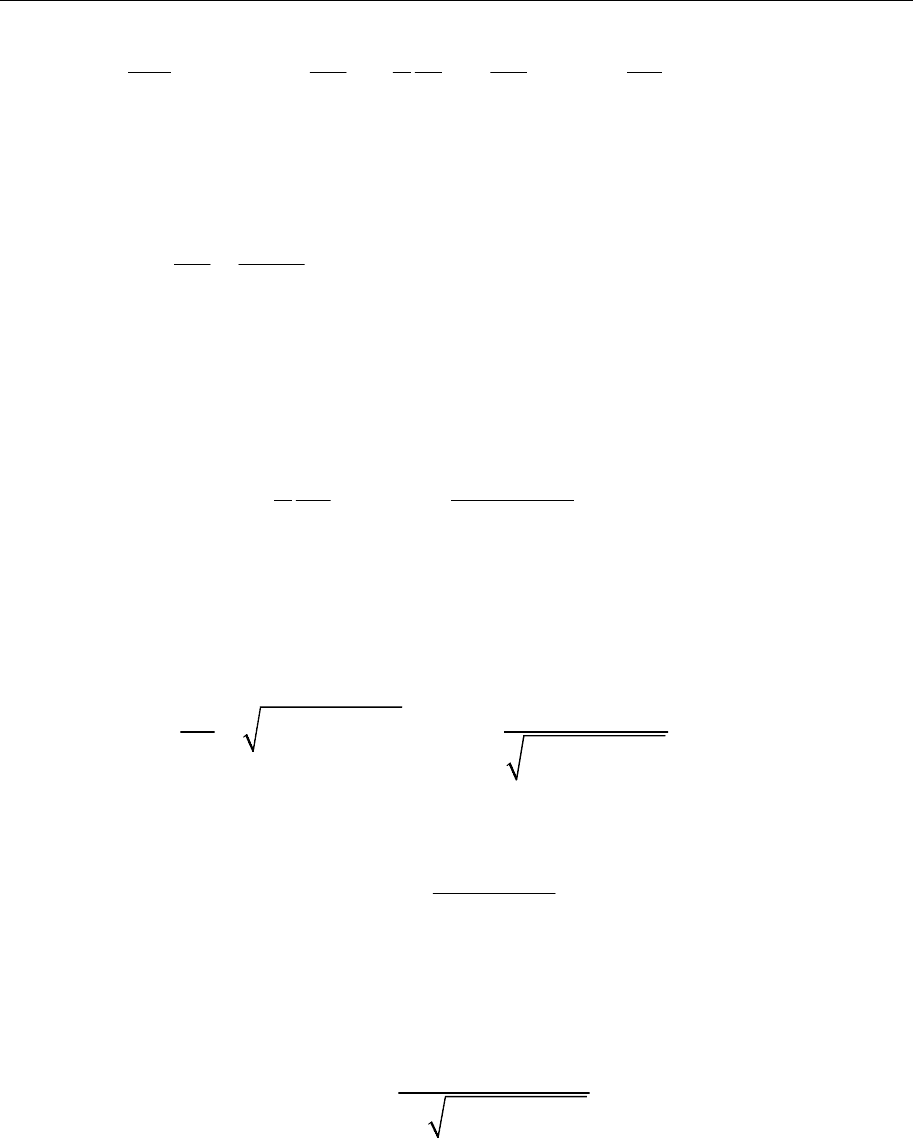
Метод законов сохранения и движение в центральном поле 48

() , ()

ddd d

dt dt dt dt dt

ϕϕρ

⎛⎞

=ω ρΦ ρ ρ =−ω Φρ

⎜⎟

⎝⎠

. (3.15)

Из последнего уравнения (3.15), переходя к новой независимой перемен-

ной ρ, получаем

()

,() ()

uudu

ϕρ

=ρ=ρω−ωΦ

∫

. (3.16)

Воспользовавшись определением радиальной компоненты скорости и учи-

тывая связь (3.16) угловой скорости и расстояния ρ, первое уравнение в

выражении (3.15) можно преобразовать к виду

()

1()()

ρρ

=ω

ρρ

. (3.17)

Интегрируя последнее уравнение с учетом начальных условий, получаем

квадратурные формулы для связи радиальной компоненты скорости и

пройденного радиального расстояния со временем

(0) ( ),

(0) ( )

ddu

vU t

vUu

=−ρ=

−

∫

. (3.18)

Здесь потенциальная функция определяется выражением

() ()

() 2

uMu

Udu

ρ=−ω

∫

. (3.19)

С учетом последних формул (3.18), (3.19) и связи (3.16) можно полу-

чить квадратурную формулу для искомой траектории

()

(0)

(0) ( )

Mudu

uv Uu

ϕ−ϕ =

−

∫

. (3.20)

Формулы (3.18) и (3.20) решают поставленную задачу. Решение этой

задачи повышенной трудности мы привели только по одной причине: пока-

зать, что существуют силовые поля, которые можно считать обобщением

стандартной задачи о движении материальной точки в центральном поле.

Любые точные решения нетривиальных уравнений Ньютона в квадратурах

Теоретическая физика. Механика (практический курс) 49

для произвольных сил представляют особую ценность для теоретической

механики.

Замечание. Рекомендуется воспроизвести и проверить эти общие форму-

лы, взяв для рассмотрения частный случай: Φ(ρ) = ρ.

Задачи

Обязательные задачи

3.1.

Материальная точка с массой m описывает окружность радиуса a,

притягиваясь некоторой точкой О этой окружности. Найти силу

притяжения и скорость точки как функции расстояния ρ до центра

притяжения (момент импульса материальной точки считать задан-

ным и равным М).

aMa

⎡⎤

=− =

⎢⎥

⎣⎦

3.2. Доказать, что при движении частицы в поле V(ρ) = −α/ρ, где α – по-

ложительная константа, величина

A = [v M] − αe

есть интеграл

движения. Найти траекторию частицы, используя при этом постоян-

ство вектора

А.

3.3.

Спутник движется вокруг Земли по эллиптической орбите с эксцен-

триситетом е. Найти отношение максимального ϕ

•

max

и минимально-

го ϕ

•

min

значений угловой скорости радиус-вектора спутника.

[ϕ

•

max

/ϕ

•

min

= (1 + e)

/(1 − e)

]

3.4. Первая космическая скорость v

определяется как минимальная ско-

рость, которую необходимо придать телу, чтобы оно стало искусст-

венным спутником планеты. Вторая космическая скорость v

опре-

деляется как минимальная скорость, которую должно иметь тело,

чтобы выйти из сферы влияния планеты, и начать инфинитное дви-

жение. Оценить величины этих скоростей для Земли и Луны.

1211З 1Л

,2,8/,1.7/vgRvv vкм сек v км сек

⎡⎤

== ≅ ≅

⎣⎦

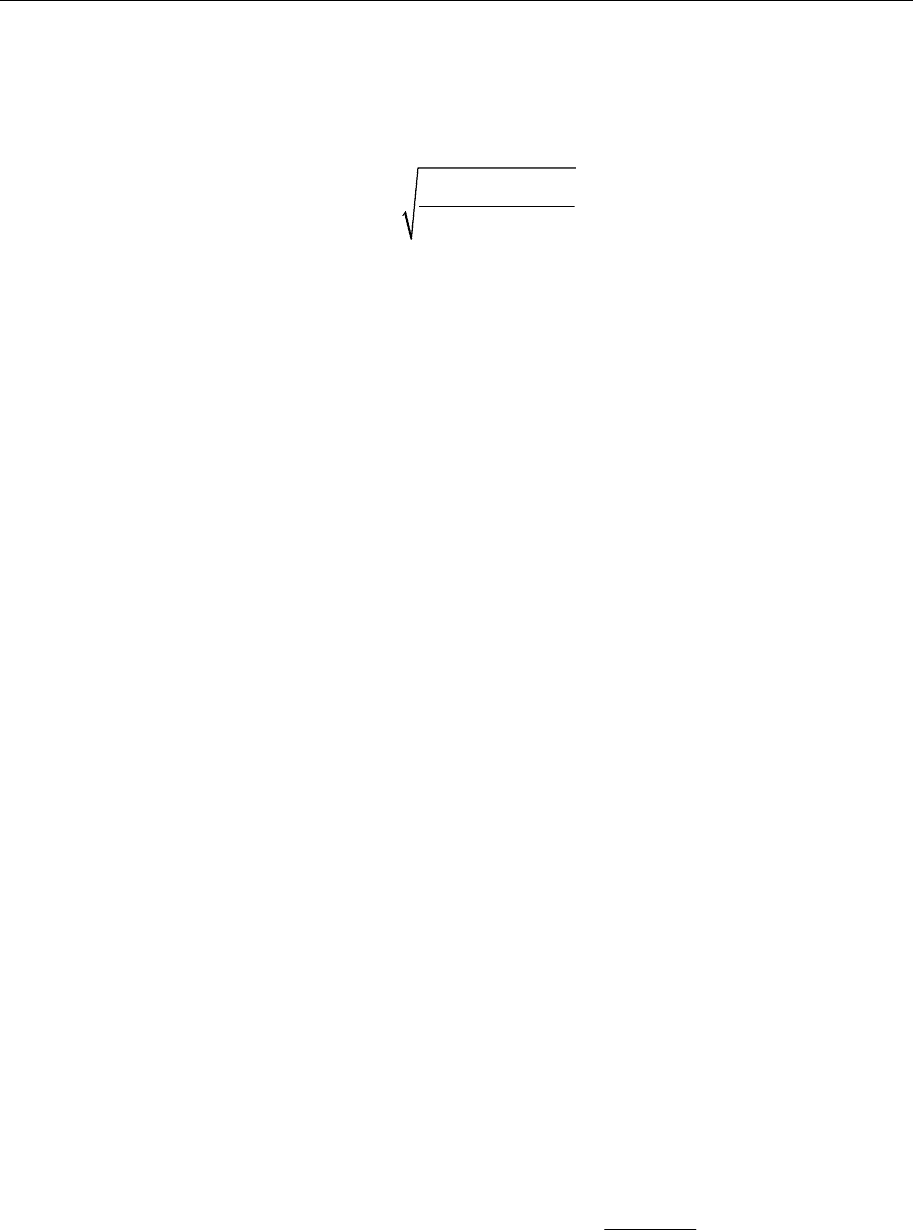
Метод законов сохранения и движение в центральном поле 50

3.5. Тело без начальной скорости падает на Землю с большой высоты Н.

Найти зависимость скорости тела от его текущей высоты h. Исследо-

вать случаи H/R << 1, h/R << 1 и H/R >> 1, h/R >> 1 (R − радиус Земли).

2( )

()

()( )

gR H h

RhRH

⎡⎤

−

⎢⎥

⎣⎦

3.6. Тело падает на Землю с большой высоты h. Пренебрегая сопротив-

лением воздуха, найти время Т, по истечении которого тело достиг-

нет поверхности Земли, и скорость, которую оно приобретет за это

время. Радиус Земли R предполагается известным.

3.7.

Найти траектории (изобразить их примерный вид) и закон движения

частицы в поле U = −U

(при r < R) и U = 0 (при r > R) (сферическая

потенциальная яма) при различных значениях начального момента

импульса М и энергии Е.

3.8.

Найти траектории движения частицы и изобразить их примерный

вид, если она двигается в потенциальном поле U(ρ).

а) U(ρ) = α/ρ + β/ρ

, (α > 0, β > 0);

б) U(ρ) = −α/ρ + β/ρ

, (α > 0, β > 0);

в) U(ρ) = −α/ρ − β/ρ

, (α > 0, 0< β < M

/2m);

г) U(ρ) = −α/ρ − β/ρ

, (α > 0, β > M

/2m).

3.9.

Показать, что в поле U = −α/r − (F

r), где F

– постоянная величина,

скалярная величина I = (

[vM]) − α(F

r)/r + [F

/2 является инте-

гралом движения.

3.10.

Обобщить теорему о вириале сил для заряженной частицы, движу-

щейся в однородном магнитном поле.

3.11.

Найти траекторию материальной точки, полная энергия которой при

движении в потенциальном поле

ln( / )

()

=−α равна нулю.

3.12.

Найти зависимость от координат потенциала центрального поля, в

котором материальная точка может двигаться по гиперболической

спирали /( )rpa b=ϕ+, где p, a, b – константы.