Леушин А.М., Нигматуллин Р.Р., Прошин Ю.Н. Теоретическая механика (практический курс). Задачник для физиков
Подождите немного. Документ загружается.


Теоретическая физика. Механика (практический курс) 191
113
1
2
212
2
31
3
L
p
qq
q
L
p
qq
q
L
pq
q
⎧
∂
==+
⎪
∂
⎪
⎪
∂
==
⎨
∂
⎪
⎪
∂
==
⎪
∂
⎩
&&
&
&
&
&
&
→
13
2
2
2
1
313
qp
p
q
q
qpp
⎧
=
⎪
⎪
=
⎨
⎪
⎪
=
−
⎩
&
&
&
.
Подставляем их в определение функции Гамильтона (9.3)
() ()
()
()
()
()
2
2
22
13 2 3 1 3 3 3 1 3
22
11
2
22 22
23
12 312 31 12 312
2
1
1
(,,)
2
11
222
2
pp
H t ppp ppp p ppp
qq
pp
qq qqq pp qq qqq
q
⎛⎞
=+ + −− +− −+
⎜⎟
⎝⎠
⎛⎞
++−+=+ −++−+
⎜⎟
⎝⎠
qp
.
Канонические уравнения Гамильтона тогда запишутся как
2
2
113223312
3
1
2
13 2 313
2
1
;;
;;
p
p
qq p q q p qq
q
p
qp q qpp
q
=−+ =−+ =+
===−
&&&
&&&
.
Задача 3. Найти функцию Лагранжа, если функция Гамильтона системы
имеет следующий вид
()
()
22
22
23
13 1 2 3 1 2
2
1
1
22
2
pp
H
pp q q q q q
q
=+++ +− +
.
Решение. По смыслу задача является обратной по отношению к предыду-
щей, а функция Гамильтона очень похожа на ответ предыдущей задачи.
Отличие в одном знаке. Нам нужно исключить "лишние" импульсы, после
чего воспользоваться соотношением (9.5).
С помощью уравнений Гамильтона, а именно,
q
•
j
= ∂H/∂p
j
составим
уравнения на неизвестные
p
j
и найдем их

Уравнения Гамильтона. Скобки Пуассона 192
13
1
2
2
2
2
1
313
3
H
qp
p
Hp
q
p
q
H
qpp
p
⎧
∂
==
⎪
∂
⎪
⎪
∂
⎪
==
⎨
∂
⎪
⎪
∂
==+
⎪
∂
⎪
⎩
&
&
&
→
113
2
212
31
p
qq
pqq
pq
=
−+
⎧
⎪
=
⎨
⎪
=
⎩
&&
&
&
.
Функция Лагранжа (9.5)
()()
22
1311213
1
(,,) (,,) ,(,,),
n
jj
j
L
tptqH ttqqqqqqq
=
=− =−+++−
∑
qq qq qpqq
&& &
&&&&&&&
()
()
()
()
()
22 2
22
12 1
131 1 2 312
222
22
112
13 1 2 3 1 2
1
222
1
22 2
qq q
qqq q q qqq
qqq
qq q q q q q
−− + − − − + + + =
=− + + − + + +
&&
&&&
&&
&&
,
Разница с функцией Лагранжа в задаче 2 также в одном знаке.
Задачи
Обязательные задачи
9.1. Составить функцию Гамильтона:
а) свободной материальной точки в цилиндрических и сферических
координатах;
б) частицы, двигающейся в однородном поле тяжести;
в) частицы в системе отсчета, вращающейся с постоянной угловой
скоростью
Ω.
9.2.
Найти функцию Гамильтона для частицы с зарядом e и массой m,
двигающейся в неоднородном электромагнитном поле со скаляр-
ным потенциалом
ϕ и векторным потенциалом А.
⎣
⎢
⎡
⎦
⎥
⎤
H =
1
2m
⎝
⎜
⎛
⎠
⎟
⎞
p +
e
c
A
2
+ e
ϕ
9.3. а) Найти функцию Гамильтона математического маятника, функция
Лагранжа которого (
ω – константа) L = ϕ
•
2
/2 − ω
2
(1 − cosϕ).

Теоретическая физика. Механика (практический курс) 193
б) Найти функцию Гамильтона этого математического маятника,
выбирая в качестве обобщенной координаты
x = [(1 − cosϕ)/2]
1/2
.
[]
б) H = p
2
(1 − x
2
/4)/2 + ω
2
x
2
/2
9.4. Найти функцию Гамильтона и составить канонические уравнения
движения механической системы, лагранжиан которой имеет вид
(
a, b – константы)
а) L = (q
•
2
1
+ q
•
2
2
)/2 − a(q
1
−q
2
)
2
/4 − b(q
1
+ q
2
)
2
/4;
б) L = (q
•
2
1
+ q
•
2
2
)/4a + (q
2
q
•
1
− q
1
q
•
2
)/2a + (q
2
1
+ q
2
2
)/4a;
в) L = q
•
2
1
/2 + (q
•
2
2
/2)sin
2
q
1
+ acosq
1
;
г
) L = (q
2
1
+ q
2
2
)(q
•
2
1
+ q
•
2
2
− 2a)/2;
д) L = q
•
1
q
•
2
− q
1
q
2
.
9.5.
Найти функцию Лагранжа механической системы, гамильтониан
которой имеет вид (
a, b, c – константы)
а) H =
p
2
2m
+ (ap) + U(r), a – постоянный вектор;
б) H = p
2
1
/6 + p
2
2
/2 + q
2
1
+
q
2
2
/2 + q
1
q
2
;
в) H = [p
2
1
+ 5p
2
2
− 2p
1
p
2
cos(q
1
− q
2
)]/{2[4 + sin
2
(q
1
− q
2
)]} −
− 3cosq
1
− cosq
2
;
г) H = (p
1
+ p
2
)
2
/(2at
2
) + p
2
2
/2 + acosq
2
;
д) H = p
2
1
/(4a) + p
2
2
/[4(c
2
+ b
2
cos
2
q
1
)];
е
) H = 2(q
1
p
2
1
+ q
2
p
2
2
)/(q
1
+ q
2
) + p
2
3
/(2q
1
q
2
) − a/(q
1
+ q
2
) + b(q
1
− q
2
);
ж
) H = p
2
1
+ p
2
2
+ 3p
2
3
+ 3p
2
4
− 2p
1
p
3
−2p
2
p
4
)/2+2(q
2
1
+
q
2
2
− q
1
q
2
) +
+ (q
2
3
+
q
2
4
)/4;
9.6.
Найти закон движения частицы, функция Гамильтона которой
H(x,p) = p
2
/2 + ω
2
0
x
2
/2 + λ(p
2
/2 + ω
2
0
x
2
/2)
2
.
[]
x = acos(ωt + ϕ), p = −aω
0
sin(ωt + ϕ), где ω = ω
0
(1 + 2λA), A = a
2
ω
2
0
/2
Уравнения Гамильтона. Скобки Пуассона 194
9.7. Найти функцию Гамильтона и составить канонические уравнения
движения для механических систем, описанных в задачах:
а) Задача 4, решенная в разделе 5 (уравнения Лагранжа);
б) 5.9; в) 5.11; г) 5.12;
д) 5.14; е) 5.15; ж) 5.16;
з) 5.19; и) 5.23.
9.8.
С помощью уравнений Гамильтона найти закон движения для час-
тицы с массой
m и зарядом е, двигающейся
а) в постоянном электрическом поле с потенциалом ϕ;
б) в постоянном магнитном поле H = He
z
с векторным потенциалом
A(0,Hx,0);
в) одновременно в постоянном электрическом и магнитном полях.
9.9.
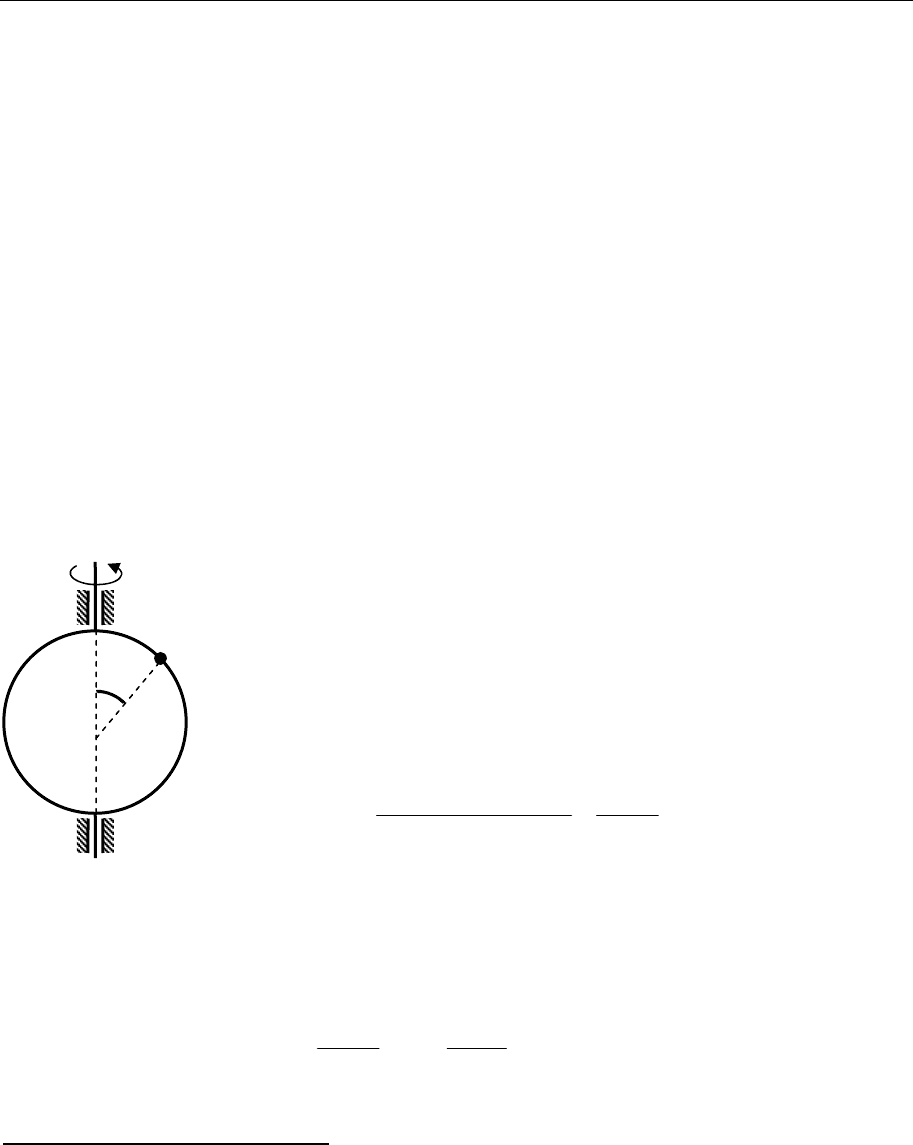
Тяжелое колечко массы m может скользить по
гладкой проволочной окружности массы
М и ра-
диуса
R, которая вращается вокруг своего верти-
кального диаметра. Написать функцию Гамиль-
тона и составить канонические уравнения системы.
22
222
cos
(2sin)2
pp
HmgR
RM m mR
ϕψ
⎡⎤
=
++ ψ
⎢⎥
+ψ
⎢⎥
⎣⎦
9.10. Составить канонические уравнения движения материальной точки
массы
m, двигающейся по гладкой сфере радиуса R в однородном
поле тяжести.
2
2
22
1
cos
2sin
p
Hp mgR
mR
ϕ
θ
⎡⎤
⎛⎞
=++θ
⎢⎥
⎜⎟
⎜⎟
θ
⎢⎥
⎝⎠
⎣⎦
Задачи средней трудности
9.11. Составить функцию Гамильтона свободно двигающегося симмет-
ричного волчка (главные моменты инерции
J
1
, J
2
= J
1
, J
3
), используя
в качестве координат эйлеровы углы
ϕ, θ, ψ.
[]
H = p
2
θ
/2J
1
+ (p
ϕ
− p
ψ
cosθ)
2
/2J
1
sin
2
θ + p
2
ϕ
/2J
3
m
ψ
ϕ
•

Теоретическая физика. Механика (практический курс) 195
ϕ
•
x
α
9.12. Найти функцию Гамильтона и составить канонические уравнения
движения для механических систем, описанных в задачах:
а) 5.25; б) 5.30.
9.13.
Найти функцию Гамильтона ангармонического осциллятора, функ-
ция Лагранжа которого
L = x
•
2
/2 − ω
2
x
2
/2 − αx
3
+ βxx
•
2
, ω, α, β – кон-
станты.
[]
H = p
2
/[2(1 + 2βx)] + ω
2
x
2
/2 + αx
3
9.14. а) Найти уравнения движения частицы, функция Гамильтона кото-
рой имеет следующий вид:
H =
c|p|
n(p,r)
, где c – константа, а n(p,r) –
произвольная функция радиус-вектора
r и импульса частицы p.
Примечание. Данный гамильтониан описывает распространение света в
прозрачной среде с показателем преломления n. "Частицей" является
волновой пакет,
r(t) – закон его движения, r
•
– его групповая скорость, а
вектор
p, перпендикулярный волновому фронту, определяет волновой
вектор.
22
,
ccpn cpn
np
nn
⎡⎤
∂
∂
=− =
⎢⎥
∂
∂
⎣⎦
p
rp
pr
&&
б) Найти траекторию, если n(r) = ax (a – константа).
[]
x = C
1
ch(y/C
1
+ C
2
)
Задачи повышенной трудности
9.15. Треугольная призма массы М может сколь-
зить по гладкой горизонтальной плоскости.
Однородный цилиндр массы
m и радиуса r
может катиться без проскальзывания по бо-
ковой грани призмы, образующей угол
α с
горизонтом. Найти функцию Гамильтона системы, составить кано-
нические уравнения движения и решить их.
22 2
22
32()4cos
sin
23 (1sin)
xx
mr p m M p mrp p
Hmgr
mr M m
ϕϕ
⎡⎤
++ − α
⎢⎥
=−ϕα
⎡⎤
++α
⎢⎥
⎣⎦
⎣⎦

Уравнения Гамильтона. Скобки Пуассона 196
9.16. Записать функцию и уравнения Гамильтона для механических сис-
тем, описанных в задачах:
а) 5.27; б) 5.33.
9.17.
Найти функцию Лагранжа частицы, функция Гамильтона которой
имеет следующий вид
H =
c|p|
n(r)
, где c – константа, а n(r) – произ-
вольная функция радиус-вектора (см. выше задачу 9.14).
9.18.
Составить канонические уравнения пространственного движения
однородного стержня массы
m и длины 2l в однородном поле тяже-
сти. Найти первые интегралы движения.
9.19.
Найти функцию Гамильтона и составить канонические уравнения
движения двойного плоского маятника, состоящего из двух одина-
ковых стержней массы
m и длины l.

Теоретическая физика. Механика (практический курс) 197
Скобки Пуассона. Основные положения
Пусть f и g – произвольные функции обобщенных координат, импуль-
сов и времени:
f(q
1
,…,q
n
; p
1
,…,p
n
,t), g(q
1
,…,q
n
; p
1
,…,p
n
,t). Скобка Пуассона
определяется следующим образом:
{}
1
,
n
j
j
jjj
f
gfg
fg
p
qqp
=
⎛⎞
∂
∂∂∂
=−
⎜⎟
⎜⎟
∂∂ ∂∂
⎝⎠
∑
. (9.9)
Основные свойства скобок Пуассона (здесь f(q,p,t), g(q,p,t), h(q,p,t) –
функции, а
α
k
– константы)
(1) {
f, g} = −{g, f}
(
a) {f, f} = 0
(2) {
f, α} = {α, g} = 0
(3) {
∑
k
α
k
f
k
, g} =
∑
k
α
k
{f
k
, g}
(
a) {αf, g} = α{f, g}
(
b) {f
1
+ f
2
, g} = {f
1
, g} + {f
2
, g}
(4) {
∏
k
f
k
, g} =
∑
l
f
l
{
∏
k≠l
f
k
, g}
(
a) {f
1
f
2
, g} = f
1
{f
2
, g} + f
2
{f
1
, g}
(5)
∂
∂t
{f, g} = {
∂f
∂t
, g} + {f,
∂g
∂t
}
(6) {
f, {g, h}} + {h, {f, g}} + {g, {h, f}} = 0
(тождество Якоби)
Очень просто вычисляются элементарные, или
фундаментальные, скобки
Пуассона:
{q
j
, q
k
} = 0, {p
j
, p
k
} = 0, {p
j
, q
k
} = δ
jk
. (9.10)
Зачем нужны скобки Пуассона?
a
. С их помощью можно единообразным способом записать уравнения Га-
мильтона (9.2)
q
•
j
= {H, q
j
}, p
•
j
= {H, p
j
}. (9.11)
б. Для произвольной функции f(q,p,t) уравнения движения (полная произ-
водная по времени) имеют похожий вид
df
(q,p,t)
dt
=
∂f
∂t
+ {H, f}. (9.12)
Так, например, подставив вместо
f(q,p,t) гамильтониан H(q,p,t) и восполь-
зовавшись следствием
a первого свойства скобок Пуассона, мы мгновенно
Уравнения Гамильтона. Скобки Пуассона 198
получаем соотношение (9.8).
в. Если f и g – интегралы движения, то их скобка Пуассона, {f, g}, – также
интеграл движения (теорема Пуассона). В ряде случае это помогает нахо-
дить дополнительные интегралы движения и упрощает решение задач.
г. Наконец, скобка Пуассона является классическим аналогом коммутато-
ра
, играющего важную роль в квантовой механике.
Примеры решения задач
Задача 4. Вычислить скобки Пуассона:
(
а) {x, M
y
}; (б) {ϕ, ψ}, где
() ()
23 32
11
cos , sin
nn
jj jj
jj
p
qpq
==
⎡
⎤⎡ ⎤
ϕ= + ψ= +
⎢
⎥⎢ ⎥
⎢
⎥⎢ ⎥
⎣
⎦⎣ ⎦
∑∑
.
Решение. Можно сразу вычислить скобку Пуассона, "в лоб", исходя из оп-
ределения (9.9), а можно найти скобку Пуассона, используя свойства этих
скобок и постепенно сводя искомую скобку к более простым и даже из-
вестным. На примере (
а) покажем оба варианта.
(
а) В задаче предполагается 3 степени свободы: обобщенные координаты
совпадают с обычными декартовыми (
q
1
= x
1
= x, q
2
= x
2
= y, q
3
= x
3
= z),
обобщенные импульсы (
p
1
= p
x
, p
2
= p
y
, p
3
= p
z
) – с компонентами обычного
импульса. Компонента момента импульса
M
y
= [r p]
y
= M
2
= zp
x
−
xp
z
=
= x
3
p
1
−
x
1
p
3
.
I способ
– вычисление "в лоб":
{}
{}
()
33
12 12 12
12
11
3
22
131133
1
11
,,
y
jj
jj jj jj
j
j
j
xM xM xM
xM x M
px xp xp
MM
x
pxp x z
ppp
==
=
⎛⎞⎛⎞
∂∂ ∂∂ ∂∂
== − =− =
⎜⎟⎜⎟
⎜⎟⎜⎟
∂∂ ∂∂ ∂∂
⎝⎠⎝⎠
∂∂ ∂
=− δ =− =− − =− =−
∂∂∂
∑∑
∑
II способ
– использование свойств, сведение к известным скобкам.
{}
{}{ }{}{}
{}{}{}{}
(3) (4a)
12 13113 131 113
311 113 113 311 3
10 0 0
,,, , ,
,,, ,
y
xM xM xxp xp xxp xxp
x
xp pxx xxp p xx x z
=− = = =
==−= − =
= + − − =− =−
В данном случае мы свели все к фундаментальным скобкам (9.10), их зна-
чения написаны под скобками. Над знаками равенства приведены номера
Теоретическая физика. Механика (практический курс) 199
свойств, которые были применены при вычислениях. Теперь можно при
решении других задач использовать полученный результат и считать
{
x, M
y
} – "известной" скобкой Пуассона
1
.
(
б) В этой задаче главное не ошибиться при вычислении частных произ-
водных от сложных функций
ϕ(q,p) и ψ(q,p)
() ()
23 23
11 1
sin 2 2 sin
nn n
jj jjk k jj
jj j
k
p
qp p pq
p
== =
⎡⎤ ⎡⎤
∂ϕ
=− + δ =− +
⎢⎥ ⎢⎥
∂
⎢⎥ ⎢⎥
⎣⎦ ⎣⎦
∑∑ ∑
;
()
223
1
3sin
n
kjj
j
k
qpq
q
=
⎡
⎤
∂ϕ
=− +
⎢
⎥
∂
⎢
⎥
⎣
⎦
∑
;
() ()
232 32
11
3cos ; 2cos
nn
kjj kjj
jj
kk
p
pq q pq
pq
==
⎡⎤ ⎡⎤
∂ψ ∂ψ
=+=+
⎢⎥ ⎢⎥
∂∂
⎢⎥ ⎢⎥
⎣⎦ ⎣⎦
∑∑
.
Подставим их в определение (9.9), в котором поменяем индекс суммирова-
ния (
j → k)
{}
()
22 2 3
11
9
,2sin2
2
nn
kk kk j j
kj
kk kk
p
qpq pq
pq qp
==
⎡
⎤
⎛⎞
∂ϕ ∂ψ ∂ϕ ∂ψ
⎛⎞
ϕψ = − = − +
⎢
⎥
⎜⎟
⎜⎟
∂∂ ∂∂
⎝⎠
⎢
⎥
⎝⎠
⎣
⎦
∑∑
.
Задача 5. Показать, что, если функция Гамильтона зависит от переменных
q
1
и p
1
лишь опосредовано через функцию f(q
1
, p
1
), т.е.
H = H(f(q
1
, p
1
), q
2
, p
2
,…, q
n
, p
n
), то f(q
1
, p
1
) – интеграл движения.
Решение. Другими словами нужно показать, что f(q
1
,p
1
) не изменяется во
времени, т.е. является константой. С помощью скобок Пуассона решение
укладывается в одну строчку. Воспользуемся определением
2
11 11
{,} 0
n
j
jj jj
df Hf f Hf f Hf Hf
Hf
dt f p q f q p p q q p
=
⎛⎞
⎛⎞⎛⎞
∂∂ ∂ ∂∂ ∂ ∂∂ ∂∂
== ⋅− ⋅+ − =
⎜⎟
⎜⎟⎜⎟
⎜⎟
∂∂ ∂ ∂∂ ∂ ∂∂ ∂∂
⎝⎠⎝⎠
⎝⎠
∑
,
тогда первых два члена, где вычислены производные от сложной функции
H = H(f,q
2
,p
2
,…,q
n
,p
n
), отличаются только знаками, а в последней сумме
производные от
f тождественно равны 0. Отсюда следует, что
1
Из соображений симметрии, кстати, сразу следует, что {y, M
z
} = −x, {z, M
x
} = −y.

Уравнения Гамильтона. Скобки Пуассона 200
f(q
1
,p
1
) = const. Более того, очевидно обобщение этого результата, если
функция Гамильтона имеет вид
H = H(f(q
1
, p
1
,…, q
k
, p
k
,), q
k+1
, p
k+1
,…, q
n
, p
n
),
то
f(q
1
, p
1
,…, q
k
, p
k
) – интеграл движения.
Задачи
Обязательные задачи
9.20. Вычислить скобку Пуассона {ϕ, ψ}, где
а) ϕ = q
2
+ p
2
, ψ = arctg(p/q); б) ϕ = ϕ(q
2
+ p
2
), ψ = arctg(p/q);
в) ϕ = ϕ(q
2
+ p
2
), ψ = ψ(arctg(p/q)); г) ϕ = q
j
, ψ = ψ(q
1
,...,q
n
,p
1
,…,p
n
,t);
д) ϕ = p
j
, ψ = ψ(q
1
,...,q
n
,p
1
,…,p
n
,t);
е) ϕ = ϕ(q
1
,p
1
), ψ = ψ(ϕ(q
1
,p
1
),q
2
,...,q
n
,p
2
,…,p
n
,t);
ж) ϕ = ϕ(g((q
1
,...,q
n
,p
1
,…,p
n
,t)), ψ = ψ(g((q
1
,...,q
n
,p
1
,…,p
n
,t));
з)
() ()
22 22
11
cos , sin
nn
jj jj
jj
p
qpq
==
⎡⎤⎡⎤
ϕ= + ψ= +
⎢⎥⎢⎥
⎢⎥⎢⎥
⎣⎦⎣⎦
∑∑
;
и
)
() ()
23 23
11
,
nn
j
jjj
jj
p
qpq
==
⎡⎤⎡⎤
ϕ=ϕ + ψ=ψ +
⎢⎥⎢⎥
⎢⎥⎢⎥
⎣⎦⎣⎦
∑∑
.
9.21.
Вычислить скобки Пуассона:
а) {М
i
, х
j
}, б) {М
i
, p
j
}, в) {М
i
, М
j
}, г) {М
2
, М
j
},
где
х
j
, p
j
– декартовы координаты и компоненты импульса частицы,
М
j
– компоненты ее момента импульса относительно начала коор-
динат, а
М
2
= М
1
2
+ М
2
2
+ М
3
2
;
д) {(ap), (br)}, е) {(aM), (br)}, ж) {(aM), (bM)}, з) {(aM), (bp)},
где
a и b – постоянные векторы.
Примечание. При вычислениях удобно использовать элементы единично-
го антисимметричного тензора 3 ранга e
ijk
, которые обладают следую-
щими свойствами: e
ijk
= e
jki
= e
kij
=
−
e
jik
=
−
e
kji
=
−
e
ikj
. Вследствие чего эле-
менты, имеющие хотя бы 2 одинаковых индекса, обращаются в нуль.
Среди оставшиеся 6 элементов с разными индексами элементы с "пра-
вильной" последовательностью индексов равны единице, т.е.
e
123
= e
312
= e
231
= 1, а с "неправильной" – −1, т.е. e
213
= e
321
= e
132
= −1. С
