Леушин А.М., Нигматуллин Р.Р., Прошин Ю.Н. Теоретическая механика (практический курс). Задачник для физиков

Подождите немного. Документ загружается.

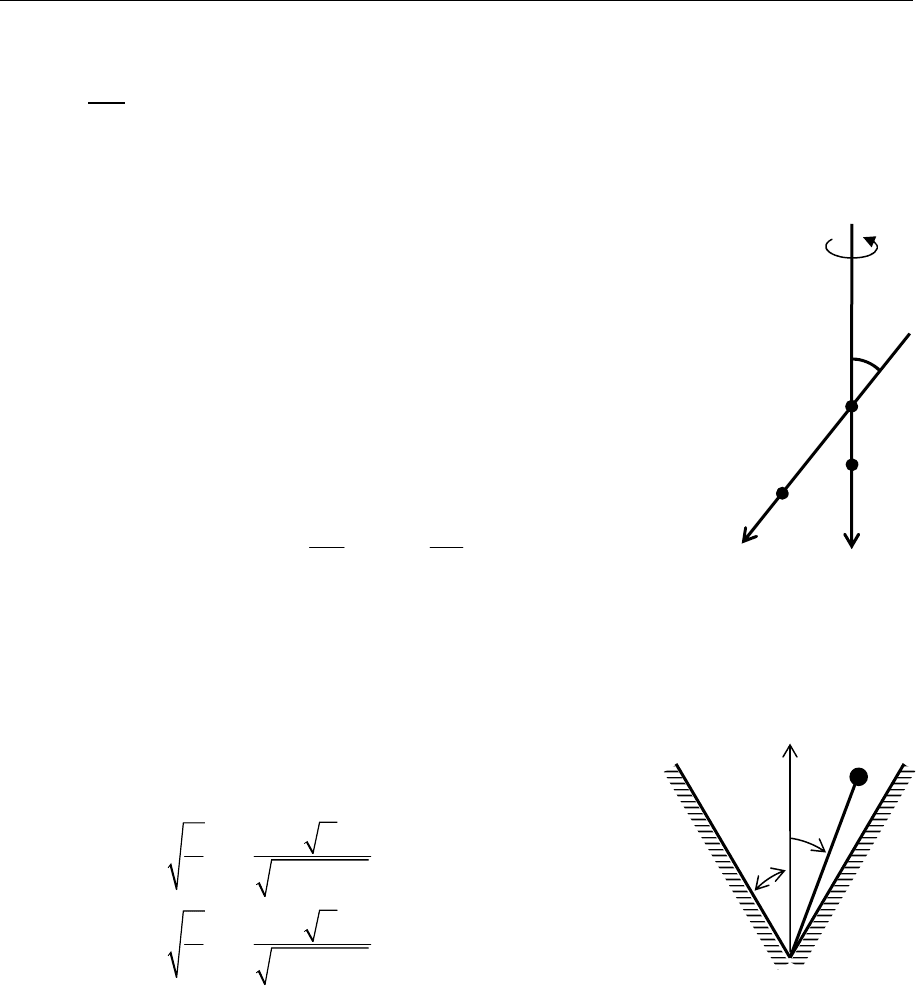
Теоретическая физика. Механика (практический курс) 181

имеют длину l

, а пружина, соединяющая шарики – длину l

. Найти

все

точки равновесия и собственные частоты системы.

8.31.

Система, состоящая из двух жестко связанных стержней Ox и Oy,

образующих угол α = π/3, вращается с постоянной угловой скоро-

стью Ω вокруг вертикального стержня Oy. По каж-

дому из стержней может двигаться без трения ко-

лечко массы m. Колечки притягиваются друг к дру-

гу с силой, пропорциональной расстоянию между

ними (коэффициент пропорциональности

a = 9mΩ

/5). Найти малые колебания системы в ок-

рестности положения устойчивого равновесия.

⎡⎤

ω= ω=

⎢⎥

⎣⎦

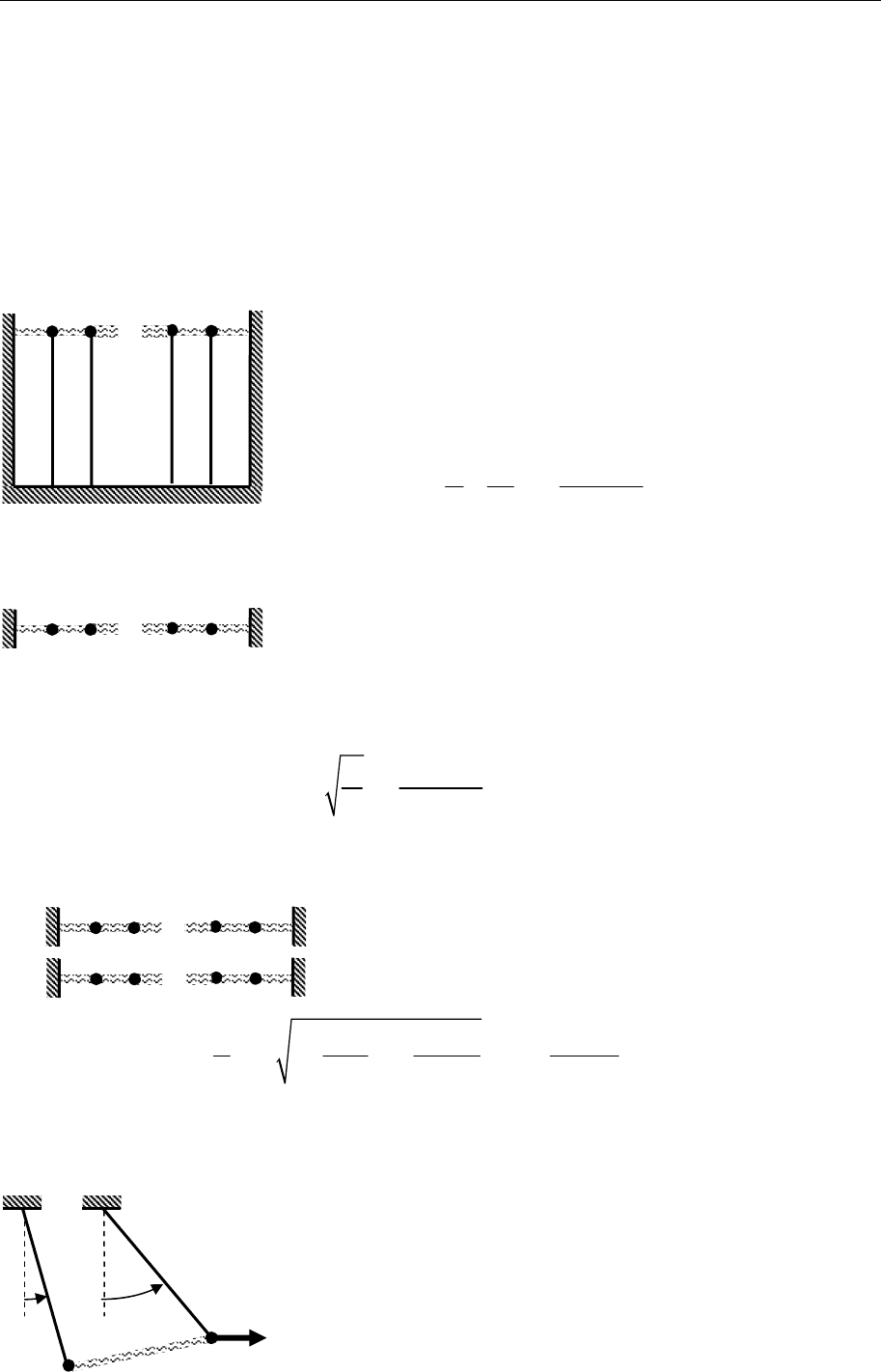
8.32. Обращенный математический маятник (см. рисунок) массы m и

длины l может совершать колебания между преградами, образую-

щими с вертикалью Oz малый угол 2α. Считая удар о преграду аб-

солютно упругим, найти приближенное значе-

ние периода T колебаний маятника.

4arsh ,при

2arsh ,при

Tlg

⎡⎤

=ϕ>ϕ

⎢⎥

ϕ−ϕ

⎢⎥

=ϕ<ϕ

⎢⎥

ϕ−ϕ

⎣⎦

8.33. Найти частоту малых колебаний системы в задаче 8.7 для более

сложных случаев:

а) a = b = l, m

≠ m

; б) a ≠ b, m

= m

= m;

в) a ≠ b, m

≠ m

(общий случай).

8.34.

Определить нормальные частоты и координаты системы в задаче

8.23 для более сложных случаев:

а) m

= m

= m, c

= с

= 2с

= 2с;

б) m

= 3m

= 3m, c

= с

= 2с

= 2с;

в) m

≠ m

, c

= с

= 2с; г) m

≠ m

, c

≠ с

≠ c

Малые колебания механических систем 182

1 2

…

F(t)

8.35. Однородная горизонтальная прямоугольная тонкая пластинка со

сторонами а и b опирается своими углами на четыре одинаковые

пружины жесткости с. Предполагая, что масса пластины равна М,

определить частоты ее свободных колебаний.

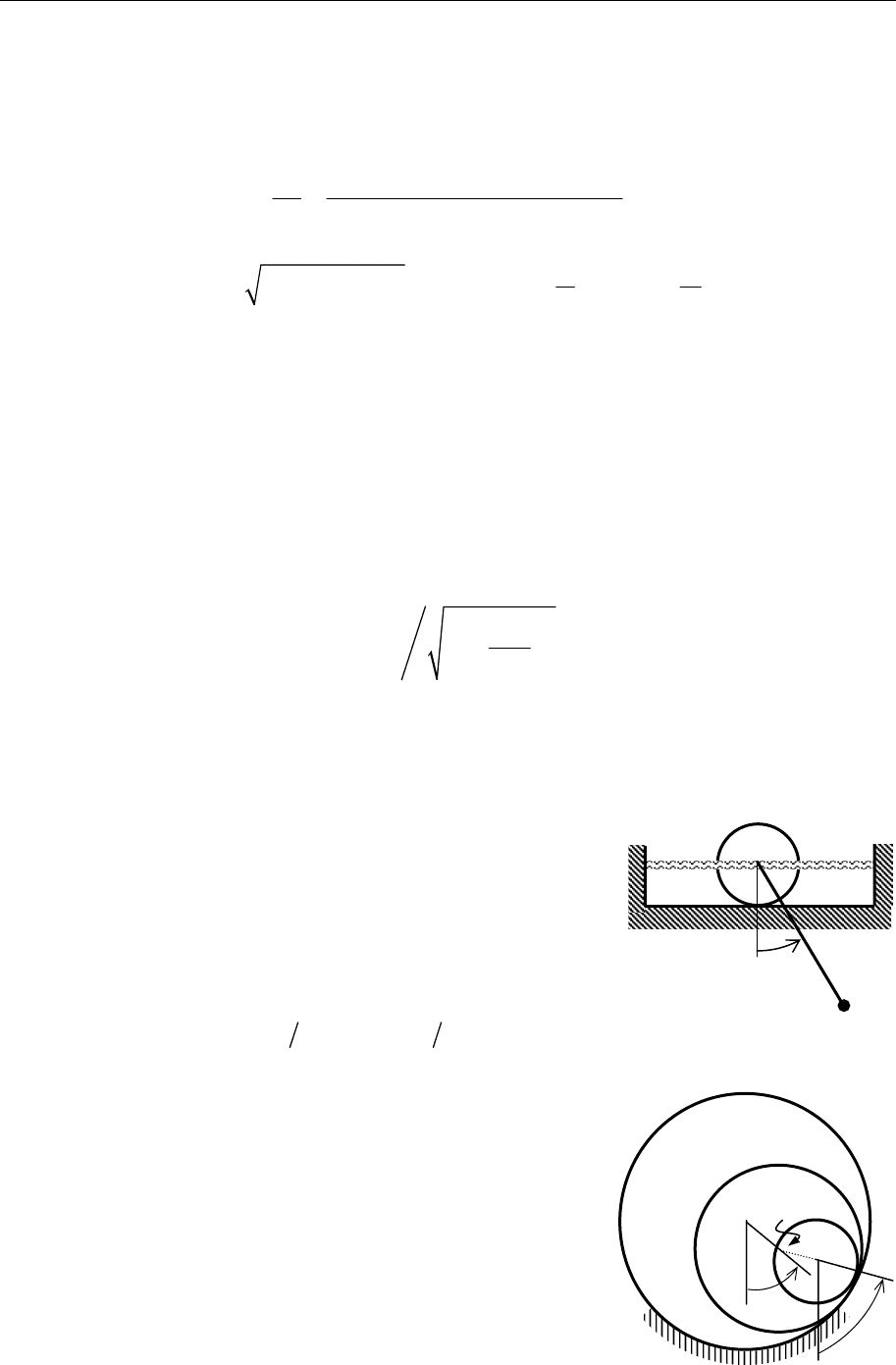
8.36.

Найти собственные частоты колебаний системы маятников, изо-

браженной на рисунке. Массы всех шариков равны m, длины всех

стержней – l, и все пружины имеют одну и ту же

жесткость, равную с. Допустить, что углы откло-

нений стержней от вертикали подчиняются гра-

ничному условию φ

= φ

N + 1

= 0.

sin , 1, 2,...,

2( 1)

gc n

lm N

⎡

⎤

ω=− + =

⎢

⎥

⎣

⎦

8.37. Найти закон дисперсии системы N частиц массой m, двигающихся

вдоль горизонтальной прямой и соединенных ме-

жду собой и с неподвижными стенками пружина-

ми жесткости c, предполагая, что отклонения частиц от положений

равновесия подчиняются граничным условиям x

= x

N+1

= 0.

2 sin , 1,2,...,

2( 1)

⎡⎤

ω= =

⎢⎥

⎣⎦

8.38. Найти закон дисперсии: а) системы 2N частиц с массами m и M, со-

единенных пружинами жесткости с; б) системы

2N частиц с массами m, соединенных пружина-

ми жесткости c

и c

, как показано на рисунке.

1,2

) 1 1 sin , ; 1, 2,...,

cnmM

а nN

mM N m M

⎡⎤

⎛⎞

μπ

⎢⎥

⎜⎟

ω= ± − μ= =

⎜⎟

μ++

⎢⎥

⎝⎠

⎣⎦

8.39. Два одинаковых маятника массы m и длины l соединены пружиной

жесткости c (длина пружины в ненапряженном

состоянии l

). К одному из них приложена сила

F(t) = F

sinΩt, направленная по горизонтали. Ис-

следовать зависимость амплитуд линейных коле-

баний маятников A

(i = 1,2) от частоты внешней

1 2

…

)

m m

Теоретическая физика. Механика (практический курс) 183

силы Ω (рассмотреть также предельные случаи очень большой и

очень малой частоты Ω по сравнению с другими характерными час-

тотами задачи).

()

112

22 2 22

21 пруж

22 2 22 2

1 маят пруж 2 маят пруж

2; =; =

⎡⎤

ω−ω

⎢⎥

ω−ω−Ω +Ωω

⎢⎥

ω= ω +ω ω=ω ω

⎢⎥

⎣⎦

8.40. Решить задачу о малых колебаниях системы, описанной в задаче

7.37.

8.41.

Собственная частота линейного осциллятора без затухания равна

. Найти частоту затухающих колебаний этого же осциллятора в

среде с сопротивлением, пропорциональным скорости, если за n ко-

лебаний его амплитуда уменьшается в k раз.

⎡⎤

⎛⎞

⎢⎥

ω=ω +

⎜⎟

⎢⎥

⎝⎠

⎣⎦

8.42. Однородный диск радиуса R и массы m

= m, центр которого соеди-

нен с неподвижными стенками двумя одинаковыми пружинами же-

сткости c каждая, может без проскальзыва-

ния катиться по горизонтальной прямой. К

центру диска подвешен математический ма-

ятник длины l и массы m

= m/2. Считая, что

cl = mg, найти малые колебания системы.

23, 2gl gl

⎡⎤

ω= ω=

⎣⎦

8.43. Три цилиндрические трубы с радиусами

= 3r, R

= 2r, R

= r вложены одна в

другую, как показано на рисунке. Внеш-

няя труба радиуса R

неподвижна, про-

скальзывание меду трубами отсутствует, а

их массы равны соответственно m

= 3m,

= m. Найти малые колебания системы около положения устойчи-

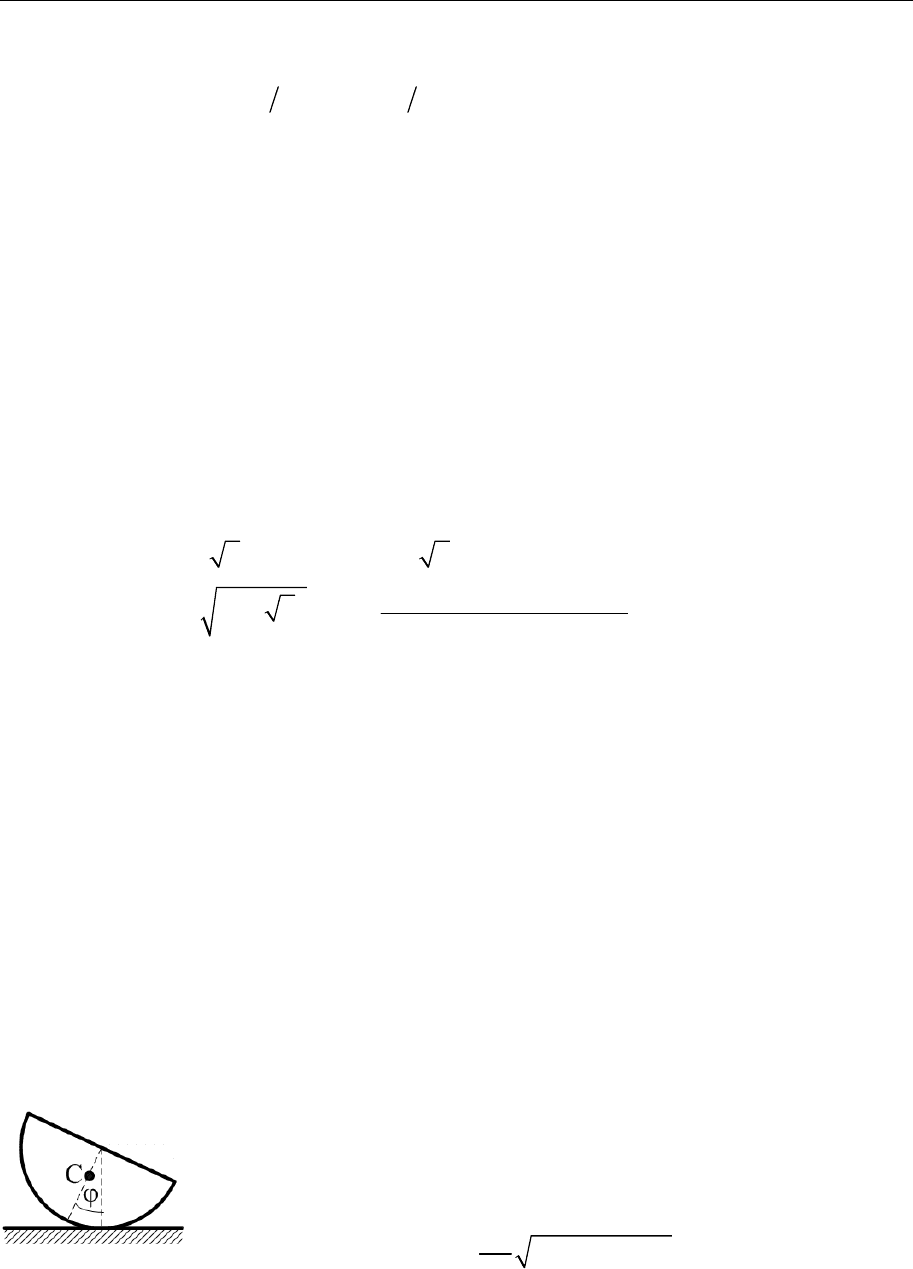
Малые колебания механических систем 184

вого равновесия.

3,gr gr

⎡⎤

ω= ω=

⎣⎦

8.44. Параметры системы, описанной в задаче 8.18, удовлетворяют усло-

виям M = m и 2mg = cl, а к ползуну приложена горизонтальная сила

(t) = F

sinΩt.

а) Найти малые колебания системы

б) Определить ненулевую частоту воздействия Ω и начальные зна-

чения х

, x

•

, ϕ

•

, при которых ползун во время движения будет

неподвижен. Найти закон изменения ϕ(t).

()()

()

() ()

()

1112 22

111 2 22

1,2

2224

) sin sin sin

2 sin 2 sin sin

22; ; , константы

axC t C t Agl t

lCt CtAlt

mg gl l

⎡⎤

⎢⎥

=ω+φ+ω+φ+−ΩΩ

⎢⎥

ϕ=− ω +φ + ω +φ − Ω Ω

⎢⎥

ω= ± = φ−

⎢⎥

−Ω+Ω

⎢⎥

⎣⎦

8.45. Решить задачу о малых колебаниях механической системы, описан-

ной в задаче 5.25 при следующих значениях параметров

а) m

= m

= m, c

= с

= с;

б) m

= m

= 2m

= 2m, 2c

= с

= 2с;

в) Рассмотреть предельные случаи, когда одна из масс обраща-

ется в бесконечность, а другие массы равны между собой.

8.46.

Определить влияние, оказываемое вращением Земли, на малые ко-

лебания маятника (так называемый маятник Фуко).

8.47.

Определить период малых колебаний однородного полукруглого

диска радиуса R, находящегося на негладкой горизон-

тальной плоскости, по которой он может катиться без

скольжения.

2 (9 16)

TgR

⎡

⎤

=−

⎢

⎥

⎣

⎦

Теоретическая физика. Механика (практический курс) 185

Уравнения Гамильтона. Скобки Пуассона

Раздел 9. Уравнения Гамильтона.

Скобки Пуассо

на.

Уравнения Га

мильтона. Основные положения и формулы

Для механической системы с n степенями свободы существуют урав-

нения Лагранжа (5.15): n

дифференциальных уравнений второго порядка,

содержащие q

••

, q

•

и q

. Свойства механической системы заложены в функ-

ции Лагранжа L(q,q

•

,t) = T − U, зависящей от n независимых переменных:

обобщенных координат q(q

,…,q

), а обобщенный импульс p

определя-

ется соотношением

∂L

∂

•

. (9.1)

Гамильтонов формализм классической механики

связан с введением 2n

независимых обобщенных переменных: к обобщенным координатам до-

бавлено n обобщенных импульсов p(p

,…,p

). Свойства механической

системы заложены в

функции Гамильтона

H(q,p,t) – обобщенной энер-

гии системы. Движение механической системы в отсутствие диссипатив-

ных сил можно определить, решив соответствующие

уравнения Гамиль-

тона

: систему 2n дифференциальных уравнений первого порядка

∂

⎧

=−

⎪

∂

⎪

⎨

∂

⎪

∂

⎩

(j = 1,2,…,n). (9.2)

Для аналитического решения в случае простых систем лагранжев подход часто оказывается

более удобным. Однако в более сложных случаях – при переходе к квантовой механике, в

статистической механике, при численном решении уравнений и т.д. – предпочтителен га-

мильтонов формализм.

Часто функцию Гамильтона, особенно в квантовой механике, называют гамильтонианом.

Уравнения Гамильтона. Скобки Пуассона 186

Окончательно, с учетом 2n начальных условий (q

) можно записать за-

кон движения данной системы как q

= q

,t) и p

= p

,t), где

j = 1,2,…,n. Уравнения Гамильтона в записи (9.2) иногда называют

кано-

ническими уравнениями движения

Таким образом, для решения уравнений движения в гамильтоновом

формализме (9.2) необходимо определить процедуру нахождения функции

Гамильтона для любой механической системы.

Покажем, как можно найти функцию Гамильтона, зная

функцию Ла-

гранжа. Проще всего воспользоваться определением обобщенной энергии

системы H (см. также замечание к задаче 5 на странице 91)

12 1 2 12 12

( , ,..., ; , ,..., , ) ( , ,..., ; , ,..., , )

nnjj nn

qq q p p pt pq Lqq q qq qt

=−

∑

&&&&

. (9.3)

Справа в этом выражении присутствуют как "нужные" переменные q,p,t,

так и "лишние" переменные q

•

. Чтобы найти, как эти "лишние" обобщен-

ные скорости выражаются через "нужные" переменные, т.е. q

•

= q

•

(q,p,t),

необходимо воспользоваться определением (9.1)

12 12

(,,)

( , ,..., ; , ,..., , )

jjnn

pqq qqq qt

∂

&& &

(j = 1,2,…,n). (9.4)

и решить полученную систему алгебраических уравнений относительно q

•

После чего осталось подставить найденные соотношения q

•

= q

•

(q,p,t) в вы-

ражение (9.3), привести подобные члены и получить искомую функцию

Гамильтона.

Иногда возникает необходимость в решении обратной задачи, в нахо-

ждении функции Лагранжа по известной функции Гамильтона. Для этого

воспользуется (9.3)

12 12 12 1 2

( , ,..., ; , ,..., , ) ( , ,..., ; , ,..., , )

nnjj n n

qq q qq qt pq Hqq q pp pt

=−

∑

&& & &

, (9.5)

а "лишние" p

как функции "нужных" переменных p

(q,q

•

,t) найдем из сис-

темы алгебраических уравнений (см. второе выражение в (9.2))

12 1 2

(;,)

( , ,..., ; , ,..., , )

jjnn

qqqqqpppt

∂

(j = 1,2,…,n). (9.6)

Теоретическая физика. Механика (практический курс) 187

Подставим найденные импульсы p

(q,q

•

,t) в (9.5) и, после приведения по-

добных слагаемых, получим функцию Гамильтона.

Циклические переменные в гамильтоновом формализме

Если какая-либо обобщенная переменная (например, q

) не входит яв-

ным образом в функцию Гамильтона, т.е. является циклической коорди-

натой

, то соответствующий этой координате

обобщенный импульс p

яв-

ляется интегралом движения

, т.е. не меняется со временем.

Действительно, пусть H(q

,…,q

k−1

k+1

,…,q

; p

,…,p

k−1

k+1

,…,p

,t),

тогда это напрямую следует из уравнений Гамильтона (см. первое выраже-

ние в (9.2))

111 1

(,, , ,,; ,,;)

0const

kk n n

k k

Hq q q q p p t

−+

∂

=− ≡ → =

∂

KKK

. (9.7)

Циклической

переменной может быть и время t, т.е. H(q

, …,q

,…,p

). В

этом случае в отсутствие диссипативных сил сохраняется

обобщенная

энергия, т.е. функция Гамильтона

H(q

, …, q

, p

,…, p

) = const, и механи-

ческая система является обобщенно-консервативной. Как мы видим, нали-

чие циклических переменных упрощает решение уравнений Гамильтона.

Напомним также, что обобщенную энергию H можно записать как

(2) (0)

TUT

+− (9.8)

(см. (5.19) и (5.20)). Отсюда видно, что, если на систему наложены только

стационарные связи, то обобщенная энергия совпадает с обычной полной

энергией системы:

(2)

TUTUE=+=+=.

В общем же случае, при наличии диссипативных

Q либо других непо-

тенциальных сил

нп

Q первые n уравнений Гамильтона (9.2) приобретут вид

нп

∂

=− +

∂

Напомним, что циклическая координата не будет явно содержаться и в функции Лагранжа

(см. замечание к задаче 5 на странице 91).

Часто говорят "сопряженный этой координате" импульс, а q

, p

называют сопряженными

переменными (

j – любое).

Уравнения Гамильтона. Скобки Пуассона 188

а закон изменения обобщенной энергии системы записывается так

( ,..., , ,..., , )

dH H q q p p t

dt t

∂

, (9.8)

где

NQq

∑

– мощность диссипативных сил.

Примеры решения задач

Задача 1. Найти функцию Гамильтона и провести анализ движения систе-

мы в гамильтоновом формализме для простейших механических систем:

a) свободной частицы; б) гармонического осциллятора;

в) частицы в центральном поле.

Решение. Действуем по алгоритму:

9 сначала находим функцию Лагранжа L(q,q

•

,t) = T(q,q

•

,t) − U(q,t)

(

для данных систем функция Лагранжа найдена в задаче 5 из раздела 5),

9 затем выражаем с помощью (9.4) обобщенные скорости через коор-

динаты и импульсы,

9 эти выражения подставляем в определение (9.3).

а) Функция Лагранжа свободной частицы в декартовых координатах име-

ет вид

222

(/2)( )

mxyz=++

(число степеней свободы n = 3 и q

= x, q

= y,

= z). Находим соответствующие обобщенные импульсы

, ,

xyz

LLL

mx p my p mz

xyz

∂∂∂

== == ==

∂∂∂

(обобщенные импульсы совпадают с обычными, кинематическими им-

пульсами

!), следовательно, x

•

= p

/m, y

•

= p

/m, z

•

= p

/m. Подставляем полу-

ченные скорости в определение функции Гамильтона (9.3)

222

222 222

(, ,, , , ) ( /2)( )

()/()/(2)

xyz x y z

xyz

xyz xyz

Hxyzp p p xp yp zp m x y z

ppp

pppmppp m

=++− ++=

=++ −++ = =

&& &&

В общем случае размерность обобщенных импульсов может не совпадать с размерностью ки-

нематических импульсов (см., например, ниже

ниже в пункте в данной задачи).

Теоретическая физика. Механика (практический курс) 189

Допустима векторная запись:

L = mv

/2 = m(vv)/2 = m(r

•

)/2 →

p = ∂L/∂r

•

= mr

•

→ r

•

= p/m →

→ H(

r,p) = (pr

•

) − mr

•

/2 = p

/m − p

/2m = p

/2m.

Поскольку в гамильтониан координаты вообще не входят, то все компонен-

ты импульса – интегралы движения. Уравнения Гамильтона (9.2) приобре-

тают вид

•

= −∂H/∂r = 0 и r

•

= ∂H/∂p = p/m. Решения – p = p

, r = p

t/m + r

б) Функция Лагранжа одномерного линейного гармонического осциллято-

ра L(x,x

•

) = mx

•

/2 − mω

/2. Следовательно, p = ∂L/∂x

•

= mx

•

и x

•

= p/m. Тогда

функция Гамильтона

H(x,p) = px

•

(p) − L(x,x

•

(p)) = p

/2m + mω

и она совпадает с полной энергией гармонического осциллятора E. Запись

уравнений движения в гамильтоновом формализме также элементарно

•

= −∂H/∂x = −mω

x, x

•

= ∂H/∂p = p/m.

После дифференцирования по времени второго уравнения и подстановки p

•

в первое, мы имеем стандартное уравнение гармонического осциллятора

••

+ ω

x = 0

с известным решением (см., например, раздел 8).

в) Лагранжиан частицы в центральном поле (две степени свободы: q

= ρ,

= ϕ – полярная система координат): L(ρ,ϕ,ρ

•

,ϕ

•

) = mρ

•

/2 + mρ

•

/2−U(ρ).

Попутно замечаем, что ϕ является циклической координатой в лагранже-

вом формализме, поскольку не входит в явном виде в функцию Лагранжа.

Обобщенные импульсы, сопряженные координатам ρ и ϕ соответственно:

pmpm

ρϕ

∂∂

==ρ ==ρϕ

∂ρ ∂ϕ

Выражаем обобщенные скорости через импульсы и координаты

ρ= ϕ=

Уравнения Гамильтона. Скобки Пуассона 190

Эти выражения подставляем в определение функции Гамильтона (9.3) и

решаем задачу, находя H = H(ρ,ϕ,p

222

() ()

22 2

pp p p pp

Hp p U U

mm m

mmm

ρϕ ρ ϕ ρϕ

ρϕ

⎛⎞ ⎛ ⎞

= + − − +ρ= + +ρ

⎜⎟ ⎜ ⎟

ρρρ

⎝⎠ ⎝ ⎠

Подчеркнем, что ϕ является циклической

координатой и в гамильтоновом

формализме

. Это означает, что соответствующий обобщенный импульс p

(физический смысл: z-компонента момента импульса M

!) является инте-

гралом движения, что напрямую следует из уравнений Гамильтона и за-

метно упрощает их решение

0const;

;

ppp p

pp p

ppm

ϕϕϕ ρ

ϕϕ ρ

ϕρ

∂∂∂

=− = → = = =− = −

∂ϕ ∂ρ ∂ρ

∂∂

ϕ= = = ρ= =

∂∂

ρρ

Во всех рассмотренных выше случаях (а-в) циклической

переменной

является также и время

, что приводит к сохранению обобщенной энергии

(функции Гамильтона) H(

q,p) = E = const, что в данном случае (в отличие

от случаев а, б) действительно упрощает решение уравнений движения.

После подстановок получаем известное уравнение, используемое для ана-

лиза движения частицы в центральном поле (см. раздел 3),

()

⎡

⎤

ρ= − ρ−

⎢

⎥

⎢

⎥

⎣

⎦

Задача 2. Найти функцию Гамильтона и написать канонические уравнения

движения системы, функция Лагранжа которой имеет следующий вид

() ()

()

222 22

112 13 1 2 312

qqqqq qqqqq=++−+++

&&&&

Решение. Система имеет три степени свободы. Сначала используем опре-

деление обобщенных импульсов (9.4) и найдем q

•

= q

•

(q,p,t) = q

•

(q,p)

(j = 1,2,3)

См. замечание на странице 91.