Лекции по механике разрушения
Подождите немного. Документ загружается.

Схема построена на основании опытов, проводившихся на каменной соли, и
относится либо к однородному напряженному состоянию, либо к элементу объема.
Такие важнейшие факторы, как вид напряженного состояния и существование у
одного и того же материала двух физически различных сопротивлений разрушению,
в этой схеме вовсе не отражены. Хотя схема Иоффе построена в координатах
напряжение – температура испытания, а схема Людвика в координатах напряжение
– деформация (при различных скоростях деформации), по сути дела в обоих схемах
выражена одна и та же идея – материал имеет практически не изменяющееся (от
температуры в схеме Иоффе или от скорости в схеме Людвика) сопротивление
разрушению (отрыву) и сильно изменяющееся от тех же факторов сопротивление
пластической деформации, которое характеризуется в схеме Иоффе пределом
текучести, а в схеме Людвика – текущими ординатами кривой деформации).
Схема А.Ф.Иоффе сыграла важную роль в понимании механических свойств, в
особенности при изучении хладноломкости металлов в работах Н.Н.Давиденкова и
его школы. Применение и развитие этой схемы для металлов принадлежит
Н.Н.Давиденкову. Он отмечал, что одни металлы являются хладноломкими, т.е.
разрушаются хрупко при понижении температуры, а другие нет. Потеря
пластичности и переход в хрупкое состояние при определенной критической
температуре (или в интервале температур) свойственны не всем металлам. С одной
стороны, малоуглеродистые стали, цинк, кадмий, магний, подвержены
хладноломкости, с другой стороны, медь, алюминий, никель, свинец, аустенитные
стали даже при испытании на ударный изгиб с надрезом при низких температурах
не теряют своей пластичности. Можно предположить, что различное поведение
зависит от типа кристаллической решетки и что решетки объемноцентрированного
куба и гексагональная склонны к хладноломкости, а решетка гранецентрированного
куба ее не обнаруживает. Для металлов с решеткой объемноцентрированного куба и
гексагональной повышение диаграммы сжатия, главным образом, вызывается одним
охлаждением и проявляется в повышении предела текучести, тогда как для металлов
с решеткой гранецентрированного куба следствием понижения температуры
является повышение коэффициента упрочнения. При этом повышение предела
текучести у первых металлов при растяжении может привести к хрупкому
разрушению, если только предел текучести поднимется выше сопротивления
отрыву (по схеме А.Ф.Иоффе). Напротив, для второй группы металлов
сопротивление отрыву при наличии растягивающих напряжений могло бы быть
достигнуто (впрочем, никогда не достигается) только после определенной степени
пластической деформации, поэтому совершенно хрупкое разрушение невозможно.
Схема Н.Н.Давиденкова (1936 г.)(рис.27). Основываясь на результатах
исследования монокристаллов -железа, которые в зависимости от температуры и
других условий опыта могут разрушаться пластичски, по плоскостям, проходящим
через диагональ куба, и хрупко по граням куба, было предложено учитывать не
только два вида разрушения, но и два сопротивления разрушению, названные
Давиденковым вязким и хрупким отрывом.
41

Рис. 27. Схема Н.Н.Давиденкова.
Кривая CL – сопротивление хрупкому разрушению,
MB – сопротивление вязкому разрушению.
Введенные Давиденковым в схему механического состояния две различные
ветви разрушения положили начало разграничению между характеристиками
разрушения – сопротивлением отрыву и сопротивлением срезу. В дальнейшем
выяснилось, что каждая из этих характеристик связана с различными по характеру
напряжениями: сопротивление отрыву с растягивающими, сопротивление срезу с
касательными. На схеме наносится семейство истинных кривых деформирования
для различных напряженных состояний. Концевые точки кривых (соответствующие
разрушению) располагаются на ветви CL – хрупких разрушений и ветви MB –
вязких разрушений.
Схема перехода из вязкого в хрупкое состояние (рис. 28), предложенная
Е.М.Шевандиным (1953 г.), состоит из кривых истинных напряжений s=f(),
полученных при температуре испытания от +20 до –196
0
С для сталей, склонных к
хрупкому разрушению. Схема похожа на схему Н.Н.Давиденкова, однако кривая,
огибающая конечные точки кривых истинных напряжений, состоит не из двух
ветвей, как у Давиденкова, а из трех. Ветвь DC определяет область вязких
разрушений с изломами волокнистого строения, ветвь CB – область полухрупких
смешанных разрушений с изломами частично кристаллического строения, ветвь BA
– хрупкие разрушения с изломами кристаллического строения.
Рис. 28. Схема Е.М.Шевандина
Во всех этих схемах не отражено влияние одного из наиболее важных (если не
самого важного) факторов: напряженного состояния, которое оказывает огромное
влияние на механические свойства.
Различными авторами был предложен ряд схем (рис. 29-34), в которых в
отличие от описанных схем учтено также и напряженное состояние, причем в
42
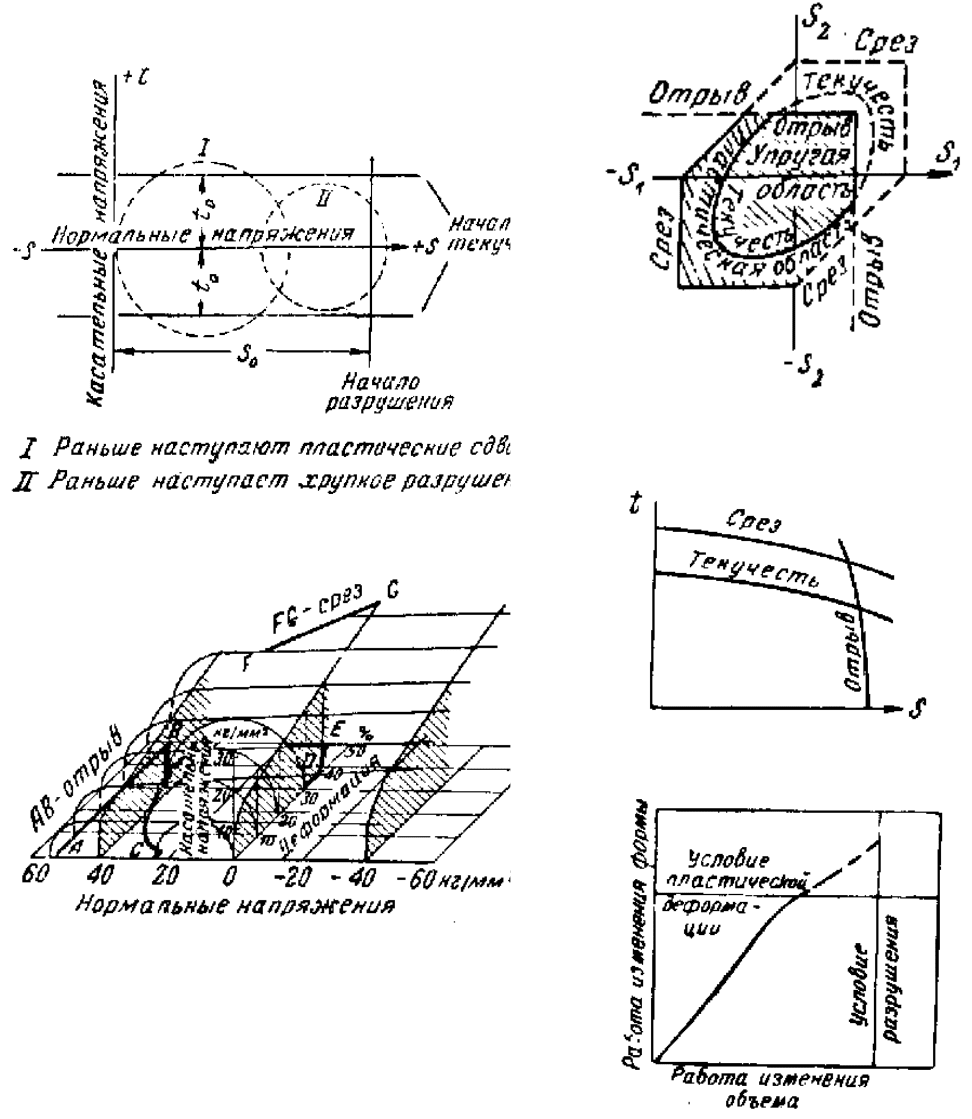
большинстве этих схем принято, что разрушение путем отрыва описывается I, а
путем среза – III теорией прочности.
Рис. 29. Схема П.Людвика (1929 г.)
Рис. 30. Схема Э.Зибеля (1932 г.)
Рис. 31. Схема Г.Фромма (1931 г.)
Рис. 32. Схема А.И.Дымова (1933 г.)
Рис. 33. Схема М.Генсамера (1941 г.)
43
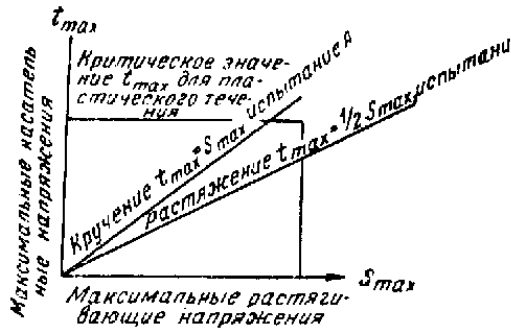
Рис. 34. Схема Н.Ф.Лашко (1951 г.)
В качестве основы для расчетов прочности при сложном напряженном
состоянии предлагались различные принципы, обычно называемые теориями
прочности. Неоднократно делавшиеся попытки применить ко всем материалам при
различных напряженных состояниях какую-либо одну теорию неизменно кончались
неудачей, т.к. I теория оказывалась неудовлетворительной для пластичных
материалов, а III – для хрупких. Поэтому было предложено разграничить выбор
теорий прочности в зависимости от свойств материалов, а именно: для хрупких
материалов (чугун, бетон и т.п.) применять I и II, а для пластичных (большинство
металлов) – III и IV теории.
Однако в настоящее время можно считать установленным, что хрупкость и
пластичность – состояния, в которые при определенных условиях может быть
переведено большинство материалов (например, чугун может быть пластически
деформирован при сжатии, а многие стали из пластичных становятся хрупкими при
переходе от кручения к растяжению). Отсюда, естественно, вытекает, что для
одного и того же материала, в зависимости от того, находится ли он в хрупком или в
пластическом состоянии, должны применяться разные теории прочности. Поэтому
можно говорить о синтезе теорий прочности, которые отражают различные виды
нарушения прочности.
В качестве приближенного графического отображения такого синтеза
Я.Б.Фридманом было предложено построение диаграммы механического состояния
(рис. 35), оценивающей поведение материала при однократных кратковременных
статических нагружениях.
Диаграмма механического состояния Фридмана. Диаграмма учитывает (рис.
35)
1. Напряженное состояние, приближенно характеризуемым отношением =t
max
/
S
n
max
;
а) если t
max
>> S
n
max
, т.е. касательные напряжения создаются при очень малых
удлинениях, то способ нагружения является мягким (например, испытание на
твердость при вдавливании, осевое сжатие под гидростатическим давлением и т.п.);
б) если t
max
<< S
n
max
, т.е. создаются значительные упругие удлинения при малых
касательных напряжениях, то способ нагружения является жестким (например,
трехосное растяжение, возникающее во внутренних слоях растягиваемого
надрезанного образца, в меньшей мере изгиб и растяжение);
44
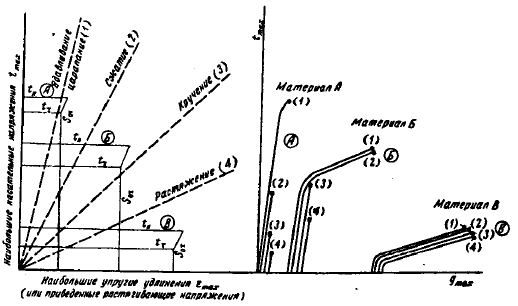
в) наконец, если t
max
S
n
max
, то способ нагружения является средним по своей
жесткости (например, кручение цилиндрического стержня, при котором при =0.25
t
max
/S
n
max
= 0.8).
Рис. 35. Диаграмма механического состояния Я.Б.Фридмана
Величина не может исчерпывающе характеризовать вид нагружения.
Назначение этой величины в том, чтобы дать сравнительную оценку опасностей
двух видов нарушения прочности: от касательных напряжений (текучесть или срез)
и от растягивающих (отрыв). При этом предполагается, что эти нарушения
прочности определяются величинами t
max
и S
max
.
2. Отношение сопротивления отрыву S
от
к сопротивлению срезу t
к
:
а) если S
от
<< t
к
, то материал при многих способах нагружения будет склонен к
разрушению путем отрыва, как правило, хрупкому (стекла, горные породы, чугуны,
твердые сплавы, пластмассы); такие материалы обычно значительно менее прочны
при растяжении, чем при сжатии;
б) если S
от
>> t
к
, то материал при многих способах нагружения будет склонен к
разрушению путем среза, как прпавило, пластичному (алюминий, медь, свинец,
многие железные сплавы);
в) если S
от
t
к
,, то материал при близких нормальных и касательных
напряжениях будет примерно в равной степени склонен к обоим видам разрушения.
3. Разное для разных способов нагружения положение сопротивления отрыву по
отношению к обобщенной кривой.
Диаграмма механического состояния составляется из двух расположенных
рядом частей. По оси ординат обеих частей диаграммы отложены максимальные
касательные напряжения t
max
. По оси абсцисс отложены в левой части максимальные
приведенные растягивающие напряжения S
n
max
, в правой – максимальные
пластические сдвиги g
max
. Левая часть диаграммы характеризует условно жесткость
или мягкость способа нагружения, в то время как правая часть диаграммы
представляет собой просто обобщенную кривую течения.
Какой-либо способ нагружения (в данной точке тела) изображен в левой части
диаграммы лучом, имеющим определенный угол наклона. Кроме того, в левой части
нанесены прямыми линиями: предел текучести t
т
, сопротивление срезу t
к
,
выраженные в касательных напряжениях, и сопротивление отрыву S
n
от
, - в
приведенных напряжениях.
45
Если условия нагружения таковы, что равенство t
max
= t
к
будет осуществлено
раньше, чем S
n
max
= S
n
от
, то произойдет разрушение путем среза. В этом случае по
мере повышения касательного напряжения от t
max
= t
т
(переход в пластическую
область) до t
max
= t
к
(срез) будет полностью “использована” обобщенная кривая
течения данного материала. Если же еще до того, как будет достигнуто условие t
max
=
t
к
, осуществится условие S
n
max
>= S
n
от
, то материал разрушится путем отрыва и
кривая t
max
=f(g
max
) “преждевременно” оборвется; пластичность g
max
и вязкость
(пропорциональная площади кривой) окажутся пониженными, причем степень этой
“преждевременности” будет тем большей, чем больше S
n
max
/ t
max
.
Конечно, если материал столь хрупок, что t
т
= t
к
, то никаким изменением
способа нагружения (при данной скорости и температуре деформации) его нельзя
перевести в пластичное состояние и кривая t
max
=f(g
max
) у него отсутствует.
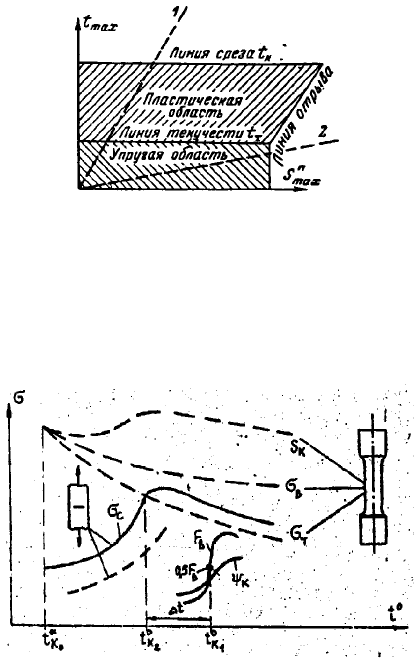
Таким образом, на диаграмме механического состояния прямые t
т
, t
к
и S
от
ограничивают две замкнутые области (рис. 36):
а) упругую область, ограниченную линиями t
т
(переход в пластическую
область), и S
от
(переход к хрупкому отрыву без пересечения пластической области,
т.е. при t < t
т
).Нижняя часть вертикальной линии S
от
ограничивает хрупкое
состояние, т.е. отрыв без предшествующей пластической деформации;
б) пластическую область, ограниченную линиями t
к
(разрушение путем среза) и
S
от
(не вполне хрупкое разрушение путем отрыва). В последнем случае отрыв
происходит уже после более или менее значительной пластической деформации,
которая оказывает сильное влияние на величину сопротивления отрыву.
Рис. 36. Схема, показывающая области упругой
и пластической деформации на диаграмме механического состояния
Широко известны температурные зависимости механических свойств и
характера разрушения (рис. 37).
Рис. 37. Зависимость механических свойств от температуры
46
С понижением температур большинство малоуглеродистых и
низколегированных сталей изменяет свои механические свойства. Точка
пересечения кривых предела текучести и сопротивления отрыву определяет
критическую температуру хрупкости согласно схеме Иоффе. С понижением
температуры предел текучести и временное сопротивление повышается, а
пластичность падает.
По температурным зависимостям характеристик разрушения образца с
трещиной можно выделить две критические температуры: первую, при 50% вязкого
составляющего в изломе, и вторую, характеризующуюся точкой пересечения
разрушающего напряжения и предела текучести. Принято считать, что при
температурах выше первой критической возникают вязкие разрушения, при
температурах ниже второй критической – хрупкие, в промежутке между
критическими температурами – квазихрупкие разрушения.
9. Сингулярные задачи теории упругости для тел с
трещинами
Основным модельным представлением в механике разрушения является
пластина с нарушением сплошности, представляющим собой разрез (трещину) и
являющимся концентратором напряжений. Рассмотрение трещин в хрупких телах
можно рассматривать как предельный случай концентрации напряжений.
Исторически первым является решение задачи о концентрации напряжений возле
кругового отверстия (Г.Кирш, 1898 г.). В современной интерпретации с
использованием функций напряжений Эри задача выглядит следующим образом.
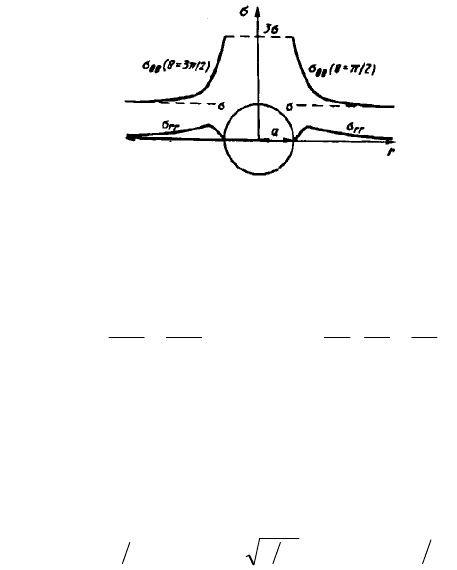
Рассматривается бесконечная пластина с круглым отверстием радиусом а,
находящаяся под воздействием одноосного напряжения . Для плоского
напряженного состояния в полярных координатах зависимости компонентов
напряжений при =/2 или =3/2 имеют вид (рис. 38)
Рис. 38. Распределение напряжений у круглого отверстия
в бесконечной пластине
.
2
3
,
2
3
2
1
4
4
2
2
4
4
2
2
r
a
r
a
r
a
r
a
rr
Дальнейшим развитием является анализ напряжений вокруг овального
отверстия в пластине в случае растяжения, чистого изгиба, чистого сдвига
(Г.В.Колосов, 1910 г., К.Инглис, 1913 г.), в соответствии с которым в вершине
отверстия возникает напряжение (рис. 39)
ababa
2
00
,2121
,
47
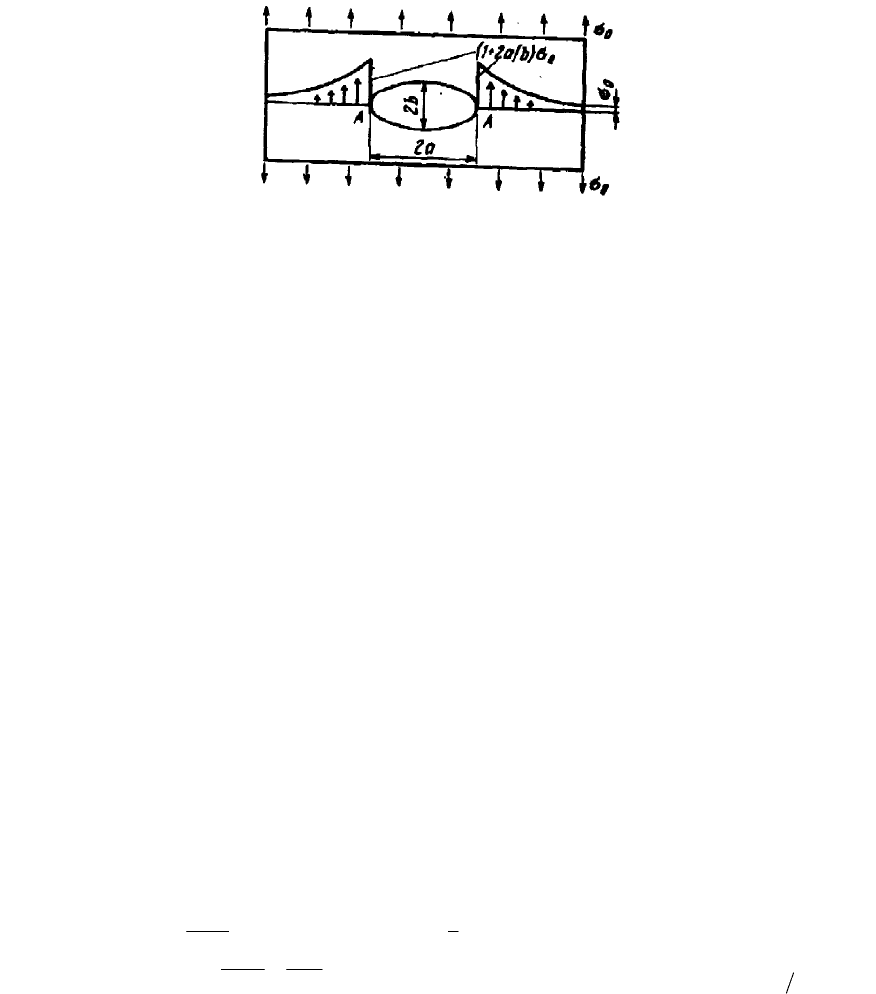
где
- радиус кривизны в вершине отверстия.
Рис. 39. Графическая иллюстрация результатов Колосова и Инглиса
В дальнейшем был поставлен и решен целый класс сингулярных краевых задач
теории упругости, т.е. граничных задач с особыми точками. Такими точками
являются, например, бесконечно удаленная точка, точка разрыва граничных условий
точка приложения сосредоточенной силы и т.д. При этом в линейных задачах
решение (или его производные, начиная с некоторого порядка) стремится к
бесконечности при приближении к особой точке. Поскольку граничная задача в
особой точке не определена, встает вопрос о формулировке физически
осмысленного дополнительного условия в такой точке, т.е. о постановке корректной
сингулярной краевой задачи.
Наиболее успешно для решения сингулярных задач используются мощные
методы, развитые Г.В.Колосовым и Н.И.Мусхелишвили для общего случая плоской
задачи теории упругости.
Допустим, что поле упругих смещений и деформаций не зависит от одной из
прямоугольных декартовых координат x, y, z, например, от z. В этом весьма общем
и важном случае все смещения и напряжения можно представить через функции
Ф(z), (z) и f(z), являющиеся аналитическими функциями комплексного
переменного z=x+iy в области, занятой телом. Первые две из них часто называют
потенциалом Колосова-Мусхелишвили. Выражения для комплексного
представления смещений и напряжений имеют следующий вид
,,,22,2 zzzzФzzФzizФzФ
xyyxyx
,14343,Re,2
илиzfzzzziu
где
- модуль сдвига;
- коэффициент Пуассона.
Для механики разрушения большой интерес представляет изучение
асимптотического распределения напряжений, деформаций и смещений вблизи
фронта трещины. Рассмотрим малую окрестность произвольно фиксированной
точки на гладком контуре трещины (рис. 40).
48

Рис. 40. Система координат и компоненты напряжений у кончика трещины
Общее корректное решение зависит от трех действительных параметров,
которые участвуют в решении на основе потенциалов Колосова-Мусхелишвили в
качестве множителей при различных членах асимптотики и которые определяются
из решения задачи. Каждый из указанных трех членов асимптотического
разложения соответствует одному из трех основных типов трещин (рис. 41).
Рис. 41. Основные виды смещений поверхности трещины
Окончательное решение дает распределение напряжений и смещений вблизи
края произвольной хрупкой трещины для указанных основных типов разрывов:
– нормальный разрыв
,
2
3
cos
2
cos
2
sin
2
,
2
3
sin
2
sin1
2
cos
2
,
2
3
sin
2
sin1
2
cos
2
r
K
r
K
r
K
I
xy
I
y
I
x
2
sin21
2
cos
2
,0,
2
r
K
u
I
yzxzyxz
,
;0,
2
cos22
2
sin
2
2
r
K
v
I
– поперечный сдвиг
,
2
3
sin
2
3
sin1
2
cos
2
,
2
3
cos
2
cos
2
sin
2
,
2
3
cos
2
cos2
2
sin
2
r
K
r
K
r
K
II
xy
II
y
II
x
,
2
cos22
2
sin
2
,0,
2
r
K
u
II
yzxzyxz
49

;0,
2
sin21
2
cos
2
2
r
K
v
II
– продольный сдвиг
.
2
sin
2
,0,0,
2
cos
2
,
2
sin
2
r
K
vu
r
K
r
K
III
xyzyx
III
yz
III
xz
Эти формулы были получены для случая плоской деформации; в случае
плоского напряженного состояния нужно взять в них
z
=0 и заменить на /(1+).
Формулы справедливы в малой окрестности края трещины, т.е. r должно быть
малым по сравнению с характерным линейным размером тела, например, длиной
трещины или расстоянием ее конца от свободной границы.
Трем типам разрывов в теории дислокаций соответствуют клиновые, краевые и
винтовые дислокации. Для трещин произвольного типа все величины K
I
, K
II
, K
III
отличны от нуля. Эти величины называются коэффициентами интенсивности
напряжений и имеют размерность силы, деленной на длину в степени три вторых.
10. Работа Гриффитса “Явление разрушения и течения
твердого тела”
Существует широкий круг явлений хрупкого разрушения, для которых
представление о критериях разрушения (теориях прочности) неприменимо.
Открытый А.Ф.Иоффе эффект увеличения прочности кристалла каменной соли при
растворении его поверхностных слоев, многочисленные случаи разрушения
металлических конструкций при напряжениях, меньших условного предела
текучести, а также многие другие явления разрушения, принципиально
необъяснимые с точки зрения теорий прочности, заставили ряд исследователей
отказаться от галилеева представления о прочности, как о некоторой константе
материала. Это направление в механике разрушения основано на изучении самого
процесса разрушения. Оно берет начало от работы Гриффитса, опубликованной в
1920 г. Гриффитс доказал, что концентрация напряжений в дефекте, установленная
Колосовым-Инглисом, позволяет превращать энергию деформирования в энергию
разрушения и что разрушение возможно только при постоянном подводе энергии. В
этой работе была рассмотрена следующая задача.
Пусть тонкая хрупкая пластина равномерно растягивается в одном направлении
напряжениями в своей плоскости. В пластине имеется сквозная трещина длины
2а, ориентированная перпендикулярно направлению растяжения. Длина трещины
считается малой по сравнению с размерами пластины. Опыт показывает, что,
начиная с некоторого , происходит развитие трещины, сопровождающееся
увеличением свободной поверхности. Поэтому Гриффитс ввел поверхностную
энергию хрупкого тела и сформулировал принцип, согласно которому
существующая трещина станет лавинообразно распространяться, если только
скорость освобождения энергии упругой деформации превзойдет прирост
поверхностной энергии трещины, т.е. если
G=
.4/
aU
50
