Лекции по Экономической кибернетике

Подождите немного. Документ загружается.

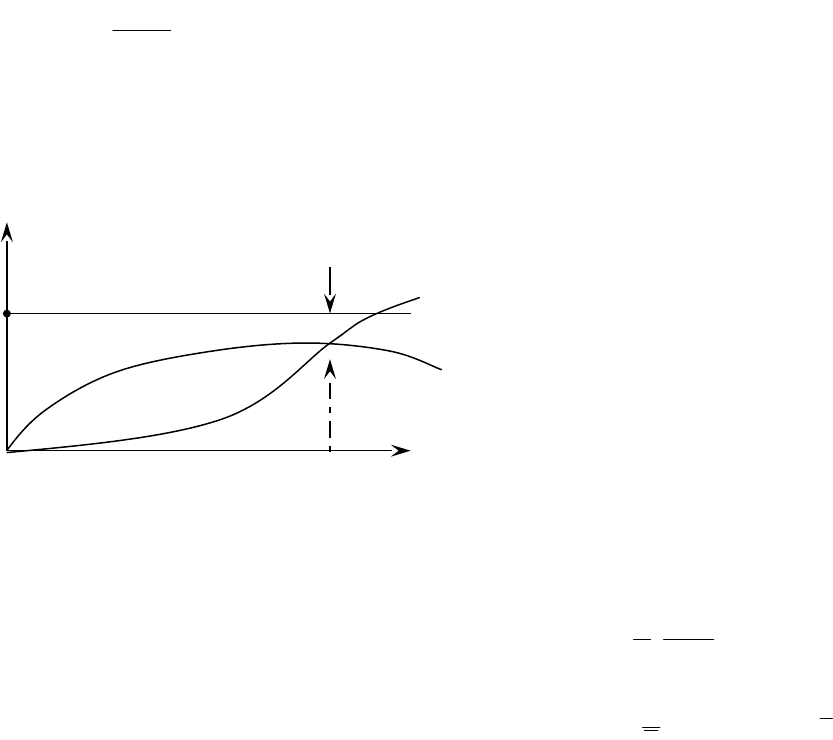
Предположим, что потенциальный выход представляет собой

ступенчатую функцию, где выполняются следующие условия:

(t) = 0; t≤0,

(t) = Y

; t≥0 (5.6),

порождаемую скачкообразным изменением интенсивности входной

переменной X(t). Тогда уравнение (5.4) записывается в следующей форме:

)(

YtY

tdY





а его решение при начальном условии Y(0)=0 имеет следующий вид:

1 Y- e (Y(t)







Рисунок 5.2.

Время Т, по истечению которого разность Y(t) - Y

(t) не превосходит

некоторые величины ε, определяется соотношением



ln1 Y

T 

и должно

соответствовать регламентированному или наблюдаемому лагу. Из этого

соотношения определяем величину λ. Если принять, что





, то при

Tt 

отклонение

ε =Y

/ε ≈ 0,379Y

. Площадь, заключенная между прямой линией Y

(t) и кривой

α (Рис.5.2) определяет состояние инерционного звена.

Показательное запаздывание достаточно хорошо описывает переходные

режимы, присущие многим реальным экономическим процессам. Таковы,

например, изменение потребительского спроса на товар, вызванный снижением

его цены, процесс освоения капитальных вложений на строительство объекта и

так далее. Однако для моделирования запаздывания, например, в спросе на

новый товар, порождаемого психологической инерцией потребителей, эта

форма не проходит. Здесь более приемлема кривая δ. Она может быть получена

с помощью модели, образованной двумя последовательно соединенными

Y(t)

(t)

-δ

инерционными звеньями типа зависимости (5.4). Это запаздывание второго

порядка описывается системой из двух дифференциальных уравнений, решение

которых дает кривую δ.

Для некоторых переходных режимов подходящая аппроксимация

запаздывания достигается с помощью показательных моделей третьего и более

высоких порядков. С ростом порядка увеличивается начальная фаза кривой

запаздывания и крутизна ее восходящей ветви, что дает более удовлетворенное

приближение к реальным процессам, имеющим такой характер.

Дискретные модели запаздывания

Пусть θ и τ - номера временных интервалов, а контролируемые моменты

времени отнесены к их концам. Дискретная модель запаздывания описывается

соотношением (2), в котором время t и лаг

целочислены:









(5.7)

В частном, но в распределенном случае

принимают равной единице

(годовой производственный цикл) и







Вместе с тем зависимость (5.7) сама является частным случаем

распределенного запаздывания, при котором предполагается, что

запаздывающий выход зависит от совокупности прошлых значений

потенциальной переменной, взятых с убывающими весами β

. Тогда

 















YYYY

1 ; причем

5.8 ...











Принимая в зависимости (5.8) веса убывающими по геометрической

прогрессии со знаменателем rU(1>r>0), получим модель, являющуюся

дискретным аналогом показательного запаздывания первого порядка:

 

1)1( этом при

)1(...)1(

































Yrr

YrrYrYrY

(5.9)

Соответствующее этой форме конечно-разностное уравнение имеет вид:

 





YYY 

, (10)

где λ=1-r, а Y

τ+1

= Y

+ ΔY

τ = 1, 2, ....

Тема 9. Общественное потребление

Нормативные методы определения потребности населения

При формировании рациональных норм потребления исходят из

предположения, что на каждом данном этапе состояния экономики объективно

существует некоторый разумный, ограниченный сверху уровень потребностей

человека в том или ином благе, к достижению которого он стремиться в меру

своих возможностей.

Статистический анализ потребления имеет целью количественно оценить

влияние на него тех или иных факторов и проследить закономерности его

изменения. Такая информация необходима для обоснования различных

мероприятий по повышению уровня жизни и вместе с тем используются при

планировании народного потребления.

Исходным этапом является построение моделей, описывающих

зависимость интенсивности потребления семей от совокупности факторов,

наиболее существенных и поддающихся количественному измерению.

Наблюдения показывают, что ими являются доходы и половозрастная

структура семьи.

Допустим, что известны нормативы С

потребления i-х групп товаров и

услуг для каждого j-го члена семьи в соответствии с его полом, возрастом и

категорией труда. Примем в качестве условной потребительской единицы

взрослого мужчину, занятого механизированным трудом, для которого норма

потребления равна С

. Тогда отношения





(6.1)

определяют в этом масштабе (потребительской шкале) число потребительских

единиц каждого из членов семьи по i–му благу, а





– общее

число таких

единиц для семьи.

Далее согласно нормативному бюджету расходы для j-го члена на

потребление распределяются между отдельными компонентами с удельными

весами α

(где

Σα

=1). Тогда путем взвешивания отдельных потребительских

шкал по их долям в нормативном бюджете можно построить итоговую шкалу j-

го члена семьи по расходам на все товары и услуги. Эта шкала определяет

итоговое число γ

= Σγ

потребительских единиц указанного члена семьи

с присущими ему признаками, а для семьи в целом

j i

iju







(6.2)

Шкалы γ

и доли α

не зависят от доходов семьи. Тогда при построении

функции потребления семьи с одинаковым числом потребительских шкал

могут быть объединены в одну группу. Таким образом, нормативные

потребительские шкалы удобны для анализа и планирования потребления. При

расчете шкал используются статистические данные о фактическом

потреблении.

Формирование потребления

Формирование моделей потребления на основе статистических данных

проводят в три этапа:

1. Выбор показателей дохода и структуры семьи;

2. Выбор уравнения регрессии интенсивности потребления данного блага

на эти показатели;

3. Оценка параметров регрессии по выборочным данным.

В качестве показателей дохода может приниматься его совокупная

величина, доход на душу или потребительскую единицу. Структуру семьи

можно оценить в единицах потребительских шкал, в долях числа детей и

взрослых или по конкретному составу типовых семей.

С увеличением интенсивности денежных доходов (D) интенсивность

расходов на потребление (Р) также увеличивается. Одновременно изменяется

структура потребления, причем характер ее изменения зависит главным

образом от структуры семьи.

При изучении закономерностей потребления и логическом обосновании

вида соответствующих функций важную роль играют коэффициенты

эластичности потребления по факторам, характеризующие реакцию

потребителя на изменение соответствующего фактора.

Предположим, зависимость интенсивности потребления i-го блага от

совокупного дохода D для семей γ=γ

выражена функцией.

= f

(D,γ

) (6.3),

непрерывной вместе с двумя первыми производными. Выберем произвольную

точку A с координатамиU(D

iА

). Пусть ∂D малое приращение интенсивности

дохода в окрестности этой точки, а







- соответствующее относительное

приращение этого фактора. Вызванное им относительное изменение

интенсивности расхода имеет следующий вид:







Тогда

E 







(6.4),

есть коэффициент эластичности потребления i-го блага по доходу в выбранной

точки. При фиксировании γ он является в общем случае функцией дохода.

Коэффициент эластичности безразмерен и интерпретируется так: если он равен,

например двум, то при неизменном γ увеличение дохода на 1% вызывает рост

расходов на потребление на 2%. Аналогично для семей, однородных по

величине дохода, величина









(6.5),

исчисленная в точке с координатами (γ

, Р

iА

), представляет собой некоторый

вид эластичности: при изменении на 1% числа единиц семьи с доходом D=D

и γ=γ

расходы на потребление i-го блага изменяются на Еγi %.

Коэффициент эластичности можно рассчитать непосредственно по

статистическим данным. Пусть для двух групп семей, взятых из выборки,

однородной относительно γ, их доходы и потребительские расходы составляют:

=30 P

=18

=32 P

=21.

Рассчитаем эластичность Е

в точке D

, P

. Поскольку вариации

переменных сравнительно малы, можно принять, что связь между показателями

линейна. Тогда:

5,2

3032

1821











Следовательно, рост дохода в точке (30, 18) на 1% вызывает увеличение

расхода на потребление на 2.5%.

При формировании комплекса функций потребления, охватывающего все

его компоненты, очевидно, должно быть обеспечено его условие





(6.6)

(n – число групп потребительских благ)

то есть сумма расходов на отдельные группы благ должна быть равна чистому

совокупному доходу. Если для всех функций принять линейную связь между

расходами на потребление и доходом

DCCP

iii





(i=1,…,n) (6.7),

то Ĉ

и Ĉ

параметры регрессии, оцененные по выборочным данным, должны

удовлетворять ограничениям

1 и 0





СС



(6.8)

Выбор линейной связи при соблюдении условий (6.8) равносилен

принятию гипотезы о независимости структуры потребления от доходов.

Построение таким образом функций потребления могут служить для расчета

потребительских шкал по данным бюджетной статистики. Однако они не

всегда обеспечивают требуемую точность аппроксимации выборочных данных.

Более удовлетворительные результаты достигаются с помощью функции вида:

iii

DCP



(6.9)

линейных относительно логарифмов lgP

= lgC

+ C

1i*

lgD

Функции спроса

Для планирования народного потребления необходимо располагать

надежной информацией, характеризующей потребности населения и их

динамику. Наиболее отчетливо они проявляются в потребительском спросе,

структура которого заметно отличается от фактического потребления, так как

предложение тех или иных товаров и услуг часто не соответствует потребности

в них. Эта неудовлетворенная потребность не проявляется в семейных

бюджетах и не находит отражения в функциях потребления. Между тем такая

информация имеет важнейшее значение для планирования производства. Она

может быть получена только путем систематического изучения спроса и в

сочетании с бюджетными данными, позволяет выявить его закономерности,

прогнозировать его изменение и на этой основе обеспечивать согласование

планов производства с потребностями населения.

При анализе спроса и практических расчетах приходится прибегать к его

упрощенному моделированию. Наиболее простые строятся в виде

статистического преобразователя

)P(D f C

ii i

,

(6.10),

где

– интенсивность спроса.

Такая взаимосвязь реалистична только при отдельных условиях:

1) колебание цены и спроса должны быть столь заметными, чтобы их

соотношения можно было измерить;

2) заменяемость данного блага и колебание дохода наоборот

незначительны;

3) влияние запасов товаров должно быть пренебрежительно мало;

4) несущественными должны быть возмущения, порождаемые

неучтенными факторами.

Для большинства товаров интенсивность спроса уменьшается с

увеличением их цены (при неизменном доходе). Но здесь возникают и

аномалии - с повышением общего индекса цен спрос на дешевые товары

увеличивается. Из этого следует, что эластичности спроса по доходу

E 





(6.11)

для большинства благ положительны, а эластичности по их ценам

отрицательны

E 





(6.12)

В более сложных моделях при анализе спроса на данное благо учитывает

также цены на некоторые другие товары, которые могут оказать на него

заметное влияние. В функцию обычно включают ограниченное число таких

переменных. Примером может служить линейная модель спроса на говядину

построенная в США.

сГДГ

PPIС 0637.00839.00287.04892.2 

где I

– индекс доходов;

Рг – цена говядины;

Рс – цена свинины.

Временным рядом спроса и факторов, по которым строятся описанные

функции, присущи весьма заметные автокорреляции, обусловленные тем, что

производящие их случайные процессы, как правило, нестационарны.

Чаще всего автокорреляции исключаются путем включения в число

переменных времени как дополнительного фактора.

При этом функция спроса принимает следующий вид:

     

 

ttPtDtC





(6.13)

В ней фактор t отражает совокупное влияние всех неучтенных

воздействий, порождающих тенденцию в спросе.

В тех случаях, когда можно предполагать, что существенной является

только стохастическая связь между соседними членами временного ряда,

автокорреляцию устраняют путем включения в модель запаздывающей

переменной

 

 

1τ τττ





iii

CPDС



(6.14)

Тема 10. Линейные модели оптимизации в управлении экономикой

Общая постановка задачи линейного программирования (ЗЛП)

Линейное программирование – это область математики,

разрабатывающая теорию и численные методы решения задач нахождения

экстремума (max или min) линейной функции многих переменных при наличии

линейных ограничений, то есть линейных равенств или неравенств,

связывающих эти переменные.

С помощью задач линейного программирования решается широкий круг

вопросов планирования экономических процессов, где ставится цель поиска

наилучшего (оптимального) решения.

Найти вектор

=(Х

, Х

, ..., Х

)

максимизирующий линейную форму

 

max







xCxf

j=1, ..., n (7.1)

и удовлетворяющий условиям:

bxa 



1

(7.2)

0

(7.3)

Линейная функция

)xf(

называется целевой функцией задачи, условия

(7.2) - функциональными, а условия (7.3) – прямыми ограничениями

задачи.

Вектор

=(Х

, Х

, ..., Х

), компоненты которого удовлетворяют

функциональным и прямым ограничениям задачи, будем называть планом, или

допустимым решением ЗЛП.

Все допустимые решения образуют область определения ЗЛП, или

область допустимых решений. Допустимое решение, максимизирующее

целевую функцию

)xf(

называется оптимальным планом задачи:

)xf()xf( max



где

) x..., , x,(x X



– оптимальное решение ЗЛП.

Будем считать, что ЗЛП записано в канонической форме, если ее целевая

функция максимизируется, ограничения имеют вид равенств с правой

неотрицательной частью и все переменные неотрицательны.

Задачи оптимизации производственной

программы предприятия

В качестве критериев оптимальности будем использовать: прибыль,

себестоимость, затраты станочного времени, номенклатуру произведенной

продукции.

Неизвестным в задаче являются объемы выпуска продукции каждого

вида. Введем следующие обозначения:

j, s

– объем производства j-го продукта по s-му технологическому

способу (j = 1,…, n); (s = 1,…, Qj);

n – количество видов выпускаемой продукции;

– число технологических способов, используемых при

производстве j-го продукта;

– наличие i-го ресурса (i = 1,…, m);

m – количество типов используемых ресурсов;

i, j, s

– норма затрат i-го ресурса на производство единицы j-го продукта

по

s-му технологическому способу;

j, s

– прибыль от производства j-го продукта по s-му технологическому

способу;

– задание (госзаказ) по выпуску j-ого вида продукции;

i, j

– себестоимость производства j-го продукта по s-му

технологическому способу;

Pi,j -- заданный уровень прибыли.

Задача на максимум прибыли

Используя принятые выше обозначения, модель задачи можно записать в

следующем виде.

jis

ijsijs

QSX

bXa

njXpxf

...,1,0

,...,1max,)(











Выражение

)xf(

максимизирует совокупную прибыль всего объема

выпускаемой продукции всех видов. В данной модели оптимизация возможна

за счет включения в план выпуска наиболее выгодных видов продукции и за

счет выбора для каждого вида продукции наиболее выгодных способов ее

производства. Способы производства отличаются, друг от друга величиной

удельной прибыли и нормами затрат ресурсов. Ограничения означают, что для

любого из ресурсов его суммарный расход на производство всех видов

продукции по всем способам не превосходит имеющихся ресурсов.

При составлении плана производства приходится учитывать не только

ограниченность ресурсов, но и директивные задания (госзаказы) по выпуску

продукции. При этом модель дополняется ограничением вида X

, а свобода

выбора значительно снижается.

Задача на минимум себестоимости производства

Экономико-математическая модель задачи имеет вид:

;,...,1;

min)(













jjsjs

ijsijs

jsjs

QPXp

mibXa

XCxf

При построении модели на минимум затрат наличие ограничений типа

«больше» или «равно» обязательно. Отсутствие ограничений снизу ведет к

оптимальному плану с нулевыми значениями переменных, которые дадут

наименьшее значение критерия оптимальности. Такое решение абсурдно с

экономической точки зрения.

Все допустимые решения задачи, которой соответствует данная модель,

различаются по видам затрат, но одинаковы с точки зрения результата.

Результатом выступает заданная производственная программа. Выбор

наилучшего плана производства по минимуму затрат возможен вследствие

эквивалентности результатов по всем вариантам.

Следует подчеркнуть, что при различной величине результатов вариант с

меньшими затратами может быть и не лучшим: просто с наименьшими

затратами мы достигаем и меньшего результата.

Задача на максимум выпуска продукции в заданном

ассортиментном соотношении (на максимум комплексов)

Введем новые обозначения:

– количество изделий вида j, которые входят в некоторый комплект

(например, комплект запасных частей для автомобиля).

Функция максимума комплектной продукции будет следующая:

,...,1},{minmax 

то есть общее количество комплектов К определяется количеством изделий, из

которых можно сформировать меньше всего «порций», объемом K

. Эти

изделия определяют, как бы «узкое место» в формировании комплектов, к

максимальной «расшивке» которого следует стремиться.

Введем новое обозначение



, которое связывает количество

комплектов К с условием по формированию комплектов. Модель в общем виде

с учетом наличия нескольких способов производства имеет следующий вид: