Лекции по численным методам (34 часа)

Подождите немного. Документ загружается.

ОБ ИСТОРИИ ВОЗНИКНОВЕНИЯ ПРЕДМЕТА

«ЧИСЛЕННЫЕ МЕТОДЫ».

В связи с развитием новой вычислительной техники инженерная

практика наших дней все чаще и чаще встречается с математическими

задачами, точное решение которых получить весьма сложно или невозможно. В

этих случаях обычно прибегают к тем или иным приближенным вычислениям.

Вот почему приближенные и численные методы математического анализа

получили за последние годы широкое развитие и приобрели исключительно

важное значение.

Новые вычислительные средства вызвали переоценку известных методов

решения задач с точки зрения целесообразности их реализации на ЭВМ и

стимулировали создание более эффективных. В то же время приспособление

какого-либо метода для работы на ЭВМ выдвинуло специфическую проблему

«устойчивости вычислительной схемы».

Вычислительная математика = ЭВМ + Численные методы

Предметом изучения вычислительной математики являются численные

методы решения задач математического анализа: изучение алгоритма метода,

условия сходимости итерационных методов, изучение границ применимости

методов, исследования оценок погрешностей методов и вычислений. Главным

разделом вычислительной математики является реализация численных методов

на ЭВМ, то есть составление программы для требуемого алгоритма и решения

конкретной задачи с помощью составленной программы.

Любая прикладная задача формируется исходя из определенного

физического смысла некоторого процесса (распределение тепла в стержне,

описание траектории движения объектов). Прикладная математическая задача

может быть сформулирована, например, из описания некоторой экономической

модели (задача распределения ресурсов, задача планирования производства,

транспортная задача перевозки грузов, оптимальных в заданном смысле).

Следовательно, для постановки любой прикладной задачи нужна

математическая модель. Поэтому, можно выделить следующие этапы решения

задач на ЭВМ:

1) Описание математической модели задачи на основе физической или

экономической модели.

2) Изучение методов решения поставленной математической модели

задачи и создание новых методов.

3) Выбор метода решения задачи исходя из заданной точности решения и

особенностей задачи.

4) Составление блок-схемы программы для решения задачи на ЭВМ.

5) Отладка программы и оценка полученных результатов. Подстановка

решения в уравнение (например, при решении нелинейных уравнений и систем,

при решении систем линейных алгебраических уравнений). Решение одной и

той же задачи различными методами и решение задачи различными

пользователями. Проверка соответствия решения математической и физической

модели задачи. В случае несоответствия решений происходит возврат на более

ранние этапы решения задачи.

6) Решение задачи на ЭВМ, построение графиков, получение оценки

погрешностей, обоснование результатов.

1. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Нелинейными уравнениями называются уравнения вида

 

0xf

. (1)

Здесь

 

- нелинейная функция:

– нелинейная алгебраическая функция вида

... axaxaxa





;

– трансцендентные функции – тригонометрические, обратные

тригонометрические, логарифмические, показательные и гиперболические

функции;

– комбинирование этих функций

 

xx sin



Решением нелинейного уравнения (1) является такая точка

, которая

при подстановке в уравнение (1) обращает его в тождество. На практике не

всегда удается подобрать такое решение. В этом случае, решение уравнения (1)

находят с применением приближенных (численных) методов. Тогда решением

нелинейного уравнения (1) будет являться такая точка

, при подстановке

которой в уравнение (1) последнее будет выполняться с определенной

степенью точности, т.е.

)(

, где



- малая величина. Нахождение таких

решений и составляет основу численных методов и вычислительной

математики.

Решение нелинейных уравнений распадается на два этапа: отделение

корней уравнений и уточнение корней нелинейных уравнений.

На первом этапе необходимо исследовать уравнение и выяснить, имеются

корни или нет. Если корни имеются, то сколько их, и затем определить

интервалы, в каждом из которых находится единственный корень.

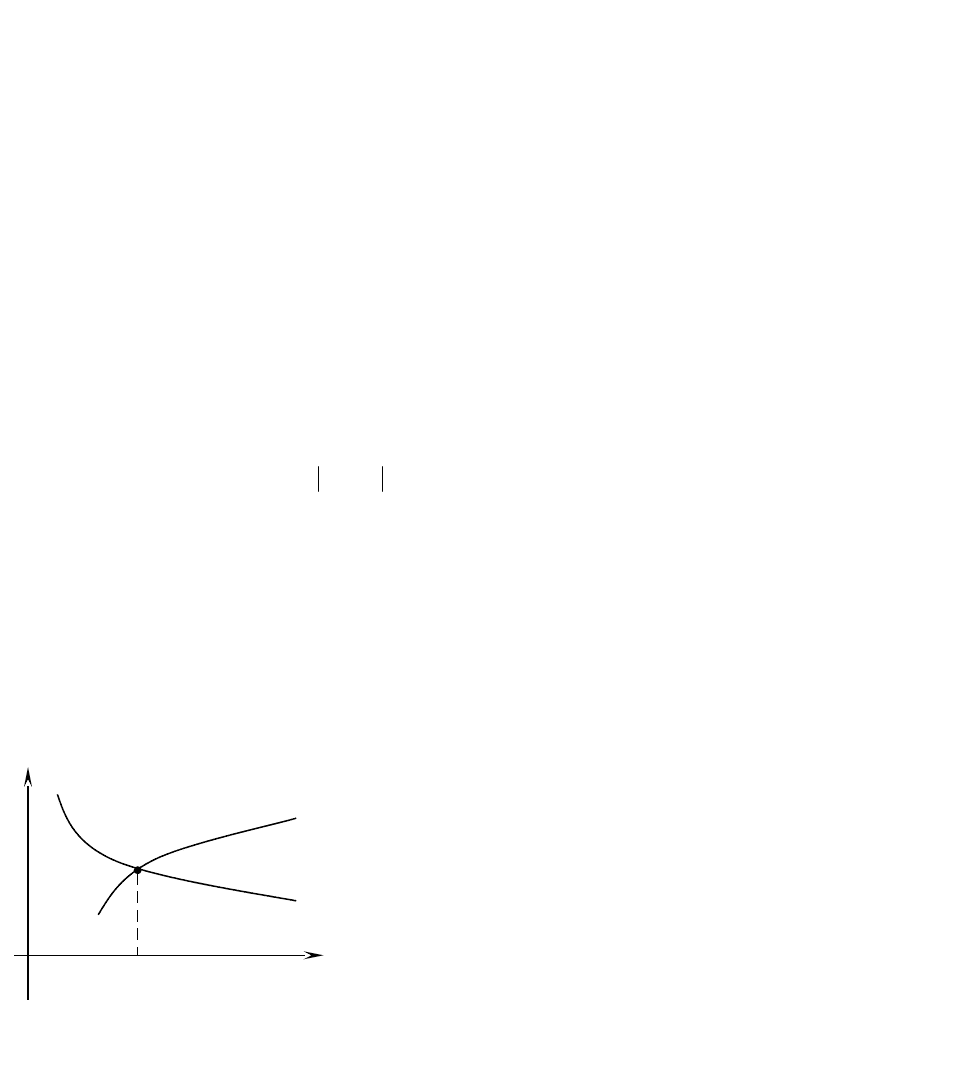
Первый способ отделения корней –

графический. Исходя из уравнения (1), можно

построить график функции

 

xfy 

. Тогда точка

пересечения графика с осью абсцисс является

приближенным значением корня. Если

 

имеет сложный вид, то представим ее в виде

разности двух функций

     

xxxf



. Так

как

 

0xf

, то выполняется равенство

   



. Построим два графика

 



 



 



Рис.1

 



. Значение



- приближенное значение корня (Рис.1), являющееся

абсциссой точки пересечения двух графиков.

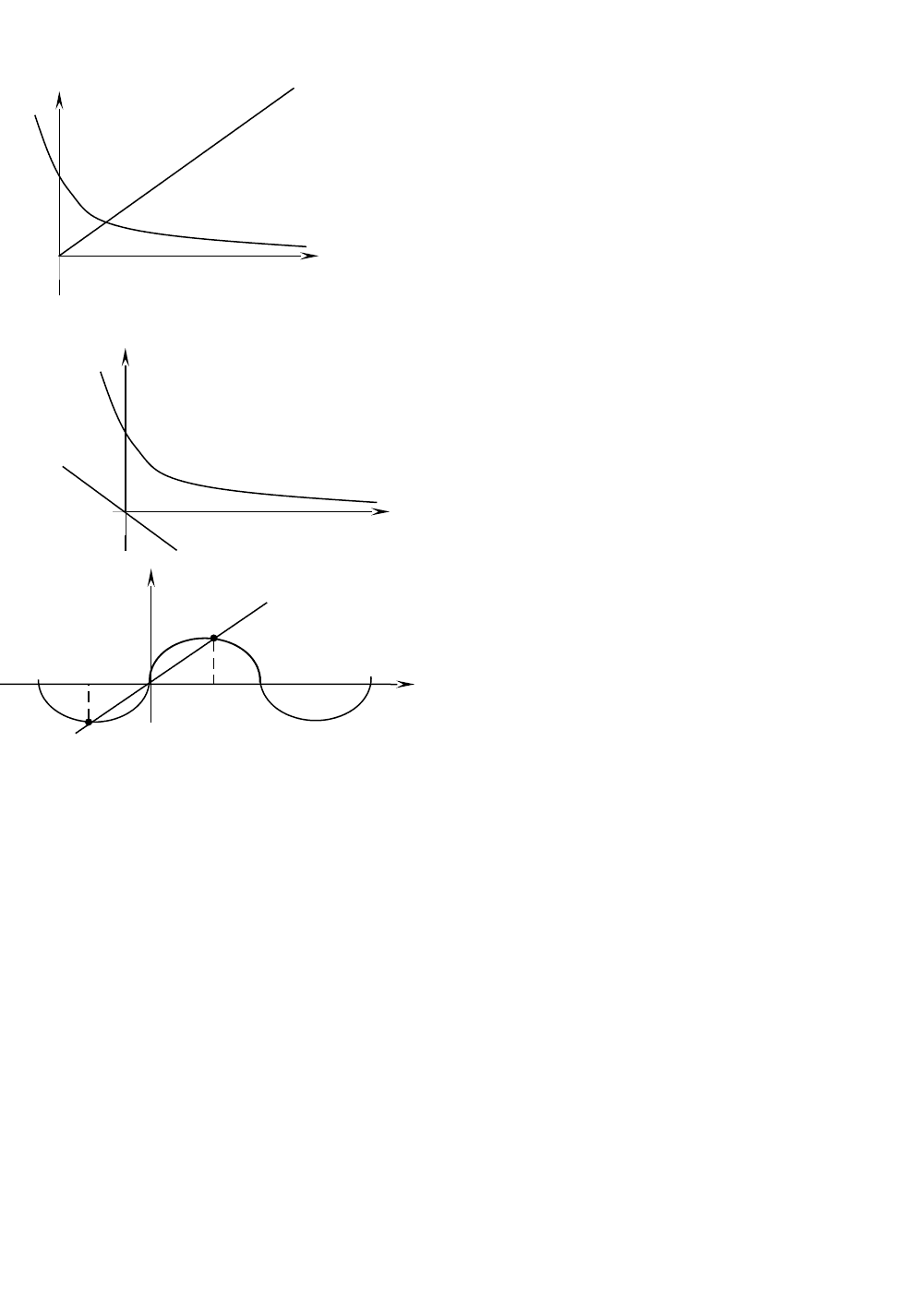
Пример 1. Пусть дано нелинейное

уравнение вида

0

 x

. Решим его

графическим методом. Для этого представим

уравнение в виде

   

 xx

, где

 

xx 

;

 





Графики функций

xy 

;





представлены

на Рис.2, из которого видно, что исходное

уравнение имеет единственный корень



Пример 2. Пусть задано

нелинейное уравнение вида

0



или





. Построив два графика

функций

xy 





, видим, что

исходное уравнение не имеет корней

(Рис.3).

Пример 3. Для нелинейного

уравнения вида

0  xsinx

с помощью

аналогичных преобразований и

построений получим, что исходное

уравнение имеет несколько (три) корней

(Рис.4).

Второй способ отделения корней

нелинейных уравнений –

аналитический. Процесс отделения корней нелинейных уравнений

основывается на следующих теоремах.

Теорема 1. Если функция

 

непрерывна на отрезке

 

ba,

и меняет на

концах отрезка знак (т.е.

   

0bfaf 

), то на

 

ba,

содержится хотя бы один

корень.

Теорема 2. Если функция

 

непрерывна на отрезке

 

ba,

, выполняется

условие вида

   

0bfaf

и производная

 



сохраняет знак на

 

ba,

, то на

отрезке имеется единственный корень.

Теорема 3. Если функция

 

является многочленом

степени и на

концах отрезка

 

ba,

меняет знак, то на

 

ba,

имеется нечетное количество

корней (если производная

 



сохраняет знак на

 

ba,

, то корень

единственный). Если на концах отрезка

 

ba,

функция не меняет знак, то

уравнение (1) либо не имеет корней на

 

ba,

, либо имеет четное количество

корней.

При аналитическом методе исследований необходимо выявить интервалы

монотонности функции

 

. Для этого необходимо вычислить критические





xy 

Рис.2





xy 

Рис.3

Рис.4

xy 

xy sin

точки

 

 ,...,,

, т.е. точки, в которых первая производная

 

f 



равна нулю

или не существует. Тогда вся числовая ось разбивается на интервалы

монотонности

),(

1ii 



. На каждом из них определяется знак производной

 



, где

),(x

1iii 



. Затем выделяем те интервалы монотонности, на которых

функция

 

меняет знак. На каждом из этих интервалов для поиска корня

используются методы уточнения корней.

Одним из методов уточнения корня на отрезке является метод

половинного деления (метод дихотомии).

1.1. Метод половинного деления.

Для уточнения корня нелинейного уравнения (1) на отрезке

 

ba,

, где

   

0bfaf

, а производная сохраняет знак, разделим отрезок

 

ba,

пополам и

исследуем знак функции в полученной точке

, где





. Из двух отрезков

 

ca,

 

bc,

выбираем тот, на котором функция меняет знак. Уменьшая новый

отрезок в два раза, повторяем процесс и т.д. Получим последовательность

отрезков

],...b,a[],...,b,a[],b,a[

nn2211

, на концах которых выполняется

неравенство

   

0

bfaf

, где

)ab(ab



. Последовательность

,...a,...,a,a

n21

является монотонной неубывающей ограниченной

последовательностью; а

,...b,...,b,b

n21

- монотонной невозрастающей

ограниченной последовательностью. Следовательно, существует предел:





)ab(lim)ab(lim

Тогда





blimalim

до тех пор, пока не будет получен корень с заданной точностью.

Кроме метода дихотомии для уточнения корня на

 

ba,

применяются

итерационные методы (методы последовательных приближений).

1.1. Метод простых итераций.

Пусть известно, что нелинейное уравнение

 

0xf

имеет на отрезке

 

ba,

единственный вещественный корень

],[ ba

. Требуется найти этот корень с

заданной точностью. Применяя тождественные преобразования, приведем

уравнение к виду

 

xx 

(2)

Выберем произвольно приближенное значение корня

 

bax ,



вычислим

 

xx 

. Найденное значение

подставим в правую часть

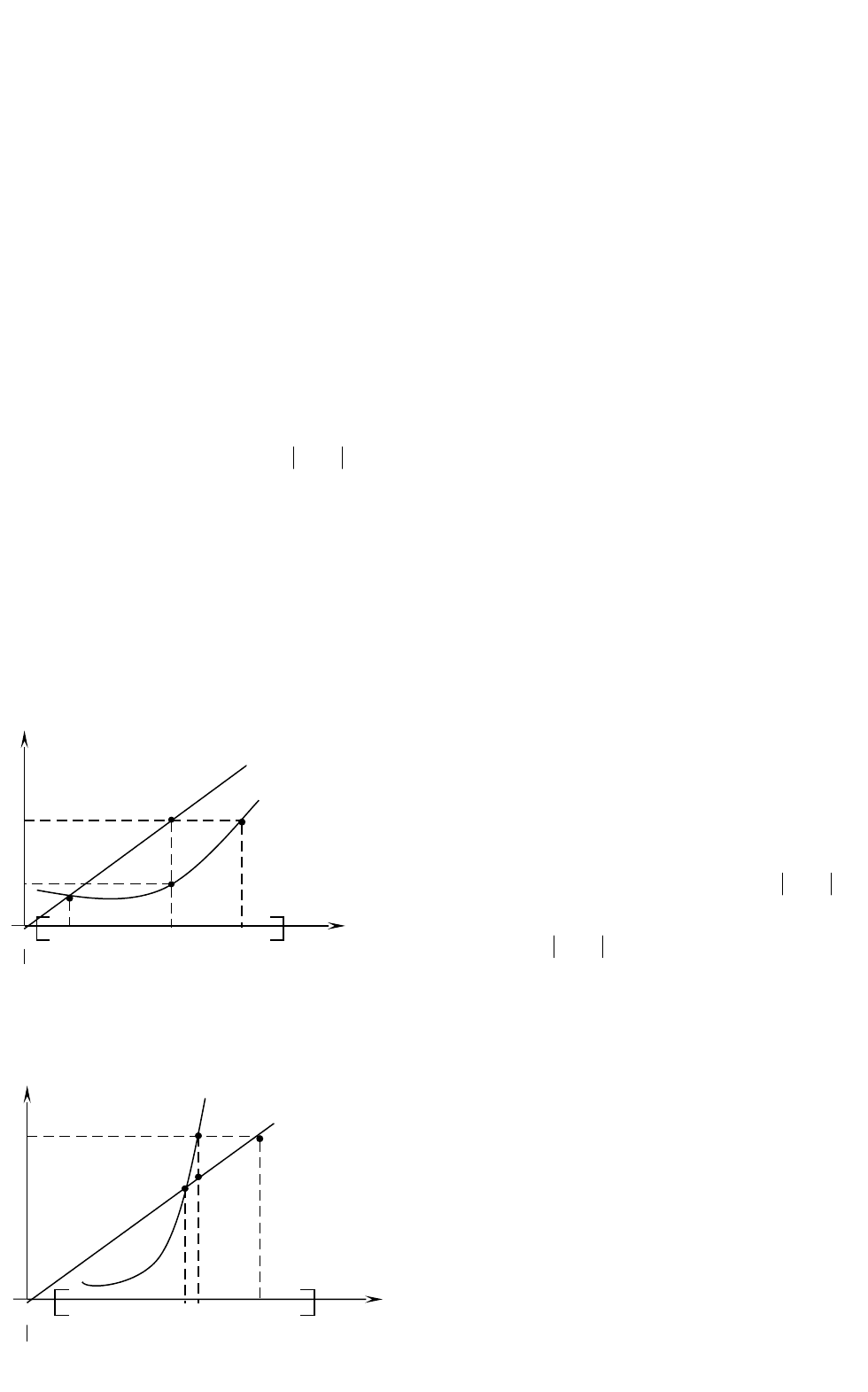
соотношения (2) и вычислим

 

xx 

. Продолжая процесс вычислений

дальше, получим числовую последовательность

,...,,

210

xxx

. Если существует

предел этой последовательности, то он и является корнем уравнения (2). В

самом деле, пусть





xlim

. Тогда, переходя к пределу в равенстве

 

limlim







и учитывая непрерывность функции

 

x

на отрезке

 

ba,

получим

limlim





















или

 



Корень можно вычислить с заданной точностью по итерационной

формуле

 

,...2,1,0,





nxx

(3)

Достаточное условие, при котором итерационный процесс сходится, определяет

следующая теорема: пусть функция

 

x

определена и дифференцируема на

отрезке

 

ba,

, причем все ее значения

 

],[ bax 

и выполняется условие

 

 

baxqx ,,1 



, (4)

тогда процесс итераций (3) сходится независимо от начального значения

 

bax ,



и предельное значение



 lim

является единственным корнем

уравнения (2) на

 

ba,

. Точка



называется неподвижной точкой для уравнения

(2).

1.2. Геометрическая интерпретация метода простых итераций.

Построим два графика:

xy 

 

xy 

. Абсцисса точки пересечения

графиков – корень



. Построим

итерационный процесс. Зададим

],[

bax 

Вычислим

 

xx 

– первое приближение и

 

xx 

– второе приближение. В первом

случае (Рис.5) процесс сходящийся (

 

1



). Во втором случае (Рис.6) процесс

расходящийся (

 

1



1.3. Приведение нелинейного уравнения

 

0xf

к виду

 

xx 

, допускающему сходящиеся итерации.

Выполнение условия сходимости

можно добиться путем перехода от

исходного уравнения

0)( xf

эквивалентному виду

 

xx 

следующим

образом: умножим обе части уравнения (1)

на

0constc

, затем прибавим к обеим

частям по

, тогда

 

xxcfx 

. Обозначим

 

xy 



Рис.5

 

xy 



Рис.6

   

xcfxx 

, тогда

 

xx 

. Константа

выбирается так, чтобы выполнялось

достаточное условие сходимости итерационного процесса (4), т.е.

   

 

baxxfcx ,,11 







. Это условие равносильно

 

111 



 xfc

, отсюда

 







при

 

 

baxxf ,,0 



 







при

 

 

baxxf ,,0 



Требуемую точность вычислений можно обеспечить путем

использования оценок приближения

к корню







; 2)





nnn

При

q

второе неравенство примет

вид

1



nnn

xxx

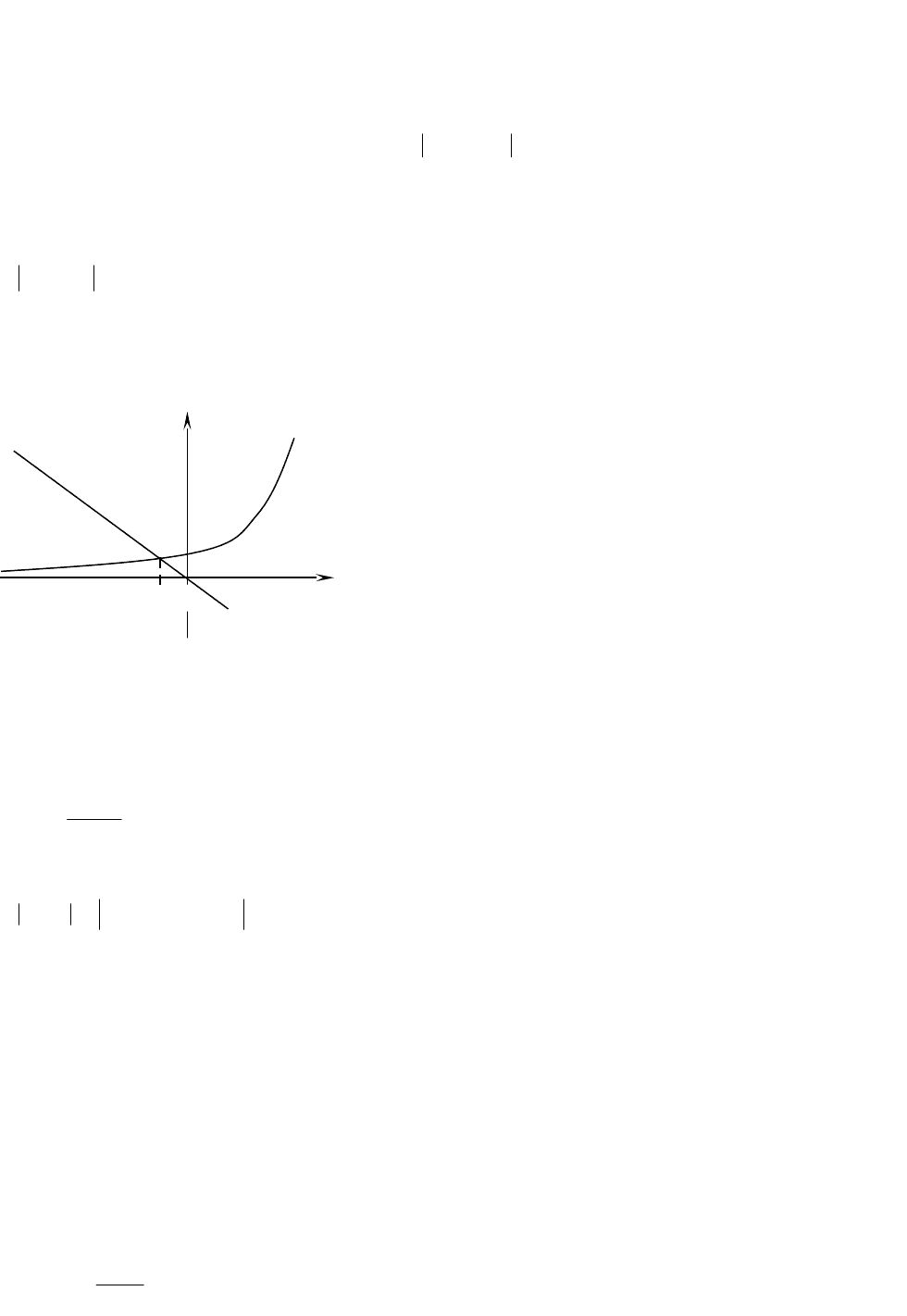
. Таким образом, если



1nn

, то



. Очевидно, что

чем меньше

, тем быстрее сходится

процесс итераций. Практически грубую

оценку приближенного решения можно

получить без дополнительных вычислений

при

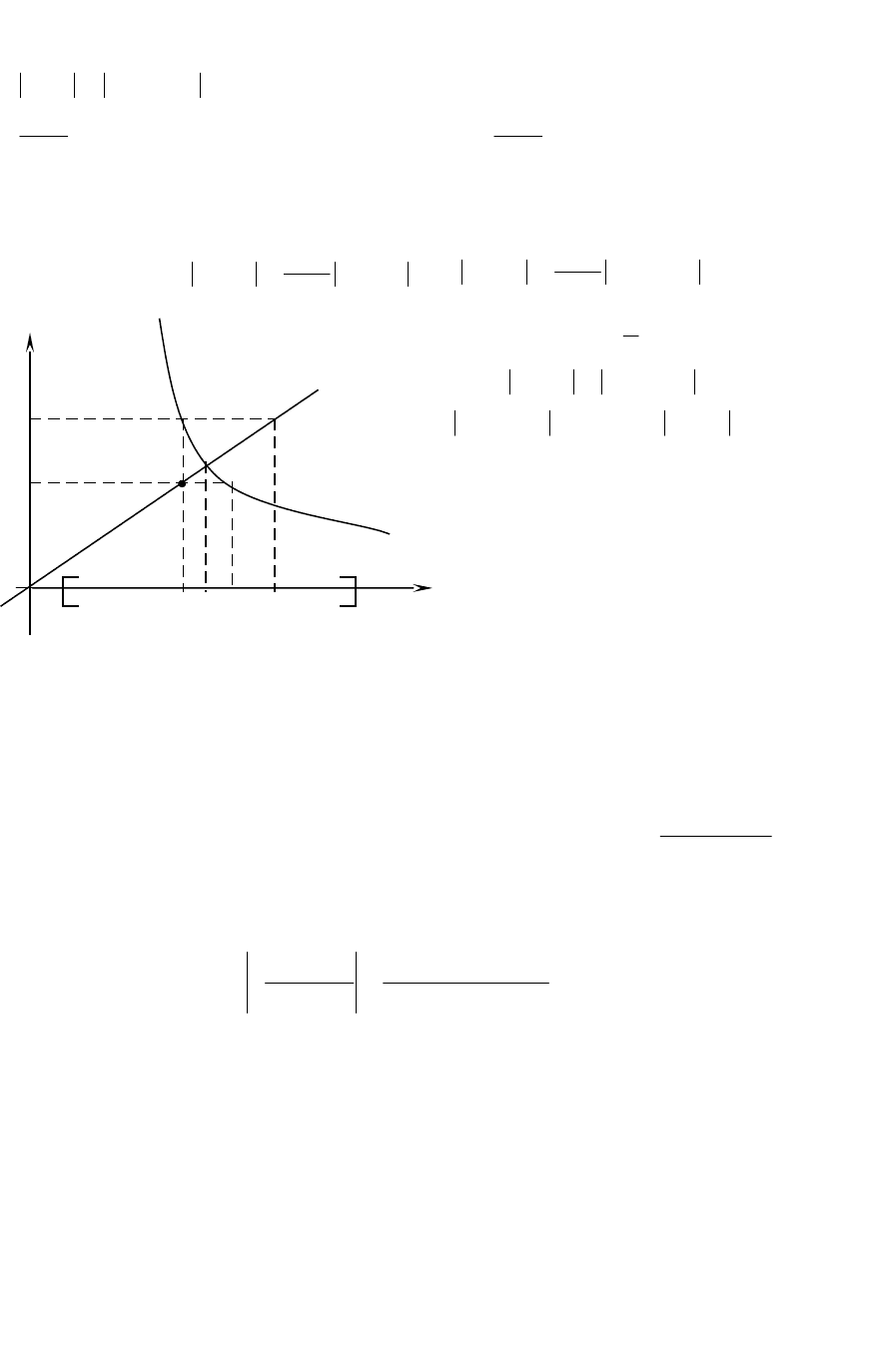
0)(

 x

. В этом случае (Рис.7)

итерации попеременно оказываются то с

одной, то с другой стороны корня, так что

корень заключен в интервале

),(

1nn

. Это надежная, хотя и грубая оценка, но

она неприменима при

0)(

 x

, когда итерации сходятся к корню монотонно,

т.е. с одной стороны. Вблизи корня итерации сходятся примерно так же, как

геометрическая прогрессия со знаменателем







. Чтобы сумма

дальнейших членов прогрессии не превосходила



, должен выполняться

критерий сходимости













)(

nnn

nnnn

xxx

При выполнении этого условия процесс итераций можно прекращать. Метод

простых итераций и почти все другие итерационные методы имеют два

достоинства:

- являются универсальными и самоисправляющимися, то есть любая

неточность на каком – либо шаге итераций не отразится на конечном

результате, а лишь на количестве итераций. Подобные ошибки устойчивы даже

по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не

выбрасывает очередное приближение за пределы области сходимости.

- позволяют достигнуть любой заданной точности при любом начальном

приближении

 

bax ,



Недостатки методов:

- трудность приведения уравнения (1) к виду (2).

 

xy 



Рис.7

- если начальное приближение

далеко от корня, то число итераций

достаточно большое. Объем вычислений возрастает.

Процесс итераций заканчивается при выполнении двух критериев:

1) Когда два последних приближения отличается между собой по

модулю на заданную величину





 nn

. Этого критерия недостаточно,

так как в случае крутизны графика, данное условие будет выполнено, но

1n

может находиться далеко от корня.

2) Мера удовлетворения уравнению последнего приближения корня:

 



1n

. Отдельно второго критерия недостаточно, так как при пологой

функции

)(xf

условие может быть выполнено, но

1n

может быть далеко от

корня.

Пример. Методом итераций найти корни уравнения

0 xe

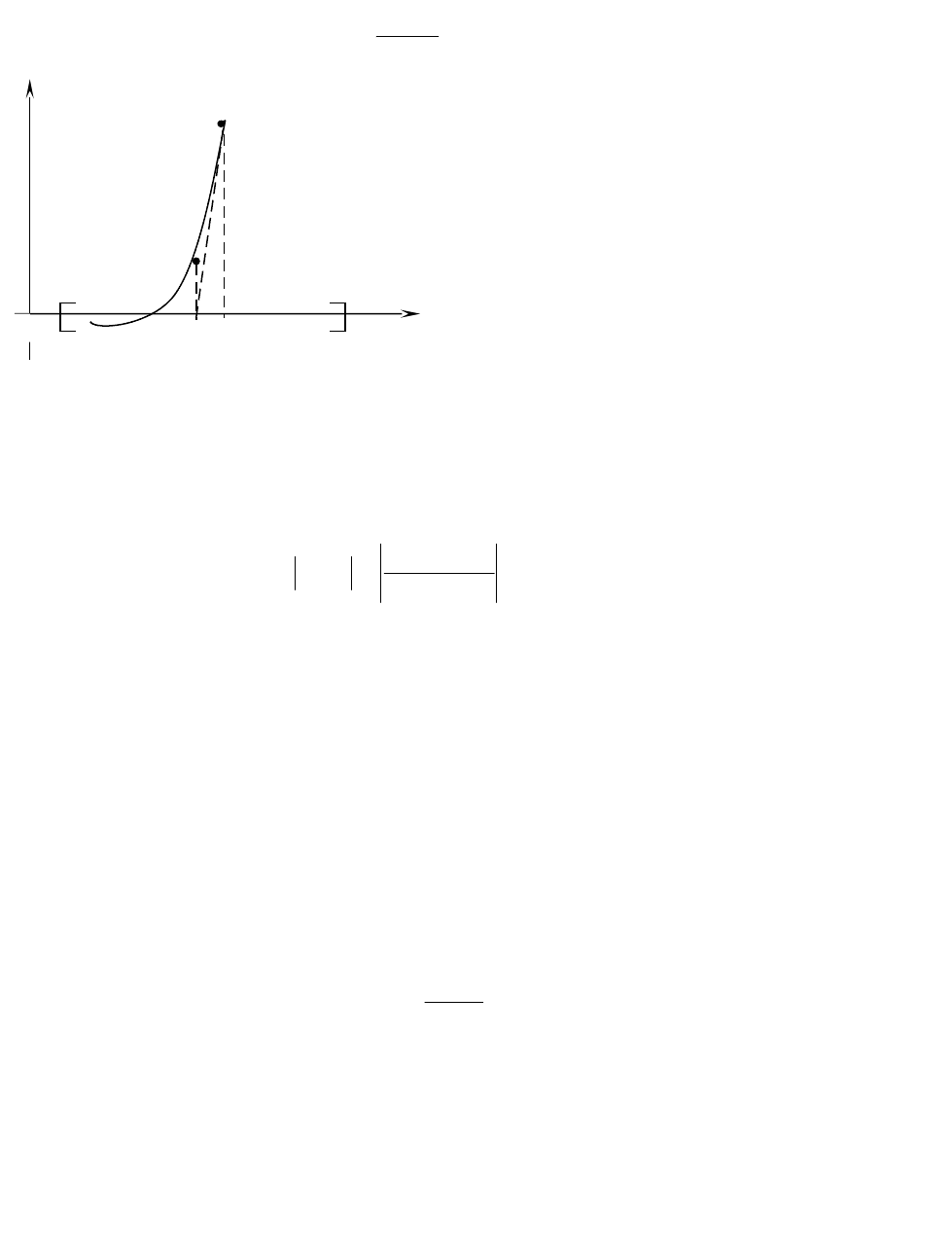
Для нахождения интервала

расположения корней воспользуемся

графическим методом. Для этого преобразуем

исходное уравнение к виду



и построим

два графика

ey 

xy 

(Рис.8). Абсцисса

точки пересечения этих графиков является

приближенным значением корня



. Более

точные значения можно получить по

итерационной формуле (3). Из рисунка видно,

что корень



находится на отрезке

]0,[a

. Выберем

1a

;

01)1(





0)0(

ef

. На концах отрезка функция

)(xf

меняет знак

0)( 



на

]0;1[

Запишем исходное уравнение в эквивалентном виде:

)()( xxecxx



где

]0;1[0

)(





. Выберем

1.0c

. Для получения корня процесс

итераций

 

xexx





1,0

сходится, так как

 

]0,1[11.09.0 



xexx

Таким образом, рабочая формула метода простых итераций будет иметь

вид:

xex

9,01,0





1.4. Метод Ньютона (метод касательных).

Пусть уравнение (1) имеет на интервале

 

ba,

единственный корень,

причем существует непрерывная на

 

ba,

производная

 



. Метод Ньютона

служит для уточнения корней нелинейных уравнений в заданном интервале.

Его можно рассматривать как частный случай метода простых итераций, если

 

x 



 )(

. Тогда итерационный процесс осуществляется по формуле:



ey 

xy 

Рис.8

 

,1,0,









(5)

Геометрически (Рис.9) этот процесс

означает замену на каждой итерации

графика кривой

)(xfy 

касательной к ней

в точках

),(

Достаточное условие сходимости

обеспечивается выбором начальной точки

. Начальным приближением

служит

один из концов отрезка

],[ ba

, в

зависимости от того, в каком из них

выполняется достаточное условие

сходимости

   





xfxf

(6)

При произвольном начальном приближении итерации сходятся, если

],[1

))((

)()(

)(

bax

xfxf

x 

Метод Ньютона рекомендуется применять для нахождения простых

действительных корней уравнения (1).

Достоинством метода является то, что он обладает быстрой скоростью

сходимости, близкой к квадратичной. Недостатки метода:

- не при любом начальном приближении метод Ньютона сходится, а лишь

при том, для которого

0)(





- если

 

0



, то



- если

 





, то

0

Последних трудностей можно избежать, применив модификацию метода

Ньютона, рабочая формула при этом имеет вид

 







2. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Система нелинейных уравнений имеет вид:

 













xxf



(7)

Здесь

xx ,,



- неизвестные переменные, а система (7) называется

нормальной системой порядка

, если хотя бы одна из функций

),...,(

1 ni

xxf

нелинейна.

Решение систем нелинейных уравнений – одна из трудных задач

вычислительной математики. Трудность состоит в том, чтобы определить:

имеет ли система решение, и, если – да, то сколько. Уточнение решений в

заданной области – более простая задача.



Рис.9

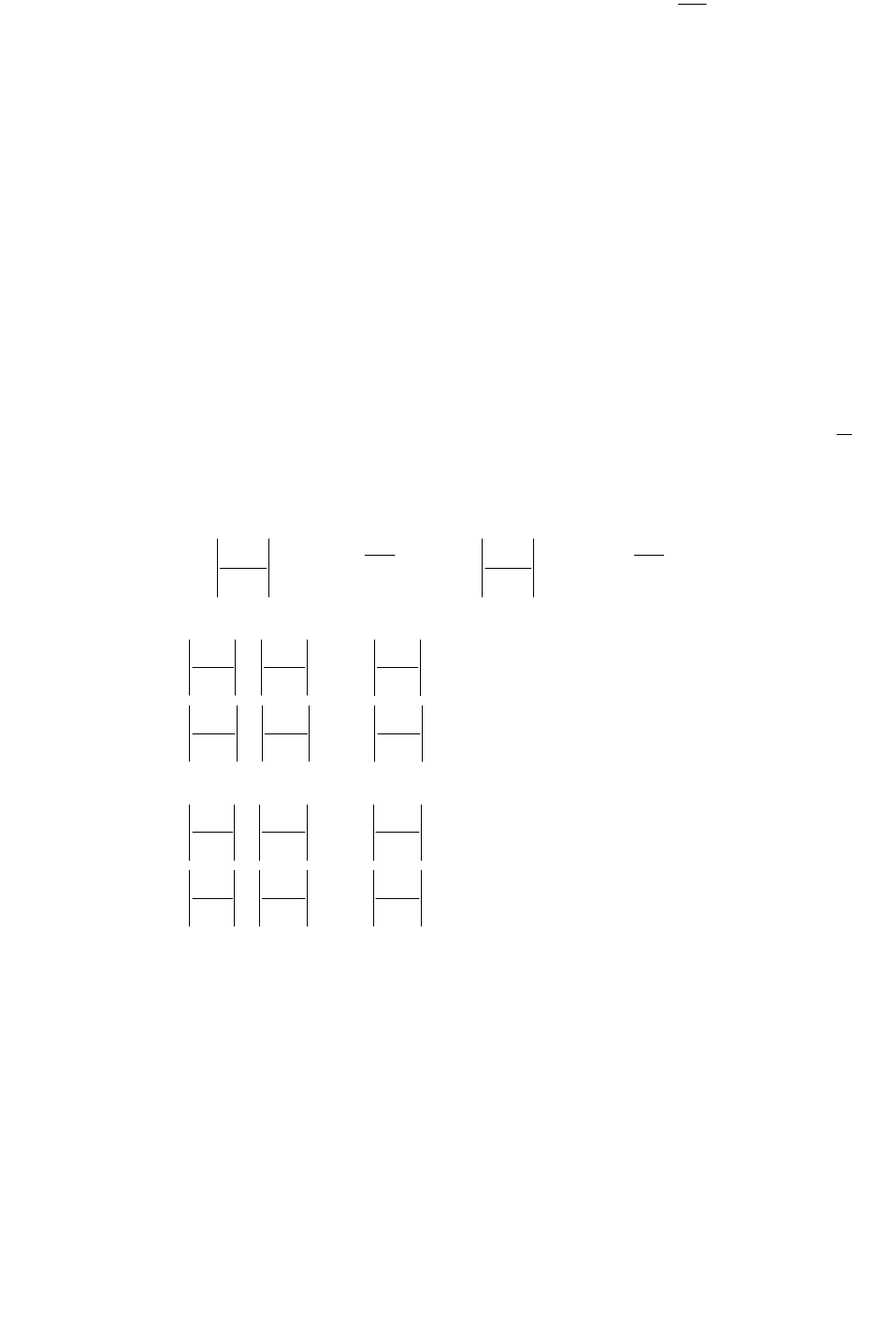
Пусть функции

определены в областях

,1, 

. Тогда область



1



и будет той областью, где можно найти решение. Наиболее

распространенными методами уточнения решения являются метод простых

итераций и метод Ньютона.

2.1. Метод простых итераций для решения систем нелинейных уравнений.

Из исходной системы (7) путем эквивалентных преобразований

переходим к системе вида:

 













nnn

xxx

111



(8)

Итерационный процесс, определяемый формулами

 















xxx



,1,0k

можно начать, задав начальное приближение

 



xxx 

Достаточным условием сходимости итерационного процесса является одно из

двух условий:

,1,1











или

,1,1











Распишем первое условие:



















xxx



при

1i



















nnn

xxx



при

ni 

Распишем второе условие:



















xxx



при

1j



















xxx



при

nj 

Рассмотрим один из способов приведения системы (7) к виду (8),

допускающему сходящиеся итерации.

Пусть задана система второго порядка вида:

 









yxf

Требуется привести ее к виду:

 









yxy

yxx

Умножим первое уравнение системы на неизвестную постоянную



второе - на



, затем сложим их и добавим в обе части уравнения

. Получим

первое уравнение преобразованной системы

   

;,,

xyxfyxfx 

где

     

yxfyxfxyx ,,,

211



Далее, умножим первое уравнение системы на неизвестную постоянную



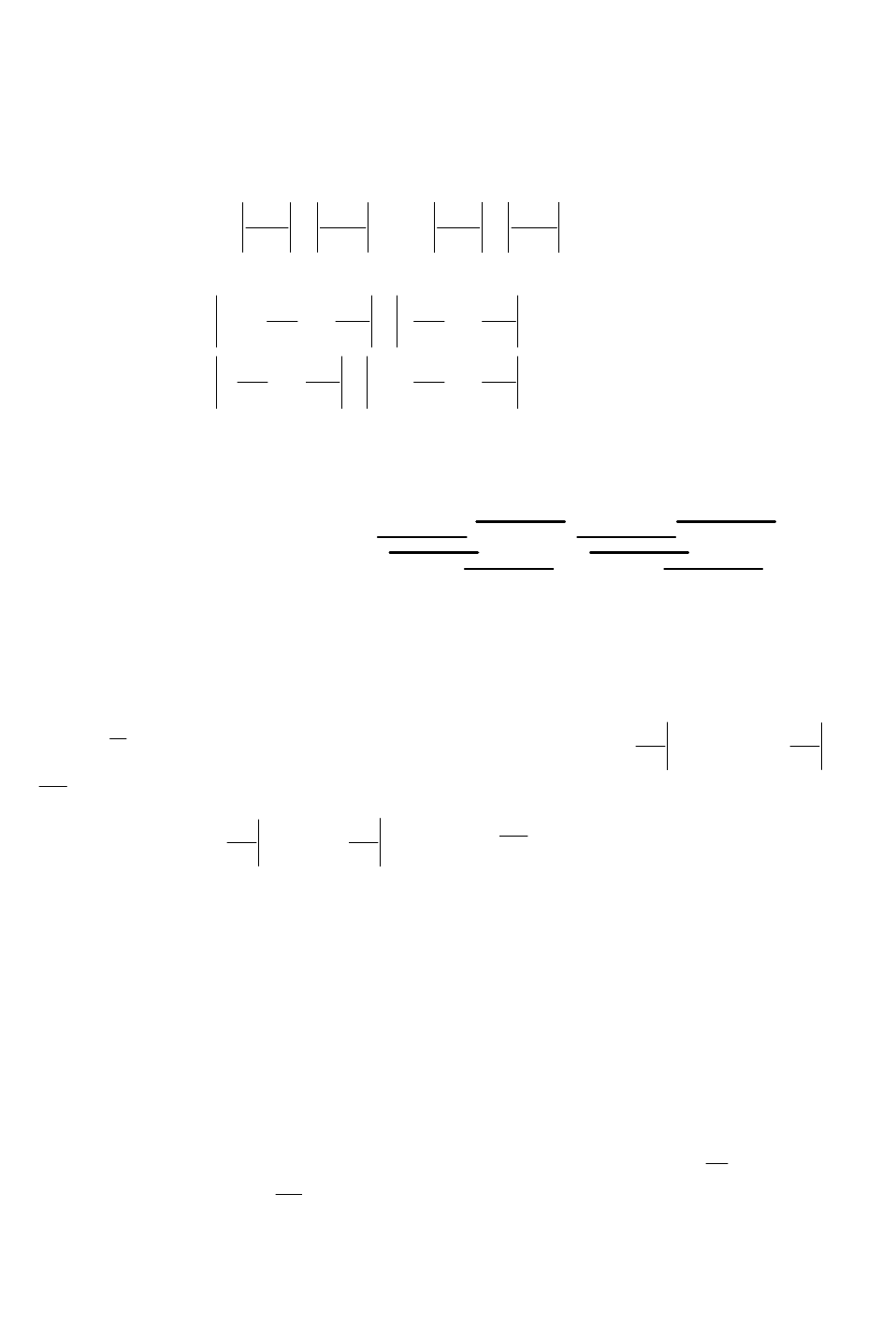
второе - на



, затем сложим их и добавим в обе части уравнения

. Тогда

второе уравнение преобразованной системы будет иметь вид

   

;,,

yyxfyxfy 

где

     

yxfyxfyyx ,,,

212



Неизвестные постоянные

 ,,,

определим из достаточных условий

сходимости

























Запишем эти условия более подробно:

2121



















2121



















Полагая равными нулю выражения под знаком модуля, получим систему

из четырех уравнений с четырьмя неизвестными для определения постоянных

 ,,,



















































При таком выборе параметров условия сходимости будут соблюдены,

если частные производные функций

),(

yxf

),(

yxf

будут изменяться не

очень быстро в окрестности точки

   

 

, yx

Чтобы решить систему, нужно задать начальное приближение

   

 



, yx

и вычислить значения производных

   

 

, yx



   

 

, yx



2,1i

в этой точке. Вычисление

 ,,,

осуществляется на каждом

шаге

итераций, при этом

   

 



   

 



2,1i

Метод простых итераций является самоисправляющимся, универсальным

и простым для реализации на ЭВМ. Если система имеет большой порядок, то

применение данного метода, имеющего медленную скорость сходимости, не

рекомендуется. В этом случае, используют метод Ньютона, который имеет

более быструю сходимость.

2.2. Метод Ньютона для решения систем нелинейных уравнений.

Пусть требуется решить систему нелинейных уравнений вида (7).

Предположим, что решение существует в некоторой области



, в которой все

функции

 

nixxf

,1,,,



непрерывны и имеют, по крайней мере, первую

производную. Метод Ньютона представляет собой итерационный процесс,

который осуществляется по определенной формуле следующего вида:

     

 

kkkk

xfxWxx

11 



(9)