Лекции по численным методам (34 часа)

где

 

   

 

k

n

k

n

xx

x

n

x

n

xx

k

ff

xW

,,

11

1

,,



















Трудности при использовании метода Ньютона:

- существует ли обратная матрица?

- не выходит ли

 

1k

x

за пределы области



?

Модифицированный метод Ньютона облегчает первую задачу.

Модификация состоит в том, что матрица вычисляется не в каждой точке, а

лишь в начальной. Таким образом, модифицированный метод Ньютона имеет

следующую формулу:

     

 

kkk

xfxWxx

011 



(10)

Но ответа на второй вопрос, модифицированный метод Ньютона не дает.

Итерационный процесс по формулам (8) или (10) заканчивается, если

выполняется следующее условие

   



 kk

xx

1

.

Достоинством метода Ньютона является его быстрая сходимость по

сравнению с методом простых итераций.

3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

Пусть дана система линейных алгебраических уравнений (СЛАУ) вида

nnnnn

nn

bxaxa



...

11

22121

11111



(11)

или в матричной форме

BAx 

. (12)

3.1. Метод простых итераций для решения систем линейных

алгебраических уравнений.

Рассмотрим решение этой системы методом простых итераций. Для

применения этого метода необходимо предварительно преобразовать систему

(12) к виду

 xx

, (13)

где матрица



такова, что выполнены достаточные условия сходимости

итерационного процесса :

ni

n

j

ij

,1,1

1









или

nj

n

i

ij

,1,1

1









.

Зададим произвольно начальный вектор приближения

 

0

x

и подставим

его в правую часть преобразованной системы уравнений. Получим первое

приближение

)1(

x

. Аналогично получим

,...,

)3()2(

xx

. Итак, итерационная

формула

   

,....2,1,0,

1





kxx

kk

(14)

или в координатной форме:

     

 

     

 

   

 

n

k

nnn

k

n

k

n

k

n

k

nn

kkk

k

nn

kkk

xxxx





...

2

1

22

2

22

1

21

1

2

11

2

12

1

11

1

(15)

осуществляет итерации по “совокупности координат”. Последовательность

векторов

,...,,

)2()1()0(

xxx

, полученных по этой формуле, сходится к решению,

если выполнены вышеприведенные достаточные условия сходимости.

Пусть

)(

lim

k

xx





, тогда, переходя к пределу в равенстве (14), имеем









)()1(

limlim

k

xx

или имеет место формула (13). Следовательно, вектор

x

- решение системы.

Если в исходной системе (12) преобладание диагональных элементов

nia

ii

,1, 

над остальными коэффициентами значительное, то сходимость

итерационного процесса обеспечена. В этом случае переход от исходной

системы (12) к виду (13) можно осуществить путем деления каждого уравнения

системы (12) на коэффициент

ii

a

, формирования столбца

),...,(

1 n

xxx 

в левой

части и переноса остальных членов в правую часть. Введем обозначения

nji

a

b

a

ii

i

ii

ij

,1,,, 

. Тогда

nixx

n

jij

jijii

,1,

,1









.

Рабочая формула итерационного процесса имеет в этом случае следующий вид:

,...2,1,0,,1,

1

)()1(













knixx

n

ji

j

k

jiji

k

i

Начальное приближенное решение можно взять произвольно, например,

равным столбцу свободных членов



)0(

x

. Далее последовательно получаются

приближения

,...,

)2()1(

xx

. Если для преобразованной системы (13) выполнено

по меньшей мере одно из достаточных условий сходимости, то процесс

итераций (14) сходится к единственному решению этой системы, независимо от

выбора начального приближения.

Для системы (12) метод итераций сходится, если выполнены неравенства

niaa

n

j

ijii

,1,||

1









, т.е. модули диагональных коэффициентов в каждом

уравнении больше суммы модулей всех остальных коэффициентов (не считая

свободных членов).

Итерационный процесс следует закончить, когда два последовательных

приближения близки между собой по норме

   











n

j

k

j

k

j

kk

xxxx

1

)()1(

, где



- заданная точность.

3.2. Метод Зейделя.

Более быструю сходимость метода простых итераций можно обеспечить,

если для каждой

i

-ой компоненты вектора решения

 

1k

приближения

использовать предыдущие компоненты от 1 до

1i

также

 

1k

приближения,

а остальные компоненты от

i

до

n

используются от предыдущего

k

-го

приближения. Такая модификация метода простых итераций носит название

«метода Зейделя». Запишем рабочие формулы метода Зейделя для каждой

компоненты:

       

     

 

   

 

n

k

nnn

k

n

k

n

k

n

k

nn

kkk

k

nn

kkk

xxxx









...

1

2

1

22

2

22

1

21

1

2

11

2

12

1

11

1

.

Первое и второе достаточные условия для сходимости метода простых

итераций будут одновременно достаточными и для процесса Зейделя.

При использовании итерационных методов для решения систем ошибка

вычислений в большинстве случаев эквивалентна некоторому ухудшению

очередного приближения. Это отразится только на числе итераций, а не на

точности окончательного результата.

4. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

Задача интерполяции функций возникает в тех случаях, когда:

- функция задана в виде таблицы, и необходимо знать значения функции

для промежуточных значений аргументов, расположенных в таблице между

узлами

nix

i

,0, 

, а также для аргументов, расположенных вне таблицы;

– известна лишь таблица функции и требуется определить ее

аналитическое выражение;

– известно аналитическое выражение функции, но оно имеет очень

сложный вид, вследствие чего возникает необходимость представления этой

функции в более простом виде. Например, при вычислении определенных

интегралов вида

 



b

a

dxxf

можно заменить подынтегральную функцию

 

xf

некоторой приближенной функцией

 

xP

в виде многочлена. Тогда

   







b

a

b

a

dxxPdxxf

.

Построив интерполяционный многочлен любого вида также можно

расширить таблицу как влево, так и вправо, вычисляя построенный многочлен в

точках, не принадлежащих таблице (задача экстраполяции). Кроме того,

построив интерполяционных многочлен, можно уплотнить таблицу, определяя

значения функции для промежуточных аргументов между узловыми точками.

4.1. Интерполяционная формула Лагранжа.

Пусть задана система точек

nix

i

,0, 

, в которых известны значения

функции

 

nixfy

ii

,0, 

. То есть, задана следующая таблица

i

x

0

x

1

x

…

n

x

i

y

0

y

1

y

…

n

y

Установим зависимость

 

xy

одного ряда чисел от другого и построим

новую функцию, которая с определенной степенью точности будет приближена

к заданной.

Рассмотрим пример построения интерполяционного многочлена

Лагранжа по заданной системе точек (в общем случае для неравноотстоящих

аргументов). Построим некоторый многочлен

 

xP

n

таким образом, чтобы его

значения совпали со значениями функции, заданными в таблице, для тех же

аргументов, то есть

 

niyxP

iin

,0, 

. Лагранж предложил строить многочлен

n

степени в виде:

              

1020110 



nnnnn

xxxxaxxxxxxaxxxxaxP 

.

Здесь в каждом слагаемом отсутствует скобка

 

i

xx 

, которой

соответствует коэффициент

i

a

.

Найдем неизвестные коэффициенты

nia

i

,0, 

, называемые

коэффициентами Лагранжа, используя условие

 

niyxP

in

,0, 

:

При

0

xx 

:

 

00

yxP

n



.

      

00201000

yxxxxxxaxP

nn

 

.

Следовательно, коэффициент

0

a

вычисляется по следующей формуле:

    

n

xxxxxx

y

a





02010

0



При

1

xx 

:

 

11

yxP

n



.

      

11210111

yxxxxxxaxP

nn

 

.

Следовательно, коэффициент

1

a

вычисляется по следующей формуле:

    

n

xxxxxx

y

a





12101

1



.

Значения остальных коэффициентов вычисляются аналогично.

С учетом найденных коэффициентов интерполяционный многочлен

Лагранжа запишется в виде

 

    

   

    

   

10

110

010

21

0















nnn

n

xxxx

xxxxxx

y

xxxx

xxxxxx

yxP



Остаточный член формулы:

))...((

)!1(

)(

0

1

n

xxxx

n

f

xR 









,

где



- точка наименьшего промежутка, содержащего все узлы

nix

i

,0, 

и

точку

x

.

Пример. По заданной системе точек

i

x

524.0

6





785.0

4





571.1

2





i

y

0.5 0.707 1.0

построить интерполяционный многочлен Лагранжа второго порядка вида:

          

1022012102

xxxxaxxxxaxxxxaxP 

Коэффициенты этого многочлена будут вычислены по формулам вида:

  

824.1

)571.1524.0)(785.0524.0(

5.0

2010

0











xxxx

y

a

  

439.3

)571.1785.0)(524.0785.0(

707.0

2101

1











xxxx

y

a

  

216.1

)785.0571.1)(524.0571.1(

1

1202

2











xxxx

y

a

Тогда многочлен Лагранжа второго порядка будет иметь вид:

))((216.1))((439.3))((824.1)(

1020212

xxxxxxxxxxxxxP 

.

Учитывая, что таблица приведена для функции

)sin(xy 

, вычисленной в

контрольных точках

2

,

4

,

6



, сравним погрешность вычислений данной

функции и построенного многочлена в контрольной точке

3



:

866.0

2

3

sin

3

































y

и

859.0)

3

(

2





P

.

Погрешность вычислений, по сравнению с истинным значением,

составляет

007.0859.0866.0)

3

()

3

sin(

2









P

.

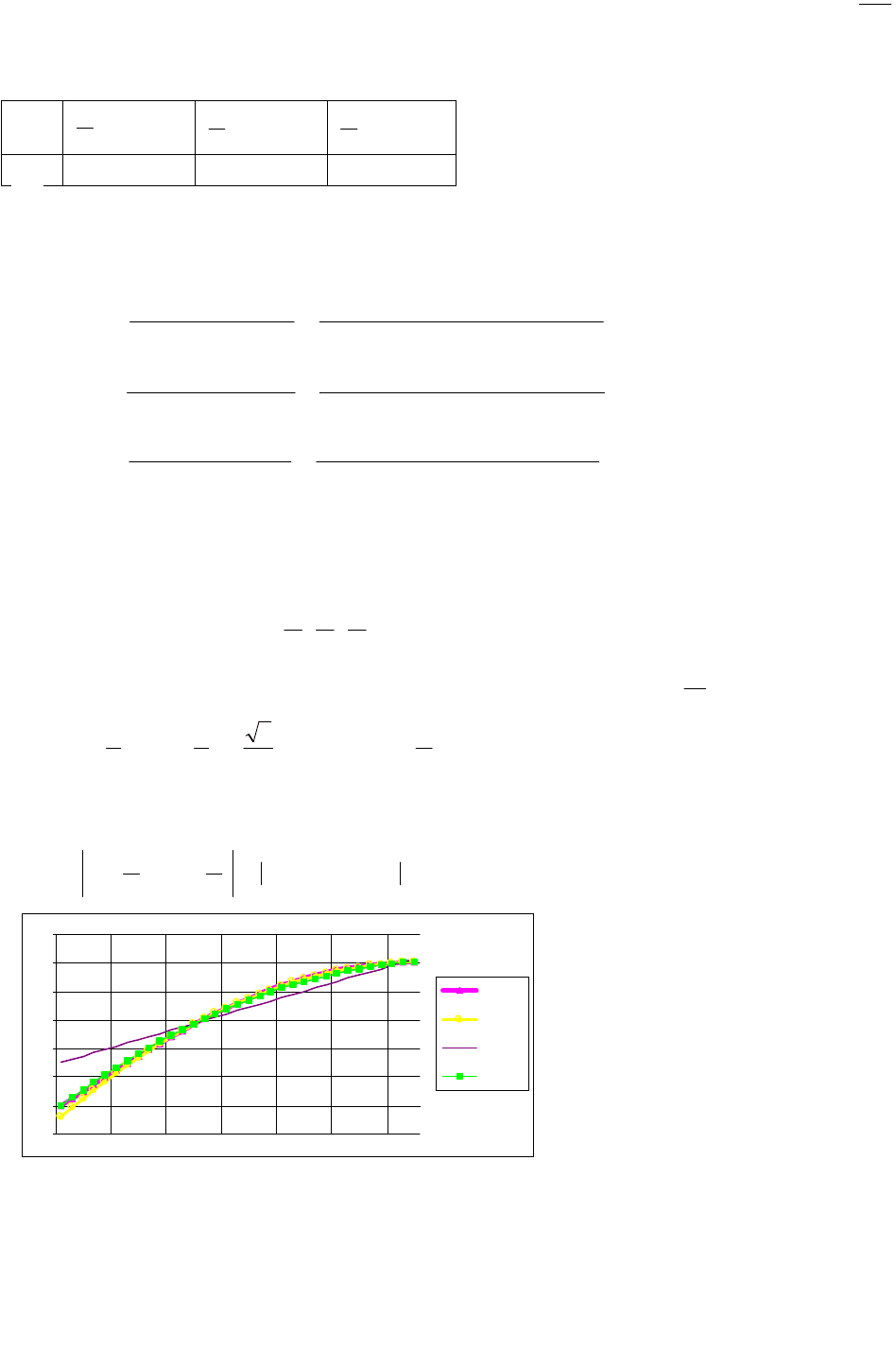
Ниже приведены графики

синусоиды и построенного

многочлена Лагранжа на

заданном интервале. Из

графика видно, что многочлена

второго порядка достаточно

для обеспечения необходимой

точности воспроизводимой

синусоиды.

4.2. Первая интерполяционная формула Ньютона.

Если таблица, для которой построена формула Лагранжа, задана для

равноотстоящих узлов

hxx

ii



1

, то формула Лагранжа упрощается.

-0,2

0

0,2

0,4

0,6

0,8

1

1,2

0 0,25 0,5 0,75 1 1,25 1,5

sin(x)

L2(x)

P1(x)

P2(x)

Обозначим через

 

h

xx

t

0





. Тогда

 

11

00

1













t

h

xx

h

hxx

h

xx

;

2





t

h

xx

;…,

it

h

xx

i





.

С учетом введенных обозначений формула Лагранжа запишется так:

 

    

   

     

    

 

11

121

2

21

10





















nn

nttt

y

n

nttt

y

n

nttt

yxP

n

.

Запишем формулу Лагранжа в случае, если

1n

:

00010100

10

01

0

1

10

1

01

)(

)1(

)(

ytyyytytytyy

tyty

xx

y

xx

yxP













.

Получили формулу линейной интерполяции вида.

 

001

ytyxP 

.

Здесь

,...2,1,

1





iyyy

iii

- табличные разности первого порядка.

При

2n

получаем формулу квадратичной интерполяции вида

 

0

2

002

2

1

y

tt

ytyxP 





.

Здесь

,...2,1,

1

2





iyyy

iii

- табличные разности второго порядка.

Таким образом, первая интерполяционная формула Ньютона будет иметь

вид:

 

      

00

2

00

!

11

!2

1

y

n

nttt

y

tt

ytyxP

n













.

Остаточный член формулы имеет вид:

)(

)!1(

))...(1(

)(

11









 nn

n

f

n

nttt

hxR

, где

)(

11

0

1



 nnn

fhy

,



- точка наименьшего промежутка, содержащего все узлы

nix

i

,0, 

и точку

x

. Первая интерполяционная формула рекомендуется для интерполяции в

начале таблицы.

4.3. Вторая интерполяционная формула Ньютона.

Вторая интерполяционная формула Ньютона используется при

вычислении функции для значений

x

, близких к концу таблицы и для

продолжения таблицы. Обозначим через

h

xx

t

n





, тогда

11

)(

1













t

h

xx

h

hxx

h

xx

nnn

. Тогда получим следующую формулу

Ньютона:

02

2

1

!

)1)...(1(

...

!2

)1(

)( y

n

nttt

y

tt

ytyxP

n

nnnn













.

Погрешность формулы

)(

)!1(

))...(1(

)(

11









 nn

n

f

n

nttt

hxR

имеет тот же

смысл, что и в первой формуле Ньютона.

4.4. Применение интерполяционных многочленов для приближенного

вычисления производных функции.

Интерполяционные многочлены могут быть использованы для

приближенного вычисления первой, второй и производных других порядков

для функций, заданных таблицей или для функций, имеющих сложный

аналитический вид. При этом погрешность будет достаточно велика даже для

нахождения первой производной. Проблема состоит в том, что значения

многочлена

)(xP

n

и функции

)(xf

в узловых точках совпадают, но значения

производных в них не совпадают, т.е. тангенсы углов наклона в каждой точке

не равны.

Значения производных в узловых точках, заданных в таблице,

приближенно можно вычислить по формулам вида:

...;

22

;

0

2

12

'

1

001

'

0

h

y

h

yy

y

h

y

h

yy

y

















Более точные значения производных можно получить, если

предположить, что

)()(

'

xPxf

n





. Тогда получим:

 

    

...

!3

263

!2

12

...

!3

21

!2

1

0

3

2

0

2

0

3

0

2

00









































y

h

tt

y

h

t

h

y

ttt

y

tt

ytyxP

n

.

Аналогично можно получить

))(()(







xPxP

nn

и т.д.

4.5. Численное интегрирование. Квадратурная формула Ньютона-Котеса.

Если функция

 

xf

непрерывна на отрезке

 

ba,

и известна ее

первообразная

 

xF

, то определенный интеграл от этой функции в пределах от

a

до

b

может быть вычислен по формуле Ньютона-Лейбница:

     

aFbFdxxf

b

a





(16)

где

   

xfxF 



. Однако, во многих случаях

 

xF

не может быть найдена с

помощью элементарных средств или является слишком сложной; вследствие

этого вычисление определенного интеграла по формуле (16) может быть

затруднено или даже практически невыполнимо. Поэтому, важное значение

приобретают численные методы вычисления определенных интегралов,

использующие ряд значений подынтегральной функции в точках

 

bax

i

,

.

Вычисление однократного интеграла называется механической

квадратурой, двойного - механической кубатурой. Соответствующие формулы

будем называть квадратурными и кубатурными формулами.

Рассмотрим способы вычисления однократных интегралов.

Если воспользоваться интерполяционным полиномом Лагранжа, то,

заменяя функцию

 

xf

полиномом

 

xP

n

, получим равенство

   

 







b

a

nn

b

a

fRdxxPdxxf

(17)

где

 

fR

n

- ошибка этой квадратурной формулы.

Пусть требуется вычислить интеграл



b

a

ydx

, где

 

nixfyxfy

ii

,0),(, 

.

Выбрав шаг

n

ab

h





, разобьем отрезок

 

ba,

на

n

равных частей с помощью

равноотстоящих точек

ax 

0

,

ihxx

i



0

,

1,1  ni

,

bx

n



. Заменим

подынтегральную функцию интерполяционным полиномом Лагранжа

)(xP

n

и

получим приближенную квадратурную формулу





















n

i

ii

x

n

i

ii

b

a

n

b

a

b

a

yAdxyxa

dxxPydxdxxf

n

00

0

)(

;)()(

(18)

Выведем явные выражения для коэффициентов

i

A

формулы (18).

Многочлен Лагранжа

   





n

i

iin

yxaxP

0

имеет коэффициенты

 

       

niiiiiii

nii

i

xxxxxxxxxx

xa









1110

,

ni ,0

.

Вводим обозначения

h

xx

q

0





и

 

   

nqqqq

n





1

1

и с учетом этих

обозначений многочлен Лагранжа запишем в виде:

 

 

i

n

i

n

in

n

y

iq

q

ini

xP















0

1

!!

1

(19)

Заменяя в формуле (18) функцию

)(xf

полиномом

 

xP

n

в виде (19),

получим:

 

 





















n

i

ii

x

i

n

i

n

in

yAdxy

iq

q

ini

n

00

1

0

!!

1

,

где

 

 















n

x

n

in

i

dx

iq

q

ini

A

0

1

!!

1

.

Так как

h

xx

q

0





и

h

dx

dq 

, то сделав замену переменных в

определенном интеграле, будем иметь:

 

 













n

in

i

dq

iq

q

ini

hA

0

1

!!

1

,

ni ,0

.

Так как

n

ab

h





, то можно записать коэффициенты Котеса:

 

 

dq

iq

q

nin

H

n

in

i















0

1

!1!

11

,

ni ,0

(20)

Квадратурная формула при этом принимает вид:

 









n

i

ii

b

a

yHabydx

0

(21)

Рассмотрим частные случаи.

По формуле (20) при

1n

вычислим:

 

2

1

0





 dqqH

,

2

1

0

1





 qdqH

)(

2

10

1

0

yy

h

ydx

x





.

Полученная формула является формулой трапеций для приближенного

вычисления определенного интеграла (Рис.10).

По формуле (20) при

2n

вычислим:

  

0,

6

1

46

3

8

4

1

21

2

1

2

1

2

0



















 idqqqH

 

1,

3

2

1

2

1

2

0

1





 idqqqH

;

 

2,

6

1

2

1

2

1

2

0

2





 idqqqH

.

Следовательно, так как

hxx 2

02



, то квадратурная формула для вычисления

интеграла имеет вид

)4(

3

210

2

0

yyy

h

ydx

x





.

Эта формула является формулой Симпсона. Геометрическая

интерпретация формулы состоит в том, что происходит замена данной кривой

 

xfy 

параболой

 

xLy

2



, проходящей через три точки

210

,, MMM

(Рис.11).

 

xfy 

x

y

1

x

1

y

0

y

0

x

h

Рис.10

x

y

2

x

1

y

0

y

0

x

Рис.11

1

x

2

y

 

xfy 

 

xLy

2



1

M

2

M

0

M

4.7. Метод наименьших квадратов для обработки результатов

экспериментов.

Данный метод относится к классу аппроксимационных методов. Идея

метода состоит в том, чтобы по данным эксперимента построить приближенно

функцию, отображающую зависимость ее от

x

, в виде многочлена с тем

расчетом, чтобы сумма квадратов отклонений построенной функции от

экспериментальной в узловых точках была минимальна. Будем строить

функцию в виде многочлена

 

01

1

axaxaxaxf

n







.

Используем для построения результаты эксперимента, заключенные в

таблице

i

x

0

x

1

x

…

m

x

i

y

0

y

1

y

…

m

y

Построить многочлен, значит, определить его коэффициенты

nia

i

,0, 

.

Для этого введем функцию







m

i

S

0

2

и потребуем, чтобы







m

i

S

0

2

minmin

, где

 

iii

yxf 

- отклонение функции от экспериментальной в узлах

mix

i

,0, 

.

Используя вид

)(xf

, получим:

 





















m

i

n

in

n

in

aaaaa

yaxaxaS

nn

0

2

0

1

,,,...,,

010

minmin 



.

Необходимыми условиями экстремума функции

S

является равенство

нулю ее первой производной по всем переменным

0;0;0

10













n

a

S

a

S

a

S



.

Расписав эти условия, получим СЛАУ вида:

 





































m

i

n

ii

n

in

n

in

n

m

i

ii

n

in

n

in

m

i

n

in

n

in

xyaxaxa

a

S

xyaxaxa

a

S

yaxaxa

a

S

0

1

0

1

0

1

0

02

..............................................................................

02



Запишем систему для определения

n

aa ,,

0



в нормальной форме:































m

i

n

i

m

i

n

i

m

i

n

i

m

i

n

i

m

i

ii

m

i

n

i

m

i

m

i

m

i

m

i

n

i

m

i

m

i

yxaxaxax

yaxaxaxma

00

2

0

1

0

00

1

0

1

2

0

000

2

0

10



Решаем систему одним из известных методов и находим

n

aa ,,

0



,

которые затем подставляем в искомый многочлен.

Запишем алгоритм метода наименьших квадратов.

1. Вводим таблицу чисел

miyx

ii

,0,, 

.

2. Вычисляем





m

i

n

i

m

i

ii

m

i

m

i

n

i

m

i

m

i

m

i

yxyxyxxxx

0000

2

0

3

0

2

0

,,,,,,,, 

.

3. Решая любым известным методом полученную систему линейных

алгебраических уравнений, находим

n

aa ,,

0



- коэффициенты искомого

многочлена.

Лекции по численным методам (34 часа)

Подождите немного. Документ загружается.