Лекции - Математические модели и численные методы в динамике жидкости и газа

Подождите немного. Документ загружается.

9.9. Задача диффузии аргона и гелия 201

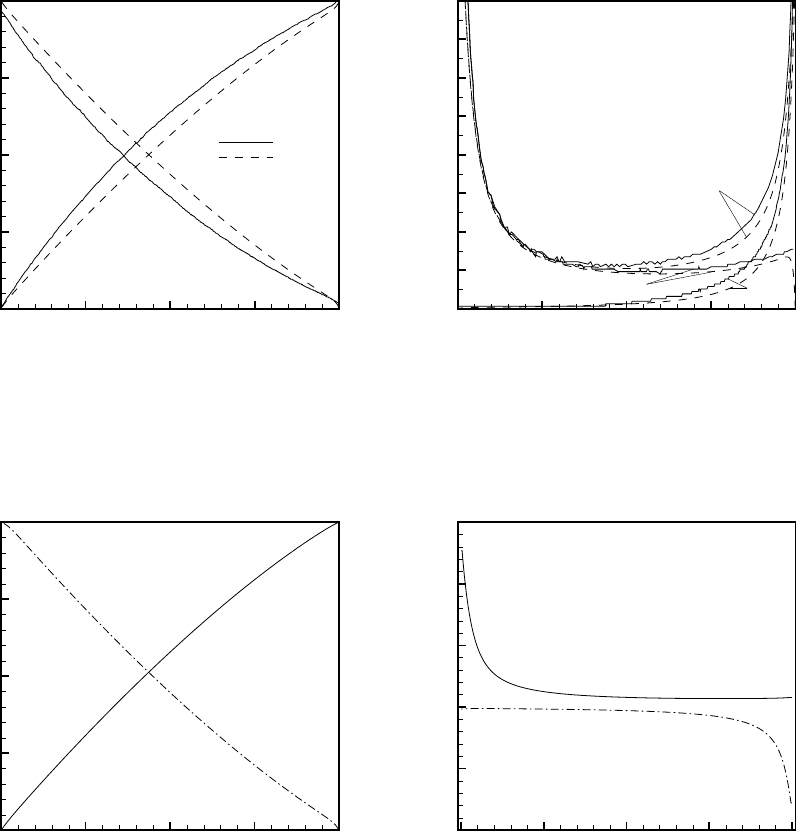
смещается от середины области влево, ближе к разервуару с более тяже-

лым газом. Скорость диффузии гелия больше, чем аргона, качественное

поведение скоростей диффузии компонент различно: скорость диффузии

гелия имеет слабо выраженный минимум в середине расчетной области.

На рис. 9.8 приведены распределения давлений и скоростей компонент

между резервуарами. Распределение давлений повторяет распределение

числовых плотностей (рис. 9.8 слева). Скорость каждой из компонент

очень мала вблизи резервуара с этой компонентой, и значительно воз-

растает вблизи противоположного резервуара (рис. 9.8 справа).

0.25 0.5 0.75

x (m)

0.25

0.5

0.75

number density

DSMC

QGDM

0 0.25 0.5 0.75 1

x (m)

100

120

140

160

diffusion velocity (m/s)

-Ud

Рис. 9.7: Числовая плотность (слева) и диффузионные скорости (справа) в смеси

Ar-He

0 0.25 0.5 0.75 1

x/Lambda

0.25

0.5

0.75

Normalized value

0 0.25 0.5 0.75 1

x/Lambda

-0.1

0.1

0.2

0.3

Normalized value

Рис. 9.8: Давления (слева) и скорости (справа) компонент в смеси Ar-He

202 Глава 9. КГДМ уравнения для бинарной смеси газов

9.10 Заключение

На основе системы кинетических уравнений в релаксационном прибли-

жении построена макроскопическая система КГДМ уравнений, которая

описывает течение смеси нереагирующих газов. В отличие от ряда ши-

роко известных моделей, КГДМ система состоит из уравнений для плот-

ности, импульса и энергии для каждой из компонент, то есть является

двухжидкостным приближением, что позволяет детально описывать по-

ведение каждой из компонент.

Уравнения для импульса и энергии включают в себя обменные члены,

что учитывает соответствующие обмены между компонентами газовой

смеси. Для вычисления этих слагаемых требуется определить частоту

взаимных столкновений молекул обоих сортов. КГДМ модель включает

в себя также и диффузионые процессы, для описания которых требуется

знание коэффициента вязкости смеси. При этом не требуется отдельно

вычислять коэффициенты термо, баро и самодиффузии, которые вклю-

чают в себя традиционные модели и определение которых представляет

собой самостоятельную задачу.

Выписано одножидкостное приближение для КГДМ уравнений и про-

слежена его связь с традиционной системой уравнений типа Навье–

Стокса в этом приближении. Показано, что обе одножидкостные моде-

ли бизки между собой, хотя и оказываются заметно менее точными по

сравнению с двухжидкостным КГДМ приближением и, тем более, с эта-

лонными результатами метода DSMC.

Несмотря на использование в приведенных расчетах достаточно про-

стой модели для вязкости смеси и частоты взаимных столкновений ча-

стиц, КГДМ модель достаточно точно описывает течение даже если мо-

лекулы в смеси сильно отличаются по массе. Для дальнейшего усовер-

шенствования КГДМ модели можно использовать более точные выраже-

ния для обоих коэффициентов переноса, входящих в КГДМ уравнения.

Система КГДМ уравнений записывается в инвариантном виде, что

позволяет использовать ее для решения задач в разнообразных простран-

ственных постановках. В вычислительном плане алгоритмы, построен-

ные на основе КГДМ модели, оказываются более устойчивыми, чем ана-

логичные алгоритмы, построенные на основе традиционных уравнений

сохранения типа уравнений Навье–Стокса.

Модель допускает обобщения на произвольное число компонент, так

9.10. Заключение 203

как смесь из нескольких компонент можно представить как суперпози-

цию бинарных смесей. Возможно включение в модель химических реак-

ций между компонентами.

Заключительные замечания

Уравнения динамики газа и жидкости могут быть выписаны на осно-

ве интегральных законов сохранения массы, импульса, энергии, момен-

та импульса и второго закона термодинамики (в форме интегрального

уравнения для энтропии). Для замыкания уравнений сохранения можно

использовать различные гипотезы для определения газодинамических

параметров.

Если определять газодинамические параметры как пространственные

средние, то придем к системе уравнений Навье-Стокса. При построении

КГД систем используется другое определение газодинамических вели-

чин. Они определяются как пространственно-временные средние. При

этом вектора плотности потока массы, тепловой поток и тензор вязких

напряжений для КГД уравнений отличаются от соответствующих вели-

чин для уравнений Навье-Стокса дополнительными слагаемыми с малым

коэффициентом, имеющим размерность времени. Характер уравнений

остается диссипативным.

Каждой из двух КГД систем соответствует свой способ решения про-

блемы замыкания. Квазигазодинамические уравнения следует использо-

вать только при моделировании течений идеального политропного газа,

а квазигидродинамические — при исследовании движений неидеальных

газов и жидкостей. При численном моделировании вязких течений до-

полнительные слагаемые проявляют себя как эффективные регуляриза-

торы.

В стационарном случае обе КГД системы отличаются от уравнений

Навье–Стокса (и друг от друга) дивергентными членами, имеющими

формальные асимптотические порядки малости O(Kn

) при Kn → 0.

Влияние добавочных членов незначительно для стационарных и квази-

стационарных газодинамических течений при малых числах Кнудсена.

Однако для сильно нестационарных течений, а также при числах Kn,

близких к единице, их вклад становится существенным. Именно в этом

классе задач следует искать преимущества новых моделей.

КГД системы отличаются от других систем, которые в разное время

предлагались в работах [31], [32], [33], [34], [35]. Уравнения КГД принци-

пиально отличаются от уравнений Барнетта [11], [14]. Уравнения Барнет-

та представляют собой уравнения, отличающиеся от уравнений Навье-

204

Заключительные замечания 205

Стокса дополнительными производными третьего порядка по простран-

ству. Эти добавки имеют дисперсионный характер. Добавки в КГД урав-

нениях имеют вид вторых производных по пространству и носят дисси-

пативный характер.

Вопрос о границах применимости КГД моделей является одним из

наиболее сложных. Чтобы ответить на него, необходимы дополнитель-

ные исследования.

К настоящему времени на основе КГД уравнений проведено численное

моделирование разнообразных течений газа и жидкости. Помимо задач,

описанных в предыдущих главах, имеется целый ряд других решенных

задач. В частности, детальное сравнение результатов, полученных на ос-

нове подходов Навье-Стокса, КГД и DSMC проводилось для задач о те-

чении в окрестности пластины [119], диска [125] и полого цилиндра [121].

Решалась задача о течении в недорасширенной струе [22], [23], рассчи-

тывалась структура ударной волны [24], [39], [40]. Последние результаты

сопоставялись с экспериментами [38]. Рассматривалась задача о течении

газа в микроканале [61]. КГД уравнения оказались очень эффективны-

ми для расчетов нестационарных течений газа, среди которых укажем

[62], [81], [126], [127]. Построены и опробованы в численном эксперименте

модификации КГД уравнений для описания течений электропроводных

сред [128], [129]. Предпринимаются попытки расчета турбулентных тече-

ний на основе КГД моделей [130], [131].

Эти и многие другие результаты численного моделирования, выпол-

ненные на основе КГД уравнений указывают на перспективность этих

новых систем уравнений и возможность их использования для расчетов

практических задач газо и гидродинамики.

Приложение. Построение КГД уравнений

для плоского одномерного течения

В качестве примера приведем детальный вывод квазигазодинамической

системы уравнений для случая плоского одномерного течения вдоль оси

x. При этом скорости молекул

ξ = (ξ

, ξ

, ) связаны с тепловыми ско-

ростями ~c = (c

, c

) соотношениями

= u + c

, ξ

= c

, ξ

= c

где u - макроскопическая скорость течения газа вдоль оси x. В этом

случае модельное кинетическое уравнение принимает вид

∂f

∂t

+ ξ

∂f

∂x

− ξ

∂

∂x

τξ

∂f

∂x

= I. (9.10.1)

Макроскопические уравнения строятся путем умножения уравнения

(9.10.1) последовательно на сумматорные инварианты

ξ) = 1, ξ

и осреднения по всем скоростям частиц

ξ. Законы сохранения массы,

импульса и энергии в процессе столкновений выражаются следующим

соотношением для интеграла столкновений

Ih(

ξ)d

ξ = 0. (9.10.2)

Таким образом, из результирующих уравнений исчезают слагаемые с ин-

тегралом столкновений.

Уравнение неразрывности

Интегрируем уравнение (9.10.1) по всем скоростям частиц. При интегри-

ровании первого слагаемого получаем

∂f

∂t

ξ =

∂

∂t

ξ =

∂ρ

∂t

Второе слагаемое преобразуется как

∂f

∂x

ξ =

∂

∂x

(u + c

) f

ξ =

∂

∂x

u f

ξ =

∂

∂x

ρu. (9.10.3)

206

Уравнение импульса 207

Здесь использованы соотношения (3.2.3) в виде

ξ = 0, (9.10.4)

совместно с определением ρ

ρ =

ξ =

ξ.

Второе слагаемое в левой части уравнения (9.10.1) преобразуется как

∂

∂x

(τξ

∂f

∂x

) d

ξ =

∂

∂x

∂

∂x

∂

∂x

∂

∂x

(u + c

)

∂

∂x

∂

∂x

(ρu

+ p). (9.10.5)

Здесь использованы соотношения (3.2.3) и (9.10.4) совместно с определе-

нием давления p в виде

p =

ξ =

+ c

ξ =

ξ. (9.10.6)

Объединяя выражения (9.10.2), (9.10.3) и (9.10.5), получим первое

уравнение КГД системы в виде

∂ρ

∂t

∂ρu

∂x

∂

∂x

∂

∂x

(ρu

+ p). (9.10.7)

Уравнение импульса

Умножим уравнение (9.10.1) на ξ

и проинтегрируем по всем скоростям

ξ.

Принимая во внимание определение плотности и (3.2.3), (9.10.4) и

(9.10.6), запишем первое и второе слагаемые кинетического уравнения

как

∂f

∂t

ξ =

∂

∂t

ξ =

∂

∂t

ρu,

∂

∂x

ξ =

∂

∂x

+ 2 c

u + c

) f

ξ =

∂

∂x

(ρu

+ p). (9.10.8)

208 Приложение. Построение КГД уравнений для плоского одномерного течения

Последнее слагаемое преобразуется следующим образом:

∂

∂x

τ ξ

∂f

∂x

ξ =

∂

∂x

∂

∂x

ξ =

∂

∂x

∂

∂x

(u + c

)

∂

∂x

∂

∂x

+ 3 u

+ 3 uc

+ c

) f

∂

∂x

∂

∂x

(ρu

+ 3 pu). (9.10.9)

Здесь использованы выражения (3.2.3), (9.10.4) и (9.10.6) совместно с

формулой

ξ = 0. (9.10.10)

В более общем случае вследствие симметрии справедливо соотноше-

ние

ξ = 0. (9.10.11)

Объединяя уравнения (9.10.2), (9.10.8) и (9.10.9), получим второе

уравнение КГД системы в виде

∂

∂t

ρu +

∂

∂x

(ρu

+ p) =

∂

∂x

∂

∂x

(ρu

+ 3 pu). (9.10.12)

Уравнение энергии

Осредняя уравнение (9.10.1) с весом

/2 получим для первых двух сла-

гаемых модельного кинетического уравнения

+ ξ

ξ =

∂E

∂t

∂

∂x

+ ξ

ξ =

∂

∂x

+ ξ

ξ +

∂

∂x

+ u)

+ c

ξ =

∂

∂x

uE +

∂

∂x

up. (9.10.13)

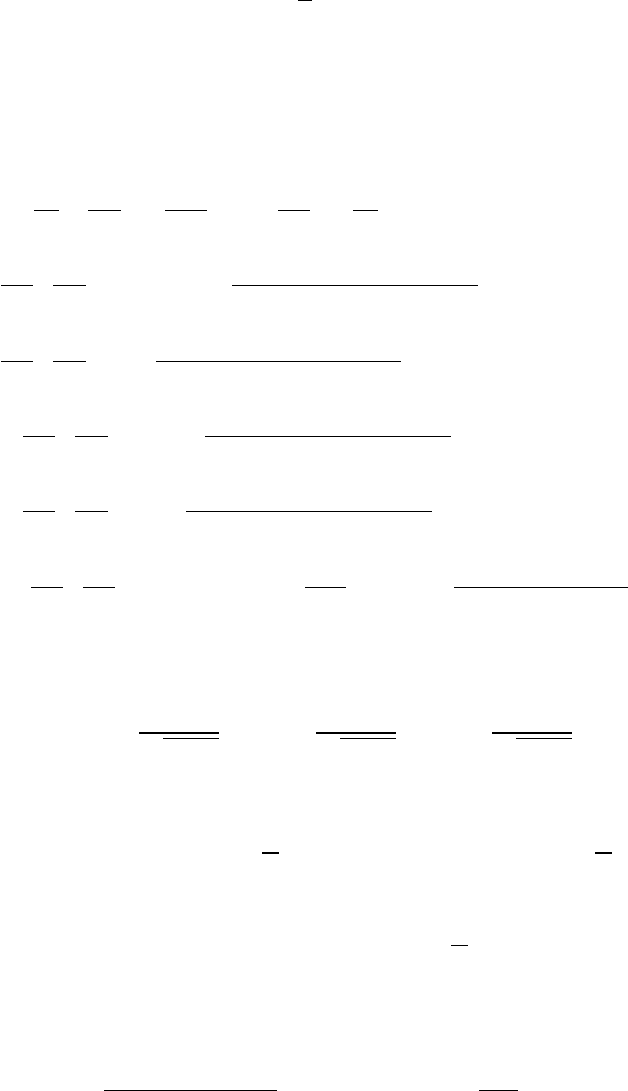
Уравнение энергии 209

Здесь мы использовали определения для ρ и p совместно с уравнени-

ями (9.10.11) и определение полной энергии в виде

E =

ξ. (9.10.14)

Последнее слагаемое кинетического уравнения преобразуется в слага-

емое диссипативного типа в уравнении для полной энергии

∂

∂x

τξ

∂f

∂x

ξ =

∂

∂x

ξ =

∂

∂x

∂

∂x

(u + c

)

+ u)

+ c

ξ =

∂

∂x

∂

∂x

+ u)

+ c

∂

∂x

∂

∂x

2uc

+ u)

+ c

∂

∂x

∂

∂x

+ u)

+ c

∂

∂x

∂

∂x

E + 2u

p +

+ c

ξ).

Для вычисления последнего интеграла сделаем замену переменных

x =

√

2RT

, y =

√

2RT

, z =

√

2RT

Принимая во внимание формулы

exp (−x

)dx =

√

π,

exp (−x

)dx =

√

π/2,

exp (−x

)dx = 3

√

π/4,

получим

+ c

2ρ

. (9.10.15)

В соответствии с полученными выше соотношениями, слагаемое дис-

сипативного типа в уравнении энергии будет иметь вид

210 Приложение. Построение КГД уравнений для плоского одномерного течения

∂

∂x

∂

∂x

(E +

p) +

2ρ

). (9.10.16)

Объединяя формулы (9.10.2), (9.10.13) и (9.10.16), получим последнее

уравнение КГД системы в виде

∂

∂t

E +

∂

∂x

u(E + p) =

∂

∂x

∂

∂x

(E +

p) +

(

∂

∂x

∂p

∂x

∂

∂x

τp

∂

∂x

(9.10.17)