Лекции - Математические модели и численные методы в динамике жидкости и газа

Подождите немного. Документ загружается.

8.3. Построение моментных уравнений 161

Таким образом, получаем уравнение для плотности:

∂

∂t

ρ + ∇

ρu

= ∇

τ∇

(ρu

+ g

В дальнейшем будем использовать (8.3.3)–(8.3.6), опуская соответ-

ствующие ссылки. Для получения уравнения импульса проинтегрируем

(8.3.9) с весом ξ

∂f

∂t

ξd~ω =

∂

∂t

ρu

∇

ξd~ω = ∇

(ρu

+ g

∇

τ∇

ξd~ω = (ρu

+ p

+ u

)).

Поскольку ξ

является сумматорным инвариантом, то и в этом случае

Iξ

ξd~ω = 0.

Комбинируя полученые выражения, получаем уравнение для ρu

∂

∂t

ρu

+ ∇

(ρu

+ g

) = ∇

τ∇

(ρu

+ p

+ u

)).

С целью получить уравнение для поступательной энергии E

осред-

ним (8.3.9) с весом

/2:

∂f

∂t

ξd~ω =

∂

∂t

∇

ξd~ω = ∇

+ c

d~c = ∇

+ p

∇

τ∇

ξd~ω = ∇

τ∇

+2u

Для интеграла столкновений I величина

/2 уже не является сумма-

торным инвариантом, поскольку возможен обмен энергией между посту-

пательными и вращательными степенями свободы, и последний интеграл

не обращается в нуль. Назовем его обменным членом и обозначим:

ξd~ω = S

162 Глава 8. КГДР уравнения для описания течений неравновесного газа

Комбинируя полученные выражения и дифференцируя по частям по-

следнее слагаемое, в которое входит квадрат давления, получим:

∂

∂t

+ ∇

+ p

) = ∇

τ∇

+ 2 u

) +

∇

τp

∇

+ S

Чтобы получить уравнение для вращательной энергии E

, необходимо

осреднить (8.3.9) с весом ε

в случае 2R молекул, и с весом ε

в случае

3R молекул; эти величины определяются в (8.3.4)–(8.3.5).

Для первого варианта осреднения получим:

∂f

∂t

ξd~ω =

∂

∂t

∇

ξd~ω = ∇

d~c

d~ω = ∇

∇

τ∇

ξd~ω = ∇

τ∇

(ρu

)

= ∇

τ∇

Обменный член обозначим как

Iε

ξd~ω = S

Комбинируя вместе полученные выражения и дифференцируя по частям

слагаемое, содержащее произведение давлений, получим уравнение для

вращательной энергии 2R молекул:

∂

∂t

+ ∇

= ∇

τ∇

+ ∇

∇

+ ∇

τp

∇

+ S

Аналогично вычислим для 3R случая, при этом правая часть изме-

нится:

∂

∂t

+ ∇

= ∇

τ∇

∇

τp

∇

+ S

Изложенный здесь способ получения моментных уравнений приводит

к выражениям для теплового потока с числом Прандтля, равным едини-

це. Для обобщения уравнений на случай произвольного числа Прандтля

предпоследние слагаемые в уравнениях для поступательной и враща-

тельной энергий следует домножить на величину P r

−1

. Для определения

числа Прандтля можно воспользоваться аппроксимацией Эйкена [70]:

P r =

4γ

9γ − 5

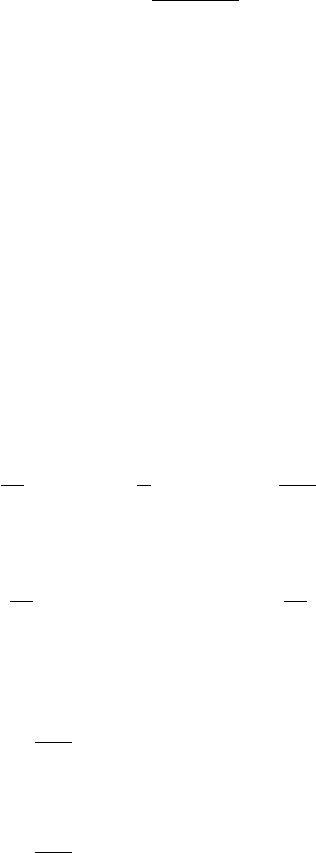
8.4. Вычисление обменных членов 163

где γ определяется в (8.3.8); в случае 2R газа γ = 7/5, P r = 14/19, в

случае 3R газа γ = 8/6, P r = 16/21.

8.4 Вычисление обменных членов

Обменные члены в правых частях полученных уравнений для энергий

представляют собой моменты интеграла столкновений уравнения Больц-

мана (8.3.1). Для их вычисления воспользуемся релаксационной моделью

интеграла столкновений в ее традиционном виде

I =

− f

где f

представляет собой функцию распределения f

для равновесного

случая, то есть для случая, когда T

= T

, соответственно p

= p

; τ

— среднее время вращательной релаксации, которое обычно

в несколько раз превышает максвелловское время релаксации τ.

= Zτ

1/Z - относительная частота неупругих соударений, τ

= τ/Ω - харак-

терное время между упругими соударениями, Ω = 30/((7 −2ω)(5 −2ω))

[12], [64].

Подставляя выражение для интеграла столкновений в определение

обменного члена, имеем для случая 2R:

− f)

ξd~ω =

2τ

− p

Для второго обменного члена:

− f)ε

ξd~ω =

− p

Подставляя выражения для среднего давления (8.3.7), получим для 2R

случая

5τ

− p

), S

= −S

Рассуждая аналогично, получим для 3R случая:

4τ

− p

), S

= −S

Заметим, что в соответствии с законом сохранения энергии:

+ S

= 0.

164 Глава 8. КГДР уравнения для описания течений неравновесного газа

8.5 КГДР уравнения для газа с двумя и тремя вра-

щательными степенями свободы

Получим окончательный вид КГДР уравнений для двухатомных (2R) и

полиатомных (3R) молекул в инвариантном относительно системы коор-

динат виде:

∂

∂t

ρ + ∇

ρu

= ∇

τ(∇

ρu

+ ∇

), (8.5.1)

∂

∂t

ρu

+ ∇

ρu

+ ∇

∇

τ∇

ρu

+ ∇

τ(∇

+ ∇

) + ∇

τ∇

, (8.5.2)

∂

∂t

+ ∇

+ p

) = ∇

τ(∇

+ 2 p

∇

) +

∇

+ P r

−1

∇

τp

∇

+ S

. (8.5.3)

Уравнение для вращательной энергии и обменные члены в случае 2R:

∂

∂t

+ ∇

= ∇

τ∇

+ ∇

∇

+ P r

−1

∇

τp

∇

+ S

. (8.5.4)

5τ

− p

); S

= −S

; E

ρ~u

; E

= p

γ = 7/5; P r = 14/19; p

= ρ

; p

= ρ

Уравнение для вращательной энергии и обменные члены в случае 3R:

∂

∂t

+ ∇

= ∇

τ∇

∇

+ P r

−1

∇

τp

∇

+ S

8.5. КГДР уравнения для газа с двумя и тремя вращательными степенями свободы165

4τ

− p

); S

= −S

; E

ρ~u

; E

γ = 8/6; P r = 16/21; p

= ρ

; p

= ρ

Уравнение для вращательной энергии E

может быть приближено

следующим образом:

∂

∂t

+ u

∇

= (T

− T

)/τ

Такая форма записи часто используется в работах по исследованию ре-

лаксационных процессов (см. [12], с. 117).

Для пространственно-одномерных течений эти уравнения упрощают-

ся:

∂ρ

∂t

∂

∂r

ρu =

∂

∂r

∂

∂r

ρu

∂

∂r

τr

∂

∂r

∂ρu

∂t

∂

∂r

ρu

∂

∂r

∂

∂r

∂

∂r

ρu

∂

∂r

τr

∂

∂r

u − 2ν

u +

∂

∂r

∂

∂r

∂E

∂t

∂

∂r

u(E

+ p

) =

∂

∂r

∂

∂r

+ 2 p

∂

∂r

τr

∂

∂r

∂

∂r

∂

∂r

+ P r

−1

∂

∂r

τp

∂

∂r

+ S

Для случая 2R:

∂E

∂t

∂

∂r

∂

∂r

∂

∂r

∂

∂r

∂

∂r

+ P r

−1

∂

∂r

τp

∂

∂r

+ S

Для случая 3R:

∂E

∂t

∂

∂r

∂

∂r

∂

∂r

∂

∂r

∂

∂r

+ P r

−1

∂

∂r

τp

∂

∂r

+ S

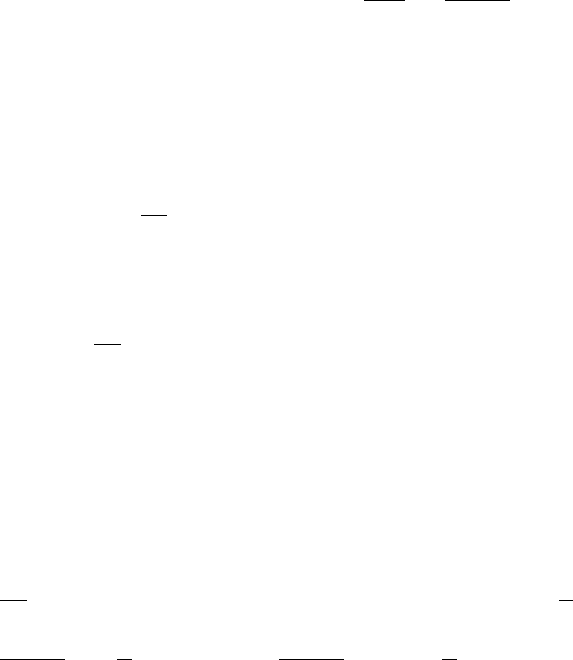
166 Глава 8. КГДР уравнения для описания течений неравновесного газа

Здесь ν = 0 соответствует плоскому случаю, ν = 1 — цилиндрической

симметрии, ν = 2 — сферической.

Дополненные граничными условиями, выписанные здесь системы

уравнений представляют собой замкнутую модель для расчета течений

умеренно-разреженного газа с возможной неравновесностью между по-

ступательными и вращательными степенями свободы.

В случае теплового равновесия газа по поступательным и враща-

тельным степеням свободы, то есть в случае, когда T

= T

= T и

= p

= p, полная энергия единицы объема равна

E = E

+ E

ρ~u

γ − 1

где γ определяется в соответствии с (8.3.8).

При этом вид уравнений для плотности и импульса не изменится:

∂

∂t

ρ + ∇

ρu

= ∇

τ(∇

ρu

+ ∇

p),

∂

∂t

ρu

+ ∇

ρu

+ ∇

p = ∇

τ∇

ρu

∇

τ(∇

+ ∇

) + ∇

τ∇

Сложим уравнения для E

и E

и получим уравнение для полной

энергии E:

∂

∂t

E + ∇

(E + p) = ∇

τ(∇

(E + 2p)u

∇

p) +

γ − 1

∇

p + P r

−1

γ − 1

∇

τp∇

Заметим, что приведенное выше уравнение энергии сразу может быть

получено при осреднении приближенного уравнения (8.3.9) с сумматор-

ным инвариантом

/2 + ε

и обобщении полученного уравнения на слу-

чай P r 6= 1.

Последняя система уравнений совпадает с выписанной ранее КГД си-

стемой. То есть, в равновесном случае КГДР система переходит в систему

КГД с соответствующими значениями γ и P r.

8.6. Результаты численного моделирования 167

8.6 Результаты численного моделирования

На основе полученных КГДР уравнений решалась задача о течении азо-

та, который рассматривался как 2R газ с параметрами Z = 5, ω = 0.75,

где ω — показатель степени в законе зависимости вязкости от температу-

ры. Полученные результаты сопоставлялись с расчетами, выполненными

в рамках DSMC подхода. Рассматривались одномерные задачи о релак-

сации поступательной и вращательной температуры в потоке, и задача

численного моделирования структуры ударной волны. Численный алго-

ритм представлял собой явную по времени разностную схему второго

порядка точности без искусственных регуляризаторов, которая анало-

гична описанной в Главе 5.

8.6.1 Задача о релаксации.

Рассмотрим стационарное одномерное течение газа (Ma = 3.571) с

неравновесностью во входном сечении при x = 0, которое характери-

зуется температурами T

T 1

6= T

, плотностью ρ

и скоростью u

. Враща-

тельная и поступательная температуры эволюционируют к равновесно-

му состоянию с ростом x.

Пусть значения ρ, u, T

и T

приведены к безразмерному виду на

основе соответствующих значений в сечении x = 0, которые обозначе-

ны индексами (1). Эти величины выбраны равными соответствующим

значениям для DSMC вычислений. T

(x = 0) = T

. Координата x нор-

мирована на среднюю длину свободного пробега λ

, где

η(T

)

2(R/M)T

2(7 − ω)(5 − ω)

√

В расчетах по методу DSMC использована модель соударений, кото-

рая приблизительно соответствует значению Z = 5. Наличие градиента

температуры на входной границе расчетной области вызывает трудности

при постановке граничных условий для DSMC вычислений. Условия на

левой входной границе в этом алгоритме реализованы следующим обра-

зом: молекулы с равновесными температурами T

и T

впрыскиваются

в область расчета из зоны, расположенной в точке x < 0. Значения га-

зодинамических параметров, полученные в DSMC вычислениях в точке

x = 0, задаются в качестве граничных условий для КГДР вычислений.

На правой выходной границе для КГДР уравнений ставятся условия сно-

168 Глава 8. КГДР уравнения для описания течений неравновесного газа

са потока, или "мягкие граничные условия". Кинетический аналог этих

же условий ставится и в DSMC алгоритме. Шаг пространственной сетки

выбирался равным h = 1 и 0.5.

Результаты, полученные по обоим методам, оказываются близкими,

что характеризует точность построенной КГДР модели (рис. 8.1).

0 10 20 30 40 50 60 70 80

0.70

0.80

0.90

1.00

1.10

1.20

Tav

0 10 20 30 40 50 60 70 80

0.980

0.990

1.000

1.010

1.020

Рис. 8.1: Профили температуры, плотности и скорости в задаче о релаксации. Сплош-

ная линия соответствует методу DSMC, пунктирная — модели КГДР

8.6.2 Задача о структуре неподвижной ударной волны.

Задача о структуре ударной волны решалась в следующих вариантах:

число Маха набегающего потока Ma = 1.71 (Z = 5 и Z = 10), что

соответствует DSMC вычислениям, приведенным в [12] стр.298, и для

чисел Маха Ma = 7 и 12.9, что соответствует DSMC расчетам [79].

Полученные в расчетах профили плотности, скорости и температур

представлены на рис. 8.2–8.3, где значения координаты x нормировано на

среднюю длину свободного пробега в набегающем потоке. Ординаты нор-

мированы обычным образом с использованием соотношений Рэнкина–

Гюгонио между параметрами перед ударной волной (1) и за ней (2), т. е.

= (ρ −ρ

(1)

)/(ρ

(2)

−ρ

(1)

), где f

— значение плотности на рисунке, ρ

(1)

(2)

— значения на границах; аналогично для температуры. Для скорости

= (u − u

(2)

)/(u

(1)

− u

(2)

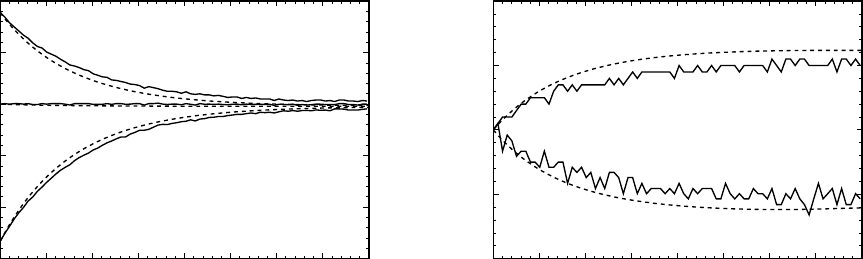
На рис. 8.2 (Z = 5) видны характерные особенности профилей в дан-

ной задаче. А именно, взаимное расположение профилей соответствует

результатам Берда, где профиль поступательной температуры T

имеет

небольшой максимум (T

= 1.021), причем этот профиль расположен

левее профиля вращательной температуры T

, который максимума не

8.6. Результаты численного моделирования 169

-10 -5 0 5 10

0.0

0.2

0.4

0.6

0.8

1.0

-10 -5 0 5 10 15

0.0

0.2

0.4

0.6

0.8

1.0

Рис. 8.2: Задача об ударной волне, Ma = 1.71, Z = 5 (слева) и Z = 10 (справа).

Сплошная линия соответствует ρ, пунктирная T

, точками обозначена T

, длинным

пунктиром T

и штрихпунктиром u

-10 -5 0 5 10

0.0

0.2

0.4

0.6

0.8

1.0

-10 -5 0 5 10

0.0

0.2

0.4

0.6

0.8

1.0

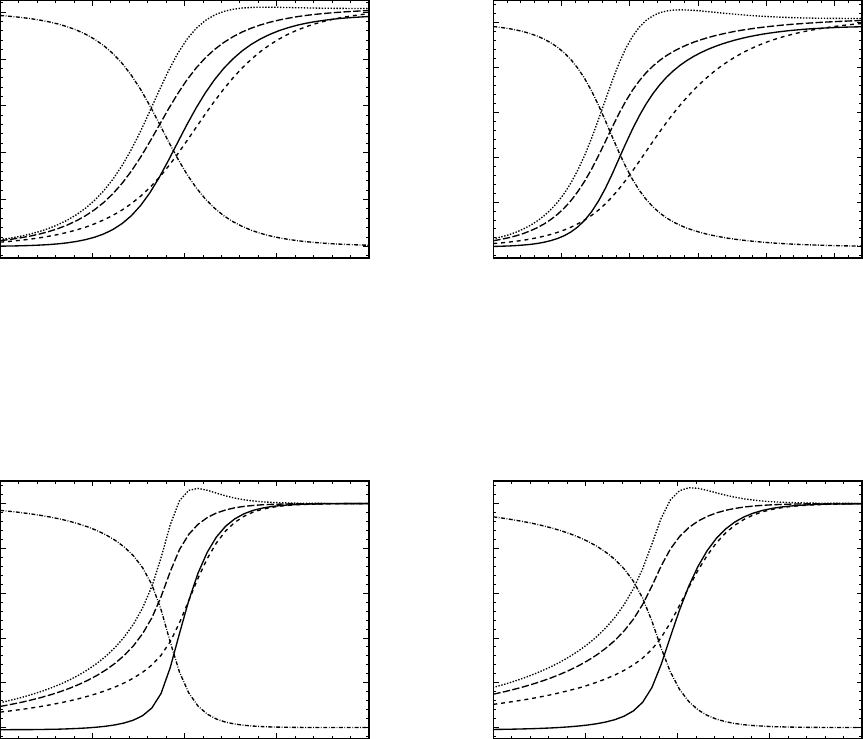
Рис. 8.3: Задача об ударной волне; Ma = 7.0, Z = 5 (слева); Ma = 12.9, Z = 5

(справа); обозначения те же, что на рис. 8.2

имеет. Обратная толщина профиля плотности ударной волны составля-

ет λ

/δ = 0.152. С увеличением Z толщина ударной волны возрастает

( λ

/δ = 0.136), а превышение величины поступательной температуры

над ее значением за фронтом увеличивается примерно в два раза

= 1.058), как это и было показано в [12].

Результаты расчетов для Ma = 7.0 и Ma = 12.9 представлены на рис.

8.3. Они очень близки к результатам [79]. В частности, в обоих случаях

профили ρ и T

расположены очень близко. Кроме того значения мак-

симумов T

также находятся в хорошем соответствии с расчетами [79],

где T

= 1.068 для Ma = 7.0, и T

= 1.070 для Ma = 12.9. Обрат-

ная толщина ударной волны λ

/δ для этих случаев составляет 0.297 и

170 Глава 8. КГДР уравнения для описания течений неравновесного газа

0.244 соответственно. Однако в области перед ударной волной значение

обоих температур T

и T

, рассчитанных по КГДР модели, оказываются

завышенными по сравнению с данными DSMC.

Полученное соответствие численных результатов данным расчетов

по кинетическому DSMC алгоритму указывает на хорошую точность

предложенной КГДР модели для описания поступательно-вращательной

неравновесности в газе.

Использование КГДР моделей для расчета осесимметричных струй-

ных течений и сопоставление полученных результатов с данными экс-

периментов изложено в [22] и [23]. Здесь показаны преимущества учета

поступательно-вращательной неравновесности при численном моделиро-

вании недорасширенных струй CO

и N