Лекции - Математические модели и численные методы в динамике жидкости и газа
Подождите немного. Документ загружается.

6.3. Аппроксимация частных производных и разностная схема 111
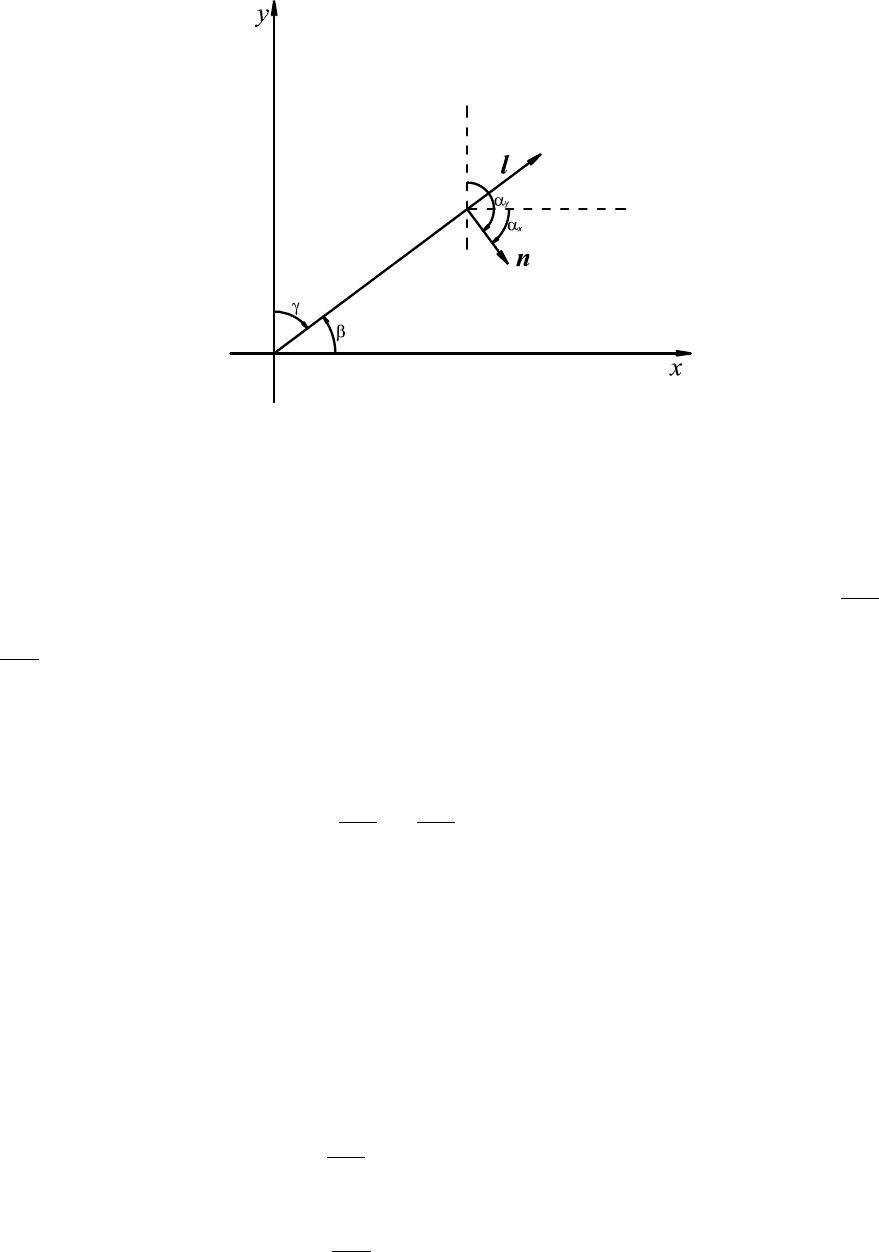
Рис. 6.2: Связь углов между касательной и нормалью
Пользуясь этими двумя формулами, найдем частные производные
∂P
∂x
и
∂Q
∂y
. Для этого рассмотрим дивергенцию вектора
~
A = {P , Q}. Используя
формулы (6.3.1)–(6.3.5), получим
ZZ
G
µ
∂P
∂x
+
∂Q
∂y
¶
dxdy =
Z
∂G
−Q dx + P dy =
=
Z
∂G
(−Q cos β + P cos γ) dl =
Z
∂G
(Qn
y
+ P n
x
) dl =
Z
∂G
(
~
A ·~n) dl.(6.3.6)
Далее
ZZ
G
∂P
∂x
dxdy =
Z
∂G
P n
x
dl, (6.3.7)
ZZ
G
∂Q
∂y
dxdy =
Z
∂G
Qn
y
dl, (6.3.8)
112 Глава 6. Алгоритмы решения КГД уравнений на неструктурированных сетках
или, используя формулу о среднем, получим
∂P
∂x
=
1
S
Z
∂G
P n
x
dl (6.3.9)
∂Q
∂y
=
1
S
Z
∂G
Qn
y
dl, (6.3.10)
где S — площадь области G.
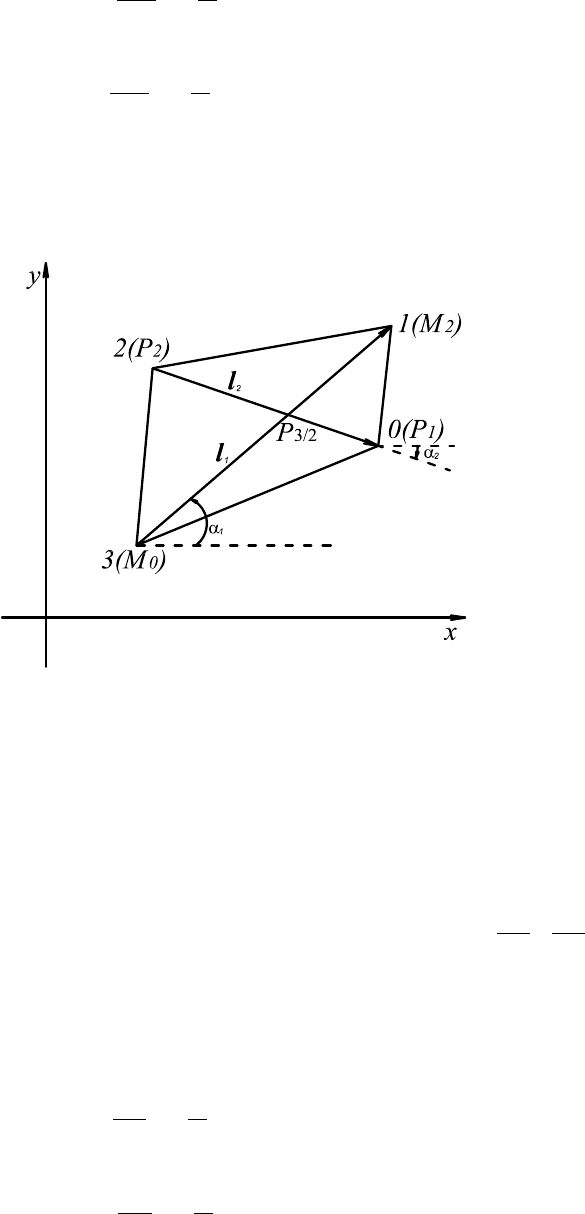
Рис. 6.3: Контур ∂G для вычисления частных производных
Рассмотрим способы для выражения производных. Обратимся к рис. 6.3
и рассмотрим, например, четырехугольник M
0
, P
1
, M
2
, P
2
, который об-
разует область G. Рассмотрим величину f, определенную в вершинах
четырехугольника, и найдем ее частные производные
∂f
∂x
,
∂f
∂y
в точке
P
3/2
.
Частные производные можно искать двумя способами: используя фор-
мулы Грина (6.3.9)–(6.3.10), т.е через интеграл по контуру 0123:
∂f
∂x
=
1
S
Z
∂G
fn
x
dl, (6.3.11)
∂f
∂y
=
1
S
Z
∂G
fn
y
dl, (6.3.12)
6.3. Аппроксимация частных производных и разностная схема 113
или используя производные по направлениям l
1
, l
2
:
∂f
∂l
1
=
∂f
∂x
∂x
∂l
1
+
∂f
∂y
∂y
∂l
1
, (6.3.13)
∂f
∂l
2
=
∂f
∂x
∂x
∂l
2
+
∂f
∂y
∂y
∂l
2
. (6.3.14)
Раскроем интегралы в формулах (6.3.11)–(6.3.12) по аналогии с (6.2.4).
Компоненты единичного вектора нормали можно выразить через коор-
динаты точек следующим образом
~n(x1, y1, x2, y2) = {cos α , sin α} =
= {y
2
− y
1
, x
1
− x
2
} ·
1
p
(x
2
− x
1
)
2
+ ( y
2
− y
1
)
2
, (6.3.15)
а площадь
S =
1
2
[(x
3
− x
1
)(y
0
− y
2
) + (x
0
− x
2
)(y
1
− y
3
)] . (6.3.16)
Далее:
S
∂f
∂x
=
R
0123
fn
x
dl =
3
P
i=0
f
i+1
+ f
i
2
(y
i+1
− y
i
) =
=
f
1
+ f
0
2
(y
1
− y
0
) +
f
2
+ f
1
2
(y
2
− y
1
)+
+
f
3
+ f
2
2
(y
3
− y
2
) +
f
0
+ f
3
2
(y
0
− y
3
) =
=
1
2
[y
1
(f
0
− f
2
) + y
0
(f
3
− f
1
) + y
2
(f
1
− f
3
) + y
3
(f
2
− f
0
)] =
=
1
2
[(f
2
− f
0
)(y
3
− y
1
) + (f
1
− f
3
)(y
2
− y
0
)].
Итак, в результате получим формулу, выражающую производную в P
3/2
через координаты узлов контура 0123 и значения функции в этих узлах
∂f
∂x
=
(f
2
− f
0
)(y
3
− y
1
) + (f
1
− f
3
)(y
2
− y
0
)
2S
. (6.3.17)
Аналогично
∂f
∂y
=
(f
2
− f
0
)(x
1
− x
3
) + (f
1
− f
3
)(x
0
− x
2
)
2S
. (6.3.18)
114 Глава 6. Алгоритмы решения КГД уравнений на неструктурированных сетках
Теперь рассмотрим второй способ, т.е. выразим частные производные
через производные по направлению. Для этого решим систему (6.3.13)–
(6.3.14) относительно
∂f
∂x
,
∂f
∂y
:
∂f
∂l
1
=
∂f
∂x
∂x
∂l
1
+
∂f
∂y
∂y
∂l
1
∂f
∂l
2
=
∂f
∂x
∂x
∂l
2
+
∂f
∂y
∂y
∂l
2
,
или
∂f
∂l
1
=
∂f
∂x
cos α
1
+
∂f
∂y
sin α
1
∂f
∂l
2
=
∂f
∂x
cos α
2
+
∂f
∂y
sin α
2
,
откуда
∂f
∂x
=
∂f
∂l
1
sin α
2
−
∂f
∂l
2
sin α
1
sin α
2
cos α
1
− sin α
1
cos α
2
, (6.3.19)
∂f
∂y
=
∂f
∂l
1
cos α
2
−
∂f
∂l
2
cos α
1
sin α
1
cos α
2
− sin α
2
cos α
1
. (6.3.20)
Используя формулы (6.3.3)–(6.3.5), получим
∂f
∂x
= −
∂f
∂l
1
sin α
2
−
∂f
∂l
2
sin α
1
sin α
2
cos α
1
− sin α
1
cos α
2
, (6.3.21)
∂f
∂y
=
∂f
∂l
1
cos α
2
−
∂f
∂l
2
cos α
1
sin α
1
cos α
2
− sin α
2
cos α
1
. (6.3.22)
или
∂f
∂x
=
∂f
∂l
1
n
2x
−
∂f
∂l
2
n
1x
−n
2x
n
1y
+ n
1x
n
2y
, (6.3.23)
∂f
∂y
= −
∂f
∂l
1
n
2y
+
∂f
∂l
2
n
1y
−n
1x
n
2y
+ n
2x
n
1y
. (6.3.24)

6.3. Аппроксимация частных производных и разностная схема 115
Применяя (6.3.15), имеем
∂f
∂x
=
f
1
− f
3
L
13
y
0
− y
2
L
20
−
f
0
− f
2
L
20
y
1
− y
3
L
13
−
y
0
− y
2
L
20
x
3
− x
1
L
13
+
y
1
− y
3
L
13
x
2
− x
0
L
20
=
=
−(f
1
− f
3
)(y
2
− y
0
) + (f
2
− f
0
)(y
1
− y
3
)
−(y
2
− y
0
)(x
1
− x
3
) + (y
1
− y
3
)(x
2
− x
0
)
=
=
(f
2
− f
0
)(y
1
− y
3
) − (f
1
− f
3
)(y
2
− y
0
)
−2S
,
что совпадает с (6.3.17). Аналогично для
∂f
∂y
.
Далее, выразив компоненты вектора
~
W через ρ, ~u, p,
∂ρ
∂x
,
∂ρ
∂y
,
∂~u
∂x
,
∂~u
∂y
,
∂p
∂x
,
∂p
∂y
и частные производные, можем решить систему (6.2.5) относи-
тельно ρ, ~u, p.
Таким образом, разностная схема примет следующий вид:
ˆρ
i
= ρ
i
−
∆t
S
X
k
³
j
x
m,k+1/2
n
x
k+1/2
+ j
y
m,k+1/2
n
y
k+1/2
´
L
k
,
ˆ
u
x
i
=
1
ˆρ
i
Ã
ρ
i
u
x
i
−
∆t
S
X
k
³h
Π
xx
k+1/2
− j
x
m,k+1/2
u
x
k+1/2
− p
i
n
x
k+1/2
+
+
h
Π
xy
k+1/2
− j
x
m,k+1/2
u
y
k+1/2
i
n
y
k+1/2
´
L
k
´
,
ˆ
u
y
i
=
1
ˆρ
i
Ã
ρ
i
u
y
i
−
∆t
S
X
k
³h
Π
yx
k+1/2
− j
y
m,k+1/2
u
x
k+1/2
i
n
x
k+1/2
+
+
h
Π
yy
k+1/2
− j
y
m,k+1/2
u
y
k+1/2
− p
i
n
y
k+1/2
´
L
k
´
,
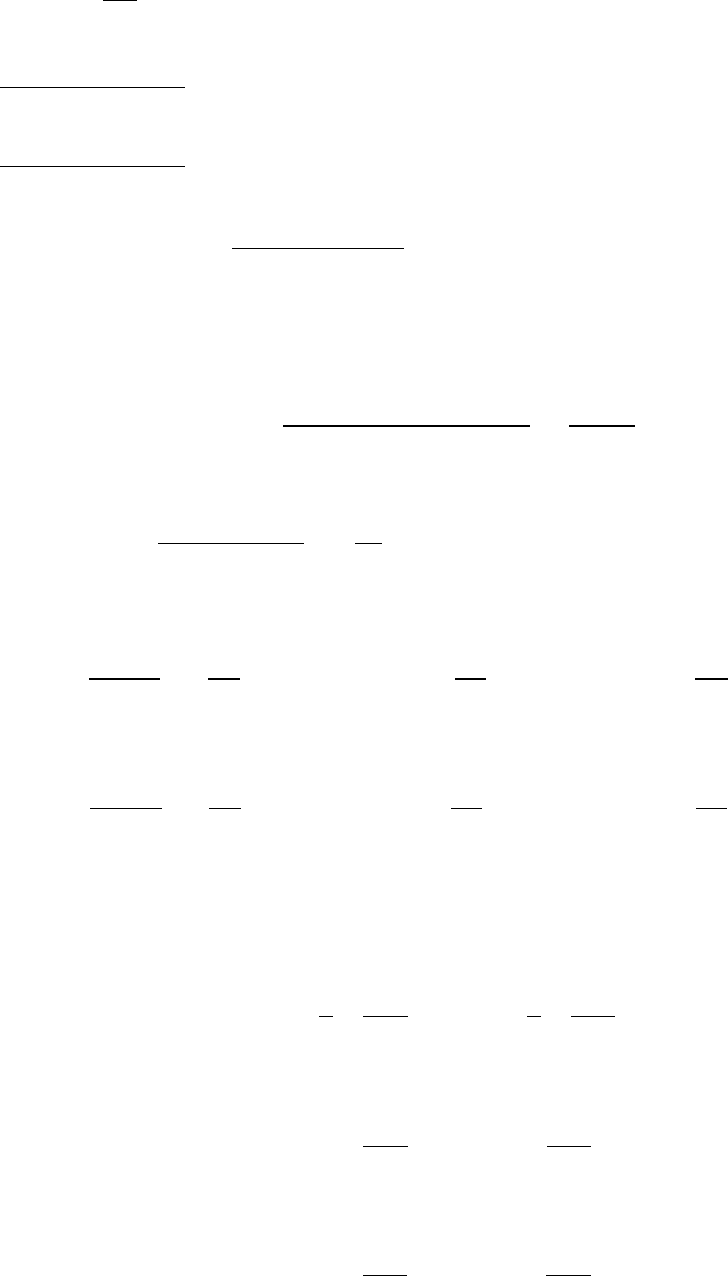
116 Глава 6. Алгоритмы решения КГД уравнений на неструктурированных сетках
ˆ
E
i
= E
i
+
∆t
S
X
k
³h
Π
xx
k+1/2
u
x
k+1/2
+ Π
xy
k+1/2
u
y
k+1/2
− q
x
k+1/2
−
−
E
k+1/2
+ p
k+1/2
ρ
k+1/2
j
x
m,k+1/2
¸
n
x
k+1/2
+
h
Π
yx
k+1/2
u
x
k+1/2
+ Π
yy
k+1/2
u
y
k+1/2
− q
y
k+1/2
−
−
E
k+1/2
+ p
k+1/2
ρ
k+1/2
j
y
m,k+1/2
¸
n
y
k+1/2
¶
L
k
,
ˆp
i
= (γ − 1)
µ
ˆ
E
i
− ˆρ
i
(
ˆ
u
x
i
)
2
+ (
ˆ
u
y
i
)
2
2
¶
.
Здесь индекс i — номер узла сетки, k — номер узла контура L.
E
k+1/2
= ρ
k+1/2
(u
x
k+1/2
)
2
+ ( u
y
k+1/2
)
2
2
+
1
γ − 1
p
k+1/2
,
τ
k
= α
P
K
k=0
L
k,k+1
K
µ
γ
p
k
ρ
k
¶
−1/2
, η
k
= p
k
Sc τ
k
,
w
x
k+1/2
=
τ
k+1/2
ρ
k+1/2
"
µ
∂
∂x
ρ(u
x
)
2
¶
k+1/2
+
µ
∂
∂y
ρu
x
u
y
¶
k+1/2
+
µ
∂p
∂x
¶
k+1/2
#
,
w
y
k+1/2
=
τ
k+1/2
ρ
k+1/2
"
µ
∂
∂x
ρu
x
u
y
¶
k+1/2
+
µ
∂
∂y
ρ(u
y
)
2
¶
k+1/2
+
µ
∂p
∂y
¶
k+1/2
#
,
~
j
m,k
= ρ(~u
k
− ~w
k
),
Π
xx
ns
k+1/2
= η
k+1/2
"
4
3
µ
∂u
x
∂x
¶
k+1/2
−
2
3
µ
∂u
y
∂y
¶
k+1/2
#
,
Π
xy
ns
k+1/2
= η
k+1/2
"
µ
∂u
x
∂x
¶
k+1/2
+
µ
∂u
y
∂x
¶
k+1/2
#
,
Π
yx
ns
k+1/2
= η
k+1/2
"
µ
∂u
y
∂x
¶
k+1/2
+
µ
∂u
x
∂y
¶
k+1/2
#
,
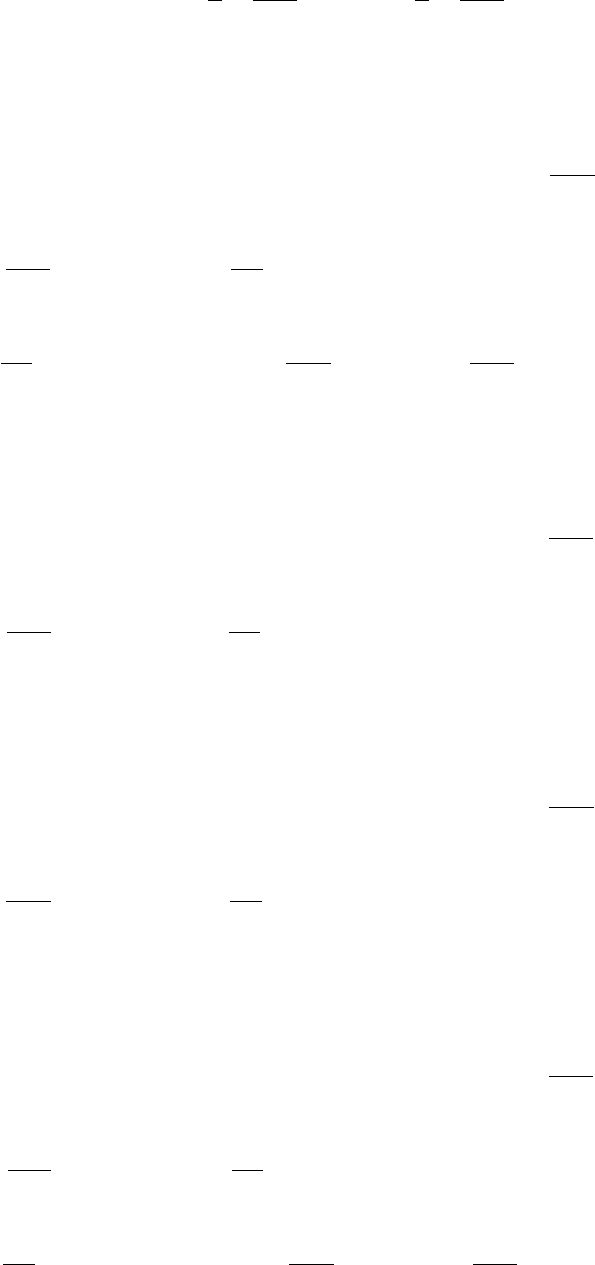
6.3. Аппроксимация частных производных и разностная схема 117
Π
yy
ns
k+1/2
=
η
k+1/2
"
4
3
µ
∂u
y
∂y
¶
k+1/2
−
2
3
µ
∂u
x
∂x
¶
k+1/2
#
,
Π
xx
k+1/2
= Π
xx
ns
k+1/2
+ τ
k+1/2
(
u
x
k+1/2
"
ρ
k+1/2
Ã
u
x
k+1/2
µ
∂u
x
∂x
¶
k+1/2
+
+u
y
k+1/2
µ
∂u
x
∂y
¶
k+1/2
!
+ 2
µ
∂p
∂x
¶
k+1/2
#
+
+u
y
k+1/2
µ
∂p
∂y
¶
k+1/2
+ γp
k+1/2
Ã
µ
∂u
x
∂x
¶
k+1/2
+
µ
∂u
y
∂y
¶
k+1/2
!)
,
Π
xy
k+1/2
= Π
xy
ns
k+1/2
+ τ
k+1/2
(
u
x
k+1/2
"
ρ
k+1/2
Ã
u
x
k+1/2
µ
∂u
y
∂x
¶
k+1/2
+
+u
y
k+1/2
µ
∂u
y
∂y
¶
k+1/2
!#
+
µ
∂p
∂y
¶
k+1/2
)
,
Π
yx
k+1/2
= Π
yx
ns
k+1/2
+ τ
k+1/2
(
u
y
k+1/2
"
ρ
k+1/2
Ã
u
x
k+1/2
µ
∂u
x
∂x
¶
k+1/2
+
+u
y
k+1/2
µ
∂u
x
∂y
¶
k+1/2
!#
+
µ
∂p
∂x
¶
k+1/2
)
,
Π
yy
k+1/2
= Π
yy
ns
k+1/2
+ τ
k+1/2
(
u
y
k+1/2
"
ρ
k+1/2
Ã
u
x
k+1/2
µ
∂u
y
∂x
¶
k+1/2
+
+u
y
k+1/2
µ
∂u
y
∂y
¶
k+1/2
!
+ 2
µ
∂p
∂y
¶
k+1/2
#
+
+u
x
k+1/2
µ
∂p
∂x
¶
k+1/2
+ γp
k+1/2
Ã
µ
∂u
x
∂x
¶
k+1/2
+
µ
∂u
y
∂y
¶
k+1/2
!)
,

118 Глава 6. Алгоритмы решения КГД уравнений на неструктурированных сетках
q
x
k+1/2
= −
η
k+1/2
P r
γ
γ − 1
µ
∂
∂x
p
ρ
¶
k+1/2
−
−τ
k+1/2
ρ
k+1/2
u
x
k+1/2
"
1
γ − 1
Ã
u
x
k+1/2
µ
∂
∂x
p
ρ
¶
k+1/2
+ u
y
k+1/2
µ
∂
∂y
p
ρ
¶
k+1/2
!
+
+p
k+1/2
Ã
u
x
k+1/2
µ
∂
∂x
1
ρ
¶
k+1/2
+ u
y
k+1/2
µ
∂
∂y
1
ρ
¶
k+1/2
!#
,
q
y
k+1/2
= −
η
k+1/2
P r
γ
γ − 1
µ
∂
∂y
p
ρ
¶
k+1/2
−
−τ
k+1/2
ρ
k+1/2
u
y
k+1/2
"
1
γ − 1
Ã
u
x
k+1/2
µ
∂
∂x
p
ρ
¶
k+1/2
+ u
y
k+1/2
µ
∂
∂y
p
ρ
¶
k+1/2
!
+
+p
k+1/2
Ã
u
x
k+1/2
µ
∂
∂x
1
ρ
¶
k+1/2
+ u
y
k+1/2
µ
∂
∂y
1
ρ
¶
k+1/2
!#
.
Здесь K — число узлов в контуре L, P r — число Прандтля, Sc — число
Шмидта, γ — показатель адиабаты, α — регуляризатор (0 6 α 6 1).
Приведенная здесь разностная аппроксимация КГД уравнений по-
строена для плоских двумерных течений на основе записи этих урав-
нений в виде (5.1.1) – (5.1.4). Разностная аппроксимация уравнений в
цилиндрической геометрии строится аналогичным образом на основе за-
писи уравнений в виде (5.2.1) – (5.2.4).
6.4 Аппроксимация граничных условий
Для замыкания системы КГД уравнений и ее численного решения оста-
лось рассмотреть аппроксимацию граничных условий. Для этого обра-
тимся к рис. 6.4.
Рис. 6.4: Аппроксимация граничных условий.

6.4. Аппроксимация граничных условий 119
Здесь B
j
— граничные узлы, M
i
— внутренние узлы сетки. Рассмот-
рим аппроксимацию граничных условий для некоторой величины f в
узле B
j
. Для остальных граничных узлов аппроксимация производится
аналогичным образом. В результате расчета по разностной схеме (6.2.5)
были определены значения величины f во внутренних узлах сетки. Бу-
дем определять значения на границе через средневзвешенные значения
f во внутренних узлах, треугольники которых содержат данный гра-
ничный узел в качестве вершины. Для граничного узла B
j
это будут
внутренние узлы: M
1
, M
2
, ··· , M
n
.
Граничное условие I рода (условие Дирихле)
Запишем граничное условие Дирихле:
f|
Γ
= f
0
, (6.4.1)
где Γ — граница области.
Аппроксимацию запишем следующим образом:
f(B
j
) = f
0
(6.4.2)
Граничное условие II рода (условие Неймана)
Запишем граничное условие Неймана:
∂f
∂n
¯
¯
¯
¯
Γ
= f
0
. (6.4.3)
Аппроксимацию запишем следующим образом:
f(B
j
) =
1
N
i=N
X
i=1
f(M
i
) +
f
0
N
i=N
X
i=1
L(B
j
, M
i
). (6.4.4)
Здесь L(B
j
, M
i
) — расстояние между точками B
j
и M
i
.
Граничное условие III рода
Запишем граничное условие III рода:
·
∂f
∂n
+ βf
¸
¯
¯
¯
¯
Γ
= f
0
. (6.4.5)

120 Глава 6. Алгоритмы решения КГД уравнений на неструктурированных сетках
Аппроксимацию запишем следующим образом:
f(B
j
) =
i=N
X
i=1
f(M
i
) + f
0
i=N
X
i=1
L(B
j
, M
i
)
N + β
i=N
X
i=1
L(B
j
, M
i
)
. (6.4.6)
Здесь β — некоторая константа.
В заключение отметим, что приведенный выше подход естественным
образом обобщается на случай rz-геометрии.
