Лекции - Математические модели и численные методы в динамике жидкости и газа
Подождите немного. Документ загружается.

5.8. Задача о течении в окрестности цилиндра 91
5.8 Задача о течении в окрестности цилиндра
5.8.1 Постановка задачи и особенности численного алгоритма
В качестве примера реализации выписанного двумерного алгоритма при-
ведем результаты расчета задачи о течении в окрестности цилиндриче-
ского торца радиуса R
c
, который помещен в однородный сверхзвуковой
поток вязкого сжимаемого теплопроводного газа под нулевым углом ата-
ки.
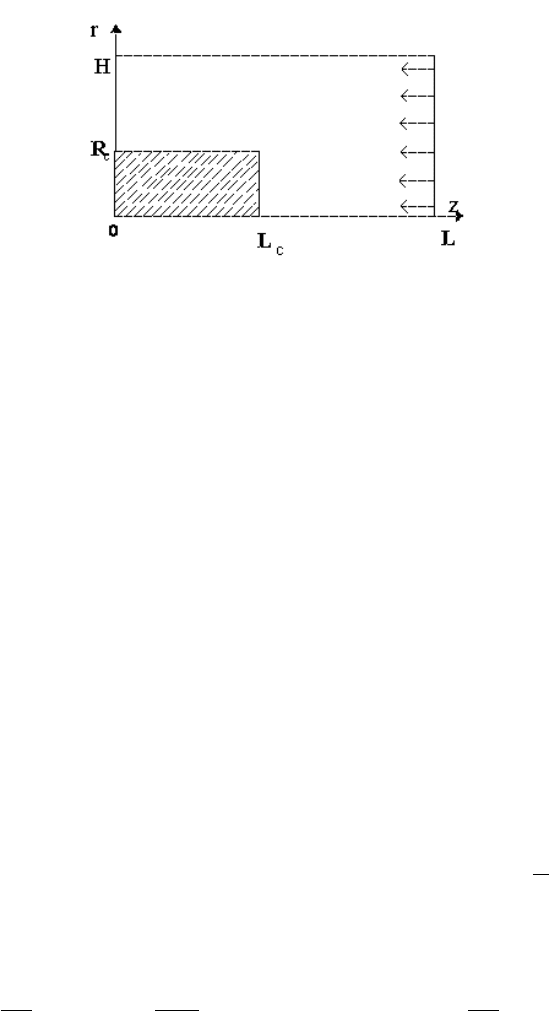
Рис. 5.5: Обтекание цилиндрического торца
Введем цилиндрическую систему координат, направив ось z вдоль оси
цилиндра, а ось r вдоль поверхности торца (рис. 5.5). Размеры области
расчета L × H, размеры цилиндра L
c
× R
c
, где R
c
— радиус цилиндра.
Рассматриваем течение одноатомного газа твердых сфер со следую-
щими параметрами: γ = 5 /3, P r = 2/3, Re = 1000, Sc = 0.77, ω = 0.5.
В качестве начальных условий для системы (5.2.1)–(5.2.4) используем
параметры набегающего потока:
ρ|
t=0
= ρ
∞
, u
z
|
t=0
= −U
∞
, u
r
|
t=0
= 0, p|
t=0
= p
∞
. (5.8.1)
После введения безразмерных величин, эти параметры равны ρ
∞
= 1,
U
∞
= −Ma и p
∞
= 1/γ.
На правой входной границе (z = L, 0 < r < H) задаются параметры
набегающего потока (5.8.1):
ρ = 1, u
z
= −Ma, u
r
= 0, p =
1
γ
, (5.8.2)
на оси симметрии (L
c
< z < L, r = 0) — "условия симметрии":
∂ρ
∂r
= 0,
∂u
z
∂r
= 0, u
r
= 0,
∂p
∂r
= 0, (5.8.3)

92Глава 5. Численные алгоритмы решения нестационарных задач газовой динамики
на торце цилиндра (z = L
c
, 0 < r < R
c
) — "условия скольжения" для
скорости:
∂ρ
∂z
= 0, u
z
= 0,
∂u
r
∂z
= 0,
∂p
∂z
= 0, (5.8.4)
на боковой поверхности цилиндра (0 < z < L
c
, r = R
c
) — "условия
прилипания" для скорости:
∂ρ
∂r
= 0, u
z
= 0, u
r
= 0,
∂p
∂r
= 0. (5.8.5)
Поверхность цилиндра предполагается адиабатической.
На левой выходной и верхней свободной границах ставятся так назы-
ваемые "мягкие" граничные условия, то есть предполагается равенство
нулю нормальных производных плотности, давления и компонент скоро-
сти.
Выходная граница (z = 0, R
c
< r < H):
∂ρ
∂z
= 0,
∂u
z
∂z
= 0,
∂u
r
∂z
= 0,
∂p
∂z
= 0, (5.8.6)
свободная граница (0 < z < L, r = H):
∂ρ
∂r
= 0,
∂u
z
∂r
= 0,
∂u
r
∂r
= 0,
∂p
∂r
= 0. (5.8.7)
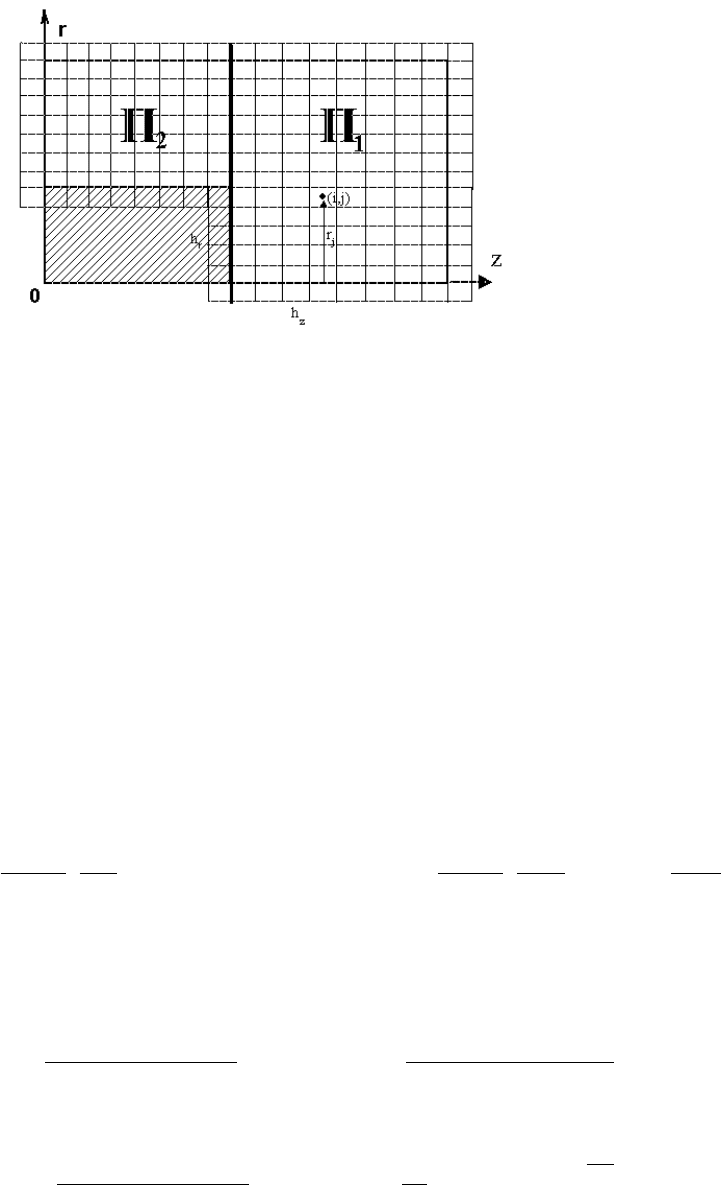
Расчетная область для этой задачи приведена на рис. 5.6. Для того,
чтобы с помощью введения фиктивных ячеек аккуратно аппроксимиро-
вать угловую точку с координатами L
c
, R
c
, модифицируем численный
алгоритм следующим образом. Разобьем расчетную область L × H на
две подобласти Π
1
и Π
2
:
Π
1
= {(z, r) : L
c
< z < L, 0 < r < R},
Π
2
= {(z, r) : 0 < z < L
c
, R
c
< r < H},
и будем искать численное решение в области G = Π
1
∪ Π
2
.
Алгоритм нахождения основных газодинамических величин ρ, u
z
, u
r
,
p на каждом временном слое включает два этапа. На первом этапе мы
заполняем все фиктивные ячейки, используя граничные условия. На вто-
ром этапе вычисляем параметры течения на следующем временном слое
bρ,bu
z
, bu
r
, bp во всех внутренних точках области по одним и тем же форму-
лам. Система уравнений на каждом временном шаге решается поочеред-
но: сначала в правой области Π
1
, а затем в левой области Π
2
(для данной
задачи, когда поток втекает справа). После этого происходит переход на
следующий шаг по времени.
5.8. Задача о течении в окрестности цилиндра 93
Рис. 5.6: Расчетная область и структура сетки
5.8.2 Результаты расчета
В данной задаче число Рейнольдса выбрано достаточно большим, и на
торце цилиндра поставлены условия скольжения для скорости. Поэтому
точность приведенных далее расчетов можно оценивать путем сопостав-
ления параметров газа на торце цилиндра с параметрами торможения.
Параметры торможения — это значения плотности ρ
s
, давления p
s
и температуры T
s
в точке торможения, вычисленные с использованием
теоремы Бернулли (см, например, [3]):
p
s
= p
2
µ
1 +
γ − 1
2
u
2
z2
c
2
2
¶
γ/(γ−1)
, T
s
= T
2
µ
1 +
γ − 1
2
u
z2
2
c
2
2
¶
, ρ
s
=
γ p
s
T
s
,
где p
2
, u
z2
, T
2
, c
2
— давление, скорость, температура и скорость звука за
ударной волной, которые мы получаем из условий Ренкина-Гюгонио [3]:
ρ
2
= ρ
1
(γ + 1)Ma
2
1
2 + (γ − 1)Ma
2
1
, p
2
= p
1
2γMa
2
1
− (γ − 1)
γ + 1
,
(5.8.8)
u
z2
= u
z1
2 + (γ − 1)Ma
2
1
(γ + 1)Ma
2
1
, T
2
= γ
p
2
ρ
2
, c
2
=
p
T
2
,
здесь ρ
1
, u
z1
, p
1
, T
1
— известные параметры набегающего потока. Мак-
симальное значение плотности в ударной волне, согласно (5.8.8), опреде-
ляется как ρ
max
= (γ + 1)/(γ − 1), и для γ = 5/3 составляет ρ
max
= 4.

94Глава 5. Численные алгоритмы решения нестационарных задач газовой динамики
Расстояние между ударной волной и торцом цилиндра S можно оце-
нить на основе аппроксимационной формулы Лунева [48].
S = R
c
√
k (1 + 0.6 k), k =
ρ
1
ρ
2
, (5.8.9)
где ρ
1
= ρ
∞
— плотность на входной границе, ρ
2
— плотность за ударной
волной, рассчитанная по условиям Гюгонио (5.8.8). Положение ударной
волны в расчете можно определять по положению звуковой линии, то
есть линии, на которой локальное число Маха Ma = 1. Теоретические
значения положения ударной волны помещены в табл. 5.2.
Ma 1.5 2 3 5 50
S 1.03 0.84 0.69 0.62 0.58
Таблица 5.2: Положение ударной волны
Расчеты проведены на равномерных пространственных сетках с ша-
гами h
r
= h
z
= 0.05 и h
r
= h
z
= 0.025 для чисел Маха Ma =
1.5, 2, 3, 5, 50 и различных значений параметра α. В Таблице 5.3 приве-
дены характеристики расчетов и сопоставление полученных в расчетах
параметров торможения с теоретическими значениями (выделены жир-
ным шрифтом).
Для всех чисел Маха, включая Ma = 50, полученные в расчете зна-
чения параметров торможения соответствуют теоретическим значениям,
рассчитанным по формулам (5.8.8).
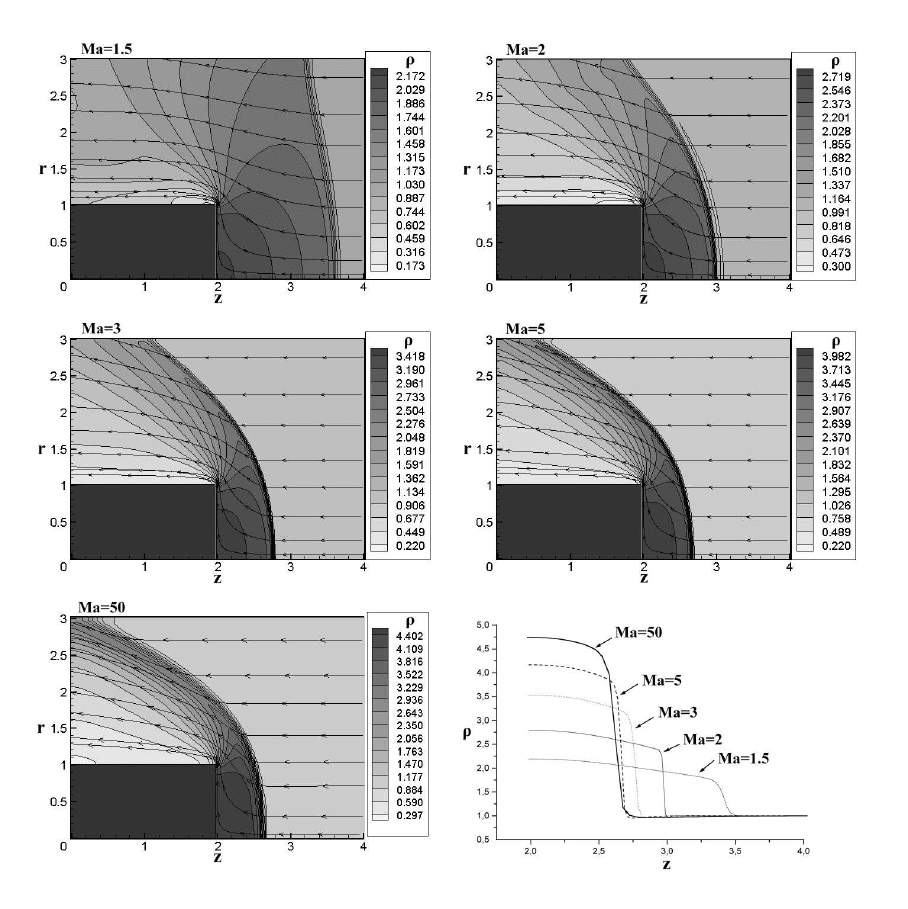
Распределение плотности и линии тока на момент установления стаци-
онарного течения для вариантов с числами Маха 1.5, 2, 3, 5 и 50 (α = 0.5
и α = 1 ) приведены на рис. 5.7. Там же показано изменение формы и
положения ударной волны и структуры течения с ростом скорости набе-
гающего потока (числа Маха). Полученные в расчетах значения положе-
ния ударных волн качественно cовпадают с теоретическими значениями
из табл. 5.2. Диапазон изменения давления значительно изменяется с ро-
стом числа Маха, что наглядно демонстрирует формула (5.8.8). Так, для
Ma = 1.5 давление торможения составляет p
s
= 2.28, а для Ma = 50
увеличивается на три порядка до p
s
= 2203.6.
На приведенных графиках видна высокая точность расчета скачков
уплотнения и отсутствие осцилляций решения при больших числах Ma.
Оптимальным с точки зрения точности и эффективности алгоритма
значением численного коэффициента является α = 0.5. Скорость схо-
димости практически не зависит от параметра α. При больших числах
5.8. Задача о течении в окрестности цилиндра 95
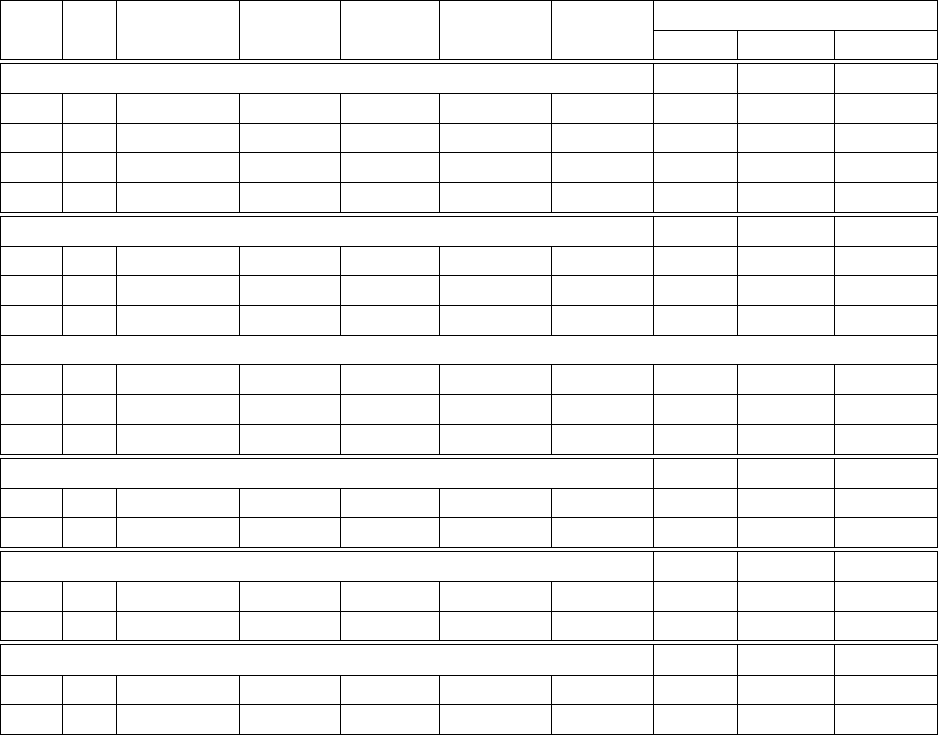
Невязка Число Параметры торможения
Ma α Сетка h
r
= h
z
∆t ² шагов ρ
s
p
s
T
s
Теоретические значения для Ma = 1.5
∗)
2.172 2.280 1.750
1.5 1.0 120 × 120 0.05 10
−3
10
−5
28 034 2.112 2.248 1.774
1.5 0.5 120 × 120 0.05 10
−3
10
−5
27 363 2.156 2.280 1.763
1.5 0.5 160 × 120 0.025 5 ·10
−4
10
−4
126 000 2.186 2.305 1.757
1.5 0.2 120 × 120 0.05 10
−3
10
−5
27 637 2.189 2.303 1.753
Теоретические значения для Ma = 2
∗)
2.719 3.807 2.333
2 1.0 80 × 60 0.05 10
−3
10
−5
16 255 2.648 3.704 2.331
2 0.5 80 × 60 0.05 10
−3
10
−5
15 473 2.720 3.781 2.317
2 0.2 80 × 60 0.05 10
−3
10
−5
15 961 2.781 3.843 2.303
2 1.0 160 × 120 0 .025 5 · 10
−4
10
−5
30 903 2.717 3.777 2.317
2 0.5 160 × 120 0 .025 5 · 10
−4
10
−5
30 774 2.760 3.818 2.306
2 0.2 160 × 120 0 .025 5 · 10
−4
10
−5
31 494 2.791 3.848 2.298
Теоретические значения для Ma = 3
∗)
3.418 8.204 4.000
3 1.0 160 × 120 0 .025 10
−4
10
−5
90 107 3.457 8.089 3.900
3 0.5 160 × 120 0 .025 10
−4
10
−5
91 504 3.525 8.204 3.879
Теоретические значения для Ma = 5
∗)
3.982 22.330 9.333
5 1.0 160 × 120 0 .025 10
−4
10
−5
57 436 4.076 21.914 8.961
5 0.5 160 × 120 0 .025 10
−4
10
−5
57 505 4.167 22.287 8.914
Теоретические значения для Ma = 50
∗)
4.402 2203.6 834.33
50 1.0 80 × 60 0.05 10
−6
10
−4
125 000 4.756 2181.1 764.35
50 0.5 80 × 60 0.05 5 · 10
−6
10
−4
119 637 4.739 2211.8 777.87
∗)
– теоретические значения рассчитаны по формулам (5.8.8)
Таблица 5.3: Расчет сверхзвукового осесимметричного течения
96Глава 5. Численные алгоритмы решения нестационарных задач газовой динамики
Ma сгущение пространственной сетки приводит к увеличению точности
численного решения.
Рис. 5.7: Распределение плотности в осесимметричном течении
5.9 Задача о течении в плоском канале с уступом
Приведем пример расчета невязкого сверхзвукового течения в канале со
ступенькой. Сложная конфигурация ударных волн, формирующихся с
течением времени в канале, служит известным тестом для оценки рабо-
тоспособности методов высокого порядка точности для решения уравне-
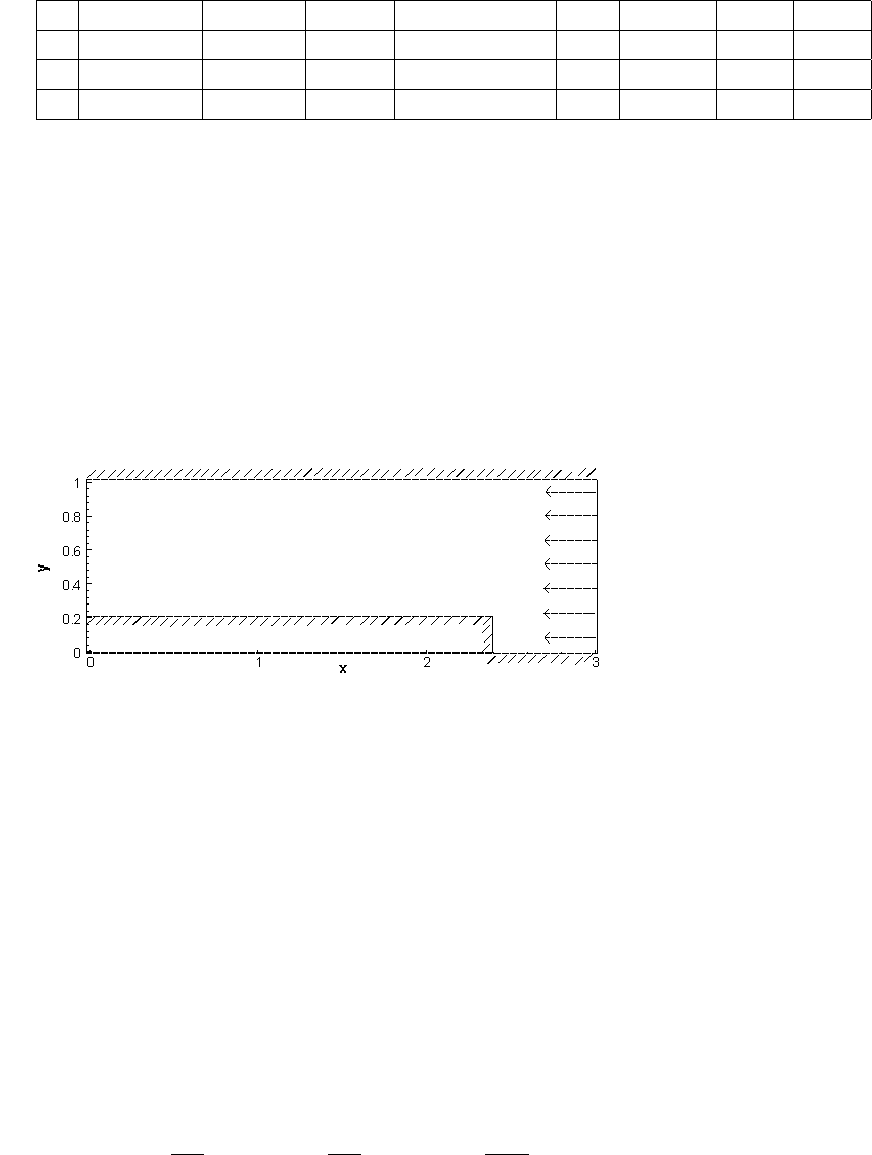
5.9. Задача о течении в плоском канале с уступом 97
V Сетка h
x
= h
y
∆t Число шагов t Время ρ
min
ρ
max
1 120 × 40 0.025 0.001 4000 4 4 мин 0.551 4.464
2 240 × 80 0.0125 0.0005 8000 4 40 мин 0.377 4.553
3 480 ×160 0.00625 0.0001 40000 4 14 ч 0.247 4.595
Таблица 5.4: Расчет течения в канале с уступом
ний Эйлера и Навье–Стокса ([46], [47]).
Задача решается в следующей постановке: длина канала — 3, ширина
— 1, высота ступеньки, расположенной на расстоянии 0.6 от начала ка-
нала, равна 0.2. Рассматривается течение невязкого нетеплопроводного
газа (1/Re = 0) с показателем адиабаты γ = 1.4, Ma = 3. Газ втекает
справа (рис. 5.8).
Рис. 5.8: Схема расчетной области в задаче о течении в канале с уступом
Течение описывается КГД системой, записанной в декартовой систе-
ме координат (5.1.1)–(5.1.4) в безразмерном виде. В качестве начальных
условий используются параметры набегающего потока.
Граничные условия задаются следующим образом. На входной грани-
це значения газодинамических параметров полагаются равными значе-
ниям набегающего потока, то есть ρ = 1, u
x
= −Ma, u
y
= 0 и p = 1 /γ.
На выходной границе задаются "мягкие" граничные условия ∂f/∂x =
0, где f = (ρ, p, u
x
, u
y
). На твердых стенках канала и ступеньки задаются
граничные условия "симметрии":
∂p
∂n
= 0,
∂ρ
∂n
= 0,
∂u
τ
∂n
= 0, u
n
= 0,
где n — нормаль к соответствующей границе. Расчеты проведены на трех
равномерных пространственных сетках. Основные параметры расчетов
представлены в табл. 5.4. При вычислении релаксационного параметра
τ коэффициент α = 0.3.
98Глава 5. Численные алгоритмы решения нестационарных задач газовой динамики
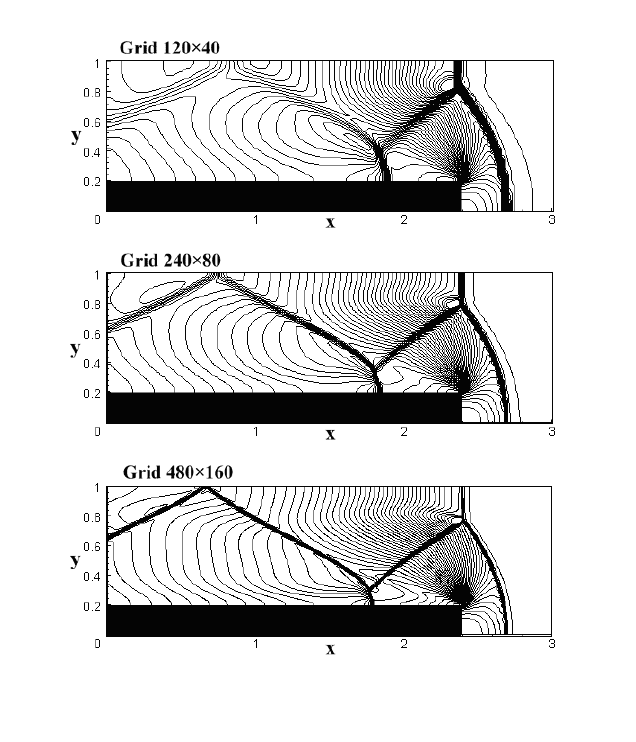
На рис. 5.9 приведены распределение плотности на момент време-
ни t = 4 (50 изолиний расположены эквидистантно), полученные при
расчетах на последовательно сгущающихся сетках: 120 × 40, 240 × 80 и
480 × 160.
Рис. 5.9: Распределения плотности для течения в канале на момент времени t = 4.
Расчеты на трех сгущающихся сетках.
Отчетливо прослеживается образование вторичных волн отражения
от верхней стенки канала и верхней поверхности ступеньки. За волной
разрежения над углом ступеньки плотность газа минимальна, вблизи
контактного разрыва за тройной точкой над уступом плотность газа мак-
симальна. Приведенные рисунки наглядно демонстрируют сходимость
численного решения при сгущении пространственной сетки.
Картина течения, образующаяся на момент времени t = 4,
соответствует данным [47], полученным с использованием кусочно-
параболических схем третьего порядка точности по пространству, и ре-
5.10. Численный алгоритм расчета дозвуковых течений 99
зультатам [46], где применяются методы расщепления первого, второго
и третьего порядка точности.
Полученные в расчетах минимальное и максимальное значения плот-
ности на разных сетках приведены в табл. 5.4. Согласно работе [47], ко-
торая для этой задачи считается эталонной, ρ
max
/ρ
∞
= 4.33, ρ
min
/ρ
∞
=
0.18. Видно, что максимальные значения плотности хорошо совпадают.
При сгущении пространственной сетки величина ρ
min
уточняется.
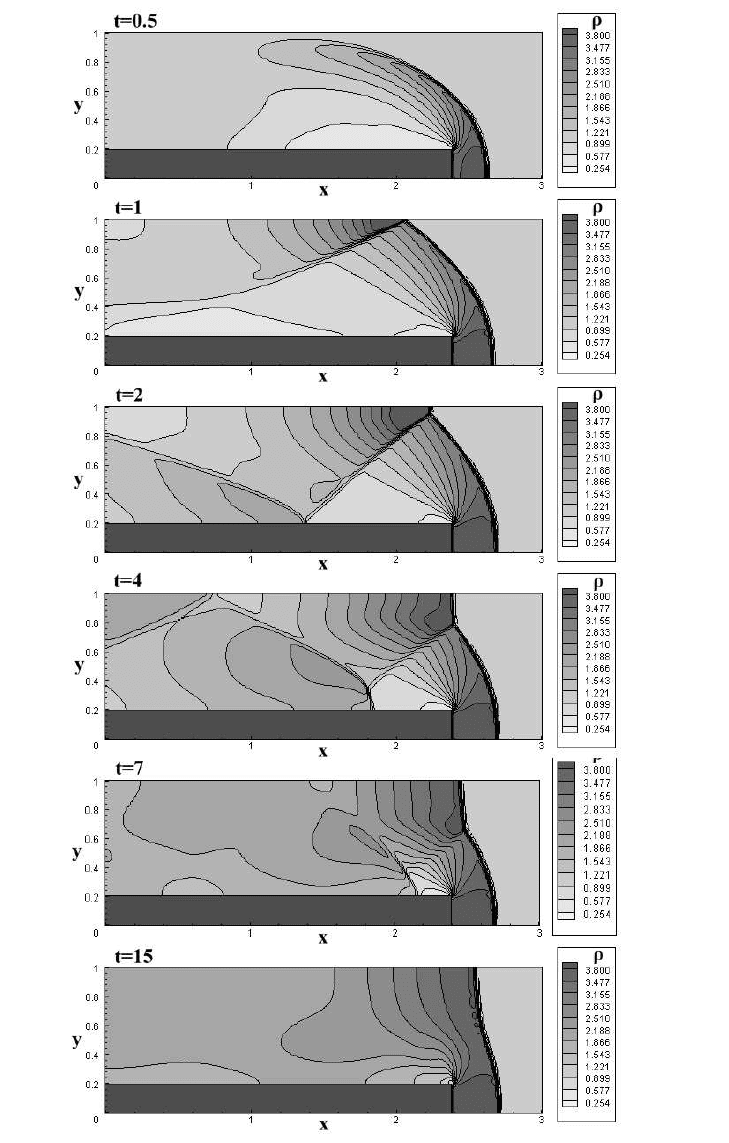
На рис. 5.10 приведен процесс установления течения. Изображено рас-
пределение плотности, полученное на моменты времени t = 0.5, 1, 2, 4,
7, 15 на сетке 240 × 80.
5.10 Численный алгоритм расчета дозвуковых тече-
ний
Если скорость газа в интересующей нас задаче не превосходит скорость
звука, то такие течения не сопровождаются формированием сильных
ударных волн, хотя и в этих течениях могут существовать локальные
сверхзвуковые зоны. Численное моделирование таких дозвуковых тече-
ний имеет свои особенности. В частности это касается способа регуляри-
зации численного решения. В отличие от сверхзвуковых течений, допол-
нительная сложность здесь заключается в постановке условий на свобод-
ных границах.
В данном параграфе изложены особенности численного алгоритма
расчета дозвуковых течений, отличающие этот метод от описанных выше
алгоритмов расчета сверхзвуковых течений.
5.10.1 Безразмерный вид уравнений и введение регуляриза-
ции
При расчете дозвуковых течений, в отличие от сверхзвуковых задач, в
качестве единицы скорости будем выбирать скорость набегающего по-
тока u
∞
. То есть основными размерными параметрами будут плотность
набегающего потока ρ
∞
, скорость набегающего потока u
∞
и характерный
размер — обозначим его через h
0
.
Соотношения между размерными и безразмерными величинами (знак
100Глава 5. Численные алгоритмы решения нестационарных задач газовой динамики
Рис. 5.10: Установление плотности в задаче о течении в канале с уступом
