Лекции - Математические модели и численные методы в динамике жидкости и газа
Подождите немного. Документ загружается.


3.5. Уравнения Навье–Стокса как асимптотика КГД системы 61
КГД добавка для вектора теплового потока
Распишем еще раз левую часть выражения (3.5.7):
E =
u
2
2
M + ρ~u(~u ·
~
∇)~u + εM + ρ(~u ·
~
∇)ε + (~u ·
~
∇)p + p div ~u.
Откуда выразим
ρ(~u ·
~
∇)ε + p div ~u = E −M
µ
ε +
u
2
2
¶
− ρ~u(~u ·
~
∇)~u − (~u ·
~
∇)p.
Из (3.5.5) выразим div ~u
div ~u =
M − (~u ·
~
∇)ρ
ρ
=
M
ρ
+ ρ(~u ·
~
∇)
µ
1
ρ
¶
. (3.5.19)
Учитывая (3.5.16) и (3.5.19), получим
ρ(~u ·
~
∇)ε + pρ(~u ·
~
∇)
µ
1
ρ
¶
= E − M
µ
ε −
u
2
2
−
p
ρ
¶
− (~u ·
~
I). (3.5.20)
Из (3.5.20) и (3.5.4) следует, что
~q
QGD
= τ~u
·
E −M
µ
ε −
u
2
2
−
p
ρ
¶
− (~u ·
~
I)
¸
. (3.5.21)
и ~q
QGD
∼ o(τ
2
).
Это означает, что для стационарных течений КГД уравнения аппрок-
симируют систему уравнений Навье–Стокса с точностью O(τ
2
). Таким
образом можно полагать, что при стремлении величины τ к нулю, реше-
ние КГД уравнений с соответствующим порядком сходится к решению
системы уравнений Навье–Стокса. Заметим, что для нестационарных те-
чений аппроксимацию второго порядка доказать не удается.
Другой важной асимптотикой уравнений гидродинамики является
приближение пограничного слоя [2], [3]. Было показано (см., например,
[7], [30], [60] ) что приближением пограничного слоя для КГД уравнений,
так же как и для уравнений Навье–Стокса, служат уравнения Прандтля.

Глава 4
КГД уравнения и системы координат
В этой главе КГД уравнения выписаны в тензорно-индексном представ-
лении в произвольных координатах. Приведенный вид уравнений позво-
ляет не только выписать КГД систему в удобной для решения задачи
системе координат, но также дает возможность строить разностные ап-
проксимации уравнений на ортогональных пространственных сетках в
преобразованном пространстве координат [20].
В последних параграфах КГД уравнения выписаны в декартовой и
цилиндрической системах координат.
4.1 Запись КГД уравнений в произвольной системе
координат
Для дальнейших выкладок нам понадобятся некоторые теоретические
сведения [135, 136, 137].
Рассмотрим в евклидовом пространстве некоторый базис ~e
j
, любой
вектор в котором задается координатами (x
1
, x
2
, x
3
). Пусть ~r
i
— новый
базис, любой вектор в котором задается координатами (bx
1
, bx
2
, bx
3
).
Определим переход от базиса ~e
j
к новому базису ~r
i
с помощью следу-
ющего преобразования (здесь и далее подразумевается суммирование по
повторяющимся индексам):
~r
i
= b
j
i
~e
j
, b
j
i
=
∂x
j
∂bx
i
, (4.1.1)
где b
j
i
— матрица перехода от базиса ~e
j
к базису ~r
i
.
В дифференциальной геометрии и тензорном анализе вводится поня-
тие метрического тензора, который отражает дифференциальные свой-
ства внутренней геометрии области. Компоненты метрического тензора
определяются как:
g
ij
=
∂x
k
∂bx
i
∂x
k
∂bx
j
, (4.1.2)
62

4.1. Запись КГД уравнений в произвольной системе координат 63
g ≡ det(g
ij
) — определитель метрического тензора.
Рассмотрим некоторый вектор
~
U = U
i
~e
i
в базисе ~e
i
, где U
i
— коорди-
наты вектора в данном базисе. При переходе к новому нормированному
базису (
b
~e
i
= ~r
i
/
p
|g
ii
|) координаты вектора
~
U преобразуются по следую-
щей формуле:
b
U
j
= U
i
¯
b
j
i
q
|g
jj
|, U
i
=
b
U
j
p
|g
jj
|
b
i
j
, (4.1.3)
где
¯
b = b
−1
— матрица обратного перехода от базиса ~r
i
к базису ~e
j
.
Координаты вектора
b
U
i
в нормированном базисе
b
~e
j
связаны с коор-
динатами вектора U
i
в базисе ~r
i
следующим соотношением:
b
U
i
=
p
|g
ii
|U
i
. (4.1.4)
Аналогичная формула для компонент тензора Π
ik
имеет вид:
b
Π
ik
=
p
|g
ii
| |g
kk
|Π
ik
. (4.1.5)
В формулах (4.1.4) и (4.1.5) суммирование по повторяющимся индек-
сам не производится.
Теперь выпишем формулы тензорного анализа, необходимые для
представления КГД системы уравнений в тензорно-индексном виде.
Скалярное произведение векторов:
(
~
A ·
~
B) = g
kl
A
k
B
l
. (4.1.6)
Ковариантная и контравариантная производная скалярной функ-
ции:
∇
i
A =
∂A
∂x
i
, ∇
i
A = g
ij
∇
j
A. (4.1.7)
Ковариантная производная тензора первого и второго ранга:
∇
j
U
i
=
∂U
i
∂x
j
+ U
m
Γ
i
mj
, (4.1.8)
∇
i
A
ij
=
∂A
ij
∂x
i
+ Γ
i
li
A
lj
+ Γ
j
mi
A
im
, (4.1.9)
где
Γ
k
ij
=
1
2
g
kl
µ
∂g
lj
∂x
i
+
∂g
il
∂x
j
−
∂g
ij
∂x
l
¶
(4.1.10)
— символы Кристоффеля второго рода.

64 Глава 4. КГД уравнения и системы координат
Дивергенция вектора (частный случай (4.1.8) при i = j):
∇
i
A
i
=
1
p
|g|
∂(
p
|g|A
i
)
∂x
i
. (4.1.11)
В дальнейшем мы рассматриваем ортогональные системы координат,
в которых элементы метрических тензоров подчиняются условию g
ik
=
g
ii
δ
i
k
, где δ
i
k
— символ Кронекера, для которого
δ
i
k
=
½
1, если i = k
0, если i 6= k
.
В системе ортогональных координат для вычисления символов Кри-
стоффеля Γ
k
ij
справедливы следующие соотношения:
Γ
k
ij
= 0 (i 6= j, j 6= k, k 6= i), (4.1.12)
Γ
k
ii
= −
1
2g
kk
∂g
ii
∂x
k
(i 6= k), (4.1.13)
Γ
k
ik
= Γ
k
ki
=
1
2g
kk
∂g
kk
∂x
i
=
1
2
∂(ln g
kk
)
∂x
i
. (4.1.14)
Выпишем систему КГД уравнений в тензорно-индексном представле-
нии.
Уравнение баланса массы имеет вид:
∂ρ
∂t
+
1
p
|g|
∂
∂x
i
(
p
|g|j
i
m
) = 0, (4.1.15)
где вектор плотности потока массы определяется как
j
i
m
= ρ
Ã
b
U
i
p
|g
ii
|
− w
i
!
,
w
i
=
τ
ρ
"
∂
∂x
j
Ã
ρ
b
U
j
p
|g
jj
|
b
U
i
p
|g
ii
|
!
+ Γ
j
lj
ρ
b
U
l
p
|g
ll
|
b
U
i
p
|g
ii
|
#
+
+
τ
ρ
"
Γ
i
mj
ρ
b
U
m
p
|g
mm
|
b
U
j
p
|g
jj
|
+ g
ij
∂p
∂x
j
#
.
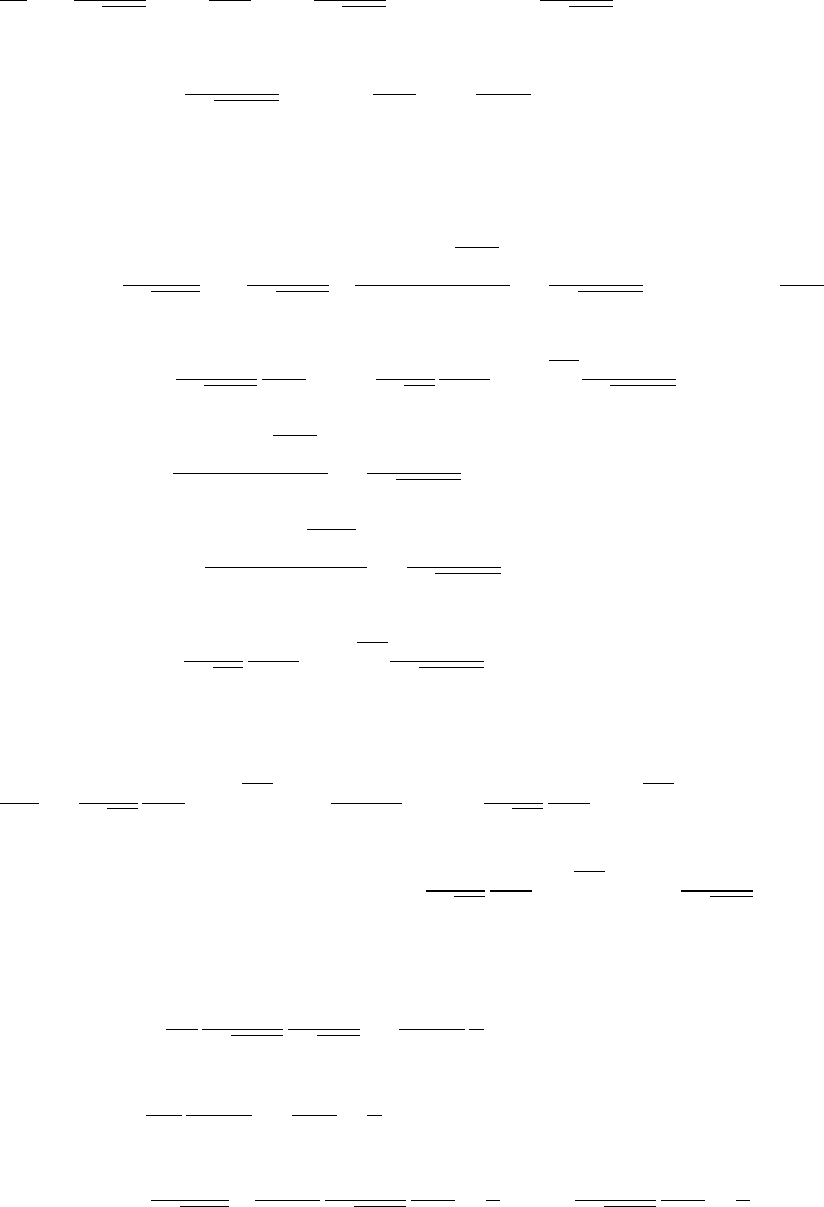
4.1. Запись КГД уравнений в произвольной системе координат 65
Уравнение баланса импульса записывается следующим образом
∂
∂t
Ã
ρ
b
U
i
p
|g
ii
|
!
+
∂
∂x
j
Ã
j
j
m
b
U
i
p
|g
ii
|
!
+ Γ
j
lj
Ã
j
l
m
b
U
i
p
|g
ii
|
!
+
+ Γ
i
mj
Ã
j
j
m
b
U
m
p
|g
mm
|
!
+ g
ij
∂p
∂x
j
=
∂Π
ji
∂x
j
+ Γ
j
lj
Π
li
+ Γ
i
mj
Π
jm
, (4.1.16)
а компоненты тензора вязких напряжений определяются по формулам
Π
ji
=Π
ji
NS
+
+ τ
b
U
j
p
|g
jj
|
(
ρ
b
U
k
p
|g
kk
|
"
∂(
b
U
i
/
p
|g
ii
|)
∂x
k
+
b
U
m
p
|g
mm
|
Γ
i
mk
#
+ g
ik
∂p
∂x
k
)
+
+ τg
ji
"
b
U
k
p
|g
kk
|
∂p
∂x
k
+ γp
1
p
|g|
∂
∂x
m
Ã
p
|g|
b
U
m
p
|g
mm
|
!#
,
Π
ji
NS
=η
(
g
jk
"
∂(
b
U
i
/
p
|g
ii
|)
∂x
k
+
b
U
m
p
|g
mm
|
Γ
i
mk
#)
+
+ η
(
g
ik
"
∂(
b
U
j
/
p
|g
jj
|)
∂x
k
+
b
U
m
p
|g
mm
|
Γ
j
mk
#
−
− 2/3g
ji
1
p
|g|
∂
∂x
m
Ã
p
|g|
b
U
m
p
|g
mm
|
!)
.
Уравнение баланса энергии имеет вид:
∂E
∂t
+
1
p
|g|
∂
∂x
j
µ
p
|g|j
j
m
µ
E + p
ρ
¶¶
+
1
p
|g|
∂
∂x
j
³
p
|g|q
j
´
=
=
1
p
|g|
∂
∂x
j
(
p
|g|g
kl
Π
jk
b
U
l
p
|g
ll
|
), (4.1.17)
где энергия и тепловой поток записываются как
E = ρ
Ã
g
kl
2
b
U
k
p
|g
kk
|
b
U
l
p
|g
ll
|
+
1
γ − 1
p
ρ
!
,
q
j
= −
η
P r
γ
γ − 1
g
jk
∂
∂x
k
µ
p
ρ
¶
−
− τ ρ
b
U
j
p
|g
jj
|
"
1
γ − 1
b
U
k
p
|g
kk
|
∂
∂x
k
µ
p
ρ
¶
+ p
b
U
k
p
|g
kk
|
∂
∂x
k
µ
1
ρ
¶
#
.
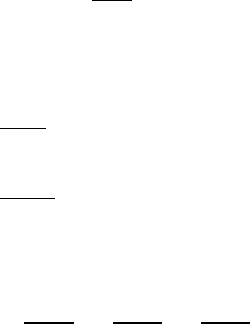
66 Глава 4. КГД уравнения и системы координат
Тензорно-индексный вид (4.1.15)–(4.1.17) позволяет адаптировать
КГД систему уравнений к произвольным системам координат: декарто-
вым, цилиндрическим, сферическим, эллипсоидальным и другим.
4.2 КГД уравнения в декартовой системе координат
В декартовой системе координат положим
bx
1
= x, bx
2
= y, bx
3
= z.
Метрический тензор имеет диагональный вид:
g
ij
=
1 0 0
0 1 0
0 0 1
, g ≡ det g
ij
= 1. (4.2.1)
Формулы (4.1.6) — (4.1.11) принимают более простой вид:
Скалярное произведение векторов:
(
~
A ·
~
B) = A
i
B
i
. (4.2.2)
Прямое тензорное произведение векторов:
(
~
A ⊗
~
B) = A
i
B
j
. (4.2.3)
Производная скалярной функции (градиент):
grad p = ∇
i
p = ∇
i
p =
∂p
∂ˆx
i
. (4.2.4)
Производная тензора первого и второго ранга:
∇
j
A
i
=
∂A
i
∂ˆx
j
, (4.2.5)
∇
j
Π
ij
=
∂Π
ij
∂ˆx
i
. (4.2.6)
Дивергенция:
div
~
A = (
~
∇ ·
~
A) = ∇
i
A
j
=
∂A
x
∂x
+
∂A
y
∂y
+
∂A
z
∂z
, (4.2.7)
div Π = (
~
∇ · Π) = ∇
i
Π
ij
. (4.2.8)
Дивергенция от прямого тензорного произведения:
div(
~
A ⊗
~
B) = ∇
i
(A
i
B
j
). (4.2.9)

4.2. КГД уравнения в декартовой системе координат 67
Дивергенция от скалярного произведения тензора и вектора:
div(Π ·
~
A) = (
~
∇ · (Π ·
~
A)) = ∇
i
(Π
ij
~
A
j
). (4.2.10)
Система КГД уравнений (4.1.15)–(4.1.17) запишется в виде:
∂
∂t
ρ + ∇
i
j
i
m
= 0, (4.2.11)
∂
∂t
(ρ u
j
) + ∇
i
¡
j
i
m
u
j
¢
+ ∇
j
p = ∇
i
Π
ij
, (4.2.12)
∂
∂t
·
ρ
µ
~u
2
2
+ ε
¶¸
+ ∇
i
½
j
i
m
·µ
~u
2
2
+ ε
¶
+
p
ρ
¸¾
+ ∇
i
q
i
= ∇
i
(Π
ij
u
j
).
(4.2.13)
Здесь компоненты вектора плотности потока массы
~
j
m
имеют вид:
j
mx
= j
1
m
= ρu
x
− τ
µ
∂(ρu
2
x
)
∂x
+
∂(ρu
x
u
y
)
∂y
+
∂(ρu
x
u
z
)
∂z
+
∂p
∂x
¶
,
j
my
= j
2
m
= ρu
y
− τ
Ã
∂(ρu
x
u
y
)
∂x
+
∂(ρu
2
y
)
∂y
+
∂(ρu
y
u
z
)
∂z
+
∂p
∂y
!
, (4.2.14)
j
mz
= j
3
m
= ρu
z
− τ
µ
∂(ρu
x
u
z
)
∂x
+
∂(ρu
y
u
z
)
∂y
+
∂(ρu
2
z
)
∂z
+
∂p
∂z
¶
.
В формулах (4.2.14) первые слагаемые соответствуют вектору плот-
ности потока массы Навье–Стокса, а последующие (с множителем τ в
качестве коэффициента) представляют собой КГД добавки.
Элементы тензора вязких напряжений Π имеют вид:
Π
xx
= Π
11
, Π
xy
= Π
12
, Π
xz
= Π
33
,
Π
yx
= Π
21
, Π
yy
= Π
22
, Π
yz
= Π
32
, (4.2.15)
Π
zx
= Π
31
, Π
zy
= Π
32
, Π
zz
= Π
33
,
Π
xx
= η
µ
2
∂u
x
∂x
−
·
2
3
−
ζ
η
¸
div ~u
¶
+ τρu
x
µ
u
x
∂u
x
∂x
+ u
y
∂u
x
∂y
+ u
z
∂u
x
∂z
¶
+
+ τ
µ
2u
x
∂p
∂x
+ u
y
∂p
∂y
+ u
z
∂p
∂z
¶
+ τγp div ~u,
Π
xy
= η
µ
∂u
y
∂x
+
∂u
x
∂y
¶
+ τ ρu
x
µ
u
x
∂u
y
∂x
+ u
y
∂u
y
∂y
+ u
z
∂u
y
∂z
+
1
ρ
∂p
∂y
¶
,

68 Глава 4. КГД уравнения и системы координат
Π
xz
= η
µ
∂u
z
∂x
+
∂u
x
∂z
¶
+ τρu
x
µ
u
x
∂u
z
∂x
+ u
y
∂u
z
∂y
+ u
z
∂u
z
∂z
+
1
ρ
∂p
∂z
¶
,
Π
yx
= η
µ
∂u
x
∂y
+
∂u
y
∂x
¶
+ τρu
y
µ
u
x
∂u
x
∂x
+ u
y
∂u
x
∂y
+ u
z
∂u
x
∂z
+
1
ρ
∂p
∂x
¶
,
Π
yy
= η
µ
2
∂u
y
∂y
−
·
2
3
−
ζ
η
¸
div ~u
¶
+ τ ρu
y
µ
u
x
∂u
y
∂x
+ u
y
∂u
y
∂y
+ u
z
∂u
y
∂z
¶
+
+ τ
µ
u
x
∂p
∂x
+ 2 u
y
∂p
∂y
+ u
z
∂p
∂z
¶
+ τγp div ~u,
Π
yz
= η
µ
∂u
z
∂y
+
∂u
y
∂z
¶
+ τρu
y
µ
u
x
∂u
z
∂x
+ u
y
∂u
z
∂y
+ u
z
∂u
z
∂z
+
1
ρ
∂p
∂z
¶
,
Π
zx
= η
µ
∂u
x
∂z
+
∂u
z
∂x
¶
+ τρu
z
µ
u
x
∂u
x
∂x
+ u
y
∂u
x
∂y
+ u
z
∂u
x
∂z
+
1
ρ
∂p
∂x
¶
,
Π
zy
= η
µ
∂u
y
∂z
+
∂u
z
∂y
¶
+ τρu
z
µ
u
x
∂u
y
∂x
+ u
y
∂u
y
∂y
+ u
z
∂u
y
∂z
+
1
ρ
∂p
∂y
¶
,
Π
zz
= η
µ
2
∂u
z
∂z
−
·
2
3
−
ζ
η
¸
div ~u
¶
+ τρu
z
µ
u
x
∂u
z
∂x
+ u
y
∂u
z
∂y
+ u
z
∂u
z
∂z
¶
+
+ τ
µ
u
x
∂p
∂x
+ u
y
∂p
∂y
+ 2 u
z
∂p
∂z
¶
+ τγp div ~u.
В выражениях для компонент тензора вязких напряжений (4.2.15) слага-
емые с множителем η соответствуют тензору Навье–Стокса, а слагаемые
с множителем τ представляют собой КГД добавки.
Компоненты вектора теплого потока ~q.
q
x
= q
1
= −η
γ
γ − 1
1
P r
∂
∂x
µ
p
ρ
¶
−
− τ ρu
x
1
γ − 1
·
u
x
∂
∂x
µ
p
ρ
¶
+ u
y
∂
∂y
µ
p
ρ
¶
+ u
z
∂
∂z
µ
p
ρ
¶¸
−
− τ ρu
x
p
·
u
x
∂
∂x
µ
1
ρ
¶
+ u
y
∂
∂y
µ
1
ρ
¶
+ u
z
∂
∂z
µ
1
ρ
¶¸
,
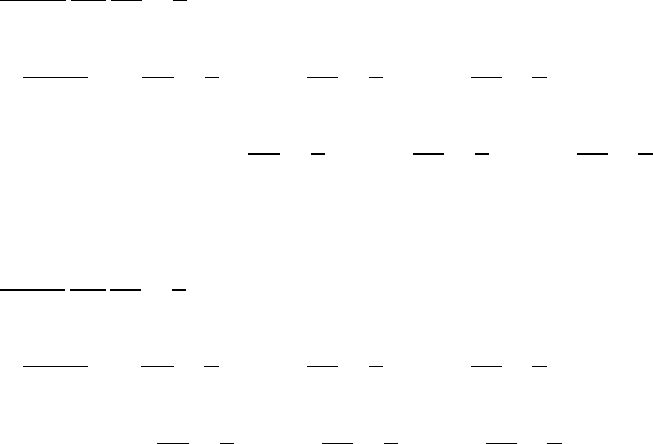
4.3. КГД уравнения в цилиндрической системе координат 69
q
y
= q
2
= −η
γ
γ − 1
1
P r
∂
∂y
µ
p
ρ
¶
−
− τ ρu
y
1
γ − 1
·
u
x
∂
∂x
µ
p
ρ
¶
+ u
y
∂
∂y
µ
p
ρ
¶
+ u
z
∂
∂z
µ
p
ρ
¶¸
−
− τ ρu
y
p
·
u
x
∂
∂x
µ
1
ρ
¶
+ u
y
∂
∂y
µ
1
ρ
¶
+ u
z
∂
∂z
µ
1
ρ
¶¸
,
q
z
= q
3
= −η
γ
γ − 1
1
P r
∂
∂z
µ
p
ρ
¶
−
− τ ρu
z
1
γ − 1
·
u
x
∂
∂x
µ
p
ρ
¶
+ u
y
∂
∂y
µ
p
ρ
¶
+ u
z
∂
∂z
µ
p
ρ
¶¸
−
− τ ρu
z
p
·
u
x
∂
∂x
µ
1
ρ
¶
+ u
y
∂
∂y
µ
1
ρ
¶
+ u
z
∂
∂z
µ
1
ρ
¶¸
. (4.2.16)
В выражениях для компонент вектора теплового потока ~q (4.2.16), как и в
предыдущих случаях, слагаемые с множителем η соответствуют системе
Навье–Стокса, с множителем τ являются КГД добавками.
4.3 КГД уравнения в цилиндрической системе коор-
динат
В цилиндрической системе координат положим
bx
1
= r, bx
2
= ϕ, bx
3
= z.
Метрический тензор имеет диагональный вид:
g
ij
=
1 0 0
0 r
2
0
0 0 1
, (4.3.1)
а его определитель равен g ≡ det g
ij
= r
2
.
Воспользуемся приведенными выше формулами тензорного анали-
за (4.1.4)–(4.1.11) и выпишем r, ϕ, z–компоненты вектора плотности по-
тока массы
~
j
m
, тензора вязких напряжений Π и вектора теплового потока
~q.
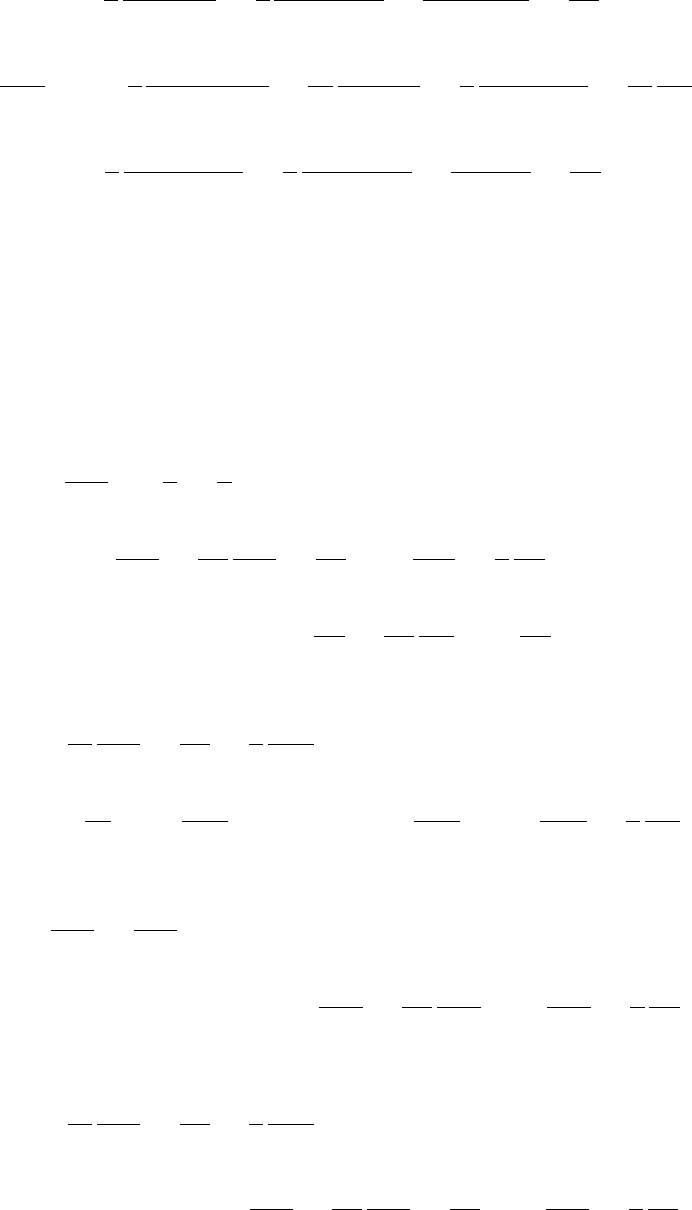
70 Глава 4. КГД уравнения и системы координат
Компоненты вектора плотности потока массы
~
j
m
:
j
mr
= j
1
m
= ρu
r
− τ
µ
1
r
∂(rρu
2
r
)
∂r
+
1
r
∂(ρu
r
u
ϕ
)
∂ϕ
+
∂(ρu
r
u
z
)
∂z
+
∂p
∂r
¶
,
j
mϕ
= rj
2
m
=
ρu
ϕ
r
− τ
Ã
1
r
∂(rρu
ϕ
u
r
)
∂r
+
1
r
2
∂(ρu
2
ϕ
)
∂ϕ
+
1
r
∂(ρu
ϕ
u
z
)
∂z
+
1
r
2
∂p
∂ϕ
!
,
j
mz
= j
3
m
= ρu
z
− τ
µ
1
r
∂(rρu
z
u
r
)
∂r
+
1
r
∂(ρu
z
u
ϕ
)
∂ϕ
+
∂(ρu
2
z
)
∂z
+
∂p
∂z
¶
.
В каждой из вышеприведенных формул первое слагаемое правой ча-
сти соответствует вектору потока массы Навье–Стокса
~
j
NS
m
, а последу-
ющие (с множителем τ в качестве коэффициента) представляют собой
КГД добавки
~
j
QGD
m
.
Элементы тензора вязких напряжений Π имеют вид:
Π
rr
= Π
11
= η
µ
2
∂u
r
∂r
−
·
2
3
−
ζ
η
¸
div ~u
¶
+
+ τρu
r
µ
u
r
∂u
r
∂r
+
u
ϕ
r
∂u
r
∂ϕ
−
u
ϕ
r
+ u
z
∂u
r
∂z
+
1
ρ
∂p
∂r
¶
+
+ τ
µ
u
r
∂p
∂r
+
u
ϕ
r
3
∂p
∂ϕ
+ u
z
∂p
∂z
+ γp div ~u
¶
,
Π
rϕ
= rΠ
12
= η
µ
1
r
2
∂u
r
∂ϕ
−
u
ϕ
r
2
+
1
r
∂u
ϕ
∂r
¶
+
+ τρ
u
r
r
µ
ru
r
∂u
ϕ
∂r
− r
2
u
r
u
ϕ
+ u
ϕ
∂u
ϕ
∂ϕ
+ ru
z
∂u
ϕ
∂z
+
1
ρ
∂p
∂ϕ
¶
,
Π
rz
= Π
13
= η
µ
∂u
r
∂z
+
∂u
z
∂r
¶
+
+ τρu
r
µ
u
r
∂u
z
∂r
+
u
ϕ
r
∂u
z
∂ϕ
+ u
z
∂u
z
∂z
+
1
ρ
∂p
∂z
¶
,
Π
ϕr
= rΠ
21
= η
µ
1
r
2
∂u
r
∂ϕ
−
u
ϕ
r
2
+
1
r
∂u
ϕ
∂r
¶
+
+ τρu
ϕ
Ã
u
r
∂u
r
∂r
+
u
ϕ
r
∂u
r
∂ϕ
−
u
2
ϕ
r
+ u
z
∂u
r
∂z
+
1
ρ
∂p
∂r
!
,
