Lee K.K. Lectures on Dynamical Systems, Structural Stability and Their Applications
Подождите немного. Документ загружается.


chaos.
Within
an
entrainment
horn,
they
observed
symmetry
breaking,
period
doubling,
and
complementary
band
merging.
Very
recently,
Gunaratne
et
al
[1989]
have
studied
the
chaotic
dynamics
from
a
nonlinear
electronic
cirsuit
which
has
shown
to
exhibit
the
universal
topological
structure
of
maps
on
an
annulus.
They
further
suggested
that
low-dimensional
strange
attractors
fall
into
a
few
classes,
each
characterized
by
distinct
universal
topological
features.
Recently,
Holmes
[1986]
(using
the
averaging
method)
and
Melnikov
[1963]
(using
the
perturbation
technique)
have
shown
that
an
N-degree
of
freedom
model
of
weakly
nonlinear
surface
waves
due
to
Miles
[1976]
has
transverse
homoclinic
orbits.
And
this
implies
that
sets
of
chaotic
orbits
exist
in
the
phase
space.
Relevance
of
their
results
to
experimental
work
on
parametrically
excited
surface
waves
[Ciliberto
and
Gollub
1985)
are
also
briefly
discussed.
Funakoshi
and
Inoue
[1987]
have
experimentally
demonstrated
the
chaotic
behavior
of
the
surface
water
wave,
modeled
by
Miles
[1976]
with
the
assumption
of
weak
nonlinearity
and
linear
damping,
when a
container
is
oscillated
resonantly
in
a
horizontal
direction
with
appropriate
amplitude
and
frequency.
The
experimental
work
of
Funakoshi
and
Inoue
[1987]
are
directly
relevant
to
Holmes'
[1986]
results,
yet
they
are
not
aware
of
Holmes•
work.
Melnikov•s
method
detects
transverse
homoclinic
points
in
differential
equations
which
are
small
perturbations
of
integrable
systems.
This
together
with
the
Smale-Birkhoff
homoclinic
theorem
[Smale
1967]
implies
the
existence
of
chaotic
motions
among
the
solutions
of
the
equation
with
qualitative
information.
Recently,
Brunsden
and
Holmes
[1987]
proposed
a
method
which
provides
quantitative
statistical
measures
of
solutions.
They
compute
power
spectra
of
chaotic
motions
which
are
perturbations
of
homoclinic
orbits
and
their
approach
relies
on
the
existence
of
global
homoclinic
structures,
verified
by
Melnikov
theory,
and
derived
from
the
notion
of
coherent
structures
284

in
turbulence
theory.
Another
example
of
the
route
to
chaos
via
period-doubling
is
a
linear,
viscously
damped
oscillator
which
rebounds
elastically
whenever
the
displacement
drops
to
zero.
It
exhibits
a
family
of
subharmonic
resonant
peaks
between
which
there
are
cascades
of
period-doubling
bifurcations
leading
to
chaotic
regimes
[Thompson
and
Ghaffari
1982].
Yet
another
example
of
routes
to
chaos
is
the
chaotic
scattering.
Bleher
et
al
(1989]
have
shown
that
the
onset
of
chaotic
behavior
in
a
class
of
classical
scattering
problems
could
occur
in
two
possible
ways.
One
is
abrupt
and
is
related
to
a
change
in
the
topology
of
the
energy
surface,
while
the
other
is
a
result
of
a
complex
sequence
of
saddle-node
and
period-
doubling
bifurcations.
The
former,
the
abrupt
bifurcation
represents
a
new
generic
route
to
chaos
and
yields
a
characteristic
scaling
of
the
fractal
dimension
associated
with
the
scattering
function
as
[ln(Ec
-
E)-
1
]-
1
,
for
particle
energies
E
near
the
critical
value
Ec
at
which
the
scattering
becomes
chaotic.
It
is
known
that
steady
planar
propagation
of
a
combustion
front
is
unstable
to
disturbances
corresponding
to
pulsating
and
spinning
waves.
Recently,
Margolis
and
Matckowsky
(1988]
considered
the
nonlinear
evolution
equations
for
the
amplitudes
of
the
pulsating
and
spinning
waves
in
a
neighborhood
of
a
double
eigenvalue
of
the
system,
in
particular,
near
a
degenerate
Hopf
bifurcation
point,
and
new
quasi-periodic
modes
of
combustion
were
also
described.
1/f
noise
is
found
ubiquitously
in
various
scientific
and
engineering
disciplines.
It
has
been
speculated
whether
1/f
noise
can
be
explained
as
a
chaotic
phenomenon.
Recently,
Geisel,
Zacher!
and
Radons
(1987]
proposed
a
new
mechanism
for
1/f
noise
as
a
generic
phenomenon
in
the
velocity
fluctuations
of
a
particle
in
a
2-dim
periodic
potential,
and
is
closely
related
to
the
generic
structure
of
phase
space
of
nonintegrable
Hamiltonian
systems.
on
the
285

other
hand,
Bak,
Tang
and
Wiesenfeld
[1987]
have
shown
that
dynamical
systems
with
spatial
degrees
of
freedom
naturally
evolve
into
a
self-organized
critical
state
and
1/f
(or
flicker)
noise
can
be
identified
with
the
dynamics
of
the
critical
state.
They
also
related
this
to
fractal
objects.
Phase
transitions
of
trapped
particles
and
ions,
initially
observed
in
1959
by
collisional
cooling
and
more
recently
by
laser
cooling,
can
also
be
explained
as
order-chaos
transitions
[Hoffnagle
et
al
1988].
In
the
following
we
shall
briefly
discuss
one
of
the
well-known
examples
of
deterministic
chaos,
the
Lorenz
model
of
turbulence.
For
details,
see
Guckenheimer
and
Holmes
[1983].
c.
Sparrow
[1982]
gives
an
extensive
treatment
of
Lorenz
equations.
There
are
several
other
well-known
examples
of
deterministic
chaos,
such
as
Vander
Pol's
equations
of
damped
nonlinear
oscillator
[see,
e.g.,
Holmes
1979,
Holmes
and
Rand
1978],
Cuffing's
equations
of
nonlinear
mechanical
oscillator
with
a
cubic
stiffness
[Novak
and
Frehlich
1982,
Liu
and
Young
1986],
we
either
have
touched
upon
earlier
or
we
shall
meet
in
next
chapter.
For
a
nice
review,
see,
e.g.,
Holmes
and
Moon
[1983].
We
will
not
be
able
to
get
into
any
detail
to
discuss
their
routes
to
chaos.
For
details,
once
again
the
reader
is
referred
to
Guckenheimer
and
Holmes
[1983]
and
Moon
[1987].
Recently,
Byatt-Smith
[1987]
studied
the
2~
period
solution
of
the
forced-damp
Cuffing's
equation
with
negative
stiffness,
with
linear
damping
proportional
to
the
velocity.
It
has
very
rich
structures.
Many
problems
in
physical
systems
involve
the
nonlinear
interaction
of
two
oscillators
with
different
frequencies.
When
these
frequencies
are
incommensurate,
the
interaction
involves
the
amplitude
rather
than
the
phases
of
each
oscillator.
On
the
other
hand,
when
the
frequencies
are
in
a
ratio
closely
corresponding
to
a
rational
fraction
of
a
small
denominator,
phase
locking
occurs
and
the
dynamics
is
much
richer,
see,
e.g.,
Perez
and
Glass
[1982]
and
Coppersmith
[1987].
Wiesenfeld
and
Satija
[1987]
studied
the
286

effect
of
noise
on
systems
having
two
competing
frequencies.
When
the
system
is
mode-locked,
random
perturbations
are
effectively
suppressed,
while
outside
the
locking
interval
relatively
high
levels
of
broadband
noise
are
presented.
Such
effects
have
also
been
observed
in
mode-locked
lasers.
We
shall
discuss
this
in
the
next
chapter.
Van
Buskirk
and
Jeffries
(1985]
have
observed
chaotic
dynamics
from
the
nonlinear
charge
storage
of
driven
Si
p-n
junction
passive
resonators.
And
the
behavior
is
in
good
agreement
with
theoretical
models.
Yazaki,
Takashima
and
Mizutani
(1987]
investigated
the
Taconis
oscillations,
which
are
spontaneous
oscillations
of
gas
columns
thermally
induced
in
a
tube
with
steep
temperature
gradients.
Near
the
overlapping
region,
the
intersection
of
the
stability
curves
for
two
different
modes
with
incommensurate
frequencies
has
been
found
that
both
modes
can
be
excited
simultaneously
and
competition
between
them
can
lead
to
complex
quasiperiodic
and
chaotic
states.
These
problems
are
of
particular
interest
for
some
technologies,
such
as
phase
locking
of
several
independent
lasers
of
the
same
kind,
called
the
phased
array.
We
shall
come
to
this
in
the
next
chapter.
Knobloch
and
Proctor
(1988]
have
investigated
fully
the
special
case
where
the
frequencies
are
in
the
ratio
of
2:1.
On
the
subject
of
resonance,
Parlitz
and
Lauterborn
(1985]
have
shown
numerically
a
periodic
recurrence
of
a
specific
fine
structure
in
the
bifurcation
set
of
the
Duffing
equation
which
is
closely
related
with
the
nonlinear
resonance
of
the
system.
Gray
and
Roberts
(1988a,b,c,d],
in
a
series
of
papers,
re-examined
chemical
kinetic
models
described
by
two
coupled
ordinary
differential
equations
containing
at
most
three
control
parameters,
originally
studied
by
Sal'nikov
(1949].
They
have
found
some
interesting
effects
and
details
which
have
missed
earlier.
Recently,
Wiesenfeld
and
Hadley
(1989]
have
described
a
novel
feature
of
certain
arrays
of
N
coupled
nonlinear
oscillators.
They
have
found
that
the
number
of
stable
limit
cycles
scales
as
(N-1)!.
In
order
to
accommodate
this
very
large
multiplicity
of
attractors,
the
287

basins
of
attraction
crowd
more
tightly
in
phase
space
with
increasing
N.
Their
simulations
have
shown
that
for
large
enough
N,
even
minute
levels
of
noise
can
cause
the
system
to
hop
freely
among
the
many
coexisting
stable
attractors.
Lorenz
[1963]
presented
an
analysis
of
a
coupled
set
of
three
quadratic
ordinary
differential
equations,
one
in
fluid
velocity
and
two
in
temperature,
for
fluid
convection
in
a
two-dimensional
layer
heated
from
below
to
modeling
atmospherical
dynamics.
The
Lorenz
equations
are:
dxjdt
a(y-
x),
dyjdt
=ax-
y-
xz,
(6.7-1)
dz/dt
=
-Pz
+
xy,
where
(x,y,z)
E R
3
,
a
(the
Prandtl
number),
a
(the
Rayleigh
number),
and
P
(an
aspect
ratio)
are
real
positive
parameters.
For
any
further
detail
of
Lorenz
equations,
see,
e.g.,
Sparrow
[1982],
Guckenheimer
and
Holmes
[1983],
Moon
[1987].
Amazingly,
equations
completely
equivalent
to
the
set
of
Lorenz
equations,
Eq.(6.7-1),
occur
in
laser
physics
explaining
the
phenomenon
of
irregularly
spiking
of
lasers.
For
the
discussion
of
Lorenz
equations
in
laser
physics,
see
for
instance,
Haken
[1983],
Haken
[1975a],
Sparrow
[1986].
For
a
more
comprehensive
review
of
cooperative
phenomena
in
systems
far
from
thermal
equilibrium
including
lasers,
nonlinear
wave
interactions,
tunnel
diodes,
chemical
reactions,
and
fluid
dynamics,
see
Haken
[1975b]
as
well
as
his
book
on
synergetics
[1983].
It
suffices
to
say
that
for
a <
1,
the
origin
(0,0,0)
is
globally
attracting,
i.e.,
the
fluid
is
at
rest
and
with
linear
temperature
gradient
(corresponding
to
no
laser
action
in
lasre
physics).
This
is
because
the
trace
of
the
Jacobian
(the
divergence
of
the
vector
field)
is
equal
to
-(a
+ 1 + p) <
0.
In
fact,
for
a <
1,
the
origin
is
a
hyperbolic
sink
and
is
the
only
attractor.
For
a =
1,
one
of
the
eigenvalues
of
the
linearized
system
is
zero,
and
the
others,~,=
-p,
~
2
=-(a+
1),
thus
a
pitchfork
bifurcation
occurs,
that
is,
the
pure
conductive
solution
becomes
unstable
and
the
convective
motion
starts
(corresponding
to
288

laser
at
threshold
and
lasing
starts).
As
for
a>
1,
the
origin
is
a
saddle
point
with
a
one-dimensional
unstable
manifold,
and
there
is
a
pair
of
nontrivial
steady
solutions
(or
fixed
points
s.
and
S_)
at
(x,y,z)
=
(±P(a-1),
±p(a-1),
a-1),
and
these
are
sinks
for
1
<a<
ah =
a(a
+ p +
3)/(a-
P-
1).
At
a=
aha
Hopf
bifurcation
occurs
at
the
fixed
points,
since
the
eigenvalues
of
the
matrix
of
the
linear
system
are:
~,=-(a+
P +
1),
and
~
2
=
±i2a(a+1)/(a-P-1).
To
allow
imaginary
roots,
here
we
assume
that
a > 1 + p.
Otherwise,
~
2
are
real.
For
a >
ah,
the
nontrivial
fixed
points
are
saddle
points
with
two-dimensional
unstable
manifolds.
Thus,
for
a >
ah,
all
three
fixed
points
are
saddles,
i.e.,
unstable.
Nonetheless,
an
attracting
set
does
exist
and
may
contain
complicated
bounded
solutions.
One
may
think
that
the
Hopf
bifurcation
occurring
as
a
passes
through
ah
will
give
rise
to
stable
periodic
orbits,
but
subsequently
it
has
been
found
that
the
bifurcation
is
subcritical
(Marsden
and
McCracken
1976],
so
that
unstable
periodic
orbits
shrink
down
to
the
sinks
as
a
increases
towards
ah
and
no
closed
orbits
exist
near
these
fixed
points
for
a >
ah.
Thus,
qualitatively
we
can
anticipate
that
all
the
solutions
will
have
the
following
behavior
in
the
phase
space.
For
all
positive
values
of
the
parameters,
all
solutions
of
the
equations
eventually
lie
in
some
bounded
region
and
they
all
tend
towards
some
set
in
three-
dimensional
phase
space
with
zero
volume.
This
follows
from
the
dissipative
nature
of
the
flow,
and
implies
that
solutions
do
not
wander
about
the
whole
three-dimensional
space
but
eventually
come
close
to
point-like,
line-like,
or
sheet-like
objects
in
the
phase
space.
Note
also
that
the
fixed
points
s.
and
s_
will
be
stable
for
a < p +
1,
but
lose
stability
at
some
a
if
a > p +
1.
By
using
an
averaging
procedure,
one
can
show
that
there
is
a
stable
symmetric
periodic
orbit
or
limit
cycle
for
all
large
enough
a
if
3a
>
2P
+
1.
Note
that
the
Lorenz
equations
are
289

symmetric
under
the
mapping
(x,y,z)
~
(-x,-y,z).
Also
notice
that
the
region
3a
> 2P + 1
is
larger
than
and
includes
the
region
of
a > P +
1.
That
is,
whenever
S+
or
s_
lose
stability
at
a
finite
a,
there
is
a
stable
periodic
orbit
at
large
enough
a.
In
the
case
when
3a
> 2P + 1
but
a < p +
1,
it
can
be
shown
that
there
are
two
unstable
periodic
orbits,
i.e.,
a
symmetric
pair
of
non-symmetric
orbits
which
exist
for
all
large
enough
a,
in
addition
to
the
stable
symmetric
orbit.
Various
other
regions
and
other
limits
of
the
equations
can
be
analysed
in
different
ways.
For
instance,
the
limit
a = a
~
~
and
p = 1
has
been
analysed
by
Shimada
and
Nagashima
[1978],
Fowler
and
McGuinness
[1982,
1984].
Again,
the
references
cited
earlier
are
urged
to
consult
with.
If
it
was
not
for
the
complicated
but
beautiful
results
obtained
by
numerically
integrating
the
Lorenz
equations
on
a
computer,
the
Lorenz
equations
would
not
have
received
such
interest
and
attention.
Indeed,
a
computer
is
necessary
to
proceed
much
beyond
the
qualitative
description
earlier.
In
the
following
we
will
give
a few
well-known
figures
just
to
entice
the
reader
for
further
reading.
We
will
fix
two
parameters
a
and
p,
and
let
a
vary.
It
should
be
noted
that
the
values
used
by
Lorenz
and
most
other
researchers
are
a =
10,
p =
8/3,
and
similar
behavior
occurs
for
other
values.
With
these
parameters
fixed,
one
find
ah
=
24.74.
Lorenz
then
fixed
a = 28
and
integrated
Eqs.(6.7-1)
numerically.
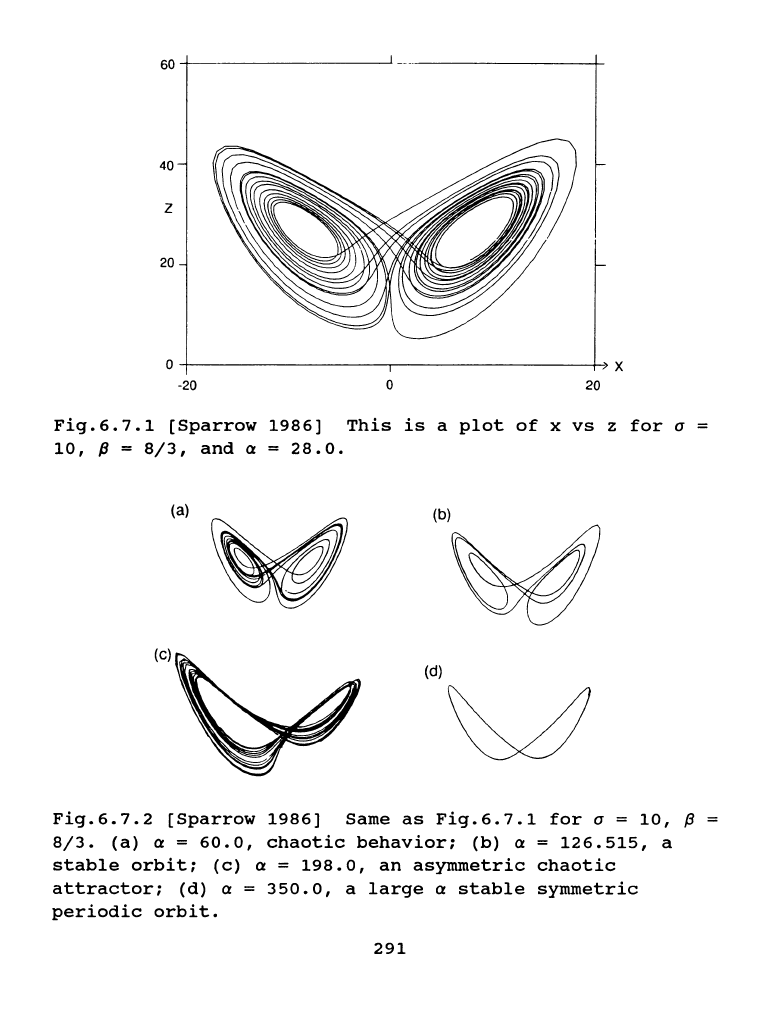
Fig.6.7.1
shows
a
two-dimensional
projection
of
a
typical
orbit
calculated
with
the
above
set
of
parameters.
The
transients
have
been
allowed
to
die
away
before
plotting
begins.
The
orbit
appears
to
oscillate
back
and
forth,
rotating
first
on
one
side
and
then
on
the
other
and
never
closing
up!
Fig.6.7.2
show
numerically
calculated
orbits
at
other
parameter
values.
For
the
same
a
and
p,
(a)
a =
60,
resulted
in
a
chaotic
behavior;
(b)
a =
126.515
resulted
in
a
stable
orbit;
(c)
a = 198
resulted
in
an
asymmetric
chaotic
attractor;
and
(d)
a =
350
resulted
in
a
typical
large-a
stable
symmetric
periodic
orbit.
290
-20 0
20
Fig.6.7.1
[Sparrow
1986)
This
is
a
plot
of
x
vs
z
for
a
10,
p =
8/3,
and
a =
28.0.
(a)
(b)~
(c)
(d)
w
Fig.6.7.2
[Sparrow
1986]
Same
as
Fig.6.7.1
for
a =
10,
p
8/3.
(a)
a =
60.0,
chaotic
behavior;
(b)
a =
126.515,
a
stable
orbit;
(c)
a =
198.0,
an
asymmetric
chaotic
attractor;
(d)
a =
350.0,
a
large
a
stable
symmetric
periodic
orbit.
291

For
any
further
details
on
the
chaotic
behavior
of
the
Lorenz
equations
as
well
as
other
well-known
nonlinear
systems,
see
the
references
cited
earlier.
A
prototype
equation
to
the
Lorenz
model
of
turbulence
contains
just
one
nonlinearity
in
one
variable
has
been
proposed
by
Rossler
[1976]:
dxjdt
=
-(y
+
z),
dyjdt
= x +
0.2y,
dzjdt
=
0.2
+
z(x-
5.7).
(6.7-2)
There
is
only
a
single
nonlinear
term,
and
of
course
there
is
no
longer
any
immediate
physical
interpretation.
Nonetheless,
the
flow
in
phase
space
allows
for
"folded"
diffeomorphisms,
called
horseshoe
maps
[Smale
1967],
are
well-known
in
the
geometric
theory
of
dynamical
systems.
In
fact,
each
of
them
can
give
rise
to
a
three-dimensional
suspension,
and
the
limit
set
is
the
strange
attractor
and
whose
cross-section
is
a
two-dimensional
cantor
set.
The
flow
is
nonperiodic
and
structurally
stable
[Ruelle
and
Takens
1971]
even
though
all
orbits
are
unstable.
Thus,
most
of
the
results
of
the
Lorenz
model
turn
out
to
be
true
for
Eqs.(6.7-2)
also.
The
simplicity
of
Eqs.(6.7-2)
has
the
added
attribute
that
some
other
results
one
would
like
to
obtain
about
the
strange
attractors,
such
as
basin
structure,
behavior
through
bifurcations,
etc.,
can
be
obtained
easier.
Indeed,
Rossler's
results
stimulated
and
helped
a
better
understanding
of
the
Lorenz
equations.
Recently,
Holmes
and
Williams
[1985)
constructed
a
suspension
of
Smale's
horseshoe
diffeomorphism
of
the
two-dimensional
disc
as
a
flow
in
an
orientable
three
dimensional
manifold.
Such
a
suspension
is
natural
in
that
it
occurs
frequently
in
periodically
forced
nonlinear
oscillators
such
as
the
Duffing
equation.
From
the
suspension,
they
constructed
a
know-holder
or
template
in
such
a
way
that
the
periodic
orbits
are
isotopic
to
those
in
the
full
three-dimentional
flow.
Theorems
of
existence,
uniqueness
and
nonexistence
for
families
of
torus
knots,
and
these
families
to
resonant
Hamiltonian
bifurcations
which
occur
as
horseshoes
are
created
in
a
one-parameter
family
of
292

area
preserving
maps.
Saravanan
et
al
[1985)
have
studied
the
effect
of
modulating
the
control
parameter
a
with
a
frequency
n,
i.e.,
in
the
second
equation
of
Eqs.(6.7-1),
replace
a
by
a[1
+
£cos(nt)].
They
have
found
that
this
modulation
is
a
very
sensitive
probe
of
the
limit
cycle
of
frequency
n
0
near
the
Hopf
bifurcation
point.
For
n =
2n
0
,
and
low
amplitudes,
such
modulation
leads
to
a
hastening
of
chaos.
But
for
higher
amplitudes,
the
destabilization
ceases
and
beyond
a
critical
amplitude
the
limit
cycle
of
frequency
n
0
is
stabilized.
The
existence
of
such
a
critical
amplitude
follows
from
a
variant
of
the
perturbation
theory.
They
noted
that
the
possibility
of
stabilizing
the
limit
cycles
is
particularly
interesting
as
it
restores
the
correspondence
with
the
real
hydrodynamics
up
to
the
onset
of
chaos.
The
routes
to
chaos
in
this
modulated
systems
are
of
interest
for
further
study.
Shimizu
and
Morioka
[1978]
have
shown
that
by
changing
variables,
Lorenz
equations
can
be
written
as
a
differential
system
describing
a
particle
in
some
fourth
order
potential
depending
on
a
varying
parameter.
Coullet,
Tresser
and
Arneodo
[1979]
have
shown
that
such
simple
differential
systems
lead
to
the
transition
to
stochasticity.
Andrade
[1982)
used
the
Carleman
embedding
to
obtain
some
results
for
the
Liapunov
exponents
of
the
Lorenz
model.
Birman
and
Williams
[1983a,b)
in
a
series
of
papers
have
asked
the
questions
such
as
can
the
periodic
orbits
of
a
dynamical
system
on
s
3
or
R
3
be
knotted,
and
if
so,
what
kinds
of
knots
can
occur,
and
what
are
the
implications?
Franks
and
Williams
[1984]
have
further
shown
that
with
positive
topological
entropy,
there
are
infinitely
many
distinct
knot
types.
Results
are
obtained
for
the
Lorenz
model.
Williams
[1983]
proved
that
Lorenz
knots
are
prime.
Holmes
and
Williams
[1985)
have
constructed
an
suspension
of
Smale's
horseshoe
diffeomorphism
(we
have
not
discussed
this
topic
due
to
its
complicated
construction,
we
refer
the
reader
to
Smale
[1967],
Irwin
[1980],
Guckenheimer
and
Holmes
[1983))
293
