Lee K.K. Lectures on Dynamical Systems, Structural Stability and Their Applications
Подождите немного. Документ загружается.


with
this
issue
as
food
for
thought.
&.a A
new
definition
of
stability
As
we
have
discussed
earlier,
there
are
several
notions
of
stability,
and
structural
stability
is
intuitively
easy
to
understand
and
has
some
nice
attributes.
Yet
we
have
also
noted
that
structural
stability
is
in
some
sense
a
failure
because
structurally
stable
systems
are
not
dense
for
dimensions
~
3.
It
is
true
that
Anosov
systems,
AS
systems,
and
Morse-Smale
systems
(or
hyperbolic
strange
attractors)
are
structurally
stable,
but
they
are
rather
special,
and
most
strange
attractors
and
chaotic
systems
which
appear
in
applications
(such
as
the
Lorenz
model)
are
not
structurally
stable.
We
have
also
pointed
out
that
there
have
been
several
attempts
to
define
stability
such
that
the
stable
systems
are
dense,
but
they
have
failed.
Recently,
Zeeman
[1988]
proposed
a new
definition
of
stability
for
dynamical
systems
which
is
particularly
aimed
at
nonlinear
dissipative
systems.
There
are
several
advantages
of
this
new
definition
of
stability
than
that
of
structural
stability.
For
instance,
the
stable
systems
(in
this
new
definition)
are
dense,
therefore
most
strange
attractors
are
stable,
including
non-hyperbolic
ones.
This
approach
offers
an
alternative
to
structural
stability.
As
we
shall
see,
to
a
certain
extent,
it
is
a
complement
to
structural
stability.
In
the
following,
we
shall
briefly
discuss
Zeeman's
stability
(for
simplicity,
we
shall
simply
call
it
stability),
its
advantages
over
and
its
differences
from
structural
stability,
some
examples,
and
some
difficulties.
To
limit
our
discussion,
we
shall
only
discuss
the
stability
of
vector
field
and
flows,
we
shall
leave
the
diffeomorphism&
for
the
readers
to
read
the
paper
by
Zeeman.
Let
M
be
a
smooth
oriented
n-dimensional
Riemannian
manifold.
Let
R+
denotes
the
non-negative
reals.
Given a
smooth
vector
field
v
on
M,
and
given
£ > o,
the
314

Fokker-Planck
equation
for
v
with
£-diffusion
is
the
partial
differential
equation
on
M
ut
=
£Uxx
-
div(uv),
(6.8-1)
where
u:
MxR.
~
R.,
u(x,t)
~
o,
x £
M,
t
~
0
and
the
integral
of
u
over
M
equals
to
unity.
Here
uxx
is
the
Laplacian
of
u,
and
the
divergence
are
determined
by
the
Riemannian
structrue
(see
Section
2.4).
The
function
u
represents
the
smooth
probability
density
of
a
population
on
M
driven
by
v
and
subject
to
£-small
perturbation.
For
further
details
on
Fokker-Planck
equation,
see
any
probability
theory
or
statistical
mechanics
books,
see
also
Risken
[1984].
Let
uv,c: M
~
R+
denote
the
steady-state
solution
of
Eq.(6.8-1).
If
M
is
compact
(for
noncompact
M a
suitable
boundary
condition
on
v
will
be
required
for
the
existence
of
u),
it
has
been
established
for
the
existence,
uniqueness,
and
smoothness
of
the
steady-state
solution
of
Eq.(6.8-1).
As
before,
next
we
shall
define
the
equivalence
relations.
Two
smooth
functions
u,
u•:
M
~
R
are
said
to
be
equivalent,
u-
u•,
if
there
exist
diffeomorphisms
a,
p
of
M
and
R
such
that
the
following
diagram
commutes:
M u
~
R
a
~
M
~
p
u•_..
R.
We
say
a
function
is
stable
if
it
has
a
neighborhood
of
equivalents
in
the
space
of
all
smooth
functions
on
M
with
c-
topology.
We
define
two
smooth
vector
fields
v,
v•
on
M
to
be
£-
equivalent
if
uv,c - uv'
,c.
A
vector
field
is
said
to
be
£-stable
if
it
has
a
neighborhood
of
£-equivalents
in
the
space
X(M)
of
all
smooth
vector
fields
on
M
with
c-
topology.
A
vector
field
is
stable
if
it
is
£-stable
for
arbitrarily
small
£ >
o.
Zeeman
[1988]
has
shown
that
£-stable
vector
fields
are
open
and
dense,
and
stable
vector
fields
are
dense
(but
not
necessarily
open).
As
an
example,
let
M =
R,
v(x)
=
-x.
Then
the
315

Fokker-Planck
equation
becomes
ut
=
euxx
+ (ux>x·
Then
we
can
solve
the
steady-
state
equation
directly
and
we
obtain
u = (AJ
eY'
12
'dy
+
B)
e·x'/
2
•
where
A
and
B
are
constants.
If
A < 0
then
the
bracket
tends
to
~
as
x
~
~.
and
so
u < 0
for
sufficiently
large
values
of
x.
And
if
A > 0
then
u < 0
for
sufficiently
large
negative
values
of
x.
Therefore,
u
~
0
implies
A = o. And
the
condition
of
unit
probability
determines
the
value
of
B,
and
we
have
u = e·x'
12
'/21fE.
Clearly,
the
steady-state
solution
is
just
the
normal
distribution.
Intuitively
we
can
see
that
if
there
were
no
diffusion
(e
=
0),
then
the
whole
population
would
be
driven
towards
the
origin,
approaching
the
Dirac
delta
function
as
t
~
~.
When
e > o,
the
diffusion
term
pushes
the
population
away
from
the
origin,
opposing
the
incoming
drive
term
until
they
reached
a
balance
in
the
normal
distribution.
Since
the
circle
is
the
simplest
nontrivial
compact
manifold,
let
us
look
at
some
examples
of
vector
fields
on
s
1
•
Here
we
shall
not
get
into
the
detailed
construction
of
the
probability
density
u(x),
but
we
shall
consider
some
special
cases
qualitatively.
Let
v
be
a
vector
field
on
s
1
given
by
v:
s
1
~
R.
If
v >
0
the
flow
of
v
is
a
cycle.
The
invariant
measure
of
the
flow
is
kjv,
where
k
is
a
constant,
chosen
in
such
a way
that
kjv
=
1.
Furthermore,
if
v
has
only
two
critical
points,
a minimum
at
p
and
a maximum
at
q.
In
the
situation
of
the
pendulum,
p
is
the
position
where
the
pendulum
stands
vertically
upward
and
nearly
at
rest
(highest
potential
energy
but
lowest
kinetic
energy),
and
q
is
the
position
where
the
pendulum
hangs
vertically
downward
with
maximum
velocity
(lowest
potential
energy
but
highest
kinetic
energy).
Then
the
invariant
measure
will
have
a maximum
at
p
where
the
flow
lingers
longest
and
a minimum
at
q
where
the
flow
is
the
most
rapid
as
shown
in
Fig.6.8.1(a).
The
steady
state
of
the
Fokker-Planck
equation
is
an
e-approximation
of
the
measure
and
qualitatively
the
same,
with
maximum
and
minimum
occurring
slightly
before
the
flow
reaches
p
and
q
316

respectively.
We
have
discussed
this
in
Ch.1
in
detail.
max
max
u
0
u
u(q)
n
p
~
C)
~~
q
(a)
(b)
Fig.6.8.1
(Zeeman
1988]
Now
consider
the
case
where
v
has
an
attractor
at
p
and
a
repeller
at
q,
as
shown
in
Fig.6.8.1(b).
The
invariant
measure
is
the
delta
function
at
p,
and
the
steady-state
of
the
Fokker-Planck
equation
will
resemble
a
normal
distribution
near
p.
If
v
is
a
gradient
field,
then
the
maximum
and
minimum
will
be
at
p
and
q,
but
if
v
is
non-gradient,
then
the
maximum
will
be
near
p
but
the
minimum
may
not
be
anywhere
near
q.
Note
that
the
two
steady-states
shown
in
Fig.6.8.1
are
qualitatively
similar,
and
by
the
(new)
definition
of
equivalence,
they
are
equivalent.
And
indeed,
they
are
€-
equivalent.
It
is
then
nature
to
ask:
if
we
take
a
parametrized
family
of
vector
fields
going
from
one
to
the
other,
are
all
the
members
of
this
family
equivalent?
If
so,
does
this
mean
that
the
resulting
bifurcation
must
be
stable?
Surprisingly,
both
answers
are
affirmative.
Fig.6.8.2
shows
two
fold
bifurcations,
in
each
case
a
sink
(attractor)
coalesces
with
a
source
(repeller)
r
at
a
fold
point
f
and
disappears
(see
Section
6.3).
Note
that,
317

suppose
one
of
the
zeros
p
is
non-hyperbolic,
then
a
c--small
perturbation
of
the
vector
field
near
p
can
alter
p
to
a
source
or
to
a
sink.
But
since
we
leave
all
the
other
original
zeros
of
v
unaltered,
we
have
changed
the
number
of
sources
in
either
case.
That
was
the
reason
behind
Theorem
6.3.1.
Thus,
this
type
of
system
is
not
structurally
stable.
Zeeman
[1988]
gives
a
slightly
different
argument.
Fig.6.8.2
[Zeeman
1988]
It
appears
that
any
two
limit
cycles
in
the
plane
are
e-
equivalent.
In
fact,
the
flows
on
any
two
limit
cycles
are
topologically
equivalent.
The
following
example
will
illustrate
that
two
limit
cycles
in
the
plane
may
not
be
e-equivalent.
Fig.6.8.3(a)
shows
a
limit
cycle
on
which
the
flow
is
as
in
Fig.6.8.1(a),
with
a
source
inside.
This
situation
would
arise
from
the
following
dynamical
equations
in
polar
coordinates
[Zeeman
1981]:
dr/dt
=
r(1-
r),
d9/dt
=
2-
rcose.
The
resulting
steady-state
resembles
a
volcano
crater,
with
the
rim
of
the
crater
above
the
limit
cycle,
with
a maximum
at
p
and
a
saddle
at
q
on
the
lip
of
the
crater
and
a
minimum
at
the
source.
Let
us
compare
this
with
the
hysteresis
cycle
on
a
cusp
catastrophe
given
by
the
equations
in
Cartesian
coordinates:
dx/dt
=
-y/k,
dy/dt
=
k(x
+
Y-
Y
3
),
where
k >> o.
This
is
the
same
as
the
van
der
Pol
oscillator
with
large
damping:
d
2
X/dt
2
+
k(3X
2
-
1)dxjdt
+ x =
o.
Here
the
limit
cycle
has
two
branches
of
slow
manifold
separated
by
the
catastrophic
jumps
between
the
two
branches
318
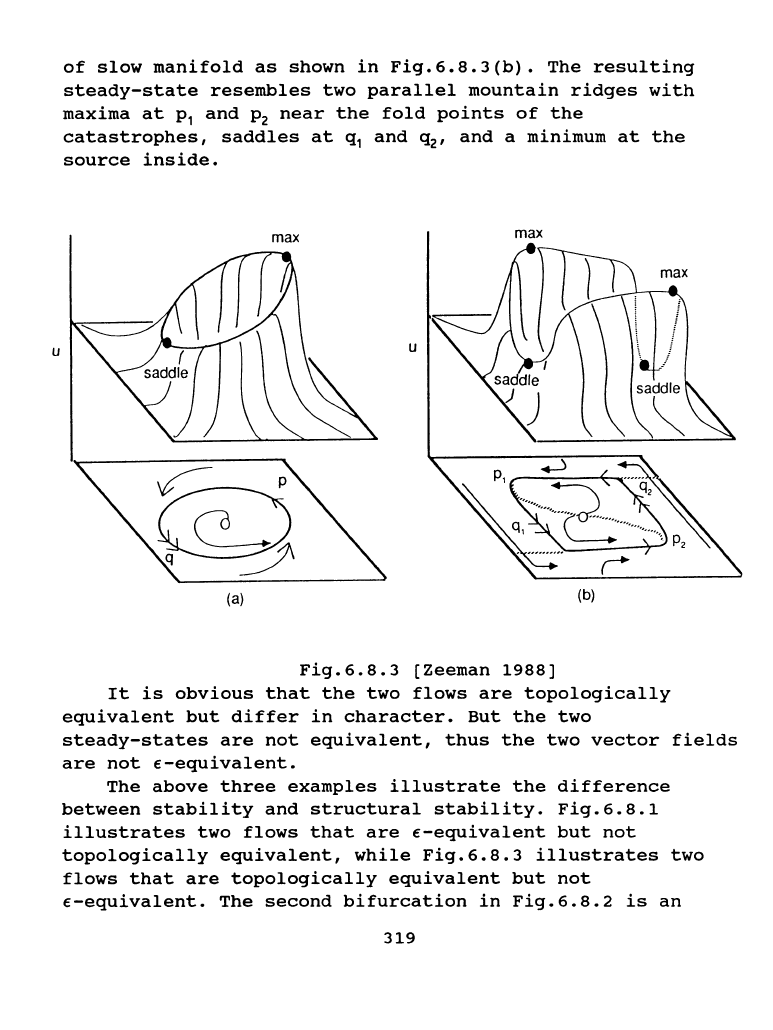
u
of
slow
manifold
as
shown
in
Fig.6.8.3(b).
The
resulting
steady-state
resembles
two
parallel
mountain
ridges
with
maxima
at
p
1
and
p
2
near
the
fold
points
of
the
catastrophes,
saddles
at
q
1
and
~·
and
a
minimum
at
the
source
inside.
max
max
u
(a)
(b)
Fig.6.8.3
[Zeeman
1988]
It
is
obvious
that
the
two
flows
are
topologically
equivalent
but
differ
in
character.
But
the
two
steady-states
are
not
equivalent,
thus
the
two
vector
fields
are
not
£-equivalent.
The
above
three
examples
illustrate
the
difference
between
stability
and
structural
stability.
Fig.6.8.1
illustrates
two
flows
that
are
£-equivalent
but
not
topologically
equivalent,
while
Fig.6.8.3
illustrates
two
flows
that
are
topologically
equivalent
but
not
£-equivalent.
The
second
bifurcation
in
Fig.6.8.2
is
an
319

example
of
a
flow
that
is
stable
but
not
structurally
stable.
Conversely,
in
a
one-parameter
family
of
flows
JO~n~ng
those
in
Fig.6.8.3,
there
will
be
a
bifurcation
where
the
flow
is
structurally
stable
but
not
stable.
Roughly
speaking,
structural
stability
captures
the
topological
properties
of
the
system
like
basins
of
attraction,
separatrices
and
saddle
connections,
while
Zeeman's
stability
criteria
captures
qualitative
properties
of
the
measure.
Putting
it
differently,
structural
stability
retains
the
orbit
structure
but
ignores
the
speed
of
flow
and
the
smoothness,
and
loses
touch
with
the
experimental
data,
while
Zeeman's
stability
retains
the
smoothness
and
keeps
in
touch
with
the
data
but
ignores
the
dynamics
and
the
direction
of
flow.
In
this
sense,
we
say
that
they
complement
each
other.
As
we
have
mentioned
earlier,
structurally
stable
systems
are
not
dense
for
dimensions
~
3
in
general,
while
Zeeman's
stable
systems
are
dense.
Thus
the
qualitative
properties
of
Zeeman's
stable
models
are
robust,
i.e.,
they
are
preserved
under
perturbations.
Although
the
phenomenon
may
be
a
perturbation
of
the
model,
the
robustness
of
the
model
will
remain
to
be
a
valid
description
of
the
phenomenon.
Another
serious
criticism
of
structural
stability
is
its
lack
of
smoothness.
As
we
have
noticed
before,
in
its
definition,
it
is
necessary
that
the
equivalence
relation
be
a
homeomorphism
(for
topological
conjugacy
and
equivalence,
see,
Section
4.2)
rather
than
a
diffeomorphism.
For
example,
Fig.4.1.1(a)
is
topologically
equivalent
to
it
with
a
rotation
so
that
it
spirals
out.
Clearly
the
equivalence
is
only
subject
to
homeomorphism
but
not
diffeomorphism.
The
importance
of
smooth
equivalence
relations
is
that
if
we
can
prove
a
given
situation
is
smoothly
equivalent
to
a
standard
model,
then
all
the
smooth
qualitative
properties
of
the
standard
model
are
automatically
carried
over
to
the
given
situation.
But
if
a
given
situation
is
only
topologically
equivalent
to
a
standard
model,
then
any
smooth
qualitative
320

properties
of
the
given
situation
has
to
be
stated
and
proved
separately.
It
should
be
noted
that
Zeeman's
stability
can
not
distinguish
between
volume-preserving
flows.
This
is
because
the
theory
is
designed
for
dissipative
systems,
and
is
not
suitable
for
Hamiltonian
systems.
But
nor
is
structural
stability
useful
to
study
Hamiltonian
systems
because
all
Hamiltonian
systems
are
structurally
unstable.
Section
4
of
Zeeman's
paper
develops
an
analogous
theory
for
the
stability
of
diffeomorphisms.
It
has
been
pointed
out
that
this
theory
is
not
as
elegant
as
that
for
flows.
The
next
two
sections
of
Zeeman's
paper
prove
the
existence,
uniqueness,
and
classification
theorems.
It
is
clear
that
these
results
are
the
beginning
of
a
very
interesting
and
fruitful
undertaking.
At
the
end
of
the
paper,
Zeeman
suggested
some
open
questions
for
further
research:
(a)
Extend
the
results
for
flows
to
non-compcat
manifolds
with
suitable
boundary
conditions;
(b)
Prove
the
analogous
density
and
classification
theorems
for
diffeomorphisms;
(c)
Develop
a
theory
of
unfoldings
of
unstable
vector
fields
of
finite
codimensions;
(d)
Investigate
the
stability
of
specific
strange
attractors,
both
Axiom
A
and
non-Axiom
A,
such
as
Lorenz
and
Henon;
(e)
Extend
the
results
from
c~
to
cr, r f
[l,oo).
In
these
broad
classes
of
problems,
the
last
two
classes
are
of
immediate
impact
on
applications.
Indeed,
some
strange
attractors,
such
as
Lorenz,
Cantor-like,
Henon,
van
der
Pol,
Duffing,
coupled-attractors,
etc.
must
be
studied
with
Zeeman's
criteria
for
stability
and
classification.
Of
course,
with
better
understanding
of
this
stability
criteria,
a
even
more
general
and
more
satisfying
definition
of
stability
may
evolve.
Examples
and
practical
problems
may
provide
enough
imputus
for
mathematicians
to
construct
such
more
satisfying
criteria
for
stability.
321

Appendix
In
this
appendix,
we
shall
use
the
Lorenz
model
to
illustrate
the
center
manifold
theorem
and
its
applications
for
bifurcation
calculations.
For
more
detail,
see,
e.g.,
Guckenheimer
and
Holmes
[1983],
Carr
[1981].
We
shall
study
the
bifurcation
of
the
Lorenz
equation,
Eq.6.7.1,
occurring
at
the
origin
and
a =
1.
The
Jacobian
ma[r~;
at
~:· o~:qr~
is
When a =
1,
this
matrix
has
eigenvalues
o,
-a
-
1,
and
-p
with
eigenvectors
(1,
1,
0),
(a,
-1,
0),
and
(0,
o,
1).
By
using
the
eigenvectors
as
a
basis
for
a new
coordinate
system,
we
have
[
1/
(1
+
a)
1/
(1
+
a)
0
aj(1
+
a)
-1/
(1
+
a)
0
Then
the
Lorenz
equation
becomes
dujdt
-a(u
+
av)w/(1
+a),
dvjdt
=
-(1
+
a)v
+
(u
+
av)w/(1
+a),
dwjdt
=
-pw
+
(u
+
av)
(u-
v),
(A-1)
and
in
matrix
form
we
have
[
du/dtl
dvjdt
dwjdt
0
-(l+a)
0
[
-a(u
(u
+
(u
+
+
av)w/(1
+
a)]
av)w/(1
+
a)
av)
(u
-
v)
.
Now
the
linear
part
is
in
standard
form.
In
the
new
coordinates,
the
center
manifold
is
a
curve
tangent
to
the
u-axis.
The
projection
of
the
system
onto
the
u-axis
yields
dujdt
= o.
Nonetheless,
the
u-axis
is
not
invariant
because
the
equation
for
dwjdt
contains
u•
term.
If
we
make a
nonlinear
coordinate
transformation
by
setting
w' = w -
322

u•;p,
we
have
dw'jdt
= -pw• + (a -
l)uv
- av•
+
2au(u
+
av)(w'
+ U
2
/P)/(P(l
+a)).
Thus,
in
the
new
coordinate
system
(u,
v,
w'),
we
have
dujdt
=
-a(u
+
av)
(w' +
u•jP)/(1
+a).
Now
the
projection
of
the
system
onto
the
u-axis
in
the
new
coordinate
system
gives
du/dt
=
(-a/P(l
+
a))u
3
•
Note
also
that
there
is
no
u•
term
in
any
of
the
equations
for
v
and
w•.
Thus,
the
u-axis
in
the
new
coordinate
system
is
invariant
up
to
second
order.
Further
efforts
to
find
the
center
manifold
can
proceed
by
additional
coordinate
transformations
which
serve
to
make
the
u-
axis
invariant
for
the
flow
iteratively
by
changes
in
v
and
w•.
323
