Lee K.K. Lectures on Dynamical Systems, Structural Stability and Their Applications
Подождите немного. Документ загружается.


theory
also
has
a
strong
appeal,
for
it
is
one
of
the
main
areas
of
inter-disciplinary
studies
between
pure
mathematics
and
applied
science.
If
we
are
studying
processes
that
evolve
with
time
and
we
wish
to
model
them
mathematically,
then
the
possible
states
of
the
systems
in
which
the
processes
are
taking
place
may
often
be
represented
by
points
of
differentiable
manifolds
known
as
state
spaces
of
the
models.
For
instance,
if
the
system
is
a
single
particle
constrained
to
move
on
a
plane,
then
the
state
space
is
the
Euclidean
R
4
and
the
point
(x
1
,x
2
,v
1
,v
2
)
represents
the
position
of
the
particle
at
x =
(x
1
,x
2
)
with
the
velocity
v =
(v
1
,v
2
).
Note
that
the
state
space
of
a
model
can
be
finite
dimensional,
as
in
the
above
example,
or
it
may
be
infinite
dimensional,
such
as
in
fluid
dynamics.
Furthermore,
it
may
occur
that
all
past
and
future
states
of
the
system
are
completely
determined
by
the
equations
governing
the
system
and
its
state
at
any
one
particular
instance.
In
such
a
case,
the
system
is
said
to
be
deterministic,
such
as
in
Newtonian
mechanics.
The
systems
modeled
in
quantum
mechanics
are
not.
In
the
context
of
deterministic
processes,
usually
they
are
governed
by
a
smooth
vector
field
on
the
state
space.
In
classical
mechanics,
the
vector
field
is
just
another
way
of
describing
the
system.
When
we
say
a
vector
field
governing
a
process
we mean
that
as
the
process
develops
with
time
the
point
representing
the
state
of
the
system
moves
along
a
curve
(integral
curve)
in
the
state
space.
The
velocity
at
any
position
x
on
the
curve
is
a
tangent
vector
to
the
state
space
based
at
x.
We
say
the
process
is
governed
by
the
vector
field,
if
this
tangent
vector
is
the
value
of
the
vector
field
at
x,
for
all
x
on
the
curve.
In
the
qualitative
theory
(or
geometric
theory)
of
differential
equations,
we
study
the
smooth
vector
fields
on
differentiable
manifolds,
focusing
on
the
collection
of
parameterized
curves
on
the
manifold
which
have
the
vector
fields
as
the
tangents
of
the
curves
(integral
curves).
Hopefully,
a
geometric
feature
of
the
curves
and
vector
4

fields
will
correspond
to
a
significant
physical
phenomenon
and
also
is
part
of
a
good
mathematical
model
for
such
a
physical
situation.
In
the
following
we
shall
provide
some
simple
examples
of
qualitative
theory
of
differential
equations
and
illustrate
the
approaches
we
will
be
taking
later.
Let
us
first
examine
some
familiar
examples
in
classical
mechanics
from
a
geometrical
viewpoint.
First,
let
us
consider
a
pendulum
which
is
the
simplest
and
the
most
well-known
dynamical
system.
For
simplicity,
let
us
scale
the
mass
m
and
the
length
1
of
the
pendulum
to
be
unity,
i.e.,
m = 1 =
1.
We
shall
not
dwell
here
on
the
physical
basis
of
the
equation
of
motion
for
the
pendulum,
which
is
d
2
0/dt
2
=-
gsinO
except
that
there
is
no
air
resistance
and
no
friction
at
the
pivot.
By
using
the
definition
of
the
angular
velocity
~
=
dO/dt,
we
can
replace
the
equation
of
motion
by
a
pair
of
first
order
differential
equations:
dO/dt
=
~.
d~/dt
= - g
sinO
(1.1-1)
The
solution
of
Eq.(1.1-1)
is
an
integral
curve
in
the
(0,~)
plane
parameterized
by
t,
and
the
parametrized
coordinates
of
the
curve
are
(O(t),~(t)).
The
tangent
vector
to
the
curve
at
tis
(~(t),
-g
sinO(t)).
From
various
initial
values
of
0
and
~
at
t =
o,
one
obtains
corresponding
integral
curves
and
these
curves
form
the
phase-portrait
of
the
system.
It
can
be
shown
that
the
phase-portrait
of
the
pendulum
looks
like
Fig.1-1a,b.
One
can
easily
distinguish
five
distinct
types
of
integral
curves.
They
can
be
interpreted
as
follows:
(a)
the
pendulum
hangs
vertically
downward
and
is
at
rest,
(b)
the
pendulum
swings
between
two
positions
of
instantaneous
rest
which
are
equally
inclined
to
the
vertical,
(c)
the
pendulum
continuously
rotates
in
the
same
direction
and
never
at
rest,
(d)
the
pendulum
stands
vertically
upward
and
is
at
rest,
5
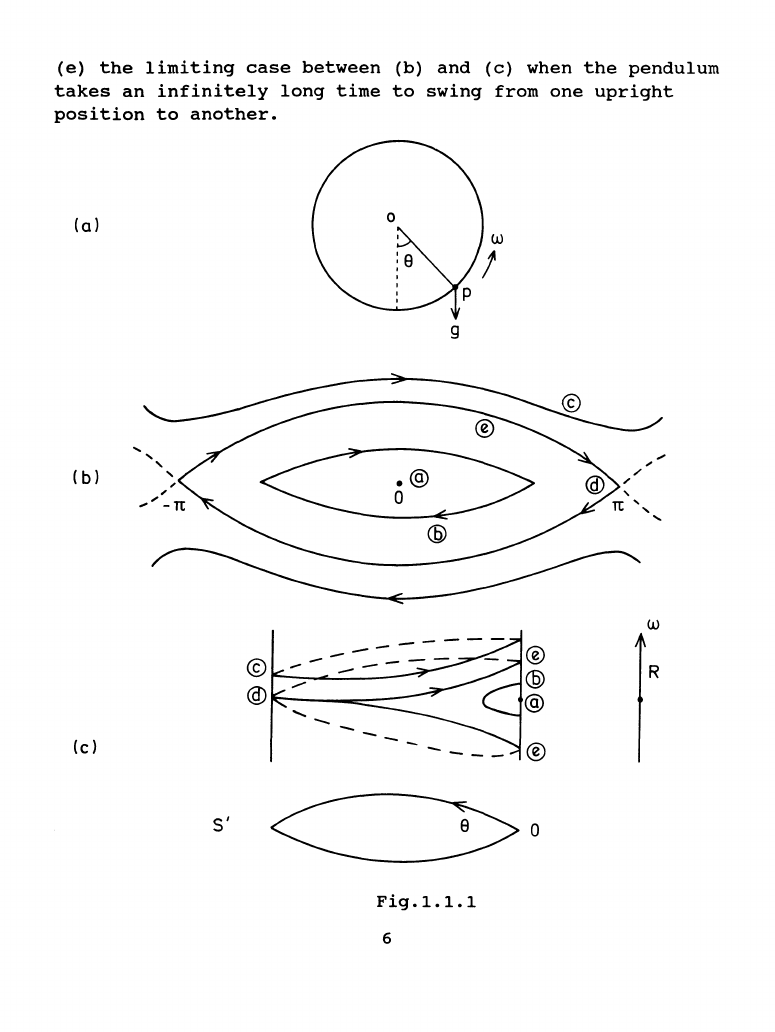
(e)
the
limiting
case
between
(b)
and
(c)
when
the
pendulum
takes
an
infinitely
long
time
to
swing
from
one
upright
position
to
another.
(a)
g
(b)
w
©r-~.......::...----r
R
®~-""""""===----'
(c)
S'
0
Fig.l.l.l
6

There
are
certain
features
in
the
phase-portrait
which
are
unsatisfactory.
First
of
all,
the
pendulum
has
only
two
equilibrium
positions,
the
one
which
hangs
downward
is
stable
and
the
other
which
stands
upward
is
unstable.
Secondly,
solutions
of
type
(c)
are
periodic
motions
of
the
pendulum
but
it
appears
as
nonperiodic
curves
in
this
particular
form
of
phase-portrait.
In
fact,
we
ought
to
regard
e = eo
and
e =
2n~
+
eo
for
any
given
integer
n
as
giving
the
same
position
of
the
pendulum.
In
other
words,
the
configuration
space,
which
is
the
differentiable
manifold
representing
the
spatial
positions,
of
a
pendulum
is
really
a
circle
rather
than
a
straight
line.
Thus,
we
should
replace
the
first
factor
R
of
R
2
by
the
circle
s
1
,
which
is
the
real
module
2~.
By
keeping
e
and
as
two
parameters,
we
obtain
the
phase-portrait
on
the
cylinder
s
1
xR
as
shown
in
Fig.1.1c.
Consider
the
kinetic
energy
T
and
the
potential
energy
V
of
the
pendulum,
and
T =
1/2~
2
and
V
g(1-
cose).
Let
the
total
energy
of
the
pendulum
be
E = T + v.
Then
it
is
clear
from
Eq.(1.1-1)
that
dE/dt
= o,
i.e.,
Eisa
constant
on
any
integral
curve.
Any
system
with
constant
total
energy
is
called
a
conservative
or
Hamiltonian
system.
In
fact,
for
a
pendulum,
one
can
easily
construct
the
phase-
portrait
by
determining
the
energy
levels
(i.e.,
energy
contours).
One
can
represent
the
state
space
cylinder
s
1
x R
as
a
bent
tube
and
interpret
the
height
as
energy.
This
is
illustrated
in
Fig.1.1.2a.
The
two
arms
of
the
tube
represent
solutions
of
the
same
energy
E >
2g,
where
2g
is
the
potential
energy
of
the
unstable
equilibrium,
with
the
pendulum
rotating
in
the
opposite
direction.
The
stability
properties
of
individual
solutions
are
particularly
apparent
from
the
above
picture.
Any
integral
curve
through
a
point
close
to
the
stable
equilibrium
position
A
remains
close
to
A
at
all
times,
since
the
energy
function
E
attains
its
absolute
minimum
at
A
and
is
stationary
at
B.
In
fact,
B
is
a
saddle
point.
Thus,
there
are
points
arbitrarily
close
to
the
unstable
equilibrium
7
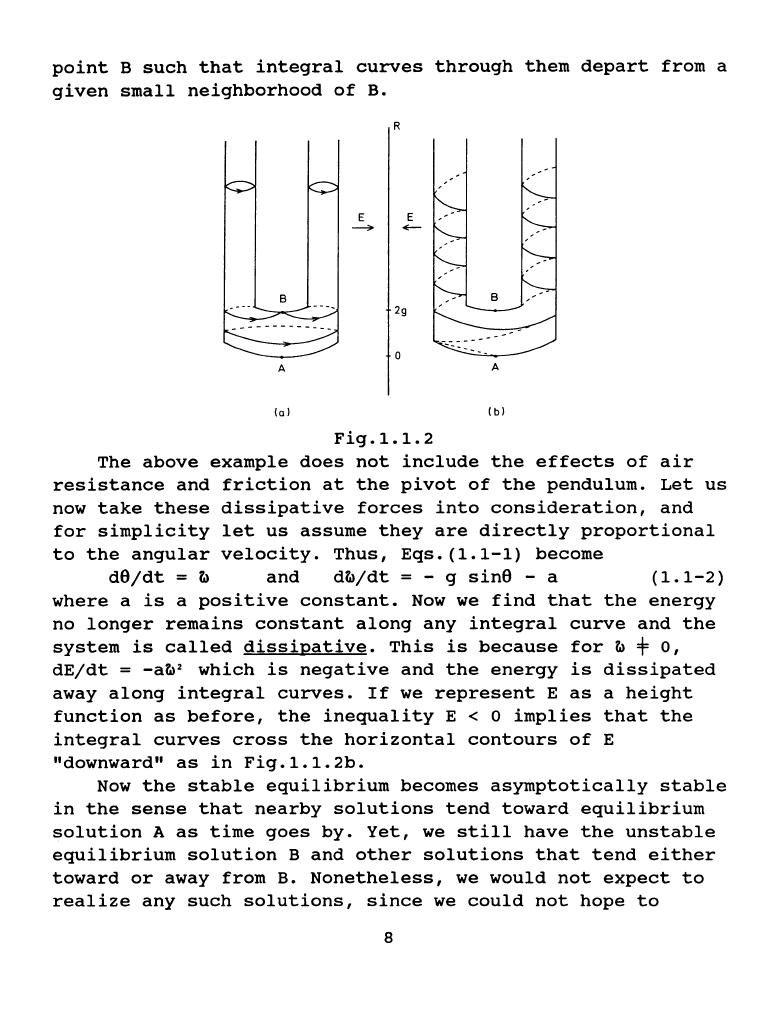
point
B
such
that
integral
curves
through
them
depart
from
a
given
small
neighborhood
of
B.
R
--
E E
____.,
-
B
2g
A
A
(a}
(b)
Fig.l.l.2
The
above
example
does
not
include
the
effects
of
air
resistance
and
friction
at
the
pivot
of
the
pendulum.
Let
us
now
take
these
dissipative
forces
into
consideration,
and
for
simplicity
let
us
assume
they
are
directly
proportional
to
the
angular
velocity.
Thus,
Eqs.(1.1-1)
become
d9jdt
=
~
and
d~/dt
= - g
sin9
- a
(1.1-2)
where
a
is
a
positive
constant.
Now
we
find
that
the
energy
no
longer
remains
constant
along
any
integral
curve
and
the
system
is
called
dissipative.
This
is
because
for
~
+
O,
dE/dt
=
-a~•
which
is
negative
and
the
energy
is
dissipated
away
along
integral
curves.
If
we
represent
E
as
a
height
function
as
before,
the
inequality
E < 0
implies
that
the
integral
curves
cross
the
horizontal
contours
of
E
"downward"
as
in
Fig.l.1.2b.
Now
the
stable
equilibrium
becomes
asymptotically
stable
in
the
sense
that
nearby
solutions
tend
toward
equilibrium
solution
A
as
time
goes
by.
Yet,
we
still
have
the
unstable
equilibrium
solution
B
and
other
solutions
that
tend
either
toward
or
away
from
B.
Nonetheless,
we
would
not
expect
to
realize
any
such
solutions,
since
we
could
not
hope
to
8

satisfy
the
precise
initial
conditions
needed.
By
comparing
the
systems
of
Eqs.(1.1-1)
and
(1.1-2),
one
obtains
some
hint
of
what
is
involved
in
the
important
notion
of
structural
stability.
Roughly
speaking,
a
system
is
structurally
stable
if
the
phase-portrait
remains
qualitatively
(or
topologically)
the
same
when
the
system
is
modified
by
any
sufficiently
small
perturbation.
By
qualitatively
(or
topologically)
the
same,
we
mean
that
some
homeomorphism
of
the
state
space
map
integral
curves
of
the
one
onto
integral
curves
of
the
other.
The
existence
of
systems
(1.1-2)
shows
that
the
original
system
(1.1-1)
is
not
structurally
stable
since
the
constant
a
can
be
as
small
as
we
want.
Yet,
the
systems
(1.1-2)
are
themselves
structurally
stable.
To
distinguish
between
the
systems
(1.1-1)
and
(1.1-2),
we
observe
that
most
solutions
of
the
former
are
periodic
whereas
the
only
periodic
solutions
of
the
latter
are
the
equilibria
[We
shall
discuss
this
in
Chapter
6].
In
fact,
this
last
property
holds
true
for
any
dissipative
system,
since
E
is
decreasing
along
integral
curves.
In
the
above
example,
it
is
more
convenient
and
desirable
to
use
a
state
space
other
than
Euclidean
space,
but
it
is
not
essential.
In
studying
more
complicated
systems,
the
need
for
non-Euclidean
state
spaces
becomes
more
apparent.
Indeed,
it
is
often
impossible
to
study
complicated
systems
globally
using
only
Euclidean
state
spaces.
We
need
non-Euclidean
spaces
on
which
systems
of
differential
equations
are
defined
globally,
and
this
is
one
of
the
reasons
for
studying
differentiable
manifolds.
We
shall
give
a
brief
outline
of
it
in
the
next
chapter.
To
illustrate
the
necessity
of
a
non-Euclidean
state
space
globally,
let
us
consider
the
spherical
pendulum.
We
get
the
spherical
pendulum
from
the
pendulum
by
removing
the
restriction
that
the
rod
moves
in
a
plane
through
the
pivot.
Thus
the
pendulum
is
constrained
to
move
on
a
unit
2-sphere
of
radius
one
in
Euclidean
3-space.
Here
once
again
we
assume
that
the
length
of
the
rod
is
unity.
The
2-sphere
can
9

be
represented
parametrically
by
Euler
angles
e
and
~.
The
equations
of
motion
for
the
spherical
pendulum
are:
d•e;dt•
=sine
cose(d~/dt)•
+ g
sine
(1.1-3)
d
2
~/dt•
=
-2(cote)
dejdt
d~/dt.
We
can
replace
this
system
of
second
order
equations
by
the
equivalent
system
of
four
first
order
equations.
de/dt
&,
d~/dt
~.
(1.1-4)
d&/dt
~·sine
cose
+ g
sine
d~/dt
-
2&~
cote.
The
state
of
the
system
is
determined
by
the
position
of
the
pendulum
on
the
sphere,
together
with
the
velocity
which
is
specified
by
a
point
in
the
2-dim
tangent
plane
of
s•
at
the
position
of
the
pendulum.
In
fact,
the
state
space
is
not
homeomorphic
to
R
4
,
nor
to
s•xR•,
but
is
the
tangent
bundle
of
s•
,
TS
2
•
This
is
the
set
of
all
planes
tangent
to
s•
and
it
is
an
example
of
a
non-trivial
vector
bundle.
We
shall
discuss
these
concepts
in
the
next
chapter.
Locally,
TS'
is
topologically
indistinguishable
from
R
4
and
one
can
use
the
four
variables
e,
~'
&,
~
as
local
coordinates
in
TS'
except
at
the
north
and
south
poles
of
s•
•
The
total
energy
of
the
system
in
terms
of
local
coordinates
is
E =
(&
2
+
~·sine)/2
+
g(1+
cose)
and
it
is
straightforward
to
show
that
E = 0
along
integral
curves,
i.e.,
the
system
is
conservative.
Thus,
every
solution
is
contained
in
a
contour
of
E =
constant.
E
=
0
is
again
a
single
point
at
which
E
is
the
absolute
minimum,
corresponding
to
the
pendulum
hanging
vertically
downwards
in
stable
equilibrium.
Again
E =
2g
contains
the
other
equilibrium
point,
where
the
pendulum
stands
vertically
upward
in
unstable
equilibrium,
and
at
this
point
E
is
stationary
but
not
minimal.
From
Morse
theory
(see
Chapter
2
and
Hirsch
[1976],
Milnor
[1963])
one
knows
that
for
0 < c <
2g
the
contour
E"
1
(c)
is
homeomorphic
to
s
3
•
The
spherical
pendulum
is
symmetrical
about
the
vertical
axis
through
the
pivot
point.
This
symmetry
manifests
itself
10

in
Eq.(l.l-4),
for
they
are
unaltered
if
we
replace~
by~+
k
(k
=
constant)
or
if
we
replace
~
and
~
by
-~
and
-~.
Thus
the
orthogonal
group
0(2)
acts
on
the
system
as
a
group
of
symmetries
about
the
vertical
axis.
Such
symmetries
can
reveal
important
features
of
the
phase-portrait.
Here
for
any
c
with
0 < c <
2g,
the
3-sphere
E-
1
(c)
is
partitioned
into
a
family
of
tori,
together
with
two
exceptional
circles
as
in
Fig.1.1.3.
This
decomposes
R
3
into
a
family
of
tori,
with
a
circle
through
p
and
q
and
the
line
1.
Combining
with
a
"point
at
co
"
turns
R
3
into
a
topological
3-sphere
and
the
line
1
into
a
topological
circle.
The
submanifolds
of
this
partition
are
each
generated
by
a
single
integral
curve
under
the
action
of
S0(2)
and
they
are
the
intersections
of
E-
1
(c)
with
the
contours
of
the
angular
momentum
function
on
TS
2
•
The
two
exceptional
circles
correspond
to
the
pendulum
revolving
in
a
horizontal
circle
in
two
opposite
directions.
Between
them
comes
a
form
corresponding
to
that
of
a
pendulum
in
the
various
planes
through
1.
z
Fig.
1.1.3
11
y

In
the
examples
given
above,
the
dynamical
state
of
the
system
is
represented
by
a
point
of
the
state
space
which
is
the
tangent
bundle
(such
as
s
1
x R
1
or
T(S
2
))
of
the
configuration
space
(5
1
or
s•
respectively).
And
the
equation
of
motion
represented
by
a
vector
field
on
the
state
space
and
its
integral
curves
give
the
possible
motions
of
the
system.
A
useful
way
of
visualizing
a
vector
field
v
on
an
arbitrary
manifold
X
is
to
imagine
a
fluid
flowing
on
X.
Let
us
assume
that
the
velocity
of
the
fluid
at
each
point
x e X
is
independent
of
time
and
equals
to
the
value
v(x).
Then
the
integral
curves
of
v
are
precisely
the
paths
followed
by
particles
of
the
fluid.
Let
¢(t,x)
be
the
point
of
X
reached
at
time
t
by
a
particle
of
the
fluid
that
leaves
X
au
time
o.
Obviously,
¢(O,x)
is
always
x.
Since
the
velocity
is
assumed
to
be
independent
of
time,
¢(s,y)
is
the
point
reached
at
time
s+t
by
a
particle
starting
at
y
at
time
t.
if
we
set
y =
¢(t,x),
as
the
particle
started
from
x
at
time
o,
then
¢(s,¢(t,x))
=
¢(s+t,x).
We
also
expect
smoothness
of
¢.
We
shall
make
these
observations
more
precise
when
we
discuss
one-parameter
groups
of
motion
in
Ch.
2.
The
map ¢ may
not
be
defined
on
the
whole
space
X x R,
because
particles
may
flow
off
X
in
a
finite
time.
But,
if
¢
is
a
well-defined
smooth
map
from
X x R
to
X
with
the
above
properties,
we
shall
call
it,
an
analogy
to
the
fluid,
a
smooth
flow
on
X:
othherwise,
it
is
a
partial
flow
on
x.
¢
is
the
integral
flow
of
v
or
the
dynamical
system
given
by
v.
If
¢ : X x R
~
X
is
a
smooth
flow
on
X,
then
for
any
t e
R, we may
define
a map
¢t
: X
~
X
by
¢t(x)
=
¢(t,x)
and
it
is
a
diffeomorphism
with
inverse
¢-t.
If
we
put
f = ¢
8
for
some a e R,
then
by
induction,
¢(na,x)
=
f"(x)
for
all
integers
n.
Thus,
if
a
is
small
and
non-zero,
we
often
get
a
good
idea
of
the
properties
of
¢
by
studying
the
iterates
f"
of
f
(just
as
real
events
can
be
represented
well
by
the
successive
still
frames
of
a
motion
picture).
The
theory
of
discrete
dynamical
systems
or
discrete
flow
resembles
the
12

theory
of
flow
in
many
ways;
and
we
shall
cover
both
of
them.
Now
let
us
turn
our
attention
to
an
example
of
a
dynamic
system
in
the
context
of
population
growth.
Let
us
look
at
the
simplest
example
of
the
rich
theory
of
interacting
populations,
the
predator-prey
model.
Let
us
imagine
an
island
populated
by
goats
and
wolves
only.
The
goats
survive
by
eating
the
island
vegetation
and
the
wolves
survive
by
eating
the
goats.
The
modeling
of
this
kind
of
population
system
goes
back
to
Volterra
in
response
to
the
observation
that
populations
of
species
often
oscillate.
Let
N
1
(t)
and
N
2
(t)
represent
the
populations
of
the
prey
(goats)
and
predators
(wolves),
respectively
.
Volterra
described
the
situation
in
the
following
way:
dN
1
(t)
/dt
=
aN
1
(t)
-
bN
1
(t)
N
2
(t)
dN
2
(t)jdt
= -
cN
2
(t)
+
dN
1
(t)N
2
(t)
(1.1-5)
where
the
constants
a,
b,
c
and
d
are
positive.
The
model
is
based
on
the
assumption
that
in
the
absence
of
predators
(wolves),
the
prey
(goats)
population
will
increase
exponentially
with
a
growth
rate
a.
Likewise,
in
the
absence
of
prey,
the
predator
population
will
diminish
at
a
rate
c.
When
both
populations
are
present,
the
frequency
of
"encounters"
is
assumed
to
be
proportional
to
the
product
of
the
two
populations.
Each
encounter
decreases
the
prey
(goats)
population
and
increases
the
predator
(wolves)
population.
The
effects
of
these
encounters
are
accounted
for
by
the
second
terms
in
the
differential
equations.
Of
course,
these
equations
are
highly
simplified
and
do
not
take
into
account
a
number
of
external
factors
such
as
general
environment
conditions,
supply
of
other
food
for
both
predator
and
prey,
migration
of
the
populations,
disease,
and
crowding.
An
important
application
of
a
model
of
this
type
is
the
study
and
control
of
pests
and
feed
on
agricultural
crops.
The
pest
population
is
often
controlled
by
introducing
predators,
and
such
a
predator-prey
model
often
forms
the
foundation
of
ecological
intervention.
The
nonlinear
dynamic
Eq.(1.1-5)
cannot
be
solved
13
