Lee K.K. Lectures on Dynamical Systems, Structural Stability and Their Applications
Подождите немного. Документ загружается.

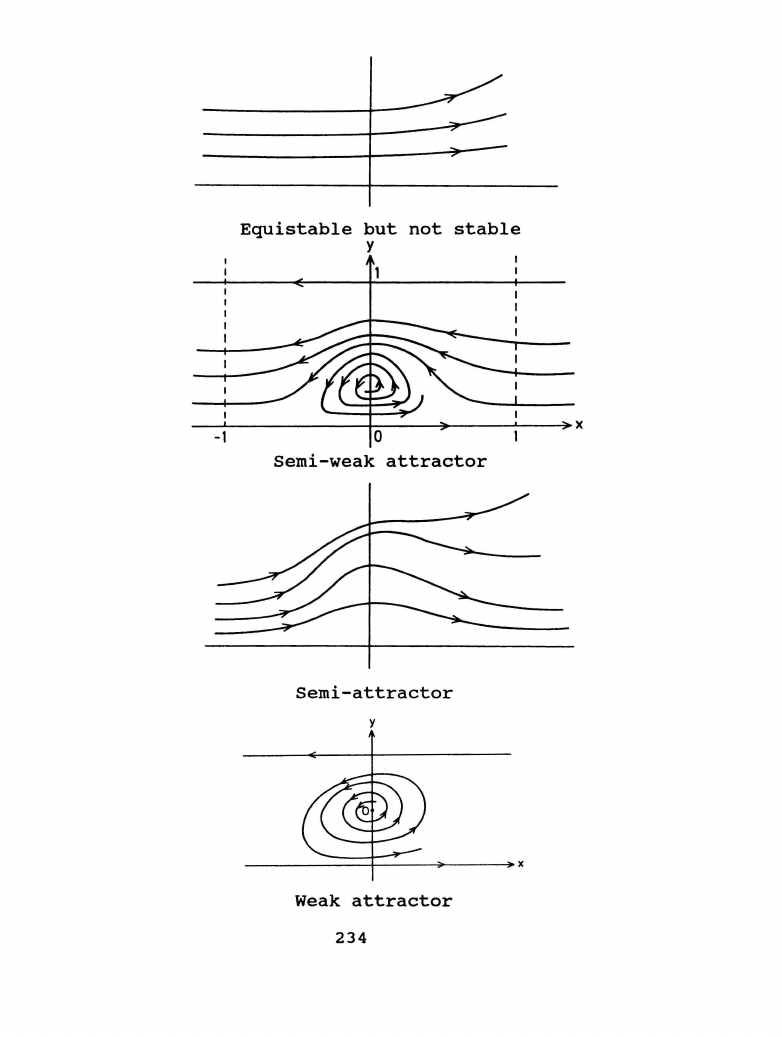
Equistable
but
not
stable
y
Semi-weak
attractor
Semi-attractor
Weak
attractor
234
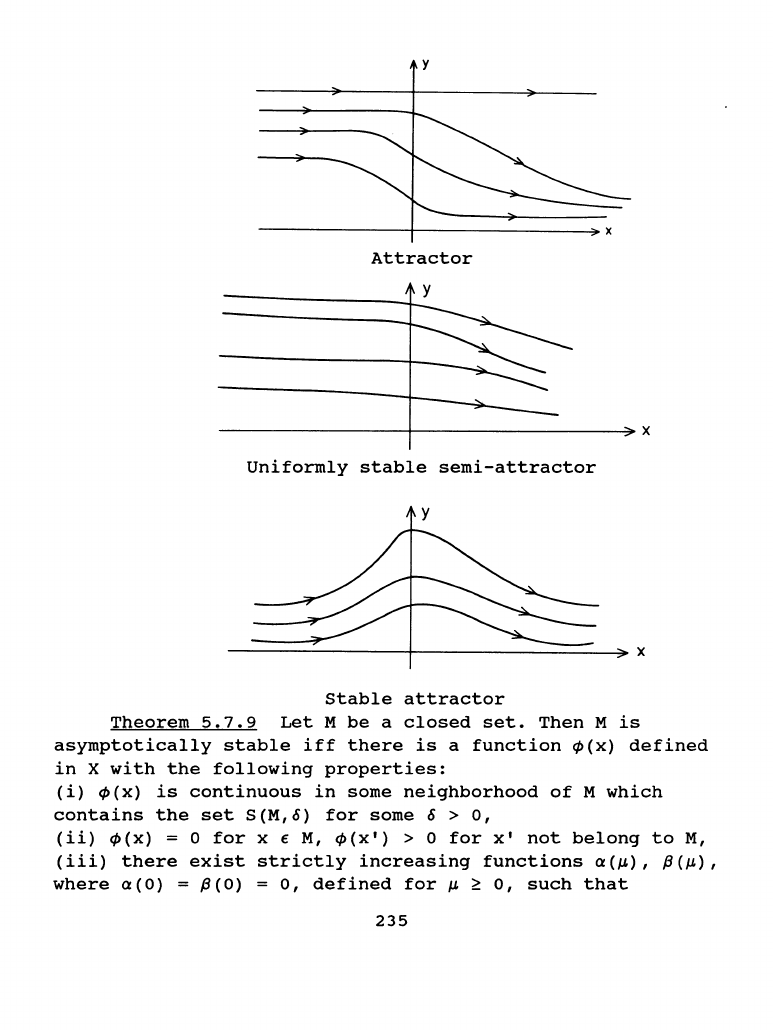
y
At
tractor
Uniformly
stable
semi-attractor
y
Stable
attractor
Theorem
5.7.9
Let
M
be
a
closed
set.
Then
M
is
asymptotically
stable
iff
there
is
a
function
¢(x)
defined
in
X
with
the
following
properties:
(i)
¢(x)
is
continuous
in
some
neighborhood
of
M
which
contains
the
set
S(M,o)
for
some
6 > o,
(ii)
¢(x)
= 0
for
x €
M,
¢(x')
> 0
for
x•
not
belong
toM,
(iii)
there
exist
strictly
increasing
functions
a(~),
PC~),
where
a(O)
=
P(O)
=
o,
defined
for
~
~
0,
such
that
235

a(d(x,M))
S
~(x)
S
P(d(x,M)),
(iv)
~(xt)
S
~(x)
for
all
x E X, t >
0,
and
there
is
a 6 > 0
such
that
if
x E
S(M,6)
- M
then
~(xt)
<
~(x)
fort>
0,
and
~(xt)
~
0
as
t
~
oo.
Theorem
5.7.10
Let
a
closed
invariant
set
M
be
asymptotically
stable.
Let
A(M) - M
(or
in
particular
the
space
X)
be
locally
compact
and
contain
a
countable
dense
subset.
Then
the
invariant
set
A(M) - M
is
parallelizable.
Proposition
5.7.11
Let
M
be
a
closed
invariant
uniformly
asymptotically
stable
subset
of
X
with
A(M)
as
its
region
of
attraction.
Then
A(M) - M
is
parallelizable.
In
the
following
we
shall
discuss
the
concepts
and
properties
of
relative
stability
and
attraction
of
a
compact
set.
X
is
assumed
to
be
locally
compact.
For
a
given
compact
set
M,
a
subset
of
X,
and
a
subset
U
of
X,
the
set
M
is
said
to
be:
(i)
stable
relative
to
U,
if
given
an
E > 0
there
exists
6 >
o,
such
that
r•(s(M,6)nU)
is
a
subset
of
S(M,e),
(ii)
a
weak
attractor
relative
to
u,
if
n(x)nM
+
o,
for
each
x e u,
(iii)
an
attractor
relative
to
u,
if
n(x)
+
o,
n(x)
is
a
subset
of
M,
for
each
x E
U,
(iv)
a
uniform
attractor
relative
to
U,
if
J+(x,U)
+
0,
J•(x,U)
is
a
subset
of
M,
for
each
x e
u,
(v)
asymptotically
stable
relative
to
u
if
M
is
a
uniform
attractor
relative
to
U
and
it
is
positively
invariant.
Note
that,
if
in
the
above
definitions
U
is
a
neighborhood
of
M,
then
the
stability,
weak
attraction,
attraction,
uniform
attraction
and
asymptotic
stability
of
M
relative
to
U
reduces
to
the
stability,
weak
attraction,
attraction,
uniform
attraction
and
asymptotic
stability
of
M
respectively.
Theorem
5.7.12
A
compact
subset
M
of
X
is
stable
relative
to
a
subset
u
of
X
iff
M
contains
o•(M,U).
Theorem
5.7.13
Let
a
subset
M
of
X
be
compact
and
such
that
Aw(M)
- M +
0.
Let
U
be
a
subset
of
Aw(M)
be
a
set
with
the
following
properties:
(i)
U
is
closed
and
positively
invariant;
(ii)
U n M +
o.
Then
the
set
o•(M,U)
is
compact
and
asymptotically
stable
relative
to
U.
236

Theorem
5.7.14
Let
a
subset
M
of
X
be
compact
and
positively
invariant
and
let
M'
be
the
largest
invariant
subset
contained
in
M.
Then
M'
is
a
stable
attractor,
relative
to
M.
For
example,
consider
a
limit
cycle
r
in
R
2
with
the
property
that
all
orbits
outside
the
unit
disk
bounded
by
the
limit
cycle
r,
has
r
as
their
sole
positive
limit
se~,
and
all
orbits
in
the
interior
of
the
disk
tend
to
the
equilibrium
point
o.
See
Fig.5.7.2.
We
shall
meet
this
auto-oscillatory
system
in
Section
7.2.
Suffice
to
note
that
if
U
is
the
complement
of
the
disk
bounded
by
r,
then
r
is
relatively
stable
with
respect
to
U.
Note
also
that
if
r
is
an
asymptotically
stable
limit
cycle,
then
r
is
stable
with
respect
to
every
component
of
R
2
-
r.
Fig.5.7.2
These
considerations
lead
to
the
following
definition
and
theorem.
Let
M
be
a
compact
subset
of
X.
M
is
said
to
be
component-wise
stable
if
M
is
relative
stable
with
respect
to
every
component
of
X -
M.
Theorem
5.7.15
Let
a
compact
subset
M
of
X
be
positively
stable.
Then
M
is
component-wise
stable.
The
converse
is
not
true
in
general.
The
following
example
illustrates
this
conclusion.
Let
X
be
a
subset
of
R
2
given
by
X=
{(x,y)
£ R
2
:
y =
1/n,
n
is
any
integer,
or
y =
0}.
Clearly
the
space
is
a
metric
space
with
the
distance
between
any
two
points
being
the
Euclidean
distance
between
the
points
in
R
2
•
We
can
define
a
dynamical
system
on
X
by
dxjdt
= IYI,
dyjdt
=
0.
Then
the
set
{(0,0)}
in
X
is
237

component-wise
stable,
but
is
not
stable.
It
is
then
nature
to
ask
under
what
conditions
the
converse
of
Theorem
5.7.15
is
true.
We
first
introduce
the
following
definition,
then
followed
by
a
couple
of
theorems.
Let
M
be
a
compact
subset
of
X.
We
say
the
pair
(M,X)
is
stability-additive
if
the
converse
of
Theorem
5.7.15
holds
for
every
dynamical
system
defined
on
X
which
admits
M
as
an
invariant
set.
Theorem
5.7.16
The
pair
(M,X)
is
stability-additive
if
X - M
has
a
finite
number
of
components.
Theorem
5.7.17
The
pair
(M,X)
is
stability-additive
if
X - M
is
locally
connected.
5.8
Almost
periodic
motions
We
have
discussed
periodicity
and
recurrence.
In
the
following
we
shall
briefly
discuss
the
concept
intermediate
between
them,
namely
that
of
almost
periodicity.
For
convenience,
we
assume
that
the
metric
space
X
is
complete.
A
motion
~x
is
said
to
be
almost
periodic
if
for
every
E
> 0
there
exists
a
relatively
dense
subset
of
numbers
{rn}
called
displacements,
such
that
d(xt,
x(t+rn)l
< e
for
all
t
e R
and
each
rn.
It
is
clear
that
periodic
motion
and
fixed
points
are
special
cases
of
almost
periodic
motions.
And
it
is
also
easy
to
show
that
every
almost
periodic
motion
is
recurrent.
We
shall
show
that
not
every
recurrent
motion
is
almost
periodic,
and
an
almost
periodic
motion
need
not
be
periodic.
The
following
theorems
show
how
stability
is
deeply
connected
with
almost
periodic
motions.
Theorem
5.8.1
Let
the
motion
~x
be
almost
periodic
and
let
the
closure
of
r(x)
be
compact.
Then:
(i)
every
motion
~Y
withy
E
closure
of
r(x),
is
almost
periodic
with
the
same
set
of
displacements
{rn}
for
any
given
e > o,
but
with
the
strict
inequality
<
replaced
by
~;
(ii)
the
motion
~x
is
stable
in
both
directions
in
the
closure
of
r(x).
Corollary
5.8.2
If
M
is
a
compact
minimal
set,
and
if
238

one
motin
in
M
is
almost
periodic,
then
every
motion
in
M
is
almost
periodic.
Corollary
5.8.3
If
M
is
a
compact
minimal
set
of
almost
periodic
motions,
then
the
motions
through
M
are
uniformly
stable
in
both
directions
in
M.
Theorem
5.8.4
If
a
motion
~x
is
recurrent
and
stable
in
both
directions
in
r(x),
then
it
is
almost
periodic.
Theorem
5.8.5
If
a
motion
~x
is
recurrent
and
positively
stable
in
r(x),
then
it
is
almost
periodic.
Theorem
5.8.6
If
the
motions
in
r(x)
are
uniformly
positively
stable
in
r(x)
and
are
negatively
Lagrange
stable,
then they
are
almost
periodic.
A
semi-orbit
r•(x)
is
said
to
uniformly
approximate
its
limit
set,
n(x),
if
given
any
e > o,
there
is
aT=
T(e)
> 0
such
that
n(x)
is
a
subset
of
S(x[t,t+T],e)
for
each
t e
R+.
We
want
to
find
out
under
what
conditions
a
limit
set
is
compact
and
minimal.
We
have
the
following:
Theorem
5.8.7
Let
the
motion
~x
be
positively
Lagrange
stable.
Then
the
limit
set
n(x)
is
minimal
iff
the
semi-orbit
r•(x)
uniformly
approximates
n(x).
Theorem
5.8.8
Let
the
motion
~x
be
positively
Lagrange
stable,
and
let
the
motions
in
r•(x)
be
uniformly
positively
stable
in
r•(x).
If
furthermore
r•(x)
uniformly
approximates
n(x),
then
n(x)
is
a
minimal
set
of
almost
periodic
motions.
It
should
be
pointed
out
that
no
necessary
and
sufficient
conditions
are
known
yet.
In
closing,
let
us
discuss
an
example
of
an
almost
periodic
motion
which
is
neither
a
fixed
point
nor
a
periodic
motion.
Consider
a
dynamical
system
defined
on
a
torus
by
the
following
set
of
simple
differential
equations:
d~/dt
=
1,
dB/dt
=
a,
where
a
is
irrational.
For
any
point
p
on
the
torus,
the
closure
of
r(p)
=
the
torus,
and
since
a
is
irrational,
no
orbit
is
periodic.
The
torus
is
thus
a
minimal
set
of
recurrent
motions.
To
show
that
the
motions
are
almost
periodic,
we
note
that
if
p
1
=
(~
1
,8
1
),
and
p
2
=
(~
2
,8
2
),
then
239

d(p,t,2t)
=
(¢,
- ¢2)
2
+
(91
- 92)
2
=
d(p,,p2)
1
where
the
values
of
¢
1
- ¢
2
and
9
1
- 9
2
ae
taken
as
the
smallest
in
absolute
value
of
the
differences,
and
also
note
that
any
motion
on
the
torus
is
given
by
¢ = ¢
0
+
t,
9 = 9
0
+
at.
Thus
the
motions
are
uniformly
stable
in
both
directions
in
the
torus.
Thus,
from
Theorem
5.8.4,
the
torus
is
a
minimal
set
of
almost
periodic
motions.
In
Section
4.4
we
have
derived
the
van
der
Pol's
equation
of
the
nonlinear
oscillator.
Cartwright
[1948]
and
her
later
series
of
papers
dealt
with
a
generalized
van
der
Pol's
equation
for
forced
oscillations.
The
periodic
and
almost
periodic
orbits
are
obtained.
For
detail,
see
also
Guckenheimer
and
Holmes
[1983].
Krasnosel'skii,
Burd
and
Kolesov
[1973]
discusses
broader
classes
of
nonlinear
almost
periodic
oscillations.
The
book
by
Nayfeh
and
Mock
[1979]
gives
many
detailed
discussions
on
nonlinear
oscillations.
The
Annual
of
Mathematics
series
on
nonlinear
oscillations
are
highly
recommended
for
further
reading
[Lefschetz
1950,
1956, 1958,
1960].
Indeed,
there
are
many
current
problems,
such
as
in
phase
locked
laser
arrays,
where
some
of
the
results
are
very
applicable
to
the
problems.
We
shall
briefly
point
this
out
in
the
next
chapter.
Most
of
this
chapter
is
based
on
several
chapters
of
Rouche,
Habets
and
Laloy
[1977].
This
is
still
one
of
the
best
sources
for
Liapunov•s
direct
method.
240

Chapter
6
xntroduction
to
the
General
Theory
of
structural
stability
6.1
xntroduction
However
complex
it
may
seem,
our
universe
is
not
random,
otherwise
it
would
be
futile
to
study
it.
Instead,
it
is
an
endless
creation,
evolution,
and
annihilation
of
forms
and
patterns
in
space
which
last
for
certain
periods
of
time.
one
of
the
central
goals
of
science
is
to
explain,
and
if
possible,
to
predict
such
changes
of
form.
Since
the
formation
of
such
structures
or
patterns
and
their
evolutional
behavior
are
"geometric"
phenomena,
uncovering
their
common
bases
is
a
topological
problem.
But
the
existence
of
topological
principles
may
be
inferred
from
various
analogies
found
in
the
critical
behavior
of
systems.
It
should
be
emphasized
that
recognizing
analogies
is
an
important
source
of
knowledge
as
well
as
an
important
methodology
of
acquiring
knowledge.
There
is
a
striking
similarity
among
the
instabilities
of
convection
patterns
in
fluids,
cellular
solidification
fronts
in
crystal
growth,
vortex
formation
in
superconductors,
phase
transitions
in
condensed
matter,
particle
physics,
laser
physics,
nonlinear
optics,
geophysical
formations,
biological
and
chemical
patterns
and
diffusion
fronts,
economical
and
sociological
rhythms,
and
so
forth.
Their
common
characteristic
is
that
one
or
more
behavior
variables
or
order
parameters
undergo
spontaneous
and
discontinuous
changes
or
cascades,
if
competing,
but
slowly
and
continuously
control
parameters
or
forces
cross
a
bifurcation
set
and
enter
conflicting
regimes.
Consequently,
an
initially
quiescent
system
becomes
unstable
at
critical
values
of
some
control
variables
and
then
restabilize
into
a
more
complex
space
or
time-dependent
configuration.
If
other
control
parameters
cause
the
disjoint
bifurcation
branches
to
interact,
then
multiple
degenerate
bifurcation
points
produce
higher
order
instabilities.
Then,
the
system
undergoes
additional
transitions
into
more
complex
states,
241

g~v~ng
rise
to
hysteresis,
resonance
and
entramment
effects.
These
ultimately
lead
to
states
which
are
intrinsically
chaotic.
In
the
vicinity
of
those
degenerate
bifurcation
points,
a
system
is
extremely
sensitive
to
small
changes,
such
as
imperfection,
or
external
fluctuations
which
lead
to
symmetry
breaking.
Consequently,
the
system
enhances
its
ability
to
perceive
and
to
adapt
its
external
environment
by
forming
preferred
patterns
or
modes
of
behavior.
Prigoqine's
concept
of
dissipative
structures
[1984],
Haken's
synergetics
[1983],
and
Them's
catastrophe
theory
[1973]
are
most
prominent
among
the
theoretical
study
of
these
general
principles.
As
we
have
discussed
earlier,
the
guiding
idea
of
a
stable
system
is
to
find
a
family
of
dynamical
systems
which
contains
"almost
all"
of
them,
yet
can
be
classified
in
some
qualitative
fashion.
It
was
conjectured
that
structurally
stable
systems
would
fit
the
bill.
Although
it
turns
out
not
to
be
true
except
for
low
dimensional
cases,
structural
stability
is
such
a
natural
property,
both
mathematically
and
physically,
that
it
still
holds
a
central
place
in
the
theory
of
dynamical
systems.
As
we
have
pointed
out
in
Section
1.2,
there
is
the
doctrine
of
stability
in
which
structurally
unstable
systems
are
regarded
as
suspicious.
This
doctrine
states
that,
due
to
measurement
uncertainties,
etc.,
a
model
of
a
physical
system
is
valuable
only
if
its
qualitative
properties
do
not
change
under
small
perturbations.
Thus,
structural
stability
is
imposed
as
a
prior
restriction
on
"good"
models
of
physical
phenomena.
Nonetheless,
strict
adherence
to
such
doctrines
is
arguable
to
say
the
least.
It
is
very
true
that
some
model
dynamical
systems,
such
as
an
undamped
harmonic
oscillator,
the
Lotka-Volterra
equations
of
the
predator-prey
model,
etc.,
are
not
good
models
for
the
phenomena
they
are
supposed
to
represent
because
perturbations
give
rise
to
different
qualitative
features.
Nonetheless,
these
systems
are
indeed
realistic
models
for
242

the
chaotic
behavior
of
the
corresponding
deterministic
systems
since
the
presumed
strange
attractors
of
these
systems
are
not
structurally
stable.
If
we
turn
to
the
other
side
of
the
coin,
as
we
have
also
pointed
out
in
Section
1.2,
since
the
systems
are
not
structurally
stable,
details
of
their
dynamical
evolutions
which
do
not
persist
under
perturbations
may
not
correspond
to
any
verifiable
physical
properties
of
the
systems.
Consequently,
one
may
want
to
reformulate
the
stability
doctrine
as
the
only
properties
of
a Cor a
family
of)
dynamical
systemCs>
which
are
physically
Cor
quantitatively>
relevant
are
those
preserved
under
perturbations
of
the
systemCs).
Clearly,
the
definition
of
(physical)
relevance
depends
on
the
specific
problem
under
study.
Therefore,
we
will
take
the
spirit
that
the
discussions
of
structural
stability
requires
that
one
specify
the
allowable
perturbations
to
a
given
system.
The
two
main
ingredients
of
structural
stability
are
the
topology
given
to
the
set
of
all
dynamical
systems
and
the
equivalence
relation
placed
on
the
resulting
topological
space.
The
former
is
the
cr
topology
(1
S r S
~).This
topology
has
been
discussed
in
Chapter
3,
and
the
idea
in
our
context
is
clear.
For
instance,
two
diffeomorphisms
are
cr-close
when
their
values
and
values
of
corresponding
derivatives
up
to
order
r
are
close
at
every
point.
Once
we
have
defined
the
cr
topology,
we
may
be
able
to
be
more
specific
about
what
we
mean
by
"almost
all"
of
the
systems.
The
latter
attribute
is
topological
equivalence
for
flows
and
topological
conjugacy
for
diffeomorphisms.
Before
we
get
into
a
more
general
discussion
of
structural
stability
for
manifolds,
diffeormorphisms,
function
spaces
of
maps,
and
so
forth,
let
us
discuss
the
concept
for
R
0
•
Let
Fe
cr(R
0
),
we
want
to
specify
what
we
mean
by
a
perturbation
G
of
F.
Let
F
be
as
above,
r,
k
are
positive
integers,
k S
r,
and
e >
o,
then
G
is
a
ck
perturbation
of
size
e
if
there
is
a
compact
subset
K
of
R
0
such
that
F = G
243
