Лазарев Ю.Ф. Mатематическое моделирование физических процессов и технических систем в MATLAB

Подождите немного. Документ загружается.

321

Основные действия по численному интегрированию дифференциальных уравнений (14) сосредоточены в

подсистемах

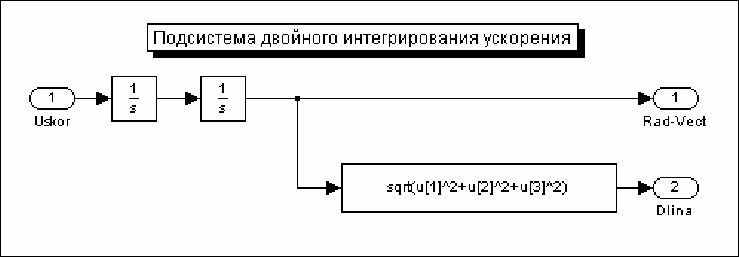
Uravnenye 21 и Uravnenye 32. Здесь (рис. 7. 98) производится двойное интегрирование

ускорений, а также вычисляется текущее расстояние (длина вектора) между вторым и первым телами. Входной

величиной обоих подсистем является векторная величина, элементы которого представляют собой проекции

вектора ускорения на оси X, Y и Z. Выходных величин две. Одна их них – вектор из трех элементов,

являющихся текущими проекциями радиус-вектора

на те же оси. Второй выход – скалярная величина – длина

этого радиус-вектора.

Рис. 7. 98. Блок-схема подсистемы Uravnenye 21

Блок, реализующий вычисление длины вектора по его составляющим, реализован на основе блока

Fcn из

раздела User-Defined Functions.

Примечание. При написании арифметических выражений в окнах настраивания блоков Simulink

используются правила М-языка. Однако

указание индексов для векторов и матриц

должно осуществляться в квадратных скобках

(а не в круглых, как в М-языке)

Важной и характерной особенностью этих подсистем, отличающей их от использованной ранее подсистемы

Маятник

(рис. 7. 89), является то, что в них интегрируется не скалярная функция времени, а векторная,

состоящая сразу из трех скалярных величин. Например, в подсистеме

Uravnenye 21 производится

одновременное интегрирование ускорений

и . Достигается это с помощью только двух блоков

Integrator

. Для этого достаточно в блоке настраивания интеграторов ввести в качестве начального условия

не одну величину, а вектор из трех величин, каждая из которых является начальным условием

соответствующего элемента вектора, поступающего на вход интегратора. Например, вектором начальных

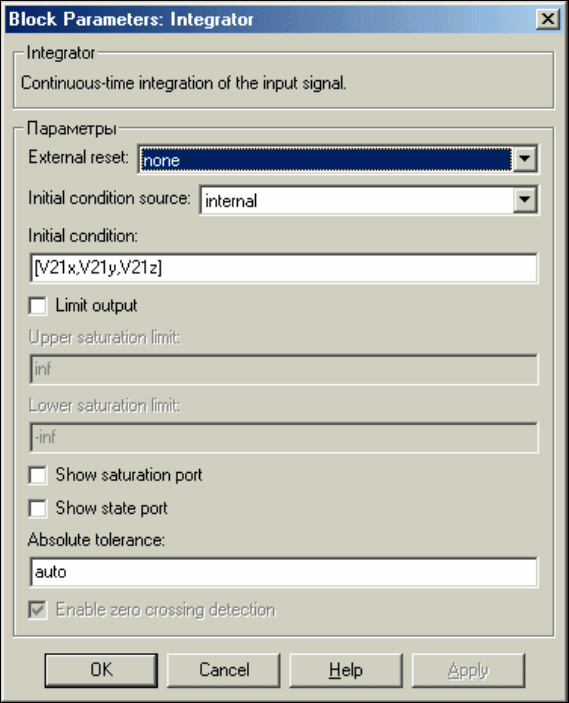
условий для первого интегратора является

[V21x,V21y,V21z] (см. рис. 7. 99).

2121

, yx

′′′′

′′

322

Рис. 7. 99. Окно настраивания первого блока Integrator подсистемы Uravnenye 21

Аналогично, во втором интеграторе установлен вектор [X210,Y210,Z210] начальных условий.

То же сделано в подсистеме

Uravnenye 32, которая вычисляет текущие составляющие вектора ,

полученные двойным интегрированием ускорения

. Здесь в интеграторах установлены начальные условия

в виде векторов

[V32x,V32y,V32z]

[X320,Y320,Z320].

′′

Подсистемы

Prav 21 и

Prav 32

формируют правые части первого и второго уравнений (14), т. е. ускорения

в виде вектора из трех элементов. Выходная величина у этих подсистем – одна. Например, в подсистеме

Prav

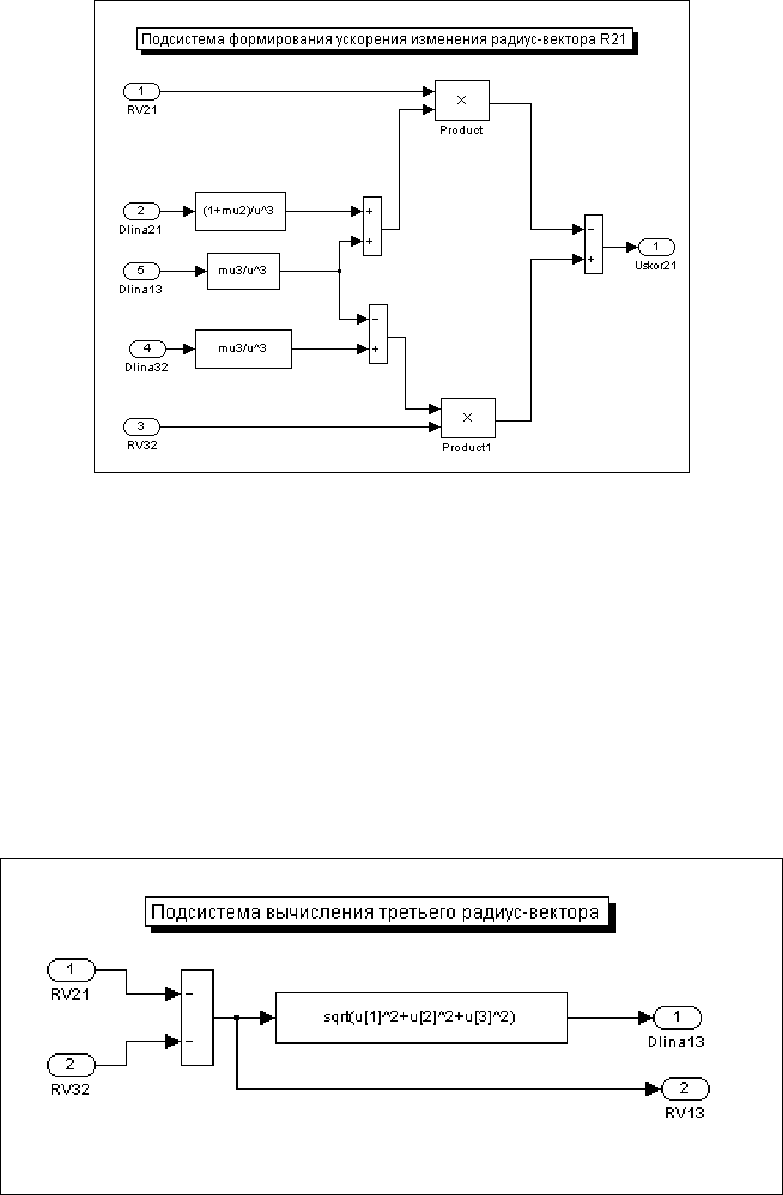
(рис. 7. 100) выходом является вектор Uskor21, составляющими которого являются проекции ускорения на

оси X, Y и Z.

323

Рис. 7. 100. Блок-схема подсистемы Prav 21

Входами являются два вычисленных ранее вектора RV21 и RV32, состоящие из проекций радиус-векторов

, и три скалярные величины, равные текущим значениям длин трех радиус векторов, соединяющих три

тела.

В подсистеме

Prav 21 используются три блока типа Fcn для вычисления коэффициентов при векторах в

правой части первого уравнения (14) и два блока

Product

для перемножения вектора на скалярный

коэффициент.

Блок схема подсистемы

RV13

, вычисляющей вектор

и его длину по известным векторам и ,

приведена на рис. 7. 101.

Рис. 7. 101. Блок-схема подсистемы RV13

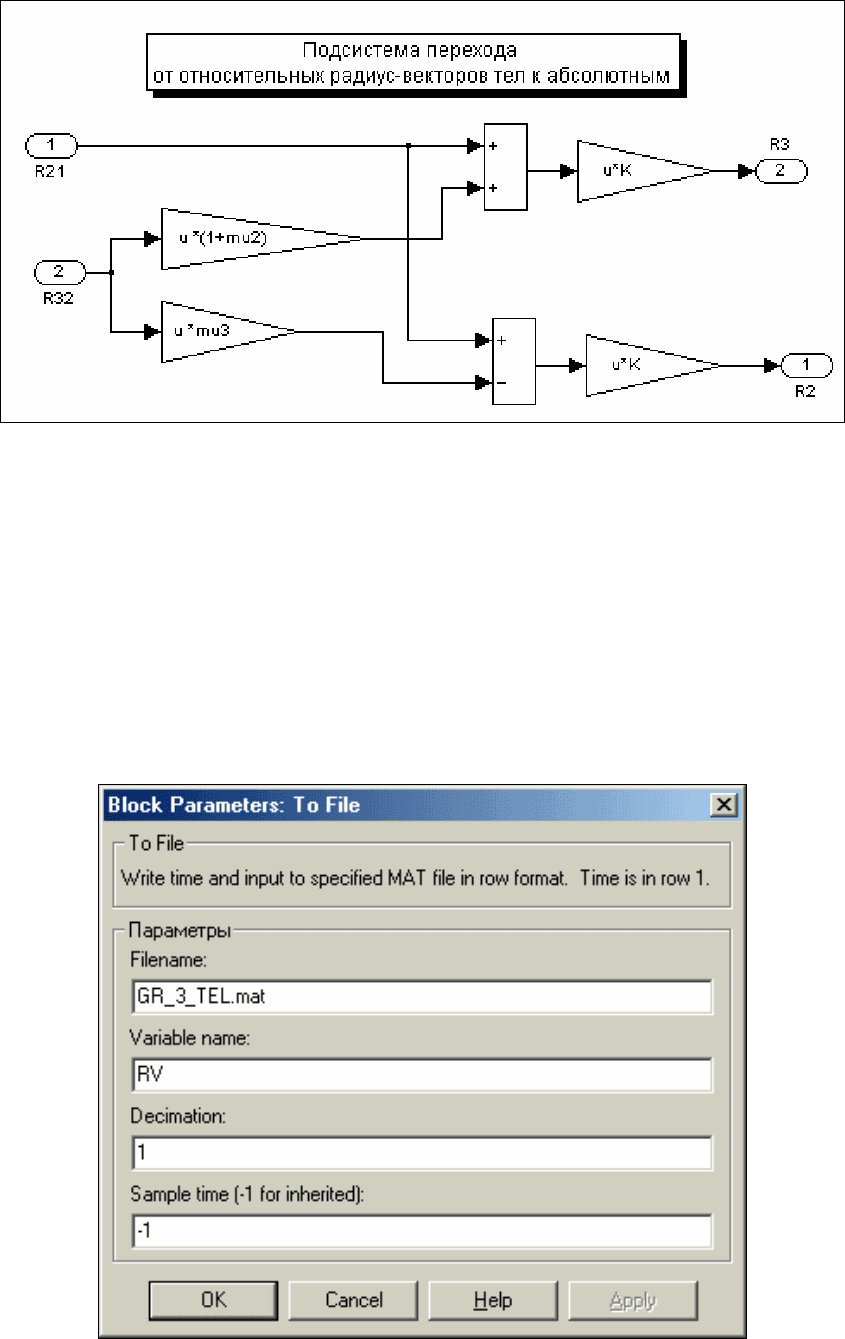
На рис. 7.102 показана блок-схема подсистемы Absolute Coordinates. Она вычисляет абсолютные

координаты второго и третьего тела относительно центра масс системы трех тел.

324

Рис. 7. 102. Блок-схема подсистемы Absolute Coordinates

Блок To File производит запись поступающих на его вход данных в МАТ-файл GR_3_TEL. mat. Эти данные

записываются на диск в виде матрицы под именем RV (рис. 7. 103) в следующем порядке:

- первую строку образует массив значений модельного времени, для которых вычислены подаваемые на

вход блока величины (хотя, как видно из рис. 7.97, на вход не подается время);

- вторую

строку образуют значения первого элемента входного векторного сигнала (ему соответствует

верхний сигнал, поступающий на вход блока Mux, выходной сигнал которого поступает на вход блока

File

), соответствующие моментам времени, записанным в первой строке;

- остальные строки заполняются значениями остальных элементов векторного сигнала входа в порядке

следования элементов этого вектора.

Рис. 7. 103. Заполнение окна настраивания блока To File

Это обстоятельство следует учитывать при считывании данных из сформированного МАТ-файла.

325

Для того, чтобы провести моделирование по созданной S-модели и оформить графически полученные

результаты следует произвести следующие операции:

1) ввести исходные данные в рабочее пространство;

2) запустить S-модель GR_3_TEL.mdl на моделирование; при этом результаты моделирования будут

записаны в МАТ-файл GR_3_TEL. mat;

3) загрузить содержимое МАТ-файла GR_3_TEL. mat в рабочее пространство, введя в командном

окне MatLab команду

load GR_3_TEL

при этом все данные, записанные в этом МАТ-файле, будут записаны в рабочее пространство в виде

матрицы под именем RV размером (16×n), где n – размер вектора значений времени;

4) используя данные матрицы RV, создать графическое и текстовое оформление результатов

моделирование в графическом окне MatLab.

Все эти операции можно автоматизировать, запрограммировав их в отдельной М-программе, которую

удобно

оформить в виде М-файла GR_3_TEL_upr (управляющая программа для S-модели GR_3_TEL). При этом

вызвать на моделирование S-модель из программы можно с помощью команды

sim('имя_S-модели')

Ниже приведен текст управляющей программы.

% GR_3_TEL_upr

% Программа управления для S-модели GR_3_TEL

% Лазарев Ю. Ф. 25-01-2004

% 1. Ввод данных в рабочее пространство

mu2=0.1; mu3=0.01;

X210=1; Y210=0; Z210=0;

V21x=0; V21y=1; V21z=0;

X320=0.1; Y320=0.0; Z320=0;

V32x=0; V32y=-1; V32z=0;

% 2. Запуск S-модели

sim('GR_3_TEL')

% 3. Загрузка МАТ-файла

load GR_3_TEL;

% 4. Присвоение значений из данных МАТ-файла новым переменным

t=RV(1,:);

X21=RV(2,:); Y21=RV(3,:); Z21=RV(4,:);

X32=RV(5,:); Y32=RV(6,:); Z32=RV(7,:);

X13=RV(8,:); Y13=RV(9,:); Z13=RV(10,:);

X2=RV(11,:); Y2=RV(12,:); Z2=RV(13,:);

X3=RV(14,:); Y3=RV(15,:); Z3=RV(16,:);

n=length(t);

% 5. Построение графика зависимости координат второго тела

% движения второго и третьего тел

subplot(2,2,1)

plot(t,X21,t,Y21,'--',t,Z21,'.'), grid

title('Движение второго тела относительно первого')

xlabel('Время (безразмерное)')

ylabel('Координаты (

безразмерные)')

legend('X','Y','Z',0)

% 6. Построение графика зависимости координат второго тела

% относительно первого от времени

subplot(2,2,3)

n1=round(n);

plot(t(1:n1),X32(1:n1),t(1:n1),Y32(1:n1),...

'—',t(1:n1),Z32(1:n1),'.'),grid

title('Движение третьего тела относительно второго')

xlabel('Время (безразмерное)')

ylabel('Координаты (безразмерные)')

legend('X','Y','Z',0)

% 7. Построение пространственных траекторий

% относительно первого от времени

subplot(4,4,[3,4,7,8,11,12])

plot3(X2,Y2,Z2,'.',X3,Y3,Z3), grid

title('Движение трех гравитирующих тел','FontSize',14)

xlabel('Координата Х')

ylabel('Координата Y')

zlabel('Координата Z')

legend('первое тело','второе тело',0)

326

% 8. Вывод текстового оформления

subplot(4,4,[15,16])

axis('off')

h= text(0,1.0,'Массовые параметры (относительные):');

h= text(-0.1,0.9,['mu1 = 1; ',sprintf('mu2 = %g; ',mu2),sprintf('mu3 = %g',mu3)]);

h= text(0.0,0.8,'Начальные координаты (безразмерные):');

h= text(-0.1,0.7,['второго тела относительно первого:',...

sprintf('X21 = %g; ',X210),sprintf('Y21 = %g; ,Y210),...

sprintf('Z21 = %g; ',Z210)]);

h= text(-0.1,0.6,['третьего тела относительно второго: ',

sprintf('X32 = %g; ',X320),sprintf('Y32 = %g; ',Y320),...

sprintf('Z32 = %g; ',Z320)]);

h= text(0,0.5,'Начальные скорости (безразмерные):');

h= text(-0.1,0.4,['второго тела относительно первого: ',...

sprintf('V21x = %g; ',V21x),sprintf('V21y = %g; ',V21y),...

sprintf('V21z = %g; ',V21z)]);

h= text(-0.1,0.3,['третьего тела относительно второго: ',...

sprintf('V32x = %g; ',V32x),sprintf('V32y = %g; ',V32y),...

sprintf('V32z = %g; ',V32z)]);

h= text(-0.1,0.1,'_____________________________________________ ');

h= text(-0.1,-0.1,'Программа GR-3-TEL-upr Автор - Лазарев Ю. Ф. 25-01-2004');

h= text(-0.1,-0.2,' ___________________________________________ ');

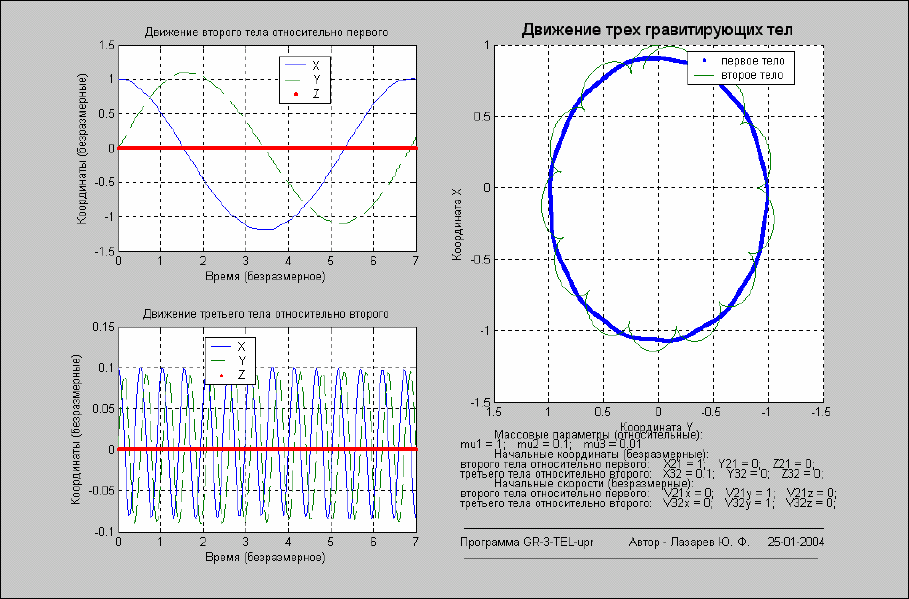
Запуск этой программы позволяет сразу получать результаты моделирования в виде, приведенном на рис. 7.

104…7. 106.

Рис. 7. 104. Плоское орбитальное движение трех тел в одном направлении

327

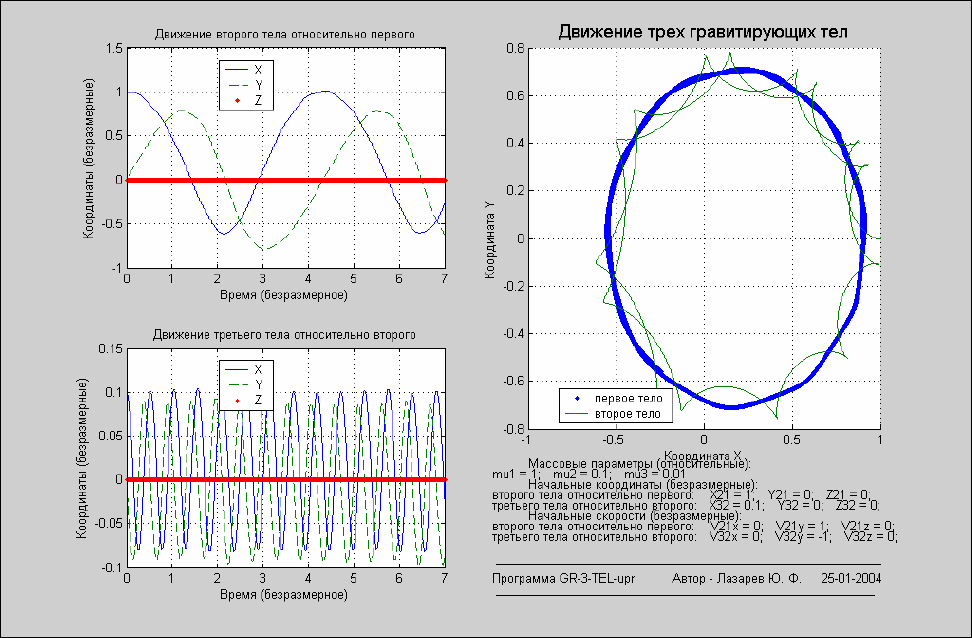
Рис. 7. 105. Плоское орбитальное движение трех тел в противоположных направлениях

Представленные результаты соответствуют трем случаям:

1) относительные орбитальные движения второго тела относительно первого и третьего относительно

второго происходят в одной плоскости (XY) в одном направлении (орбитальные моменты

однонаправлены – вдоль оси Z);

2) указанные орбитальные движения происходят в одной плоскости (XY) в противоположных

направлениях (орбитальные моменты

направлены противоположно);

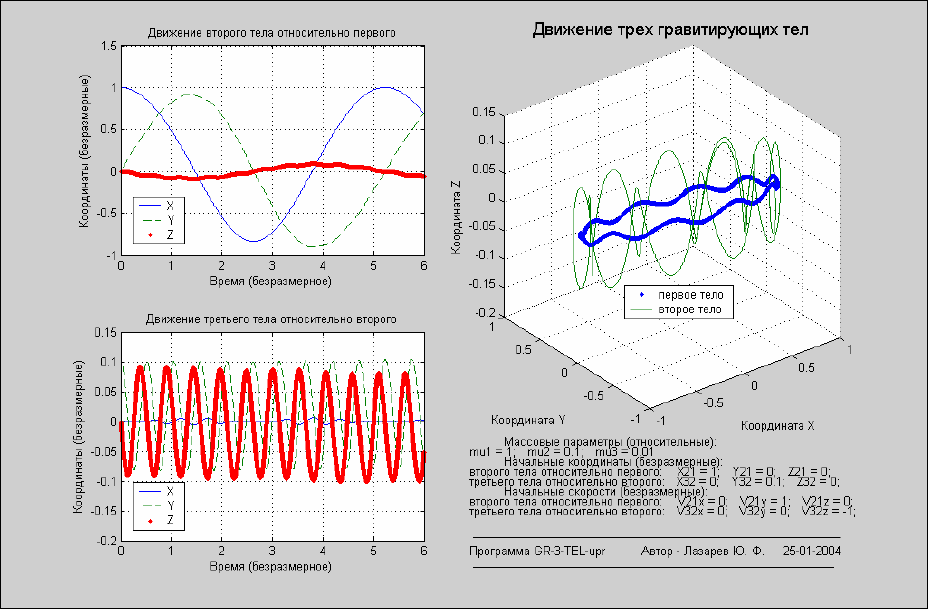
3) указанные орбитальные движения происходят во взаимно-перпендикулярных плоскостях.

Во всех случаях отношение масс тел первого, второго и третьего тел равно 100:10:1.

Относительные начальные скорости тел во всех случаях приняты одинаковыми по величине (

328

Рис. 7. 106. Орбитальное движение в случае перпендикулярности плоскостей орбит

Обратите внимание на различия в параметрах орбиты среднего (второго) тела и периода этого орбитального

движения.

7.4. Вопросы для самопроверки

1. Каковы преимущества использования пакета Simulink для решения вычислительных задач по сравнению с

программированием их непосредственно в среде MatLab?

2. Присутствие блоков каких разделов библиотеки SIMULINK совершенно необходимо в блок-схеме любой

S-модели?

3. Каково основное предназначение блоков раздела Source библиотеки SIMULINK?

3. Каково основное предназначение блоков раздела Sinks библиотеки SIMULINK?

4. Блоки какого раздела библиотеки SIMULINK

обеспечивают возможность пользователю создавать

собственные блоки?

5. Что такое подсистема и как ее создать?

6. Какими средствами можно обеспечить передачу данных из среды MatLab в S-модель и обратно?

7. В чем основное функциональное отличие блока

Fcn от блока MATLAB Fcn?

8. В чем главное преимущество блока

S-Function по сравнению со всеми остальными блоками библиотеки

SIMULINK, позволяющими пользователю создавать собственные блоки?

9. В чем заключаются преимущества использования подсистем?

10. Можно ли обеспечить одновременное интегрирование нескольких процессов одним блоком Integrator?

329

Урок 8. Взаимодействие MatLab c Simulink

Объединение S-моделей с программами MatLAB

Создание библиотек S-блоков пользователя

Примеры использования библиотеки пользователя

Вопросы для самопроверки

330

Как уже отмечалось, моделирование процессов с помощью S-моделей, несмотря на весьма значительные

удобства и преимущества, имеют и некоторые существенные недостатки.

К преимуществам использования

Simulink

-моделей относятся:

- весьма удобный, наглядный и эффективный способ образования программ моделирования даже довольно

сложных динамических систем – визуальное программирование, - путем сборки блок-схемы системы из

стандартных готовых блоков;

- довольно удобные и наглядные средства вмешательства в готовую блок-схему системы с целью ее

преобразования или получения дополнительной информации об изменении

промежуточных процессов;

широкий набор эффективных программ решателей (Solvers, методов численного интегрирования)

дифференциальных уравнений (с фиксированным шагом интегрирования, с переменным шагом, а также

решателей так называемых «жестких» систем дифференциальных уравнений);

- отсутствие необходимости в специальной организации процесса численного интегрирования;

уникальные возможности интегрирования нелинейных систем с «существенными» нелинейностями

(когда нелинейная зависимость

имеет скачкообразный характер);

- весьма быстрое и удобное получение графической информации об изменении моделируемых величин по

аргументу (времени).

Недостатками же использования S-моделей являются:

- жесткая и неудобная форма графического представления сигналов в блоках

Scope и XY Graph (в

отличие от средств среды MatLab);

невозможность автоматической (программной) обработки полученных результатов многоразового

моделирования одной или нескольких S-моделей;

- невозможность рациональной организации процесса изменения исходных данных S-модели и параметров

ее блоков (например, в диалоговой форме).

Кроме того, для отдельных видов дифференциальных уравнений намного удобнее, проще и быстрее составлять

процедуры их

правых частей в виде программы, чем составлять соответствующую блок-схему.

Указанное свидетельствует о том, что программная реализация процесса моделирования и моделирования в

виде S-моделей имеют взаимодополняющие свойства. Желательно уметь объединять преимущества этих двух

средств моделирования, соединяя программную реализацию с использованием S-моделей.

8.1. Объединение S-моделей с программами MatLAB

Очевидно, чтобы осуществить объединение программы с S-моделью надо иметь в наличии:

- средства передачи данных из среды MatLab в S-модель и обратно;

- средства запуска процесса моделирования S-модели из среды MatLab, а также изменения

параметров моделирования из этой среды;

- средства вызова программ MatLab из S-модели;

- средства создания S-блоков не только из других готовых блоков, а и путем использования программ,

написанных на М-языке MatLab.

Рассмотрим подробнее эти средства, предоставляемые системой MatLab.

8.1.1. Управление процессом моделирования в системе Simulink

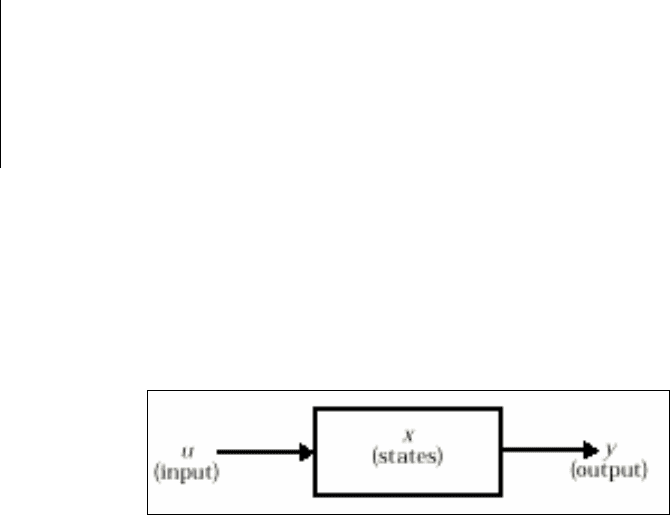
Каждый блок S-модели имеет такие внутренние характеристики (рис. 8.1):

- вектор входных величин u;

вектор выходных величин y;

вектор состояния x.

Рис. 8. 1. Схема взаимодействия величин, определяющих текущее состояние S-блока