Лазарев Ю.Ф. Mатематическое моделирование физических процессов и технических систем в MATLAB
Подождите немного. Документ загружается.

311
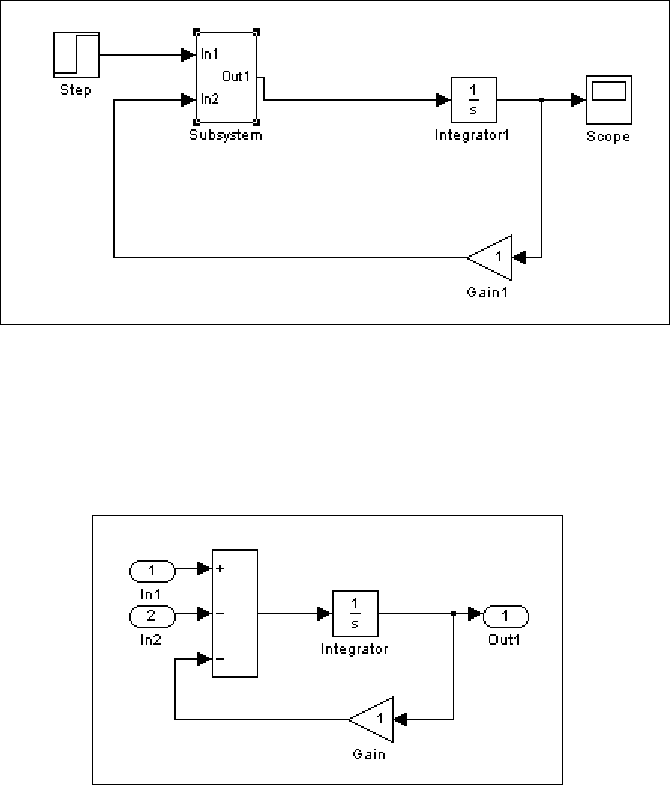
Рис. 7. 87. Создание подсистемы из части блок-схемы (результат)
Если раскрыть окно блока
Subsystem,
дважды щелкнув на нем, то Simulink отобразит блок-схему
созданной подсистемы (рис. 7. 88).
Рис. 7. 88. Созданная подсистема
Как видно, Simulink прибавил блоки
In и Out для отображения входов и выходов в систему высшего
уровня.
7.2.6. Запись и распечатка блок-схемы S-модели
Для записи модели (блок схемы) на диск нужно выполнить команду Save или Save As в меню
File
окна модели.
При этом Simulink записывает в указанную директорию файл с указанным (введенным из клавиатуры)
именем, присваивая нему расширение MDL.
Чтобы распечатать модель (блок-схему) на принтере, достаточно воспользоваться командой Print из меню
File
окна модели.
Довольно интересной является возможность "распечатать" блок-схему в документе любого текстового
редактора, например, Word. Для этого следует использовать команду Copy Model to clipboard из меню
Edit
окна
модели, которая запоминает в буфере содержимое окна модели. Если после этого войти в окно текстового
редактора и нажать клавиши
Shift
+
Insert
, в открытом документе редактора возникнет изображение блок-схемы
модели. Именно таким образом получены рисунки 7. 80...7. 88.
7.3. Примеры создания S-моделей
Рассмотрим несколько примеров составления S-моделей.
7.3.1. Моделирование поведения физического маятника
Рассмотрим процесс построения S-модели на примере задачи моделирования поведения физического маятника
при гармонической вибрации точки его опоры, решенной ранее (урок 2).
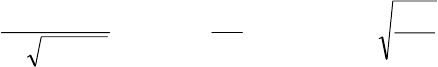
312
Пользуясь результатами ранее проведенных (п. 2.6.2) преобразований, исходное уравнение движения маятника
примем в такой безразмерной форме
),,(sin
ϕϕτϕ
ϕ
′
=+
′′
S
, (7.1)
где обозначено
],sin)sin(cos)sin([
2),,(
ϕετνϕετν
ϕζϕϕτ
⋅+⋅⋅+⋅+⋅⋅−
−
′
⋅⋅−=
′
ymyxmx
nn
S
(7.2 )
причем безразмерные величины
ζ
и определяются выражениями:
ν
Jmgl
R
⋅⋅
=
2
ζ
;
0
ω
ω
ν
=
;
J
mgl
=
0
ω
.
Исходными (задаваемыми) параметрами для моделирования будем считать:
1) параметры самого маятника; к ним в анализируемом случае относятся только относительный
коэффициент затухания
ζ
;
2) параметры, характеризующие внешнее воздействие; сюда входят:
- амплитуды виброперегрузок в вертикальном
my
n
и
горизонтальном
mx
n
направлениях;
- относительная (по отношению к частоте собственных малых колебаний маятника) частота
вибрации точки опоры
;
- начальные фазы
ν
y
ε
и
x
ε
вибрации точки опоры;
3) начальные условия движения маятника:
- начальное отклонение
от вертикали;
- начальная безразмерная угловая скорость маятника
ϕ
o
ωϕ
ϕ
/
&
=
′
.
К выходным (моделируемым) величинам будем относить текущий угол отклонения маятника от вертикали
)(
τ
ϕ
и его безразмерную угловую скорость
)(
τ
ϕ
′
.
Запишем уравнение (7.1) несколько в другой форме:
ϕϕϕτ
ϕ
sin),,( −
′
=
′′
S
. (7.3)
Прежде, чем приступить к составлению S- модели, отметим одну очень важную особенность взаимодействия
рабочего пространства MatLab и среды Simulink.
ВНИМАНИЕ. Все рабочее пространство (WorkSpace) системы MatLab доступно для исполняемых
S-моделей среды Simulink. Поэтому при задании значений настраиваемым
параметрам S-блоков можно вместо конкретных числовых значений вводить имена
переменных (идентификаторы), которые существуют в данный
момент времени в
рабочем пространстве MatLab и даже выражения из них, записанные на М-языке.
Это свойство значительно облегчает составление блок-схем, позволяя вначале формировать массив переменных
в рабочем пространстве, а при составлении блок-схем значения настраиваемых параметров блоков выражать
через эти переменные.
В дальнейшем будем использовать следующие обозначения исходных
и искомых величин в рабочем
пространстве MatLab.
В формулах
В рабочем
пространстве
Примечание
)0(
ϕ
fi0
начальное значение угла отклонения маятника от вертикали
)0(
ϕ
′
fit0
начальная безразмерная угловая скорость маятника
ς
dz
относительный коэффициент затухания
mx
n
nmx
амплитуда виброперегрузки вдоль горизонтальной оси
my
n
nmy
амплитуда виброперегрузки вдоль вертикальной оси
313
ν
nu
относительная частота вибрации тоски подвеса
x
ε
ex
начальная фаза виброперегрузки в горизонтальном направлении
Буд м предпола , что тем или аходятся в
ого уравнения в блок-схему положим такую идею:
y
ε
ey
начальная фаза виброперегрузки в вертикальном направлении
е гать иным способам этим переменным присвоены значения и они н
рабочем пространстве.
В основу воплощения эт
если сформировать правую часть уравнения по «известным» процессам
( )
τ
ϕ
и
),,(
ϕϕτ
′
S
, то тем самым
станет известным угловое ускорение
)(
τ
ϕ
′′
. Если теперь проинтегриро уск жно получить вать орение, мо
угловую скорость
)(
τ
ϕ
′
. Наконец, про рировав и ее, можно получить закон изменения углаинтег
)(
τ
ϕ
от
времени. Последние ченные две величины (процессы) можно теперь использовать для формир ия полу ован
правой части уравнения (7.3).
Итак, для формирования блок-схемы, осуществляющей численное интегрирование уравнения (7.1), можно
поступить так. В основу блок-схемы положить два последовательно соединенных интегратора (блоки
Integrator
); на вход первого интегратора подать угловое ускорение, а как начальное условие использовать
начальное значение угловой скорости
)0(
ϕ
′
; выходом этого блока будет текущая угловая скорость
)(
τ
ϕ
′
; эту
величину следует подать на вход второг егратора с начальным условием в виде начального значе гла
)0(
о инт ния у
ϕ
; выходом этого блока будет искомый процесс
)(
τ
ϕ
.
мим эту часть блок-схемы в виде подсистемы. Д огОфор ля эт о в пустое окно будущей блок-схемы перетянем из
Ports&Subsystem блок
Subsystem и дважды щелкнем на нем. В появившемся окне соберем блок-схему
подсистемы, показанную на рис. 7.89, и назовем ее «Маятник».
Рис. 7. 89. Подсистема «Маятник»
ри настраивании первого блока
Integrator
запишем
fit0
в качестве его параметра Initial condition. Во
й угол отклонения маятника от вертикали
П
втором интеграторе этому параметру присвоим значение
fi0.
Выходными величинами созданной подсистемы являются текущи
ϕ
и его текущая безразмерная угловая скорость
ϕ
′
.
Используя их, можно теперь аналогично сформ рови ать подсистему, вычисляющую текущее значение
вем безразмерного «момента» внешних сил, действующих на маятник при вибрации точки его опоры. Назо
новую подсистему «Внешние моменты сил» (рис. 7. 90).

314
Рис. 7. 90. Подсистема «Внешние моменты сил»
Наглядно видно, что общая структура подсистемы осуществляет действия по формированию выражения (7.2).
Выходной порт ее выдает величину
.
),,(
τϕϕ
′
S
Можно заметить, что величина
dz (относительного коэффициента затухания) использована в блоке Gain
внизу блок-схемы
. Кроме того, при формировании перегрузок по горизонтальной и вертикальной осям
(блоки «Вертик. вибрация» и «Горизонт. вибрация») в параметрах настраивания использованы переменные
nmx, nmy, nu, ex
и
ey
(рис. 7. 91).
315
Рис. 7. 91. Установки в блоке «Горизонт. вибрация»
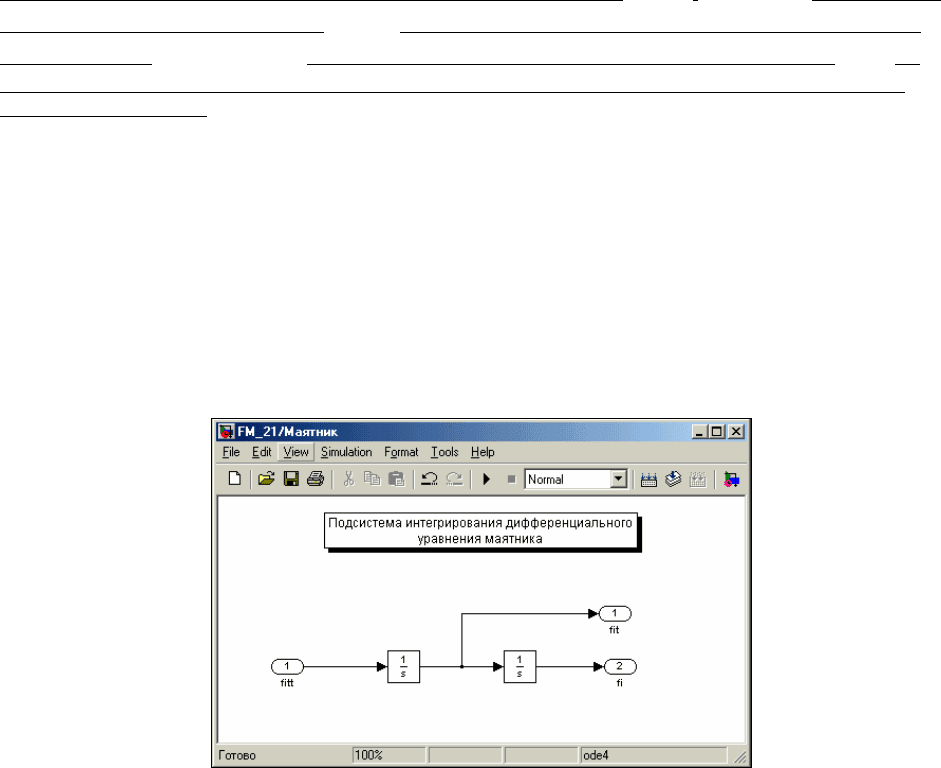
Теперь, используя эти две созданные подсистемы, можно и собрать основную блок-схему, реализующую
уравнение (7.3). Она изображена на рис. 7. 92. Назовем ее «FM_21»
Рис. 7. 92. Основная блок-схема «FM_21»
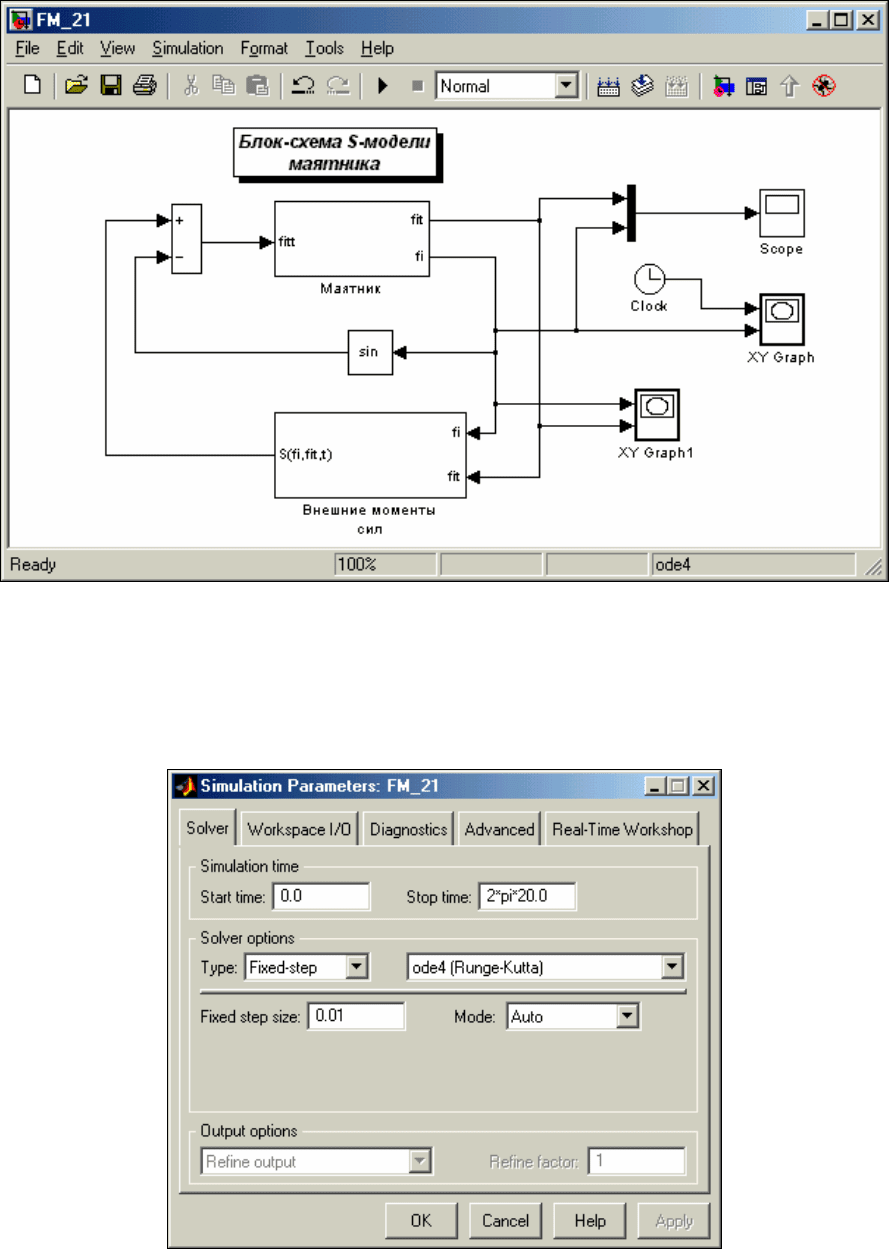
Перед моделированием следует вначале задать параметры численного интегрирования дифференциального
уравнения маятника на вкладке Solver (рис. 7. 93).
316
Рис. 7. 93. Установка параметров численного интегрирования
Установим интервал моделирования ( по безразмерному времени) от Start time=0 до Stop time=2*pi*20, что
соответствует двадцати периодам собственных малых колебаний маятника. Тип решателя (метода
интегрирования) установим с фиксированным шагом (Type= Fixed-step), метод интегрирования – Рунге-Кутта
4-го порядка (ode4) а значение шага интегрирования – 0,01 с (Step size=0.01).
Модель практически готова к моделированию.
Осталось
лишь обеспечить присвоение значений всем переменным, которые были использованы в параметрах
настраивания блоков. Для этого запишем небольшую программу FM_21_dat.m (см. ниже):
% FM_21_dat
% Программа ввода данных для S-модели FM_21
% Лазарев Ю. Ф. 23-01-2004
nmy=1;
nmx=0;
ey=0;
ex=0;
nu=2.3;
dz=0.1;
fi0=160*pi/180;
fit0=0;
Данные, введенные в файле
FM_21_dat.m
соотвествуют чисто вертикальной вибрации основания с
частотой в 2,3 большей частоты собственных незатухающих колебаний маятника с амплитудой по ускорению в
1g и начальному отклонению маятника от вертикаль в 160 градусов.
Запуская вначале программу
FM_21_dat.m
из командного окна MatLab, а затем S-модель FM_21 из окна ее
блок-схемы, получим в обзорных окнах модели результаты, представленные на рис. 7. 94…7.96.
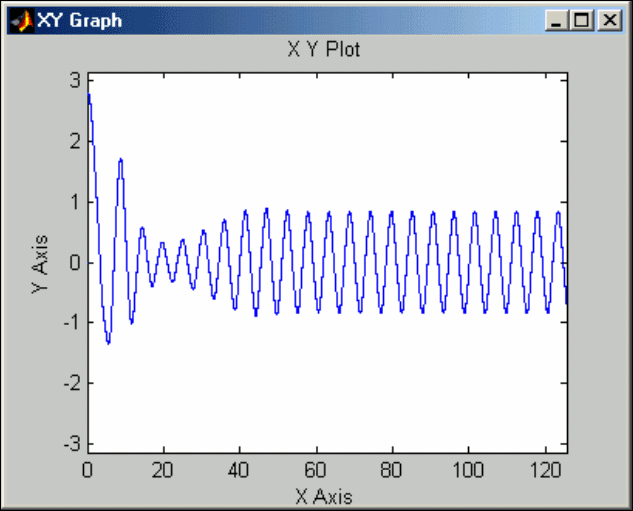
Рис. 7. 94. Результат моделирования, представленный в окне XY Graph
317
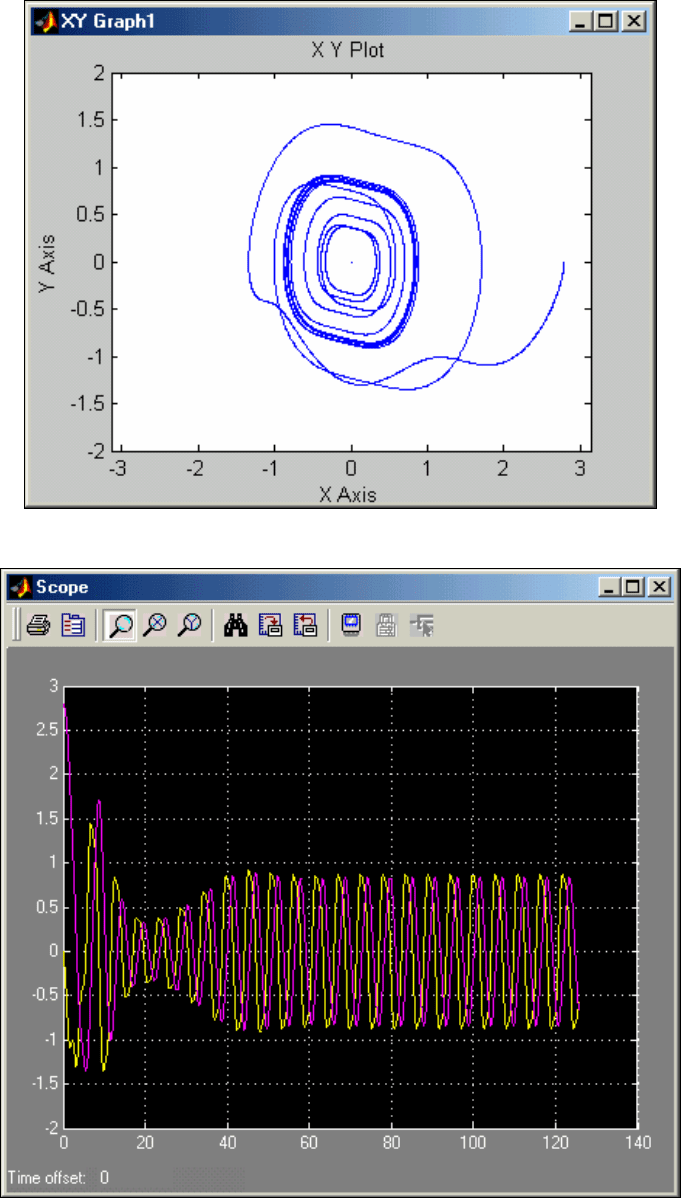
Рис. 7. 95. Результат моделирования, представленный в окне XY Graph1
Рис. 7. 96. Результат моделирования, представленный в окне Scope
В графическом окне блока
XY Graph1 (см. рис. 7. 95) изображен фазовый портрет маятника при выбранных
параметрах маятника и возмущений. В графическом окне блока
Scope представлены (рис. 7. 96) графики
зависимости угла и угловой скорости от времени.
Результаты полностью соответствуют полученным ранее (урок 2) и иллюстрируют возникновение
параметрических колебаний маятника при вертикальной вибрации точки его подвеса.

318
Изменяя данные настройки в файле
FM_21_dat.m
, можно проводить исследования поведения маятника при
произвольных значениях входных параметров.
Из приведенного понятны значительные преимущества и некоторые недостатки моделирования динамических
систем с помощью пакета Simulink в сравнении с аналогичными исследованиями с помощью программы
MatLab:
- составление блок-схемы уравнений движения вместо набора текста процедуры правых
частей значительно более наглядно, позволяет контролировать правильность набора путем
осознания физического содержания отдельных блоков и их взаимосвязей;
- при проведении самого процесса моделирования в среде Simulink исчезает потребность
в организации самого процесса численного интегрирования дифференциальных уравнений
и даже выведения результатов в графической форме;
- однако форма вывода результатов в графической форме в Simulink является
недостаточно гибкой: нельзя добавить собственные надписи в заголовок и по осям графика,
нельзя установить сетку координатных линий в графические окна блоков XY Graph; в
особенности неудобно то, что здесь не предусмотрены средства вывода текстовой
информации на поле графика, что делает графическое представление безадресным.
Последний недостаток существенен. Он может быть устранен существующими в пакете Simulink средствами.
Например, можно записать полученные значения исходных величин в MAT-файл (посылая их на блок
To
File
), а потом создать и использовать программу, которая бы осуществляла считывание данных, записанных в
МАТ-файле, и формирование на этой основе графического изображения в окне фигуры по образцу,
приведенному в разделах 2.5 и 2.7. Такой путь использован в следующем примере. Неудобством применения
обзорного окна
XY Graph является также то, что предварительно нужно установить диапазоны изменения
обеих входных величин по осям графика. Если эти диапазоны установлены неверно, в обзорном окне может
вообще не возникнуть изображение графика, или появится такой его фрагмент, по которому невозможно
сделать правильный вывод о поведении исследуемой системы. А при исследовании системы часто невозможно
заранее предусмотреть диапазоны изменений величин, или сделать это слишком сложно.
7.3.2. Моделирование движения трех гравитирующих тел
Здесь рассматривается классическая задача небесной механики – определение движения трех гравитирующих
материальных точек – с точки зрения численного моделирования его в среде Simulink.
Пусть существуют три изолированные материальные точки с массами соответственно
, и .
Обозначим радиус-векторы этих точек относительно некоторой неподвижной в инерциальном пространстве
точки О через
R
1
m
2
m
3
m
1
, R
2
и
R
3
.
Тогда дифференциальные уравнения движения этих трех точек могут быть записаны в виде:
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
⋅
⋅
⋅+⋅
⋅
⋅−=
⋅
⋅
⋅+⋅
⋅
⋅−=
⋅
⋅
⋅−⋅
⋅
⋅=
;
;
;
13
3
31
13
3
3
32
23
2
3
2
3
32
3
32
32
3
21
21
2
2
2
2
13
3
31
31
3
21
21
2
2
1
RR
R
RR
R
RR
R
2
21
21
1
R
mm
G
R
mm
G
dt
d
m
R
mm
G
R
mm
G
dt
d
m
R
mm
G
R
mm
G
dt
d
m
(7.4)
где обозначено
.
;
2
121
RRR −=
;
233
RRR
2
−=
313
RRR
1
−=
Исследования уравнений движения (и, особенно, численное) всегда удобнее производить по уравнениям в
безразмерном виде, - в этом случае сокращается число параметров, от которых зависит решение.
Приведем уравнения (4) к безразмерной форме. Для этого в качестве базовых используем такие физические
величины:
G
- гравитационная постоянная размерности L
3
M
-1
T
-2
(L – единица длины, M – единица массы, T – единица
времени);
319
1
m
- масса первого тела, которое будем считать основным; им обычно является наиболее массивное тело
(например, Солнце, которое находится под действием гравитационного притяжения Земли (второе, среднее по
массе тело) и Луны (третье, наименее массивное тело)); размерность М;
210
R
- начальное значение расстояния второго тела от первого, размерностью L.
Теперь введем безразмерные величины:
1) безразмерная масса первого тела, очевидно, будет равна единице;
2) безразмерная масса второго тела равна
1
2
2
m
m
=
µ
; (7.5)
3) безразмерная масса третьего тела равна
1
3
3
m
m
=
µ
; (7.6)
4) безразмерные длины радиус-векторов
210
1
1
R
R
=
ρ
;
210
2
2
R
R
=
ρ
;
210
3
3
R
R
=
ρ
: (7.7)
5) безразмерные радиус-векторы
210
R
i
i
R
r =
;
210
R
ij
ij
R
r =
; (7.8)
5) безразмерное время определим формулой
t
R
mG
⋅
⋅
=
3
210
1
τ
; (7.9)
Последняя формула означает, что в качестве единицы измерения времени используется величина
1
3
20
2
mG
R
T
o
⋅
=
π
. (7.10)
В случае, например, Солнца, Земли и Луны эта величина равна году.
Принятое безразмерное время таково, что безразмерный период кругового обращения второго тела вокруг
первого равен
.
π
2
С учетом этого уравнения (4) в безразмерной форме приобретут вид
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
⋅+⋅−=
⋅+⋅−=
⋅−⋅=
13
3
31
3
3
32
2
2
3
2
32
3
32
3
21
3
21
2
2
2
13
3
31
3
21
3
21
2
2
2
1
;
1
;
rr
r
rr
r
rr
r
2
1
ρρ
µ
τ
ρ
µ
ρτ
ρ
µ
ρ
µ
τ
d
d
d
d
d
d
(7.11)
где обозначено
jiij
rrr
−=
;
ijij
r=
ρ
. (7.12)
320
Три вектора (12) связаны между собой соотношением
0
213213
=++ rrr
, (7.13)
Уравнения движения удобнее полностью выразить в векторах (12), характеризующих положение тел
относительно друг друга. Для этого вычтем по очереди уравнения (11) одно из другого. Из полученных трех
уравнений исключим вектор
. Останутся два уравнения
13
r
⎪
⎪
⎩
⎪
⎪
⎨
⎧
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−=
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−=
21
3
31
3
21
3
3
31
3
32
32
2
32
2
32
3
31
3
32
321
3
31
3
3
21
2
2
21
2
111
;
111
rr
r
rr
r
2
ρρρρ
µµ
τ
ρρ
µ
ρ
µ
ρ
µ
τ
d
d
d
d
(7.14)
Эти уравнения и положим в основу моделирования. При этом надо принять во внимание, что
.
1)0(
21
=
ρ
При составлении S-модели будем использовать следующие переменные рабочего пространства:
В формуле В рабочем
пространстве
Примечание
1
2
2
m
m
=
µ
mu2 отношение масс второго и первого тела
1
3
3
m
m
=
µ
mu3 отношение масс третьего и первого тела
)0(),0(),0(
212121
zyx
X210, Y210, Z210 Начальные безразмерные координаты второго тела
относительно первого
)0(),0(),0(
323232
zyx
X320, Y320, Z320 Начальные безразмерные координаты третьего тела
относительно второго
)0(),0(),0(
212121 zyx
VVV
V21x, V21y, V21z Начальные безразмерные проекции вектора скорости
второго тела относительно первого
)0(),0(),0(
323232 zyx
VVV
V32x, V32y, V32z Начальные безразмерные проекции вектора скорости
третьего тела относительно второго
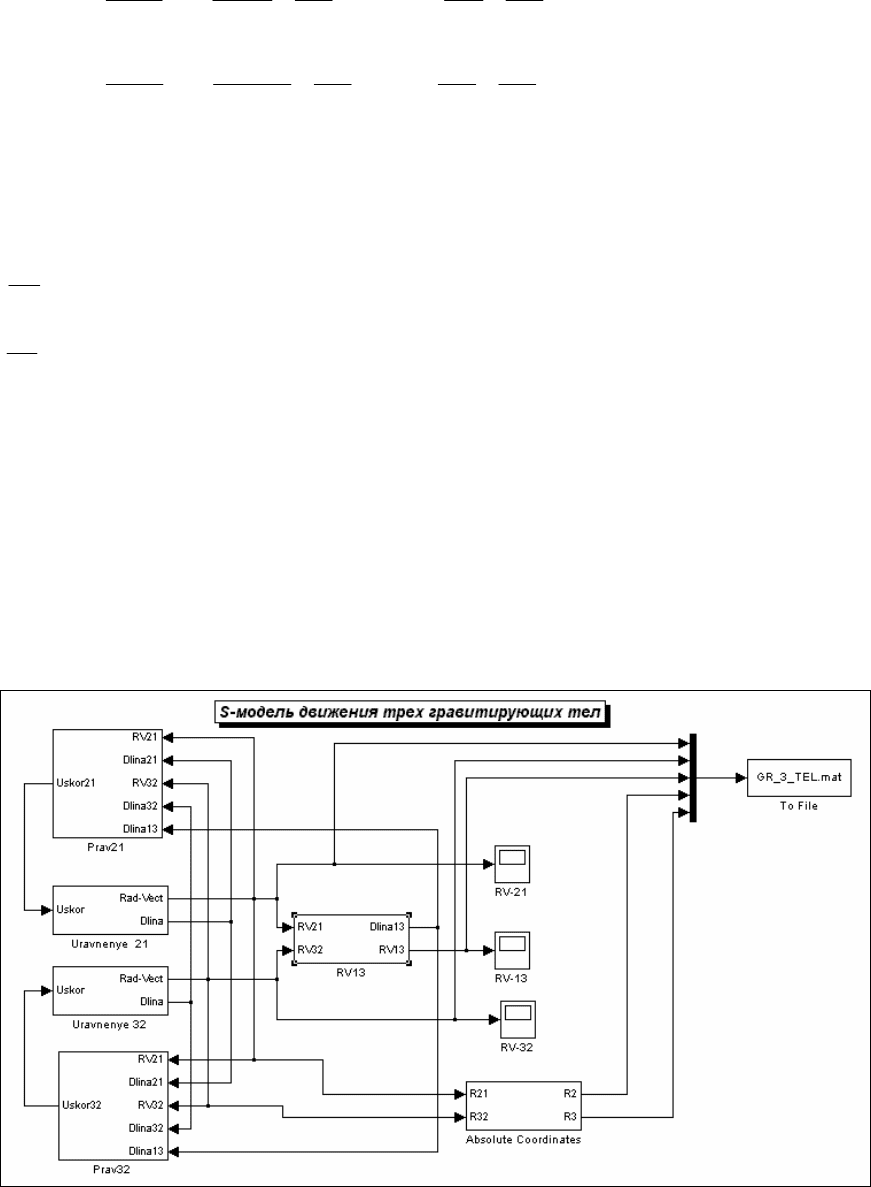
Вариант S-модели под названием
GR_3_TEL. mdl
приведен на рис. 7. 97. Она включает 6 подсистем –
Uravnenye 21, Uravnenye 32, Prav 21, Prav 32, RV13 и Absolute Coordinates и блок To File.
Последний обеспечивает запись результатов моделирования в МАТ-файл под названием GR_3_TEL.mat, в
котором они сохраняются в матрице под именем RV.
Рис. 7. 97. Блок-схема S-модели GR_3_TEL. mdl
