Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II
Подождите немного. Документ загружается.

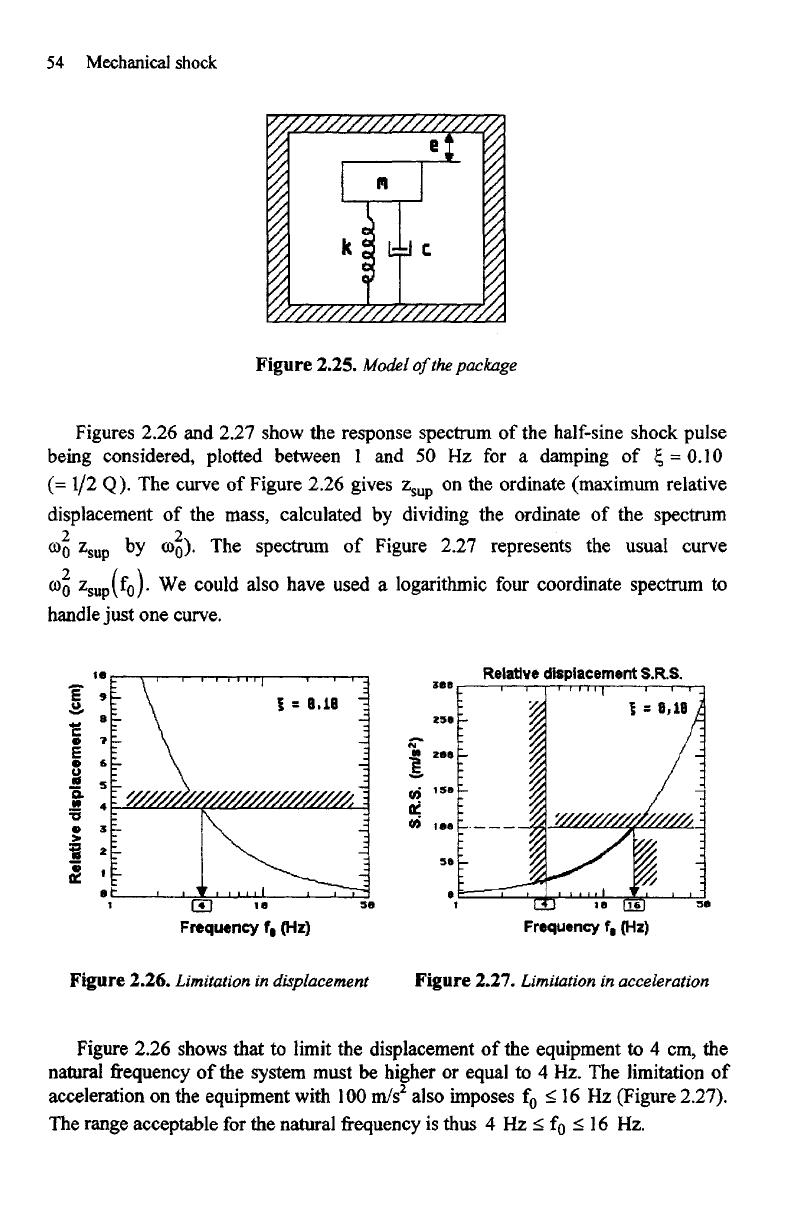
54
Mechanical shock
Figure
2.25.
Model
of
the
package
Figures
2.26
and
2.27 show
the
response spectrum
of the
half-sine
shock pulse
being
considered, plotted between
1 and 50 Hz for a
damping
of £, =
0.10
(= 1/2 Q). The
curve
of
Figure 2.26 gives
z
su
on the
ordinate (maximum relative
displacement
of the
mass, calculated
by
dividing
the
ordinate
of the
spectrum
OD
O
z
sup
by
co
0
).
The
spectrum
of
Figure 2.27 represents
the
usual curve
G)
0
z
sup
(f
0
).
We
could also have used
a
logarithmic
four
coordinate spectrum
to
handle
just
one
curve.
Figure
2.26.
Limitation
in
displacement
Figure 2.27.
Limitation
in
acceleration
Figure
2.26 shows that
to
limit
the
displacement
of the
equipment
to 4 cm, the
natural
frequency of the
system must
be
higher
or
equal
to 4 Hz. The
limitation
of
acceleration
on the
equipment with
100
m/s
2
also imposes
f
0
< 16 Hz
(Figure
2.27).
The
range acceptable
for the
natural
frequency is
thus
4 Hz < f
0
< 16 Hz.

Shock
response
spectra
domains
55
2.10.
Use of
shock
response
spectra
for the
study
of
systems with several
degrees
of
freedom
By
definition,
the
response spectrum gives
the
largest value
of the
response
of a
linear
single-degree-of-freedom system subjected
to a
shock.
If the
real structure
is
comparable
to
such
a
system,
the SRS can be
used
to
evaluate this response directly.
This approximation
is
often
possible, with
the
displacement response being mainly
due
to the first
mode.
In
general, however,
the
structure comprises several modes
which
are
simultaneously excited
by the
shock.
The
response
of the
structure
consists
of the
algebraic
sum of the
responses
of
each excited mode.
One
can
read
on the SRS the
maximum response
of
each
one of
these
modes,
but
one
does
not
have
any
information concerning
the
moment
of
occurrence
of
these
maxima.
The
phase relationships between
the
various modes
are not
preserved
and
the
exact
way in
which
the
modes
are
combined cannot
be
known simply.
In
addition,
the SRS is
plotted
for a
given constant damping over
all the
frequency
range,
whereas this damping varies
from one
mode
to
another
in the
structure. With
rigour,
it
thus appears
difficult
to use a SRS to
evaluate
the
response
of a
system
presenting more than
one
mode.
But it
happens that this
is the
only possible means.
The
problem
is
then
to
know
how to
combine these 'elementary' responses
so as to
obtain
the
total response
and to
determine,
if
need
be, any
suitable participation
factors
dependent
on the
distribution
of the
masses
of the
structure,
of the
shapes
of
the
modes etc.
Let
us
consider
a
non-linear system
with
n
degrees
of freedom; its
response
to a
shock
can be
written
as:
Knowing
that
we
deduce that

56
Mechanical shock
where
n
=
total number
of
modes
a
n
=
modal participation factor
for the
mode
n
h
n
(t)=
impulse response
of
mode
n
x(t)
=
excitation (shock)
(j)
-
modal vector
of
the
system
a =
variable
of
integration
If
one
mode
(m) is
dominant, this relation
is
simplified
according
to
The
value
of the SRS to the
mode
m is
equal
to
The
maximum
of the
response z(t)
in
this particular case
is
thus
When
there
are
several
modes,
several
proposals
have been made
to
limit
the
value
of the
total
response
of the
mass
j of the one of the
degrees
of freedom
starting
from the
values read
on the SRS as
follows.
A
first
method
was
proposed
in
1934
per H.
Benioff
[BEN 34], consisting
simply
of
adding
the
values with
the
maxima
of the
responses
of
each mode, without regard
to
the
phase.
A
very conservative value
was
suggested
by
M.A. Biot [BIO
41] in
1941
for the
prediction
of the
responses
of
buildings
to
earthquakes, equal
to the sum of the
absolute
values
of the
maximum
modal responses:

Shock response
spectra
domains
57
The
result
was
considered
sufficiently
precise
for
this application [RID 69].
As it is
not
very probable that
the
values
of the
maximum responses take place
all at the
same moment with
the
same sign,
the
real
maximum
response
is
lower than
the sum
of
the
absolute values. This method gives
an
upper limit
of the
response
and
thus
has
a
practical advantage:
the
errors
are
always
on the
side
of
safety.
However,
it
sometimes leads
to
excessive safety factors [SHE 66].
In
1958,
S.
Rubin [RUB
58]
made
a
study
of
undamped two-degrees-of-freedom
systems
in
order
to
compare
the
maximum responses
to a
half-sine shock calculated
by the
method
of
modal superposition
and the
real maximum responses. This tsudy
showed
that
one
could obtain
an
upper limit
of the
maximum response
of the
structure
by a
summation
of the
maximum
responses
of
each
mode
and
that,
in the
majority
of the
practical problems,
the
distribution
of the
modal
frequencies and the
shape
of the
excitation
are
such that
the
possible error remains probably lower than
10%.
The
errors
are
largest when
the
modal
frequencies are in
different
areas
of the
SRS,
for
example,
if a
mode
is in the
impulse domain
and the
other
in the
static
domain.
If
the
fundamental
frequency of the
structure
is
sufficiently
high, Y.C. Fung
and
M.V.
Barton [FUN
58]
considered that
a
better approximation
of the
response
is
obtained
by
making
the
algebraic
sum of the
maximum
responses
of the
individual
modes:
Clough
proposed
in
1955,
in the
study
of
earthquakes, either
to add to the
response
of the first
mode
a fixed
percentage
of the
responses
of the
other modes,
or
to
increase
the
response
of the
first
mode
by a
constant percentage.
The
problem
can be
approached
differently
starting
from an
idea drawn
from
probability theory. Although
the
values
of the
response
peaks
of
each individual
mode
taking place
at
different
instants
of
time cannot,
in a
strict sense, being treated
in
purely
statistical
terms, Rosenblueth suggested combining
the
responses
of the
modes
by
taking
the
square root
of the sum of the
squares
to
obtain
an
estimate
of
the
most probable value [MER 62].
This
criterion, used again
in
1965
by
F.E. Ostrem
and
M.L. Rumerman [OST
65]
in
1955 [RID 69], gives values
of the
total response lower than
the sum of the
absolute values
and
provides
a
more realistic evaluation
of the
average conditions.
This
idea
can be
improved
by
considering
the
average
of the sum of the
absolute
values
and the
square root
of the sum of the
squares (JEN 1958).
One can
also
choose
to
define
positive
and
negative limiting values starting
from a
system
of

58
Mechanical shock
weighted averages.
For
example,
the
relative displacement response
of the
mass
j is
estimated
by
where
the
terms
are the
absolute values
of the
maximum responses
of
each
mode
and p is a
weighting factor [MER 62].

Chapter
3
Characteristics
of
shock response spectra
3.1.
Shock response spectra domains
Three domains
can be
schematically distinguished
in
shock spectra:
- An
impulse
domain
at low
frequencies,
in
which
the
amplitude
of the
spectrum
(and thus
of the
response)
is
lower than
the
amplitude
of the
shock.
The
shock here
is
of
very short duration with respect
to the
natural period
of the
system.
The
system
reduces
the
effects
of the
shock.
The
characteristics
of the
spectra
in
this domain will
be
detailed
in
Section 3.2.
- A
static domain
in the
range
of the
high
frequencies,
where
the
positive
spectrum
tends
towards
the
amplitude
of the
shock whatever
the
damping.
All
occurs
here
as if the
excitation
were
a
static
acceleration
(or a
very slowly varying
acceleration),
the
natural period
of the
system being small compared with
the
duration
of the
shock.
This
does
not
apply
to
rectangular
shocks
or to the
shocks
with
zero rise time.
The
real shocks having necessarily
a
rise time
different
from
zero,
this
restriction
remains
theoretical.
- An
intermediate domain,
in
which there
is
dynamic amplification
of the
effects
of the
shock,
the
natural period
of the
system being close
to the
duration
of the
shock. This amplification, more
or
less
significant
depending
on the
shape
of the
shock
and the
damping
of the
system,
does
not
exceed 1.77
for
shocks
of
traditional
simple
shape (half-sine, versed-sine, terminal peak
saw
tooth (TPS)). Much larger
values
are
reached
in the
case
of
oscillatory shocks, made
up, for
example,
by a few
periods
of a
sinusoid.

TTTTT
3.2. Characteristics
of
shock response spectra
at low
frequencies
3.2.1. General characteristics
In
this impulse region
- The
form
of the
shock
has
little influence
on the
amplitude
of
the
spectrum.
We
will
see
below that only (for
a
given damping)
the
velocity change
AV
associated
with
the
shock, equal
to the
algebraic
surface under
the
curve
x(t),
is
important.
-The
positive
and
negative spectra
are in
general
the
residual
spectra
(it is
necessary sometimes that
the
frequency
of
spectrum
is
very small,
and
there
can be
exceptions
for
certain long shocks
in
particular). They
are
nearly symmetrical
so
long
as
damping
is
small.
2
-The
response
(pseudo-acceleration
co
0
z
sup
or
absolute acceleration
y
sup
)
is
lower
than
the
amplitude
of the
excitation. There
is an
'attenuation'.
It is
thus
in
this
impulse
region that
it
would
be
advisable
to
choose
the
natural frequency
of an
isolation
system
to the
shock,
from
which
we can
deduce
the
stiffness
envisaged
of
the
insulating material:
(with
m
being
the
mass
of the
material
to be
protected).
- The
curvature
of the
spectrum always cancels
at the
origin
(f
0
= 0 Hz)
[FUN
57].
The
characteristics
of the SRS are
often
better demonstrated
by a
logarithmic
chart
or a
four
coordinate representation.
3.2.2.
Shocks
with
velocity
changed
from zero
For
the
shocks simple
in
shaoe
,
the
residual spectrum
is
larger than
the
primary spectrum
at low
frequencies.
For an
arbitrary damping
£ it can be
shown that
the
impulse response
is
given
by
where
z(t)
is
maximum
for t
such
as
0,
i.e.
fort such that
echanical shock

Characteristics
of
shock
response
spectra
61
The
tangent
at the
origin
of the
spectrum plotted
for
zero damping
in
linear
scales
has a
slope proportional
to the
velocity
change AVcorresponding
to the
shock
pulse.
If
damping
is
small, this relation
is
approximate.
yielding
The SRS is
thus equal
at low
frequencies
to
sin(arctan
i.e.
1
and the
slope tends towards
AV. The
slope
p of the
spectrum
at the
origin
is
then equal
to:
62
Mechanical shock
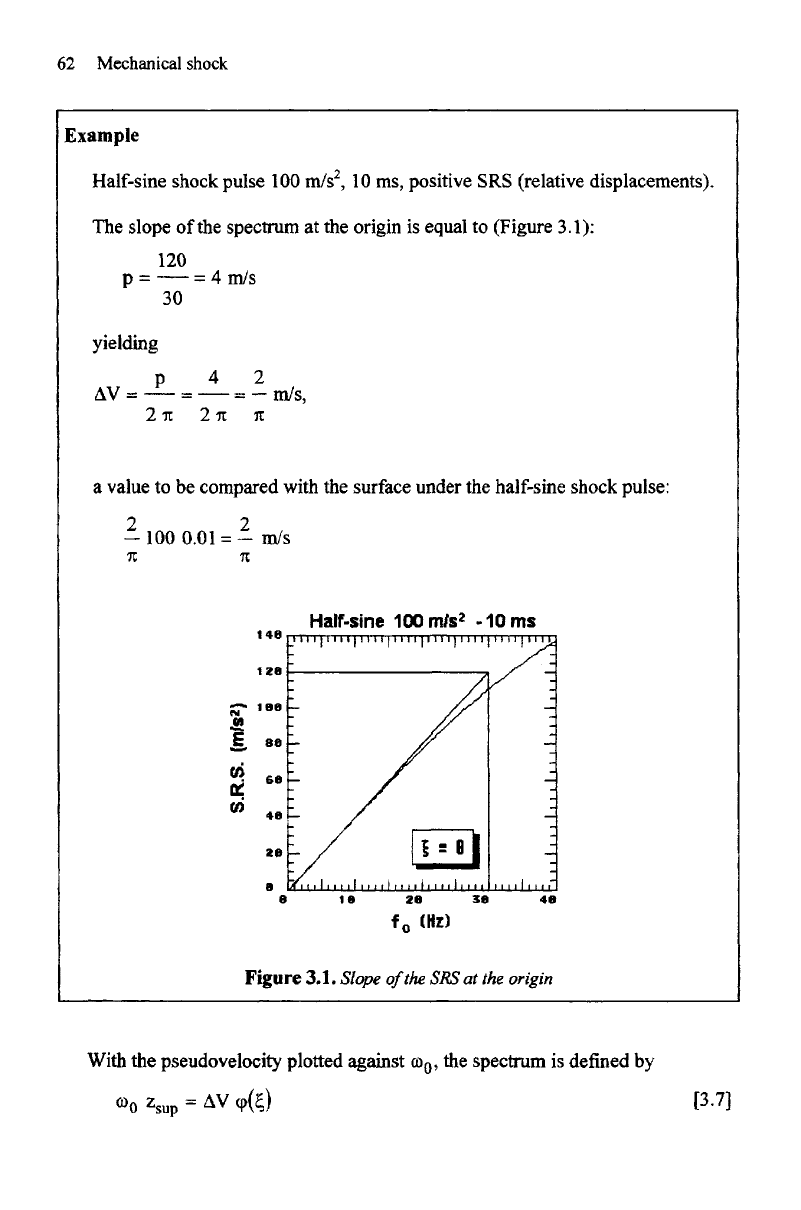
Example
Half-sine
shock pulse
100
m/s
2
,
10 ms,
positive
SRS
(relative displacements).
The
slope
of the
spectrum
at the
origin
is
equal
to
(Figure 3.1):
a
value
to be
compared with
the
surface under
the
half-sine shock pulse:
Figure
3.1. Slope
of
the
SRS at the
origin
With
the
pseudovelocity plotted
against
to
0
,
the
spectrum
is
defined
by
yielding
Characteristics
of
shock
response
spectra
63
When
O>Q
tends towards zero,
co
0
z
sup
tends towards
the
constant value
AV
cp(^).
Figure
3.2
shows
the
variations
of
cp(^)
versus
£.
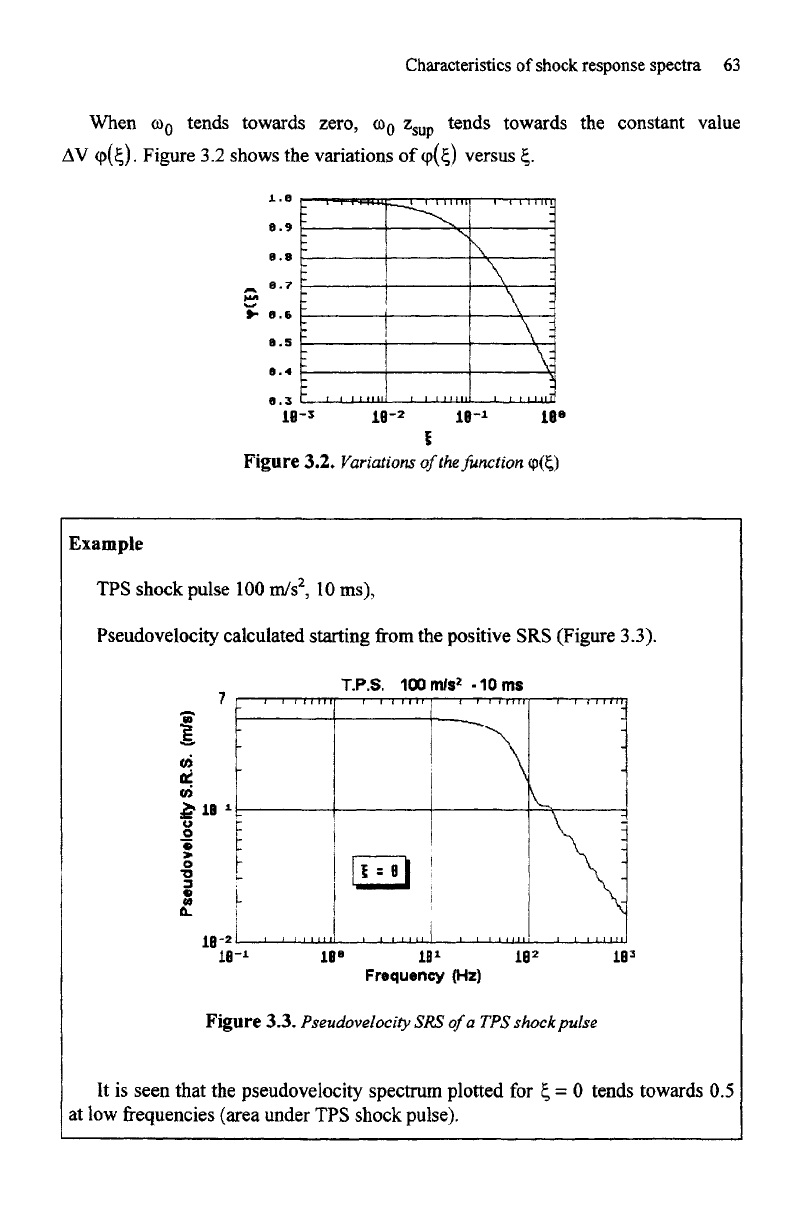
Example
IPS
shock pulse
100
m/s
2
,
10
ms),
Pseudovelocity calculated starting
from the
positive
SRS
(Figure 3.3).
Figure
3.3.
Pseudovelocity
SRS
of
a
TPS
shock
pulse
It
is
seen that
the
pseudovelocity spectrum plotted
for £ = 0
tends towards
0.5
at
low frequencies
(area
under
TPS
shock
pulse).
Figure
3.2.
Variations
of
the
function
<p(£)
