Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II
Подождите немного. Документ загружается.


24
Mechanical shock
difficult
to
carry
out if one
used
a
fine
model
of the
structure,
and
besides this
is not
always
available,
in
particular
at the
stage
of the
development
of the
specification
of
dimensioning.
One
searches
for a
method
of
general nature, which leads
to
results
which
can be
extrapolated
to any
structure.
A
solution
was
proposed
by
M.A. Biot [BIO
32] in
1932
in a
thesis
on the
study
of the
earthquakes
effects
on the
buildings; this study
was
then generalized
to
analysis
of all
kinds
of
shocks.
The
study consists
of
applying
the
shock
under
consideration
to a
'standard'
mechanical
system, which thus does
not
claim
to be a
model
of the
real structure,
composed
of a
support
and of N
linear one-degree-of-freedom resonators,
comprising
each
one a
mass
m
i
, a
spring
of
stiffness
kj and a
damping device
Cj,
chosen such that
the fraction of
critical damping
is
the
same
for all N
resonators (Figure 2.1).
Figure
2.1.
Model
of
the
shock
response
spectrum
(SRS)
When
the
support
is
subjected
to the
shock, each mass
nij has a
specific
movement
response according
to its
natural
frequency
chosen
damping
£,
while
a
stress
GJ is
induced
in the
elastic element.
and
to the
The
analysis consists
of
seeking
the
largest stress
cr
mj
observed
at
each
frequency
in
each spring.
A
shock
A is
regarded
as
more severe than
a
shock
B if it
induces
in
each resonator
a
larger extreme
stress.
One
then carries
out an
extrapolation, which
is
certainly
criticizable,
by
supposing that,
if
shock
A is
more
severe than shock
B
when
it is
applied
to all the
standard resonators,
it is
also more

Shock
response
spectra
domains
25
severe
with
respect
to an
arbitrary
real
structure
(which
cannot
be
linear
nor
having
a
single
degree
of freedom).
NOTE:
A
study
was
carried
out in
1984
on a
mechanical assembly composed
of
a
circular
plate
on
which
one
could
place
some masses
and
thus vary
the
number
of
degrees
of freedom. The
stresses generated
by
several shocks
of
the
same spectra
(in
the frequency
range including
the
principal resonance
frequencies), but of
different
shapes [DEW 84], were measured
and
compared.
One
noted that
for
this
assembly
whatever
the
number
of
degrees
of
freedom,
—
two
pulses
of
simple form (with
no
velocity change) having
the
same spectrum
induce
similar stresses,
the
variation
not
exceeding approximately
20 %. It is the
same
for two
oscillatory shocks;
—
the
relationship between
the
stresses measured
for a
simple shock
and an
oscillatory
shock
can
reach
2.
These
results were supplemented
by
numerical simulation intended
to
evaluate
the
influence
ofnon linearity. Even
for
very strong non-linearity,
one did not
note
for the
cases considered,
an
important
difference
between
the
stresses induced
by
two
shocks
of
the
same spectrum,
but
of
different
form.
A
complementary
study
was
carried
out by
B.B. Petersen [PET
81] in
order
to
compare
the
stresses directly deduced
from a
shock response spectrum with those
generated
on an
electronics component
by a
half-sine
shock envelop
of a
shock
measured
in the
environment
and by a
shock
of the
same spectrum made
up from
WA
VSIN
signals
(Chapter
9)
added with various delays.
The
variation between
the
maximum responses measured
at
five points
in the
equipment
and the
stresses
calculated starting
from the
shock response spectra does
not
exceed
a
factor
of
3 in
spite
of the
important theoretical
differences
between
the
model
of the
response
spectrum
and the
real structure studied.
For
applications
deviating
from the
assumptions
of
definition
of the
shock
response
spectrum
(linearity, only
one
degree
of freedom), it is
desirable
to
observe
a
certain
prudence
if one
wishes
to
estimate
quantitatively
the
response
of a
system
starting
from the
spectrum [BOR 89].
The
response
spectra
are
more
often
used
to
compare
the
severity
of
several
shocks.
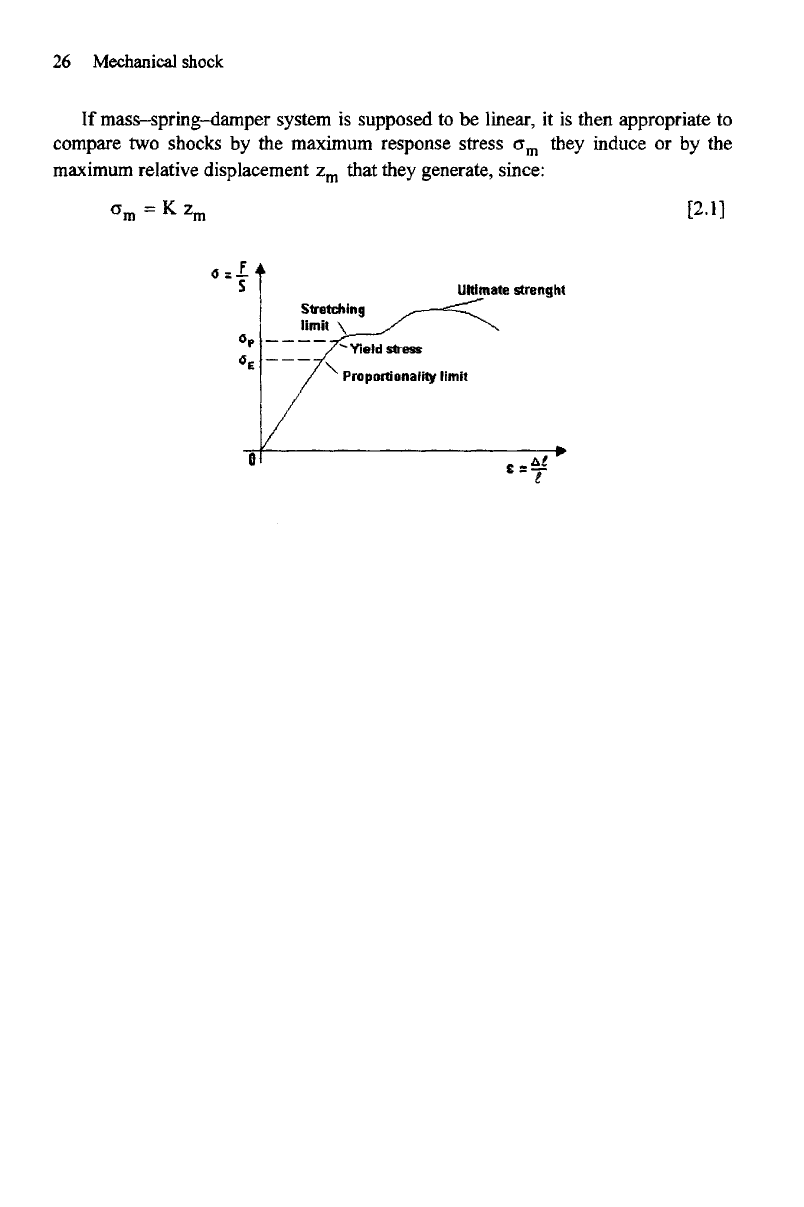
It
is
known that
the
tension
static
diagram
of
many materials comprises
a
more
or
less linear
arc on
which
the
stress
is
proportional
to the
deformation.
In
dynamics,
this proportionality
can be
allowed within
certain
limits
for the
peaks
of the
deformation
(Figure 2.2).
26
Mechanical shock
If
mass-spring-damper
system
is
supposed
to be
linear,
it is
then appropriate
to
compare
two
shocks
by the
maximum response stress
a
m
they induce
or by the
maximum
relative displacement
z
m
that they generate, since:
Figure 2.2.
Stress-strain
curve
z
m
is a
function only
of the
dynamic properties
of the
system, whereas
a
m
is
also
a
function,
via K, of the
properties
of the
materials which constitute
it.
The
curve giving
the
largest relative displacement
z
sup
multiplied
by oo
0
according
to the
natural
frequency f
0
, for a
given
£
damping,
is the
shock response
spectrum
(SRS).
The first
work defining
these
spectra
was
published
in
1933
and
1934
[BIO
33]
[BIO 34], then
in
1941
and
1943 [BIO
41]
[BIO 43].
The
shock
response
spectrum,
then named
the
shock spectrum,
was
presented
there
in the
current
form.
This spectrum
was
used
in the
field
of
environmental
tests
from
1940
to
1950:
J.M. Frankland [FRA
42] in
1942, J.P. Walsh
and
R.E. Blake
in
1948 [WAL 48],
R.E. Mindlin [MIN 45]. Since then, there have beenmany works which used
it as
tool
of
analysis
and for
simulation
of
shocks
[HIE 74], [KEL 69], [MAR
87] and
[MAT
77].
2.2.
Response
of a
linear
one-degree-of-freedom
system
2.2.1.
Shock
defined
by a
force
Being given
a
mass-spring-damping
system subjected
to a
force F(t) applied
to
the
mass,
the
differential
equation
of the
movement
is
written
as:

Shock response
spectra
domains
27
Figure
2.3. Linear
one-degree-of-freedom
system
subjected
to a
force
where z(t)
is the
relative displacement
of the
mass
m
relative
to the
support
in
response
to the
shock F(t). This equation
can be put in the
form:
where
(damping factor)
and
(natural
pulsation).
2.2.2.
Shock
defined
by an
acceleration
Let
us set as
x(t)
an
acceleration
applied
to the
base
of a
linear
one-degree-of-
freedom
mechanical system, with y(t)
the
absolute acceleration response
of the
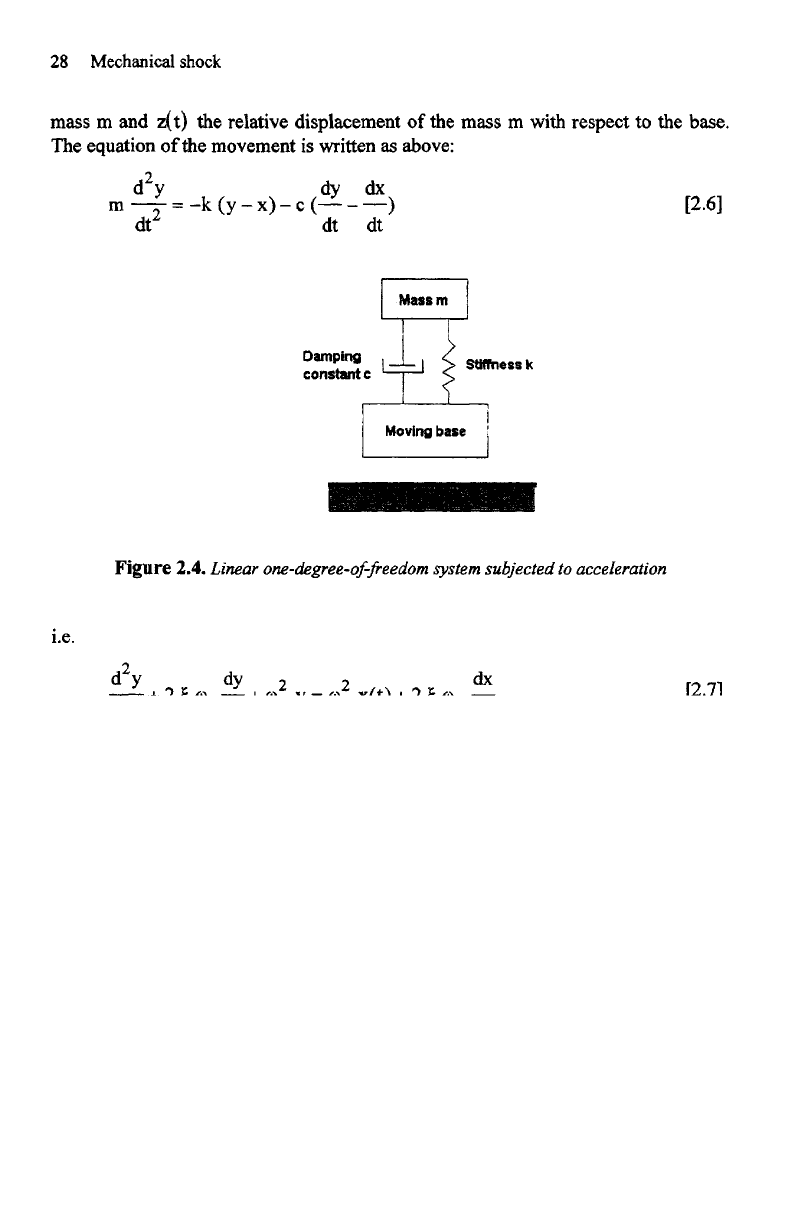
28
Mechanical
shock
mass
m and
z(t)
the
relative
displacement
of the
mass
m
with
respect
to the
base.
The
equation
of the
movement
is
written
as
above:
Figure 2.4.
Linear
one-degree-of-freedom
system
subjected
to
acceleration
i.e.
or,
while
setting z(t)
=
y(t)
-
x(t):
2.2.3.
Generalization
Comparison
of the
differential
equations [2.3]
and
[2.8] shows that they
are
both
of the
form
where
/(t)
and
u(t)
are
generalized
functions
of the
excitation
and
response.

Shock response spectra domains
29
NOTE:
The
generalized equation [2.9]
can be
-written
in the
reduced
form:
where
£
m
=
maximum
of
l(t)
Resolution
The
differential
equation
[2.10]
can be
integrated
by
parts
or by
using
the
Laplace transformation.
We
obtain,
for
zero initial conditions,
an
integral called
Duhamel
's
integral:
where
variable
of
integration.
In the
generalized
form,
we
deduce that
where
a is an
integration variable homogeneous with time.
If the
excitation
is an
acceleration
of the
support,
the
response
relative displacement
is
given
by:
and
the
absolute acceleration
of the
mass
by:
30
Mechanical shock
Application
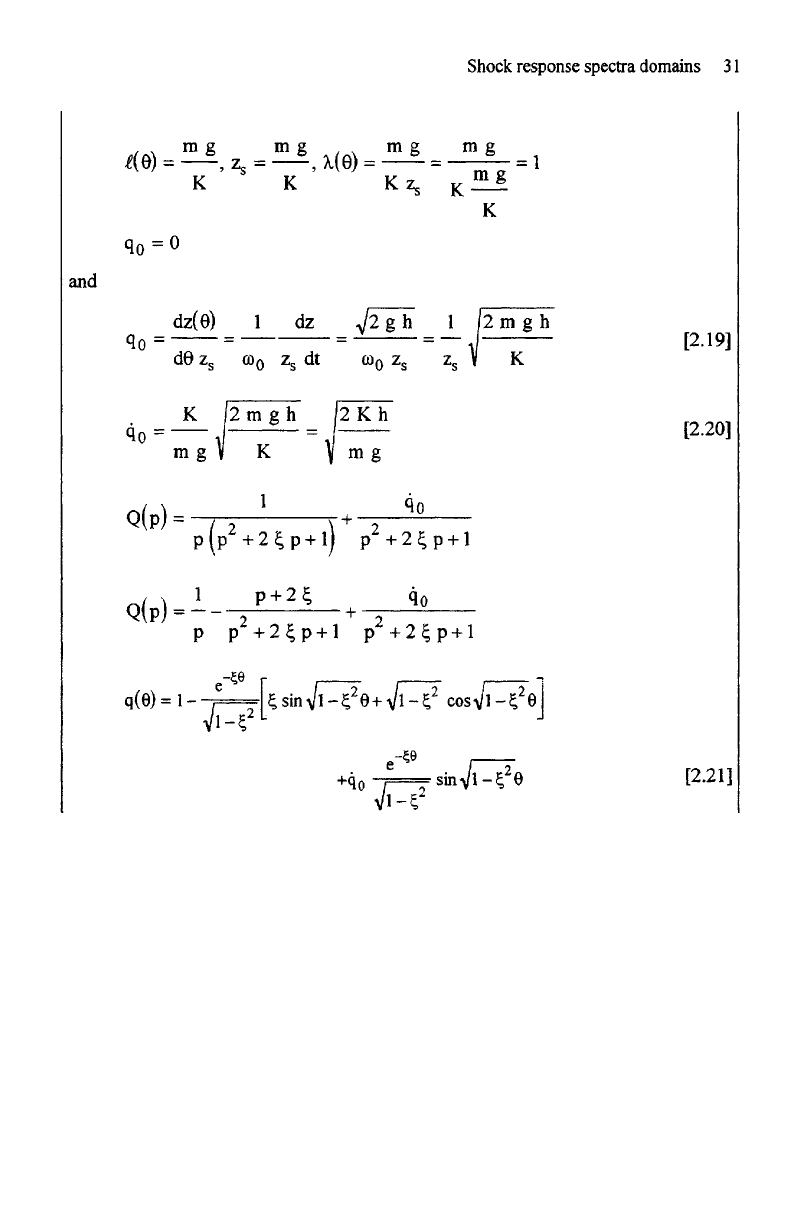
Let
us
consider
a
package intended
to
protect
a
material
from
mass
m and
comprising
a
suspension made
up of two
elastic elements
of
stiffness
k and two
dampers
of
damping
constant
c.
Figure
2.5.
Model
of
the
package
Figure
2.6. Equivalent model
We
want
to
determine
the
movement
of the
mass
m
after
free
fall
from a
height
of
h = 5 m, by
supposing that there
is no
rebound
of the
package
after
the
impact
on
the
ground
and
that
the
external
frame is not
deformable (Figure 2.5). This
system
is
equivalent
to the
model
in
Figure 2.6.
We
have (Volume
1,
Chapter
3):
and
Shock response
spectra
domains
31

32
Mechanical shock
where
and
With
the
chosen numerical values,
it
becomes:

Shock
response
spectra
domains
33
From
this
it is
easy
to
deduce
the
velocity z(t)
and the
acceleration z(t)
from
successive derivations
of
this expression.
The
first
term corresponds
to the
static
deformation
of the
suspension under load
of 100 kg.
2.2.4.
Response
of
a
one-degree-of-freedom
system
to
simple
shocks
Half-sine
pulse
Versed-sine
pulse
