Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II
Подождите немного. Документ загружается.

14
Mechanical shock
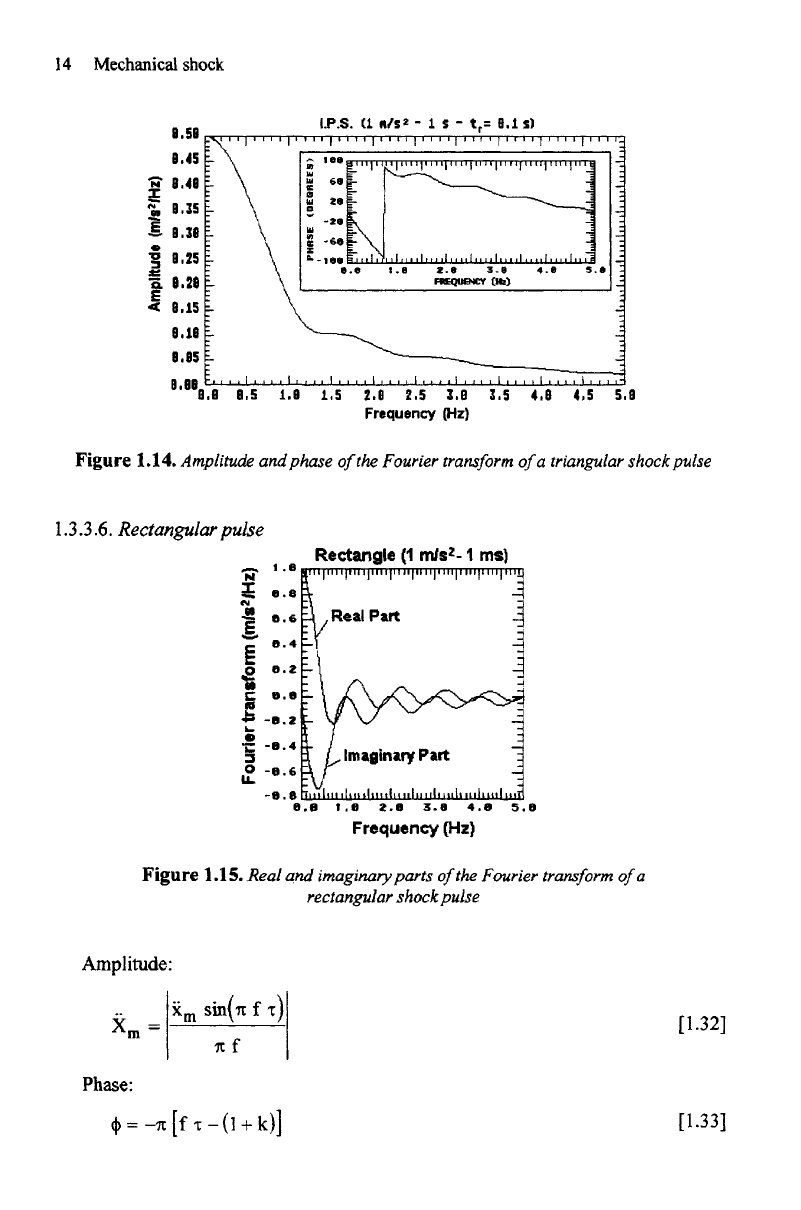
Figure
1.14.
Amplitude
and
phase
of
the
Fourier
transform
of
a
triangular shock pulse
1.3.3.6.
Rectangular pulse
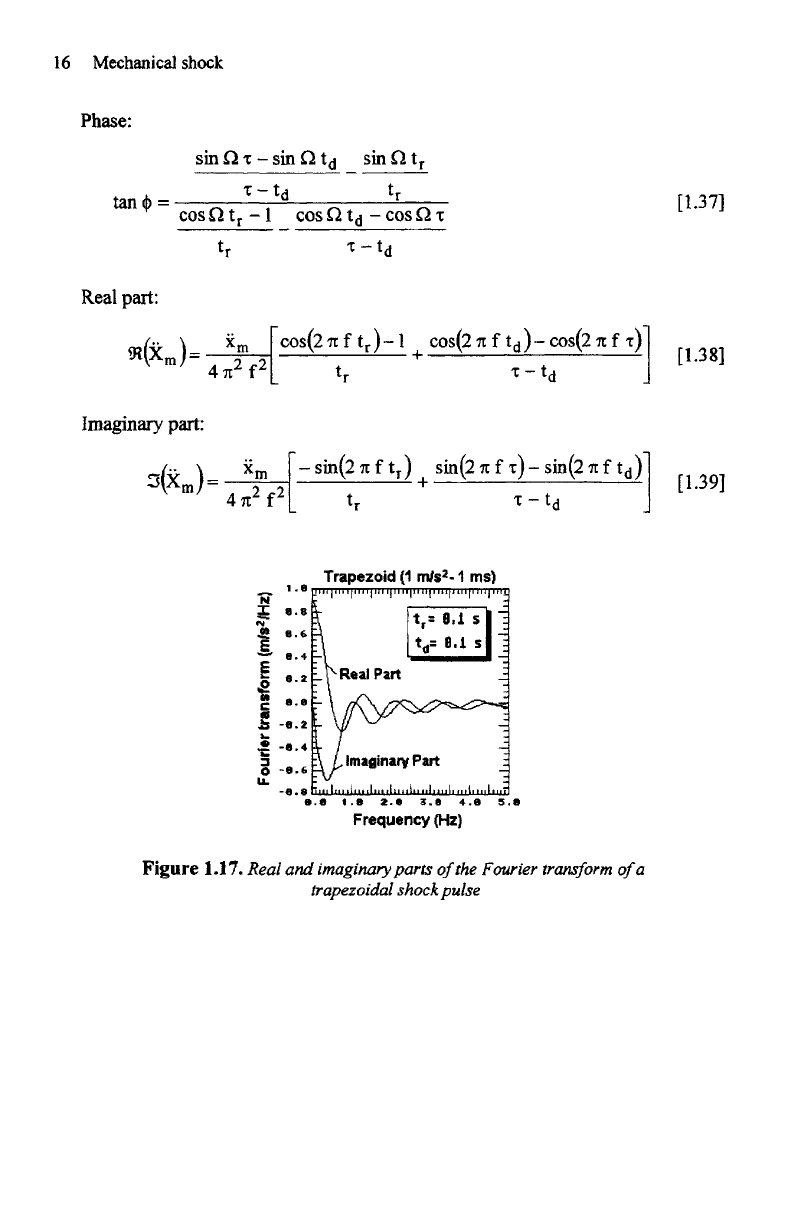
Figure 1.15.
Real
and
imaginary parts
of
the
Fourier
transform
of
a
rectangular shock pulse
Amplitude:
Phase:

Real
part:
Imaginary
part:
Shock analysis
15
Figure
1.16.
Amplitude
and
phase
of
the
Fourier
transform
of
a
rectangular shock pulse
1.3.3.7.
Trapezoidal
pulse
Amplitude:
16
Mechanical shock
Phase:
Real
part:
Imaginary
part:
Figure
1.17.
Real
and
imaginary
parts
of
the
Fourier
transform
of
a
trapezoidal
shock pulse

Shock
analysis
17
Figure
1.18.
Amplitude
and
phase
of
the
Fourier
transform
of
a
trapezoidal
shock
pulse
1.3.4. Importance
of
the
Fourier
transform
The
Fourier spectrum contains
all the
information
present
in the
original signal,
in
contrast,
we
will see,
to the
shock response spectrum
(SRS).
It
is
shown that
the
Fourier spectrum R(Q)
of the
response
at a
point
in a
structure
is the
product
of the
Fourier spectrum X(Q)
of the
input
shock
and the
transfer
function H(Q)
of the
structure:
R(Q)
=
H(Q) X(Q) [1-40]
The
Fourier spectrum
can
thus
be
used
to
study
the
transmission
of a
shock
through
a
structure,
the
movement resulting
at a
certain point being then described
by
its
Fourier spectrum.
The
response
in the
time domain
can be
also
expressed
from
a
convolution utilizing
the
'input'
shock signal according
to the
time
and the
impulse
response
of the
mechanical system considered.
An
important property
is
used here:
the
Fourier transform
of a
convolution
is
equal
to the
scalar product
of the
Fourier
transforms
of the two
functions
in the
frequency
domain.
It
could
be
thought that this (relative)
facility
of
change
in
domain (time
<=>
frequency) and
this convenient description
of the
input
or of the
response would
make
the
Fourier spectrum method
one frequently
used
in the
study
of
shock,
in
particular
for the
writing
of
test
specifications
from
experimental data.
These mathematical advantages, however,
are
seldom used within this
framework,
because
when
one
wants
to
compare
two
excitations,
one
runs
up
against
the
following problems:

18
Mechanical
shock
- The
need
to
compare
two
functions.
The
Fourier variable
is a
complex quantity
which
thus requires
two
parameters
for its
complete description:
the
real part
and the
imaginary part (according
to the frequency) or the
amplitude
and the
phase. These
curves
in
general
are
very little smoothed and, except
in
obvious
cases,
it is
difficult
to
decide
on the
relative severity
of two
shocks
according
to frequency
when
the
spectrum overlap.
In
addition,
the
phase
and the
real
and
imaginary parts
can
take
positive
and
negative values
and are
thus
not
very easy
to use to
establish
a
specification;
- The
signal obtained
by
inverse transformation
has in
general
a
complex
form
impossible
to
reproduce with
the
usual test facilities, except, with certain limitations,
on
electrodynamic shakers.
The
Fourier transform
is
used neither
for the
development
of
specifications
nor
for
the
comparison
of
shocks.
On the
other hand,
the
one-to-one relation property
and
the
input-response relation [1.40] make
it a
very interesting tool
to
control
shaker shock whilst calculating
the
electric signal
by
applying these means
to
reproduce
with
the
specimen
a
given acceleration profile,
after
taking into account
the
transfer
function
of the
installation.
1.4.
Practical calculations
of the
Fourier transform
1.4.1.
General
Among
the
various possibilities
of
calculation
of the
Fourier transform,
the
Fast
Fourier
Transform
(FFT) algorithm
of
Cooley-Tukey
[COO
65] is
generally used
because
of its
speed (Volume
3). It
must
be
noted that
the
result issuing
from
this
algorithm must
be
multiplied
by the
duration
of the
analysed signal
to
obtain
the
Fourier transform.
1.4.2.
Case: signal
not yet
digitized
Let us
consider
an
acceleration time history x(t)
of
duration
T
which
one
wishes
to
calculate
the
Fourier transform with
n
FT
points (power
of 2)
until
the frequency
f
max
.
According
to the
Shannon's theorem (Volume
3), it is
enough that
the
signal
is
sampled with
a frequency
f
samp
= 2
f
max
,
i.e. that
the
temporal step
is
equal
to
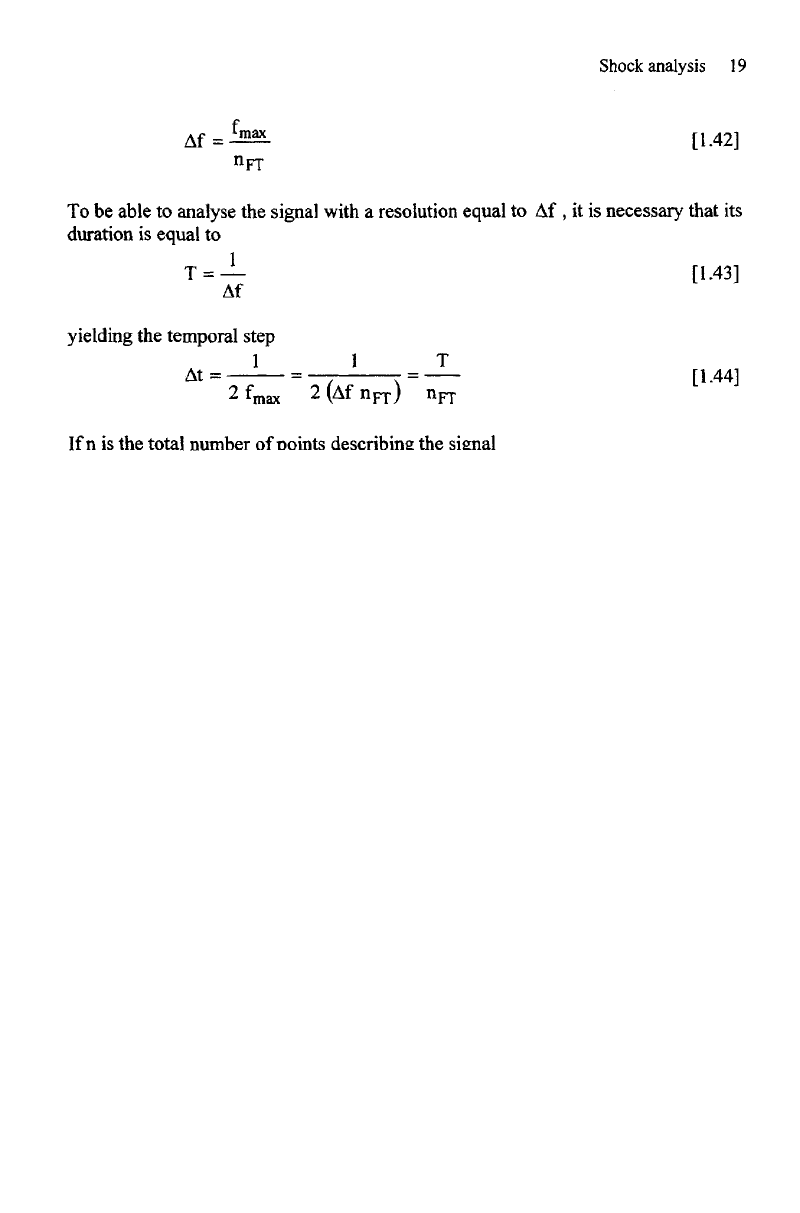
The frequency
interval
is
equal
to
Shock
analysis
19
To be
able
to
analyse
the
signal with
a
resolution equal
to Af , it is
necessary that
its
duration
is
equal
to
yielding
the
temporal step
If
n is the
total number
of
points describing
the
signal
and
one
must have
yielding
The
duration
T
needed
to be
able
to
calculate
the
Fourier transform with
the
selected
conditions
can be
different
to the
duration
T from the
signal
to
analyse (for example
in
the
case
of a
shock).
It
cannot
be
smaller than
T (if not
shock shape would
be
modified).
Thus,
if we set
the
condition
T
leads
to
i.e.
to
If
the
calculation data (n
FT
and
f
max
)
lead
to a too
large value
of Af , it
will
be
necessary
to
modify
one of
these
two
parameters
to
satisfy
to the
above condition.
If
it is
necessary that
the
duration
T is
larger than
T,
zeros must
be
added
to the
signal
to
analyse between
T and T,
with
the
temporal step
At.
The
computing process
is
summarized
in
Table 1.1.

20
Mechanical shock
Table
1.1.
Computing
process
of
a
Fourier
transform
starting
from a
non-digitized
signal
Data:
-
Characteristics
of the
signal
to be
analysed (shape, amplitude, duration)
or
one
measured signal
not yet
digitized.
- The
number
of
points
of
the
Fourier transform (npj-)
and its
maximum
frequency
(f
max
).
Condition
to
avoid
the
aliasing phenomenon (Shannon's
T
samp.
-
fmax
theorem)
. If the
measured signal
can
contain components
at
frequencies
higher than
f
max
,
it
must
be filtered
using
a
low-pass
filter
before digitalization.
To
take account
of the
slope
of the
filter
beyond
f
max
,
it is
preferable
to
choose
fsamp
= 2.6
f
max
(Volume
3).
At
=
Temporal step
of the
signal
to be
digitized (time interval
2
f
max
between
two
points
of the
signal).
fmax
Frequency interval between
two
successive points
of the
At
=
Fourier transform.
n
FT
n
= 2 npr
Number
of
points
of the
signal
to be
digitized.
T = n At
Total duration
of the
signal
to be
treated.
If
T > t,
zeros must added between
T and T.
If
there
are not
enough points
to
represent correctly
the
signal between
0 and T,
fmax
must
t>
e
increased.
f 1
The
condition
Af = -^L < -
must
be
satisfied
(i.e.
T >
T
):
"FT
T
- if
f
max
is
imposed, take
npj
(power
of 2) > T
f
max
.
npr
- if n
FT
is
imposed,
choose
f
max
<
——
.
T
1.4.3.
Case: signal
already
digitized
If
the
signal
of
duration
T
were already digitized with
N
points
and a
step
5T, the
calculation conditions
of the
transform
are fixed:

(nearest power
of 2)
and
(which
can
thus result
in not
using
the
totality
of the
signal).
If
however
we
want
to
choose
a
priori
f
max
and
npj,
the
signal must
be
resampled
and if
required zeros must
be
added using
the
principles
in
Table 1.1.
Shock
analysis
21
This page intentionally left blank

Chapter
2
Shock
response spectra domains
2.1.
Main
principles
A
shock
is an
excitation
of
short duration which induces transitory dynamic
stress structures. These stresses
are a
function
of:
- the
characteristics
of
the
shock (amplitude, duration
and
form);
- the
dynamic properties
of
the
structure (resonance frequencies,
Q
factors).
The
severity
of a
shock
can
thus
be
estimated only according
to the
characteristics
of the
system which undergoes
it. The
evaluation
of
this severity
requires
in
addition
the
knowledge
of the
mechanism leading
to a
degradation
of the
structure.
The two
most common mechanisms are:
- The
exceeding
of a
value threshold
of
the
stress
in a
mechanical part, leading
to
either
a
permanent deformation (acceptable
or
not)
or a
fracture,
or at any
rate,
a
functional
failure.
-
If
the
shock
is
repeated many times (e.g. shock
recorded
on the
landing
gear
of
an
aircraft,
operation
of an
electromechanical
contactor,
etc),
the
fatigue damage
accumulated
in the
structural elements
can
lead
in the
long term
to fracture. We
will
deal with this
aspect
later
on.
The
severity
of a
shock
can be
evaluated
by
calculating
the
stresses
on a
mathematical
or
finite
element model
of the
structure and,
for
example, comparison
with
the
ultimate
stress
of the
material. This
is the
method used
to
dimension
the
structure.
Generally, however,
the
problem
is
rather
to
evaluate
the
relative severity
of
several
shocks
(shocks measured
in the
real environment, measured shocks with
respect
to
standards, establishment
of a
specification etc). This comparison would
be
