Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II
Подождите немного. Документ загружается.


74
Mechanical shock
If
the
velocity change
and the
variation
in
displacement
are
zero
the end of the
shock,
but if the
integral
of the
displacement
has a non
zero value
AD, the
undamped
residual spectrum
is
given
by
[SMA
85]
Figure
3.15.
Residual positive
SRS
of
a
half-sine
pulse
with
half-sine
pre-
and
post-shocks
3.2.5.
Notes
on
residual
spectrum
Spectrum
of
absolute
displacements
When
co
0
is
sufficiently
small,
the
residual spectrum
of an
excitation x(t)
is
identical
to the
corresponding displacement spectrum
in one of the
following
ways
[FUN
61]:
However,
contrary
to the
case
(c)
above,
if
a)
b)
c)
for
small values
of
co
0
(slope
of 18
dB/octave).
Example

Characteristics
of
shock response
spectra
75
but
if
there
exists
more than
one
value
t_ of
time
in the
interval
0
the
spectrum
of the
displacements
is
equal
to the
largest values
of
[FUN
61].
If
AV and AD are
zero
at the end of the
shock,
the
response spectrum
of the
absolute
displacement
is
equal
to 2
x(t) where x(t)
is the
residual displacement
of
the
base.
If
x(t)
= 0, the
spectrum
is
equal
to the
largest
of the two
quantities
input
shock
is
such that
AV * 0.
Relative
displacement
When
(00 is
sufficiently
small,
the
residual spectrum
and the
spectrum
of the
displacements
are
identical
in the
following
cases:
a)
if
X(T)
* 0 at the end of the
shock,
b) if
X(T)
= 0, but
x(t)
is
maximum with
t =
T
.
If
not,
the
residual spectrum
is
equal
to
X(T), while
the
spectrum
of the
displacements
is
equal
to the
largest absolute value
of
x(t).
3.3. Characteristics
of
shock response spectra
at
high frequencies
The
response
can be
written, according
to the
relation [2.16]
which
x(t)
dt = 0,
then
the
residual spectrum
is
equal
to
while
is
cancelled.
The
absolute displacement
of
response
is not
limited
if the
where
t = t
p
is the
time when
the
integral
while
setting
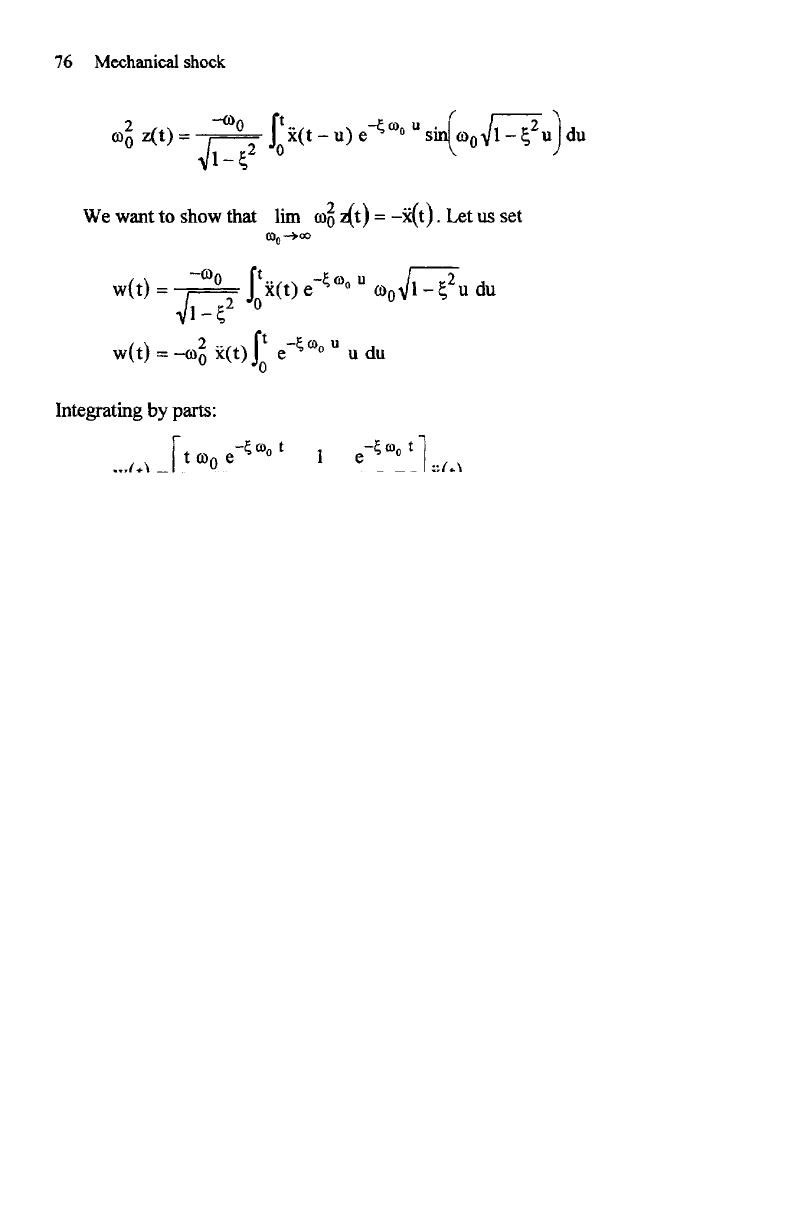
76
Mechanical shock
We
want
to
show that
Let
us set
Integrating
by
parts:
w(t)
tends towards
when
co
0
tends towards
infinity.
Let us
show that
such
that
.
constant.
If
the
function
x(t)
is
continuous,
the
quantity

Characteristics
of
shock response spectra
77
tends towards zero
as u
tends towards zero. There thus
exists
r\ e [o, t]
such that
The
function
x(t)
is
continuous
and
therefore limited
at
Thus
for
At
high
frequencies, o>
0
z(t) thus tends towards x(t) and, consequently,
the
shock
response spectrum tends towards
x
m
, a
maximum x(t).
3.4. Damping
influence
Damping
has
little influence
in the
static region. Whatever
its
value,
the
spectrum tends towards
the
amplitude
of the
signal depending
on
time. This property
is
checked
for all the
shapes
of
shocks, except
for the
rectangular theoretical shock
when,
for
, and we
have
and we
have

78
Mechanical shock
which, according
to
damping, tends towards
a
value ranging between
one and
twice
the
amplitude
of the
shock.
In
the
impulse domain
and
especially
in the
intermediate domain,
the
spectrum
has
a
lower amplitude when
the
clamping
is
greater.
This
phenomenon
is not
great
for
shocks
with velocity change
and for
normal damping (0.01
to 0.1
approximately).
It
is
marked more
for
oscillatory type shocks (decaying sine
for
example)
at
frequencies
close
to the frequency of the
signal.
The
peak
of the
spectrum here
has
an
amplitude which
is a
function
of the
number
of
alternations
of the
signal
and of
the
selected
damping.
3.5.
Choice
of
damping
The
choice
of
damping should
be
carried
out
according
to the
structure subjected
to the
shock
under
consideration.
When this
is not
known,
or
studies
are
being
carried
out
with
a
view
to
comparison with other already calculated
spectra,
the
outcome
is
that
one
plots
the
shock response spectra with
a
relative damping equal
to
0.05 (i.e.
Q =
10).
It is
about
an
average value
for the
majority
of
structures.
Unless otherwise specified,
as
noted
on the
curve,
it is the
value chosen
conventionally. With
the
spectra
varying relatively little with damping (with
the
reservations
of the
preceding paragraph), this choice
is
often
not
very important.
To
limit
possible errors,
the
selected value should, however,
be
systematically noted
on
the
diagram.
NOTE.
In
practice,
the
most
frequent range
of
variation
of
the Q
factor
of
the
structures
lies
between
approximately
5 and 50.
There
is no
exact relation which makes
it
possible
to
obtain
a
shock response spectrum
of
given
Q
factor starting from
a
spectrum
of
the
same signal calculated with another
Q
factor.
M.B.
Grath
and
W.F. Bangs [GRA
72]
proposed
an
empirical method deduced
from an
analysis
of
spectra
of
pyrotechnic shocks
to
carry
out
this
transformation.
It
is
based
on
curves giving, depending
on Q, a
correction factor, amplitude ratio
of
the
spectrum
for Q
factor with
the
value
of
this spectrum
for Q = 10
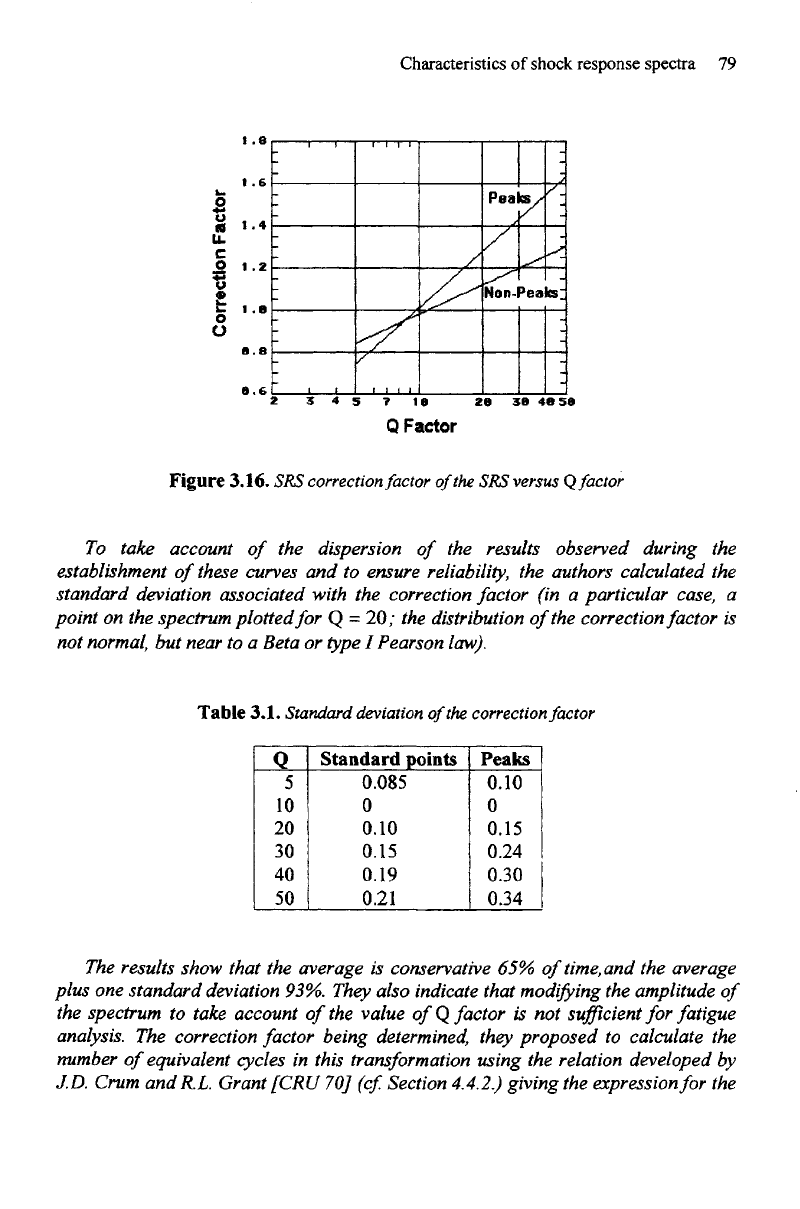
(Figure
3.16).
The
first curve relates
to the
peak
of the
spectrum,
the
second
the
standard point
(non-peak
data).
The
comparison
of
these
two
curves
confirms
the
greatest
sensitivity
of
the
peak
to the
choice
ofQ
factor.
These
results
are
compatible with those
of a
similar
study
carried
out by
W.P.
Rader
and
W.F. Bangs [RAD 70],which
did not
however distinguish between
the
peaks
and the
other values.
Characteristics
of
shock
response
spectra
79
Figure
3.16.
SRS
correction
factor
of
the
SRS
versus
Q
factor
To
take account
of the
dispersion
of the
results observed during
the
establishment
of
these curves
and to
ensure reliability,
the
authors calculated
the
standard deviation associated
-with
the
correction factor
(in a
particular case,
a
point
on the
spectrum
plotted
for Q = 20; the
distribution
of
the
correction factor
is
not
normal,
but
near
to a
Beta
or
type
I
Pearson law).
Table
3.1.
Standard deviation
of
the
correction
factor
The
results show that
the
average
is
conservative
65% of
time,and
the
average
plus
one
standard deviation 93%.
They
also indicate that
modifying
the
amplitude
of
the
spectrum
to
take account
of the
value
of Q
factor
is not
sufficient
for
fatigue
analysis.
The
correction factor being determined,
they
proposed
to
calculate
the
number
of
equivalent cycles
in
this
transformation
using
the
relation developed
by
J.D.
Crum
and
R.L. Grant [CRU
70]
(cf.
Section 4.4.2.) giving
the
expression
for the
Q
5
10
20
30
40
50
Standard
points
0.085
0
0.10
0.15
0.19
0.21
Peaks
0.10
0
0.15
0.24
0.30
0.34

80
Mechanical
shock
response
(OQ
z(t) depending
on the
time during
its
establishment under
a
sine wave
excitation
as:
(where
N =
number
of
cycles
carried
out at
time
t).
Figure
3.17.
SRS
correction factor versus
Q
factor
This
relation, standardized
by
dividing
it by the
amount obtained
for the
particular case where
Q = 10, is
used
to
plot
the
curves
of
Figure 3.17 which make
it
possible
to
readN,
for a
correction factor
and
given
Q.
They
are not
reliable
for
Q < 10, the
relation [3.23] being correct
only
for low
damping.
3.6. Choice
of
frequency range
It
is
customary
to
choose
as the
frequency range:
-
either
the
interval
in
which
the
resonance
frequencies of the
structure studied
are
likely
to be found;
-or the
range
including
the
important
frequencies
contained
in the
shock
(in
particular
in the
case
of
pyrotechnic
shocks).

Characteristics
of
shock
response
spectra
81
Figure
3.18. Four coordinate diagram
3.8. Relation
of
shock response spectrum
to
Fourier spectrum
3.8.1. Primary shock response spectrum
and
Fourier
transform
The
response u(t)
of a
linear undamped one-degree-of-freedom system
to a
generalized excitation ^(t)
is
written [LAL
75]
(Volume
1,
Chapter
2):
3.7. Charts
There
are two
spectral charts:
-
representation
(x, y), the
showing value
of the
spectrum versus
the frequency
(linear
or
logarithmic
scales);
-the
four
coordinate nomographic representation
(four
coordinate spectrum).
pseudovelocity
co
0
z
m
and,
at two
axes
at 45° to the two
first,
the
maximum relative
displacement
z
m
and the
pseudo-acceleration
co
0
z
m
.
This representation
is
interesting
for it
makes
it
possible
to
directly read
the
amplitude
of the
shock
at the
high
frequencies
and,
at low frequencies, the
velocity change
associated
with
the
shock
(or if AV = 0 the
displacement).
One
notes here
on the
abscissae
the frequency
on
the
ordinates
the

82
Mechanical shock
We
suppose
here
that
t is
lower than
T.
where
the
index
P
indicates that
it is
about
the
primary spectrum. However, where
the
Fourier transform
of
£(t),
calculated
as if the
shock were non-zero only between
times
0 and t
with
co
0
the
pulsation
is
written
as
and
has as an
amplitude under
the
following conditions:
which
expression
is of the
form
with
where
C and S are
functions
of
time
t.
u(t)
can be
still written:
with
The
function
is
at a
maximum when
its
derivative
is
zero
This yields
the
maximum absolute
value
of
u(t)

Characteristics
of
shock
response
spectra
83
Comparison
of the
expressions
of
shows
that
In
a
system
of
dimensionless coordinates, with
The
primary spectrum
of
shock
is
thus identical
to the
amplitude
of
the
reduced
Fourier
spectrum,
calculated
for t < T [CA V
64].
The
phase
<|>
L
of the
Fourier spectrum
is
such that
However,
the
phase
<j>
p
is
given
by
[3.28]
where
k is a
positive
integer
or
zero.
For
an
undamped system,
the
primary positive shock spectrum
and the
Fourier
spectrum
between
0 and t are
thus related
in
phase
and
amplitude.
3.8.2. Residual shock response spectrum
and
Fourier
transform
The
response
can be
written, whatever value
of t
