Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II

84

Mechanical

shock

which

is of the

form

B1 sin

co

0

t

+ B

2

cos

<o

0

t

with

B1 and B

2

being

constants.

We

also have

where

the

constant

C is

equal

to

and the

phase

<f>

R

is

such that

The

residual spectrum, expressed

in

terms

of

displacement,

is

thus given

by the

maximum

value

of the

response:

The

Fourier transform

of the

excitation l(i)

is by

definition equal

to:

or

since outside

(0, T), the

function t(t)

is

zero

71 71

Only

the

values

of

<j>

L

€

(-—,+

—)

will

be

considered. Comparison

of

<j)

R

and

(|>

L

2 2

show

that

This expression

can be

written,

by

expressing

the

exponential function according

to

a

sine

and a

cosine term

as,

where R(n)

is the

real part

of the

Fourier integral

and

I(Q)

the

imaginary part.

L(Q)

is a

complex quantity whose module

is

given

by

Let

us

compare

the

expressions

of

D

R

(Q)

and of

|L(Q)|.

Apart

from the

factor

w

0

and

provided that

one

changes

O

0

into

Q,

these

two

quantities

are

identical.

The

natural

frequency of the

system

o>

0

can

take

an

arbitrary value

since

the

simple

mechanical system

is not yet

chosen, equal

in

particular

to Q. We

thus obtain

the

relation

The

phase

is

given

by

For

an

undamped system,

the

Fourier spectrum

and the

residual positive shock

spectrum

are

amplitude

and

phase

[CA V

64].

NOTE:

If

the

excitation

is an

acceleration,

and

if,

in

addition,

the

Fourier

transform

of x

(t),

we

have [GER 66],

[NAS

65]:

Characteristics

of

shock

response

spectra

85

86

Mechanical shock

3.8.3.

Comparison

of

the

relative severity

of

several shocks using their Fourier

spectra

and

their shock response spectra

Let

us

consider

the

Fourier

spectra

(amplitude)

of two

shocks,

one

being

an

isosceles triangle shape

and the

other

TPS

(Figure

3.19),

like their positive shock

response

spectra,

for

zero

damping (Figure

3.20).

yielding

with

V

R

(oo)

being

the

pseudovelocity spectrum.

The

dimension

of

|L(p)|

is

that

of the

variable

of

excitation

^t)

multiplied

by

time.

The

quantity

Q

|L(Q)|

is

thus that

of

l(i).

If the

expression

of

l{t)

is

standardized

by

dividing

it by its

maximum value

l

m

, it

becomes,

in

dimensionless

form

With

this representation,

the

Fourier spectrum

of the

signal

identical

to its

residual shock spectrum

for

zero

damping [SUT 68].

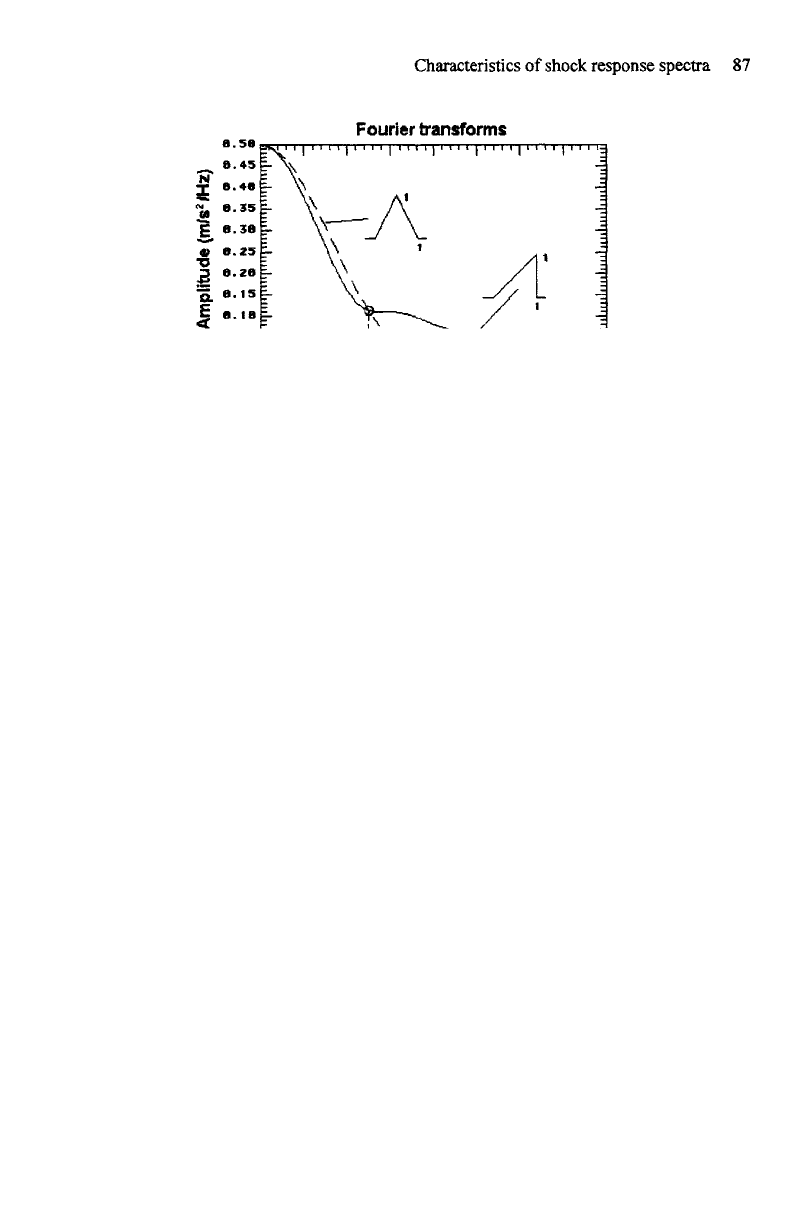
Characteristics

of

shock

response

spectra

87

Figure 3.20.

Comparison

of

the

positive

SRS

of

a

TPS

pulse

and

an

isosceles triangle pulse

It

is

noted that

the

Fourier

spectra

and

shock

response

spectra

of the two

impulses

have

the

same relative position

as

long

as the frequency

remains lower than

f

=1.25

Hz, the

range

for

which

the

shock response spectrum

is

none other than

the

residual spectrum, directly related

to the

Fourier spectrum.

On

the

contrary,

for f >

1.25

Hz, the TPS

pulse

has a

larger Fourier spectrum,

whereas

the SRS

(primary spectrum)

of the

isosceles triangle pulse

is

always

in the

form

of the

envelope.

Figure

3.19.

Comparison

of

the

Fourier

transform

amplitudes

of

a

TPS

pulse

and

an

isosceles triangle pulse

88

Mechanical shock

The

Fourier spectrum thus gives only

one

partial image

of the

severity

of a

shock

by

considering

only

its

effects

after

the end of the

shock (and without taking

damping

into account).

3.9. Characteristics

of

shocks

of

pyrotechnic origin

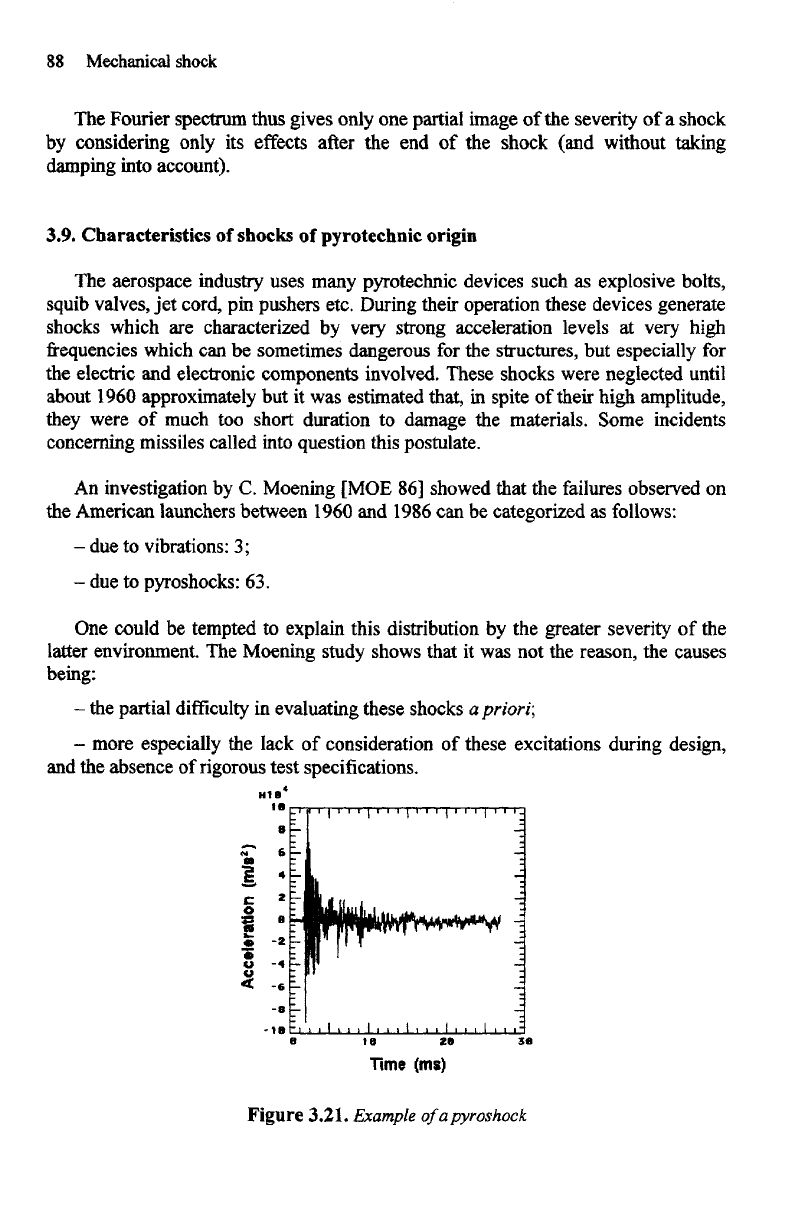
The

aerospace industry uses many pyrotechnic devices such

as

explosive bolts,

squib valves,

jet

cord,

pushers etc. During their operation these devices generate

shocks which

are

characterized

by

very strong

acceleration

levels

at

very high

frequencies

which

can be

sometimes dangerous

for the

structures,

but

especially

for

the

electric

and

electronic

components

involved. These shocks were neglected until

about 1960 approximately

but it was

estimated that,

in

spite

of

their high amplitude,

they

were

of

much

too

short duration

to

damage

the

materials. Some incidents

concerning missiles called

into

question

this

postulate.

An

investigation

by C.

Moening [MOE

86]

showed that

the

failures

observed

on

the

American launchers between 1960

and

1986

can be

categorized

as

follows:

-

due

to

vibrations:

3;

-

due

to

pyroshocks:

63.

One

could

be

tempted

to

explain this distribution

by the

greater severity

of the

latter

environment.

The

Moening study shows that

it was not the

reason,

the

causes

being:

- the

partial

difficulty

in

evaluating these shocks

a

priori;

-

more especially

the

lack

of

consideration

of

these excitations during design,

and

the

absence

of

rigorous

test

specifications.

Figure

3.21.

Example

ofapyroshock

Characteristics

of

shock response spectra

89

Such

shocks have

the

following general characteristics:

- the

levels

of

acceleration

are

very important;

the

shock amplitude

is not

simply

quantity

of

explosive used [HUG 83b]. Reducing

the

load does

not

reduce

the

consequent shock.

The

quantity

of

metal

cut by a jet

cord

is, for

example,

a

more significant factor;

- the

signals assume

an

oscillatory shape;

- in the

near-field, close

to the

source (material within about

15 cm of

point

of

detonation

of the

device,

or

about

7 cm for

less intense pyrotechnic devices),

the

effects

of the

shocks

are

primarily related

to the

propagation

of a

stress wave

in the

material;

- the

shock

is

then propagated

whilst

attenuating

in the

structure.

The

mid-field

(material within about

15 cm and 60 cm for

intense pyrotechnic devices, between

3 cm and 15 cm for

less intense

devices)

from,

which

the

effects

of

this wave

are not

yet

negligible

and

combine with

a

damped oscillatory response

of the

structure

at its

frequencies of

resonance,

is to be

distinguished

from the

far-field,

where only this

last

effect

persists;

- the

shocks have very close components according

to

three axes; their positive

and

negative

response

spectra

are

curves that

are

coarsely symmetrical with

respect

to the

axis

of the frequencies.

They begin

at

zero

frequency

with

a

very small slope

at

the

origin, grow with

the frequency

until

a

maximum located

at

some kHz, even

a

few

tens

of

kHz,

is

reached

and

then tend according

to the

rule towards

the

amplitude

of the

temporal signal.

Due to

their

contents

at

high

frequencies,

such

shocks

can

damage

electric

or

electronic

components;

- the a

priori estimate

of

the

shock levels

is

neither easy

nor

precise.

These

characteristics make them

difficult

to

measure, requiring sensors that

are

able

to

accept

amplitudes

of

100,000

g, frequencies

being able

to

exceed

100

kHz,

with

important transverse components. They

are

also

difficult

to

simulate.

The

dispersions observed

in the

response spectra

of

shocks measured under

comparable

conditions

are

often

important

(3 dB

with more than

8 dB

compared

to

the

average value, according

to the

authors [SMI

84]

[SMI 86]),

The

reasons

for

this

dispersion

are in

general related

to

inadequate instrumentation

and the

conditions

of

measurement

[SMI 86]:

- fixing the

sensors

on the

structure using insulated studs

or

wedge which

act

like

mechanical

filters;

-

zero

shift,

due to the

fact that high accelerations make

the

crystal

of the

accelerometer work

in a

temporarily non-linear

field.

This

shift

can

affect

the

calculation

of the

shock response spectrum (cf. Section 3.10.2.);

-

saturation

of

the

amplifiers;

90

Mechanical shock

-

resonance

of

the

sensors.

With

correct instrumentation,

the

results

of

measurements carried

out

under

the

same

conditions

are

actually very close.

The

spectrum does

not

vary

with

the

tolerances

of

manufacture

and the

assembly tolerances.

3.10.

Care

to be

taken

in the

calculation

of

spectra

3.10.1.

Influence

of

background

noise

of

the

measuring

equipment

The

measuring equipment

is

gauged according

to the

foreseeable amplitude

of

the

shock

to be

measured. When

the

shock characteristics

are

unknown,

the

rule

is to

use a

large effective range

in

order

not to

saturate

the

conditioning module. Even

if

the

signal

to

noise ratio

is

acceptable,

the

incidence

of the

background noise

is not

always

negligible

and can

lead

to

errors

of the

calculated spectra

and the

specifications

which

are

extracted

from it. Its

principal

effect

is to

increase

the

spectra artificially (positive

and

negative), increasing with

the frequency and Q

factor.

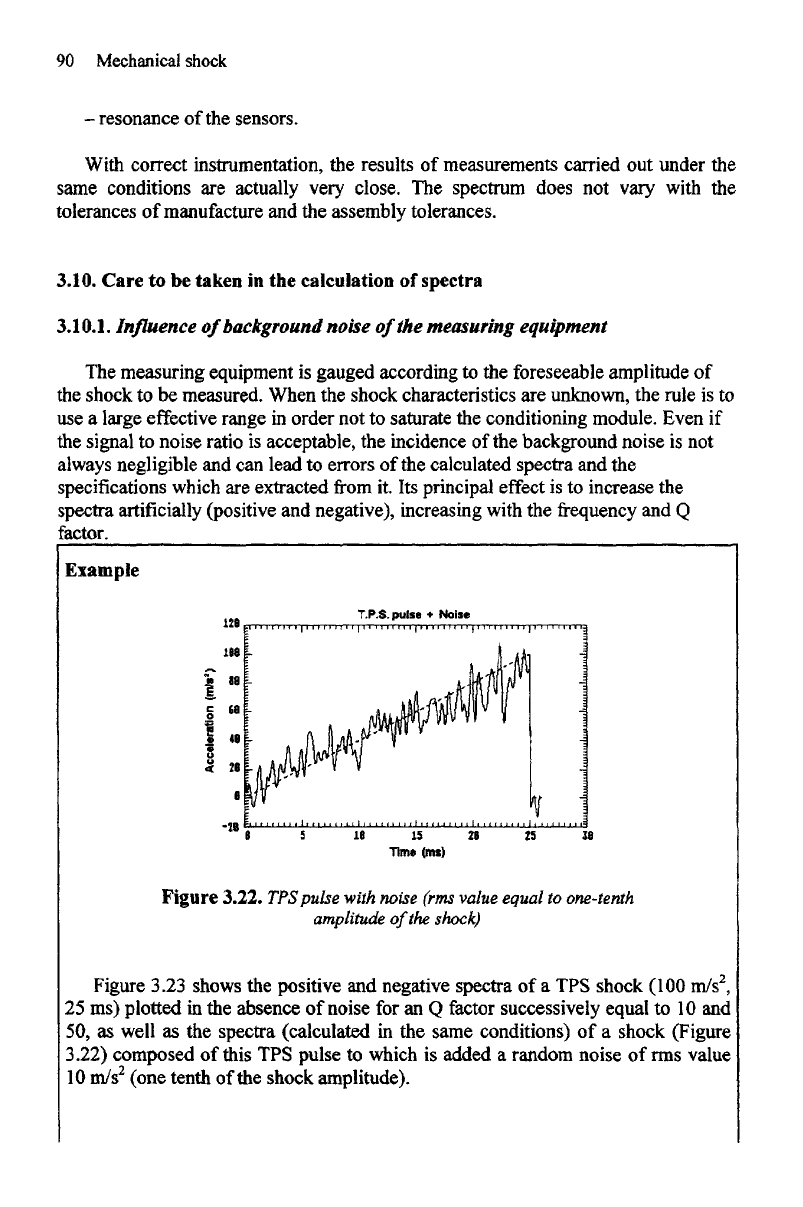
Example

Figure

3.22.

TPSpulse

with noise (rms value equal

to

one-tenth

amplitude

of

the

shock)

Figure

3.23 shows

the

positive

and

negative

spectra

of a TPS

shock (100 m/s

2

,

25 ms)

plotted

in the

absence

of

noise

for an Q

factor

successively equal

to 10 and

50,

as

well

as the

spectra

(calculated

in the

same conditions)

of a

shock (Figure

3.22) composed

of mis TPS

pulse

to

which

is

added

a

random noise

of rms

value

10

m/s

2

(one tenth

of the

shock amplitude).

Characteristics

of

shock response spectra

91

Due

to its

random nature,

it is

practically impossible

to

remove

the

noise

of the

measured

signal

to

extract

the

shock alone

from it.

Techniques, however have been

developed

to try to

correct

the

signal

by

cutting

off the

Fourier transform

of the

noise

from

that

of the

total signal (subtraction

of the

modules, conservation

of the

phase

of the

total

signal) [CAI 94].

Figure

3.23. Positive

and

negative

SRS

of

the

TPS

pulse

and

with noise

92

Mechanical shock

3.10.2.

Influence

of

zero

shift

One

very

often

observes

a

continuous component superimposed

on the

shock

signal

on the

recordings,

the

most

frequent

origin being

the

presence

of a

transverse

high

level component which disturbs

the

operation

of the

sensor.

If

this component

is

not

removed

from the

signal before calculation

of the

spectra,

it can it

also lead

to

considerable errors [BAG

89]

[BEL 88].

When

this continuous component

has

constant amplitude,

the

signal treated

is in

fact

a

rectangle modulated

by the

true signal.

It is not

thus surprising

to find on the

spectrum

of

this composite signal

the

characteristics, more

or

less marked,

of the

spectra

of a

rectangular shock.

The

effect

is

particularly

important

for

oscillatory

type shocks (with zero

or

very small velocity change) such

as, for

example, shocks

of

pyrotechnic origin.

In

this last case,

the

direct component

has as a

consequence

a

modification

of the

spectrum

at low frequencies

which results

in

[LAL 92a]:

- the

disappearance

of the

quasi-symmetry

of the

positive

and

negative spectra

characteristic

of

this type

of

shocks;

-

appearance

of

more

or

less clear lobes

in the

negative spectrum, similar

to

those

of a

pure rectangular shock.

Example

Figure 3.24. 24.

pyrotechnic shock with zero shift

Characteristics

of

shock response

spectra

93

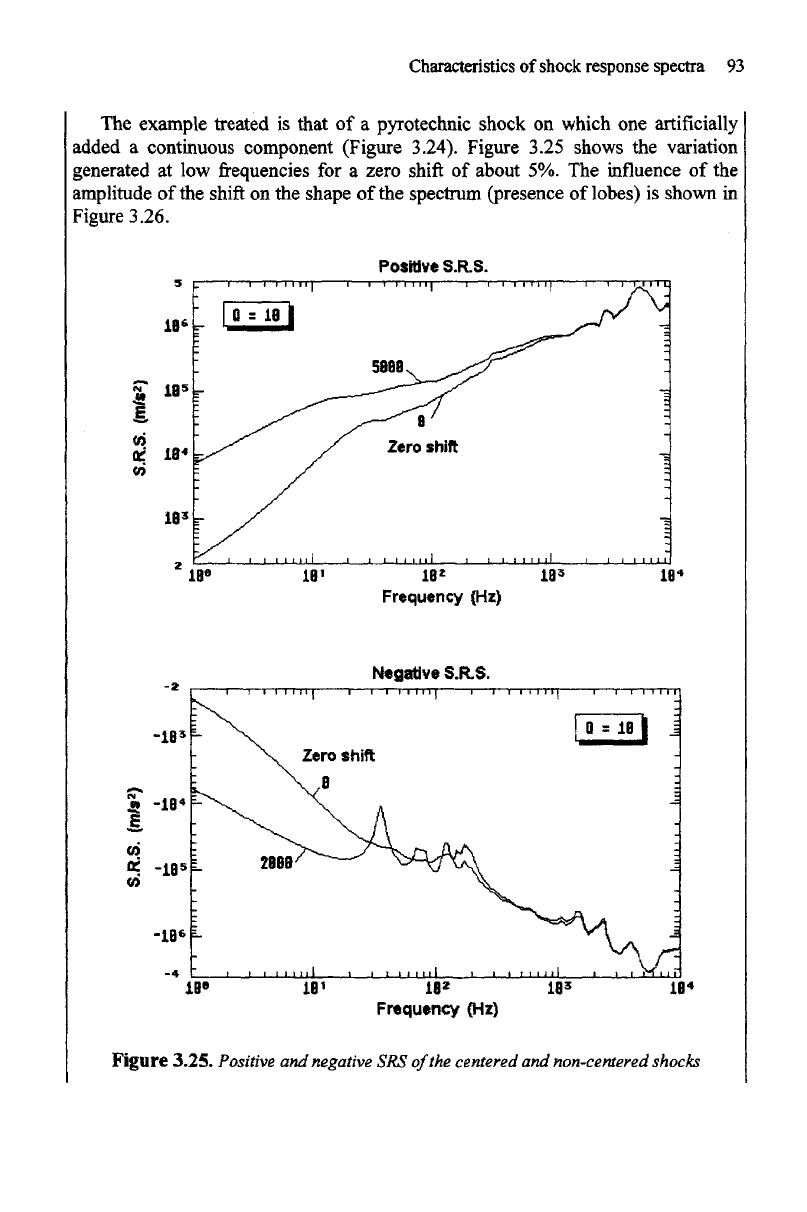
The

example treated

is

that

of a

pyrotechnic shock

on

which

one

artificially

added

a

continuous component (Figure

3.24).

Figure 3.25 shows

the

variation

generated

at low frequencies for a

zero

shift

of

about

5%. The

influence

of the

amplitude

of the

shift

on the

shape

of the

spectrum (presence

of

lobes)

is

shown

in

Figure

3.26.

Figure 3.25.

Positive

and

negative

SRS

of

the

centered

and

non-centered shocks

Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II

Подождите немного. Документ загружается.