Кузюрин Н.Н. Фомин С.А. Сложность комбинаторных алгоритмов. Курс лекций

Подождите немного. Документ загружается.

Сложность комбинаторных алгоритмов. Курс лекций.

Николай Николаевич Кузюрин, Станислав Александрович Фомин

8 января 2007 г.

Оглавление

1 Элементы теории сложности 4

1.1 Несложно о сложности. Примеры алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1.1 Примеры задач на натуральных числах. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1.2 Приближенные алгоритмы. Многопроцессорные расписания . . . . . . . . . . . . . . . . . . . . . 8

1.1.3 Примеры задач на графах. Кратчайшие пути и задача коммивояжера. . . . . . . . . . . . . . . . . 8

1.1.4 Сортировка слиянием . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

1.1.5 Быстрая сортировка. Анализ в среднем и вероятностная версия. . . . . . . . . . . . . . . . . . . . 17

1.2 Формально об алгоритмах . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

1.2.1 Машины с произвольным доступом (RAM) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

1.2.2 Машины Тьюринга и вычислимость . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

1.3 Сложность алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

1.3.1 Сложность в худшем случае (Worst Case Complexity) . . . . . . . . . . . . . . . . . . . . . . . . . 36

1.3.2 Полиномиальные алгоритмы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

1.3.3 Полиномиальность и эффективность . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

1.3.4 Эффективность и классы DTIME, DSPACE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

1.3.5 Полиномиальные сводимости и NP-полнота . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

1.3.6 Сводимость по Куку . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

1.3.7 Недетерминированные алгоритмы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

1.3.8 Сводимость по Карпу . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

1.4 Вероятностные вычисления . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

1.4.1 Классы RP и coRP. Распознавание с односторонней ошибкой. . . . . . . . . . . . . . . . . . . . . 49

1.4.2 Класс BPP. Эффективное распознавание с двухсторонней ошибкой. . . . . . . . . . . . . . . . . . 51

1.4.3 Класс PP. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53

1.4.4 Класс ZPP. Вероятностное распознавание без ошибок. . . . . . . . . . . . . . . . . . . . . . . . . 54

1.5 Вероятностно проверяемые доказательства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

1.5.1 PCP и неаппроксимируемость . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

1.6 Схемы и схемная сложность . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60

1.7 Коммуникационная сложность. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

1.8 Диаграмма классов сложности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66

2 Приближенные алгоритмы с гарантированными оценками точности 67

2.1 Приближенные алгоритмы с фиксированными оценками точности . . . . . . . . . . . . . . . . . . . . . . 67

2.1.1 Жадный алгоритм в задаче о покрытии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

2.1.2 Приближенные алгоритмы для задачи покрытия с минимальной суммой . . . . . . . . . . . . . . 69

2.1.3 Жадный алгоритм для задачи о рюкзаке . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72

2.1.4 Алгоритм Кристофидеса для метрической задачи коммивояжера . . . . . . . . . . . . . . . . . . . 73

2.2 Приближенные алгоритмы с выбираемыми оценками точности . . . . . . . . . . . . . . . . . . . . . . . . 79

2.2.1 Динамическое программирование для задачи о рюкзаке . . . . . . . . . . . . . . . . . . . . . . . . 79

2.2.2 Полностью полиномиальная приближенная схема для задачи о рюкзаке . . . . . . . . . . . . . . 82

3 Вероятностные алгоритмы и вероятностный анализ. 88

3.1 Вероятностный анализ детерминированных алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88

3.1.1 Задача упаковки. Анализ сложности в среднем. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88

3.1.2 Точность жадного алгоритма для почти всех исходных данных . . . . . . . . . . . . . . . . . . . . 92

3.1.3 Полиномиальный в среднем алгоритм для задачи о рюкзаке . . . . . . . . . . . . . . . . . . . . . 94

3.2 Вероятностные алгоритмы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

3.2.1 Алгоритм Фрейвалда . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

3.2.2 Вероятностные методы в перечислительных алгоритмах. Подсчет числа выполняющих наборов

для ДНФ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98

3.2.3 Вероятностный алгоритм Луби нахождения максимального по включению независимого множе-

ства в графе . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100

3.3 Вероятностные методы в распределенных вычислениях . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

3.3.1 Протокол византийского соглашения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

3.4 Вероятностное округление и дерандомизация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105

3.4.1 Вероятностное округление . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105

3.4.2 Приближенный алгоритм для задачи о максимальном сечении . . . . . . . . . . . . . . . . . . . . 107

3.4.3 Дерандомизация и метод условных вероятностей. . . . . . . . . . . . . . . . . . . . . . . . . . . . 110

3.4.4 Дерандомизация вероятностного алгоритма Луби нахождения максимального по включению неза-

висимого множества в графе . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

4 Криптография 115

4.1 Генераторы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

4.1.1 Псевдослучайные генераторы. Генератор Нисана-Вигдерсона . . . . . . . . . . . . . . . . . . . . 115

4.1.2 Полиномиальный алгоритм распознавания простоты числа . . . . . . . . . . . . . . . . . . . . . . 116

4.2 Элементы криптографии с открытым ключом . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120

4.2.1 Односторонние функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120

4.2.2 Дискретный логарифм. Обмен ключами. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120

4.2.3 Система RSA и ее анализ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121

5 Приложения 124

5.1 Глоссарий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124

5.2 Введение в Python . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124

Глава 1

Элементы теории сложности

При написании этого раздела использовались материалы из [Lov, Н.Н96].

1.1 Несложно о сложности. Примеры алгоритмов

Понятие алгоритма в математике используется давно, но различные его формализации были предложены только в

середине 30-х годов прошлого столетия, когда и стала складываться теория алгоритмов.

Классическая теория алгоритмов вообще не интересуется сложностными аспектами (временем решения задач на

реальных вычислителях). В рамках классической теории алгоритмов, ставятся и решаются задачи о разрешимости

различных задач, однако вычислительная сложность полученных решений принципиально не исследуется.

Однако с практической точки зрения, может не быть никакой разницы между неразрешимой задачей и задачей,

решаемой за время Ω(exp(n)), где n — длина входа. Таким образом реализации алгоритмов на реальных вычислитель-

ных машинах обязательно требуют анализа сложности их выполнения. Анализом задач с точки зрения вычислительной

сложности занимается раздел теории алгоритмов — теория сложности вычислений, активно развивающийся с 50х

годов — с момента создания вычислительной техники. Теория сложности вычислений занимает промежуточное поло-

жение между строгой математикой и реальным программированием. Для математика это в первую очередь матема-

тическая теория, строящаяся на основе фундаментальных понятий полиномиальной вычислимости и полиномиальной

сводимости. Для программиста-практика — это набор общих методов, парадигм и конструкций, позволяющий в ряде

случаев существенно минимизировать прямолинейный перебор вариантов, а в ряде случаев — показать, что эта за-

дача в рассматриваемой постановке скорее всего неразрешима (и, следовательно, следует искать более реалистичные

постановки).

Для подавляющего большинства комбинаторных алгоритмических задач существует простой прямолинейный ал-

горитм, основанный на переборе всех или почти всех вариантов. В ряде случаев (скажем, при небольших размерах

входных данных) такой подход вполне удовлетворителен.

Теория сложности вычислений начинается в тот момент, когда прямолинейные (в нашем случае — переборные)

алгоритмы становятся неприемлемыми или, по меньшей мере, экономически невыгодными, ввиду роста сложности ре-

шаемых оптимизационных задач.

Заметим, что выбор конкретной программной реализации выходит за рамки теории сложности. Поэтому алгоритмы

обычно описываются на наиболее примитивном, алголоподобном языке. В нашем курсе, мы часть алгоритмов будет

приводить в виде реализованных программ на языке Python ( ), что позволит избежать неяс-

ностей, свойственных псевдоописаниям (т.к. псевдоописание не «верифицировано» реальным выполнением), и достичь

понимаемости алгоритма с другой стороны, т.к. этот язык был признан идеальным выбором для преподавания инфор-

матики и курсов по алгоритмам.

1.1.1 Примеры задач на натуральных числах.

Мы начнем рассмотрение парадигмы сложности с простой задачи о натуральных числах.

Итак, даны три натуральных числа x, n, и m. Требуется вычислить y = x

mod m. (Деление по модулю здесь

добавлено, чтобы не касаться проблем связанных с длиной операндов).

Легко придумать следующий прямолинейный алгоритм (См. алгоритм 1), который в цикле от 1 до n выполняет

следующее действие: y ← y · x mod m.

Очевидный анализ показывает сложность этого алгоритма — O(n). Пока, на неформальном уровне, под сложно-

стью мы будем понимать число элементарных операций.

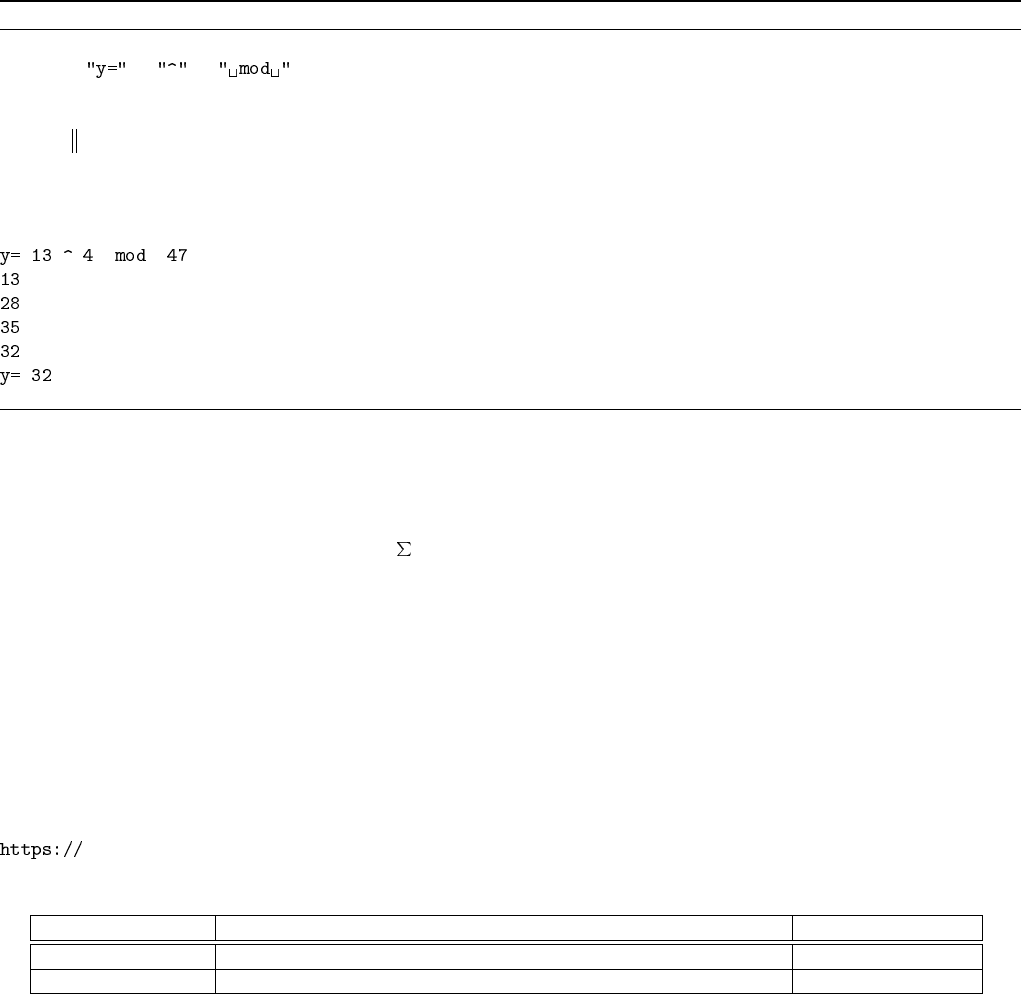
Алгоритм 1 Тривиальное вычисление y = x

mod m

def mod_exp (x, n, m):

print , x, , n, , m

y ← 1

for i ∈ range (1, n + 1):

Напомним, что x

mod m ≡ (x mod m)

mod m

y ← y ∗ x % m

print y

return y

Можно существенно улучшить алгоритм 1, использовав соображения, основанные на двоичном разложении по-

казателя степени (См. алгоритм 2). Действительно, рассмотрев двоичное разложение n =

i=0

, где a

∈ {0, 1},

заметим, что

= x

i=0

{i:a

>0}

Т.е. достаточно провести l ≤ (log

n + 1) итераций по двоичному разложению n, чтобы на каждой i-й итерации, в

зависимости от i-го бита в разложении, проводить домножение результата на сомножитель x

, который легко получить

из сомножителя предыдущей итерации (ключевое соотношение):

← (x

(i−1)

)

Анализ же этого алгоритма (алгоритм 2) показывает что его сложность — O(log n). Как видно, разница в сложности

двух алгоритмов экспоненциальна!

Заметим, что процедура расчета модульной экспоненты весьма распространена в различных сетевых протоко-

лах, например при установке защищенного интернет-соединения (всякий раз, когда в браузере адрес начинается с

, при установке соединения работают алгоритмы криптографии и вычисляется модульная экспонента). Если

взять длину ключа 128-бит (длина показателя экспоненты близка к длине ключа), то получается простое сравнение,

количества умножений в обоих алгоритмах:

Длина ключа (бит) Умножений в алг. 1 Умножений в алг. 2

56 2

= 72057594037927936 ≈ 7.2 · 10

≈ 56

128 2

128

= 340282366920938463463374607431768211456 ≈ 3.4 · 10

≈ 128

Комментарии излишни.

Теперь рассмотрим примитивный алгоритм точного вычисления факториала (по модулю m) (см. алгоритм 3 «Фак-

ториал»). Нетрудно видеть, что его сложность — O(n). Можно ли ее существенно улучшить, как в случае с возведением

степень? Оказывается, на сегодняшний день это является известной открытой проблемой (См. следствия из Problem

4 в [Sma00]).

Рассмотрим еще одну очень важную задачу, связанную с возведением в степень по модулю.

Задача 1 Дискретный логарифм.

Пусть p — нечетное простое число. Известны натуральные a и b и выполняется соотношение

≡ b mo d p

Найти x.

По сути эта обратная задача к задаче возведения в степень по модулю. Можем ли мы как и в предыдущем примере

ожидать легкого решения? Оказывается, нет, вычисление дискретного алгоритма является очень сложной задачей и

самые быстрые из известных алгоритмов требуют сверхполиномиального (по длине двоичной записи p) времени. На

этом важном свойстве (свойстве односторонней вычислимости модульной экспоненты) основано множество алго-

ритмов современной криптографии.

Алгоритм 2 Разумное вычисление y = x

mod m

def mod_exp (x, n, m):

print , x, , n, , m

y ← 1

X ← x

N ← n

while (N > 0):

if ((N % 2) = 0) :

X ← X ∗X % m

N ← N/2

else:

y ← y ∗ X % m

N ← N − 1

print N, X, y

return y

Алгоритм 3 Вычисление факториала y = n! mod m

def factorial (n, m):

print , n, , m

y ← 1

for i ∈ range (1, n + 1):

y ← y ∗ i % m

print y

return y

Еще одним примером взаимно обратных преобразований подобного рода являются операции произведения нату-

ральных чисел и разложение на множители. Пусть p и q два простых числа. Тогда не составляет особого труда вычис-

лить их произведение n = pq. Однако, если мы знаем лишь n и требуется найти p и q, то это также труднорешаемая

задача для которой неизвестны эффективные алгоритмы решения. На трудности задачи факторизации (разложения на

множители) основана одна из самых известных криптосистем RSA.

Рассмотрим одну из классических задач — нахождение наибольшего общего делителя (НОД

) двух целых чисел,

и алгоритм Евклида (алгоритм 4 «НОД») для решения этой задачи и проанализируем его (для определенности ниже

будем считать, что a ≤ b.). Базовое соотношение, лежащее в основе алгоритма Евклида таково: gcd(a, b) = gcd(a, r),

b = at + r, 0 ≤ r < a.

Алгоритм 4 Алгоритм Евклида

def gcd (a, b):

print a, b

if a = 0 :

return b

return gcd (b % a, a)

Лемма 1 Время работы алгоритма Евклида (алгоритм 4 «НОД») составляет O(log a + log b) арифметиче-

ских операций над натуральными числами.

Доказательство Имеем: b ≥ a + (b mod a) ≥ 2(b mod a) ≡ 2r. Отсюда получаем, что r ≤

. Таким образом,

ar ≤ ab/2, т.е. произведение ab уменьшается на каждой итерации вдвое, и после dlog(ab)e итераций станет меньше 1,

т.е. равно нулю. А это означает, что a = 0 (т.е. НОД уже найден). 2

Отметим, что длина записи исходных данных в этой задаче есть O(log a + log b) и по порядку совпадает с числом

операций алгоритма Евклида (алгоритм является эффективным).

Алгоритм 5 Неэффективный алгоритм для нахождения НОД

def gcd (a, b):

print a, b

if a = 0 :

return b

return gcd (max (a, b) − min (a, b), min (a, b))

Отметим, что алгоритм 5 «Неэффективный НОД» (модификация алгоритма 4 «НОД», где деление с остатком за-

менено на вычитание меньшего числа из большего), не является столь эффективным. Если b много больше a, число

операций вычитания пропорционально b/a (а не сумме их логарифмов).

Таким образом, мы увидели, что несмотря на внешнюю похожесть, сложность похожих задач может существенно

отличаться. Для обнаружения и понимания такой разницы и нужен анализ сложности, являющийся предметом нашего

курса.

GCD — Greatest Common Divisor, в англоязычной литературе

1.1.2 Приближенные алгоритмы. Многопроцессорные расписания

Не все алгоритмы находят точное решение. Некоторые довольствуются нахождением приближенного (в некотором

смысле) решения. Такие алгоритмы называются приближенными. Для них актуальной задачей является анализ точно-

сти получаемого решения.

Не давая пока формальных определений рассмотрим для иллюстрации одну из простейших задач составления рас-

писаний.

Задача 2 СОСТАВЛЕНИЕ РАСПИСАНИЙ.

Имеется m одинаковых машин и n независимых работ с заданными длительностями исполнения t

, . . . , t

Требуется распределить эти работы по машинам так, чтобы минимизировать максимальную загрузку (за-

грузка машины равна сумме длительностей работ, приписанных данной машине).

Несмотря на простоту постановки эта задача трудна с вычислительной точки зрения (NP-трудна). Даже для случая

m = 2 она остается NP-трудной поскольку к ней сводится так называемая задача о камнях: для заданного множества

из n камней с весами t

, . . . , t

выяснить, можно ли разбить это множество на два так, чтобы суммы весов в них были

равны. Нетрудно проверить, что это условие можно записать в виде булева уравнения:

i=1

= A/2,

где A =

i=1

, x

∈ {0, 1}.

Традиционный подход к задачам такого рода состоит в использовании простых эвристик, одну из которых мы сейчас

проанализируем:

Эвристика: Берется произвольная работа и помещается на машину, имеющую наименьшую загрузку.

Эта эвристика обладает следующим, очевидным свойством:

Лемма 2 В любой момент работы этой эвристики, разница в загрузке между наиболее и наименее загру-

женными машинами не превосходит t

max

= max

Теперь мы можем доказать утвержение о качестве работы нашей эвристики:

Лемма 3 Построенное расписание отличается от оптимального (по критерию минимизации максимальной

загрузки) не более, чем в два раза.

Доказательство Пусть T

∗

— длина оптимального расписания (сумма длин работ на наиболее загруженной машине),

— длина расписания, которое построено нашей эвристикой, T

min

— сумма длин работ на наименее загруженной

машине (в расписании, построенном нашей эвристикой). Имеют место очевидные неравенства:

∗

≥ T

min

∗

≥ t

max

А теперь мы легко можем оценить качество получаемого расписания:

∗

≤

min

+ t

max

∗

≤

∗

+ t

max

∗

≤ 1 +

max

∗

≤ 1 + 1 = 2.

Следует подчеркнуть, что эвристики очень часто используются для решения задач на практике. В рассмотренном

примере алгоритм (эвристика) обладал одним дополнительным свойством: он применим и в случае когда работы посту-

пают одна за другой, поскольку решение о назначении машины для данной работы принимается только на основании

информации о состоянии машин (это так называемые online алгоритмы).

1.1.3 Примеры задач на графах. Кратчайшие пути и задача коммивояжера.

Рассмотрим несколько классических задач на графах.

Задача 3 Коммивояжер

Заданы n городов v

, v

, . . . , v

и попарные расстояния d

≡ d(v

, v

) между ними, являющиеся положи-

тельными целыми числами.

В англоязычной литературе — Traveling Salesman Problem, сокращенно TSP.

n n!

5 120

8 40320

10 3, 6 · 10

13 6, 2 · 10

15 1, 3 · 10

30 2, 7 · 10

Таблица 1.1: Значения функции n!

Чему равна наименьшая возможная длина кольцевого маршрута, проходящего по одному разу через все

города? Иными словами, требуется найти минимально возможное значение суммы

n−1

i=1

π (i) ,π(i+1)

+ d

π (n),π(1)

, (1.1)

где минимум берется по всем перестановкам π(1), . . . , π(n) чисел 1, . . . , n.

Переборный алгоритм для задачи о коммивояжере просто перебирает все возможные перестановки городов (см.

алгоритм 6 «TSP-перебор»).

При анализе сложности алгоритма 6 «TSP-перебор» видно, что вычисление индивидуальной суммы (1.1) не пред-

ставляет особых трудностей и требует Cn операций, где C-некоторая константа. Проблема состоит в том, что этот

процесс придется повторить слишком много, (n − 1)! раз, что дает общую сложность алгоритма Ω(n!). Некоторые

значения факториала приведены в таблице 1.1.

Видно, что при n = 5 расчет всех вариантов согласно переборному алгоритму может быть произведен вручную.

При n = 8 для его проведения в разумный отрезок времени нужно привлечь программируемый калькулятор, а при

n = 10 — уже более быстродействующую вычислительную технику. Когда число городов доходит до 13, потребуется

суперкомпьютер, а случай n = 15 выходит за пределы возможностей любой современной вычислительной техники.

Число возможных вариантов при n = 30 превышает количество атомов на Земле

Теперь рассмотрим задачу 4 «Shortest Path», на первый взгляд похожую на Задачу 3 «TSP»:

Задача 4 «Кратчайший путь в графе»

Заданы n вершин графа (узлов сети) v

, v

, . . . , v

и положительные целые длины дуг d

≡ d(v

, v

) между

ними.

Чему равна наименьшая возможная длина пути, ведущего из v

в v

, для всех k ∈ (2 . . . n)? Иными словами,

чему равно минимально возможное значение суммы

`−1

i=1



σ (i)

, v

σ (i+1)



, (1.2)

где минимум берется по всем числовым последовательностям

σ(1), . . . , σ(`)

(на этот раз не обязательно длины n), в которых σ(1) = 1 и σ(`) = n.

Разумеется, и эту задачу можно решать переборным алгоритмом, аналогичным алгоритму 6 «TSP-перебор», но

интересно, можно ли разработать точный эффективный алгоритм, исключающий (или, по меньшей мере, минимизиру-

ющий) непосредственный перебор вариантов.

Оказывается, в данном случае можно. Здесь важным фактом является то, что если у нас есть кратчайший путь от v

до w, проходящий через вершину y, назовем его (v → w)

∗

, то его первая часть от v до y, (v → y)

∗

, тоже будет кратчай-

шим путем. Действительно, если бы это было не так, т.е. существовал бы путь (v → y)

длины меньшей, чем (v → y)

∗

то можно было бы улучшить оптимальный путь (v → w)

∗

, заменив в нем (v → y)

∗

на (v → y)

. Задачи, с подобными

Конечно, разработаны различные методы сокращения перебора, кроме того, переборные задачи допускают эффективное распараллеливание на

многопроцессорную технику или вычисление сетью обычных компьютеров. В частности, в 2001 году, для задачи 3 «TSP» на 15112 городах Германии,

было найдено оптимальное решение на 110 процессорном кластере. Если измерять вычислительное время относительно одного процессора «Compaq

EV6 Alpha 500 МГц», то было потрачено 22.6 лет. См. отчет . Но это не отменяет высказанных соображений

о непрактичности использования экспоненциальных алгоритмов перебора, кроме случаев входных данных ограниченного размера

В англоязычной литературе — Shortest Path Problem.

Алгоритм 6 Переборный алгоритм для задачи 3 «TSP»

Находит и возвращает гамильтонов цикл минимального веса в графе G. Использует перебор по всем вершинам кроме

первой.

def tsp_permutations (G):

← 1·10

300

# устанавливаем минимальную длину в бесконечность

← [ ]

← G.nodes ()[0] # Фиксируем начальный узел (сокращаем перебор).

for ∈ xpermutations (G.nodes ()[1 : ]): # перебор всех узлов кроме первого.

.insert (0, ) # добавляем в начало пути стартовый узел

← 0 # обнуляем длину текущего пути

← 1 # Сначала считаем, что путь проходим

for i ∈ xrange (len ( )):

← [i] # выбираем ребро (v1,v2), для текущей вершины

if i < len ( ) − 1:

← [i + 1]

else:

← [0] # Если нода-последняя, то замыкаем путь.

if G.has_edge ( , ):

← + G.get_edge ( , )

else:

← 0 # нет ребра (v1,v2) - путь непроходим.

break

if ( ):

print ,

if > :

←

print , ,

return

Berlin

$50

Moscow

$60

Kiev

$80

$30

$50

$10

Minsk

$15

$20

$15