Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

Раздел 6

222

()

1к 1ндд11 1

кндд

И ,

rr rrr

NN NN

iia tb

ννν

νν ν

=⎡ + γ ⎤

⎣⎦

=⎡ + γ ⎤

⎣

⎦

⎡+γ ⎤

⎣

⎦



(6.18)

в которые входят неизвестные начальные и конечные ординаты

в количестве 2N. Конечная ордината предыдущего участка явля-

ется начальной для последующего. Это позволяет записать еще

N выражений:

1к 2нк1,нк1н

,, ,,

rr N

ii ii i i

νν νν+ ν ν

=……=

(6.19)

Решением системы алгебраических уравнений находятся

ординаты на границах участков и подставляются в (6.17), после

чего по полученным выражениям определяется эффективное

значение несинусоидальной компоненты тока двигателя.

При кусочно-линейном графике помехи в пределах участ-

ка помеха имеет вид at + c, где а и с – постоянные коэффициен-

ты. В этом случае

() ( )

[

]

{}

{

}

И exp ,tTatTc taTc=−+γ+−

а при ступенчатом графике с величиной ступени с

()

{

}

(

)

И exp 1 .tcT t

γ−

Например, график на рис. 5.1,б имеет один прямоуголь-

ный импульс величиной с = –В. Расположим оси координат в

начале импульса. Это дает возможность использовать формулы

(2.57) и (2.58), заменив в них

на –В,

на 0, t

на θ и t

на t

Начальная и конечная ординаты реакции ВФ составят

Методы расчета показателей ЭМС по несинусоидальности напряжения

223

нд 2 кд

iaB biaB

νν νν

−

=− =−

−−

b−

(6.20)

где

{

}

(

)

{

}

{

}

1 д 2 дд

exp , exp , exp .

bbtb=−γθ =−γ−θ =−γ

Реакция ВФ определяется выражениями:

()

{

}

{

}

(

)

()

{}

ндд д

кд

exp 1 exp при 0,

exp при .

itaB t t

it t

νν

⎧

−

γ− − −γ ≤≤θ

⎪

⎨

−

γ−θ θ≤≤

⎪

⎩

(6.21)

Квадрат эффективного тока

()

(

)

(

)

22 12дд

ff f

bbTaB

iitdt

tt b

νν

⎡

−−

==θ−

⎤

⎢

⎥

−

⎣

⎦

∫

(6.22)

Следует отметить, что эту величину можно определить и

по плотности распределения реакции, которая согласно (2.65)

имеет вид

()

дд

aBT

ti aB i

νν

−

(6.23)

Интегрирование по формуле

()

iifid

νν

∫

дает тот же результат, что и (6.22).

Рассмотренные способы требуют построения графика ре-

акции. Эффективный ток можно определить и без этой процеду-

ры, если предварительно вычислить корреляционную функцию

Раздел 6

224

помехи и по формуле (2.61) найти дисперсию Di

реакции. Тогда

222

эдс

,iauDi

νν ν

(6.24)

где первое слагаемое представляет собой квадрат среднего зна-

чения реакции. Как отмечено в п. 6.2, среднее значение обычно

равно нулю.

Квадрат эффективного значения помехи равен

tθ

по-

этому оценивание ЭМС по этой величине, а не по (6.22), приве-

ло бы к завышению требований в

()()

эд 12д

11 1

ia b bT

νν ν

−

−− θ

раз.

Перейдем к непериодическим помехам. Эффективный ток

может быть определен методом гармонического анализа, но по

квазиграмоникам (п. 5.1). Однако в большинстве случаев целе-

сообразно строить график реализации ВФ интервальным мето-

дом. В соответствии с формулой (2.56) для момента времени r∆

ордината реакции

(

)

нд

1 при 1, , 1,

rr r

iibau b r N

νν∆ νν ∆

=+ − = −…

(6.25)

где

{

}

exp .b

∆

=−γ∆

В начальный момент времени t = 0 ток ра-

вен нулю, поэтому при r = 1 первое слагаемое равно нулю.

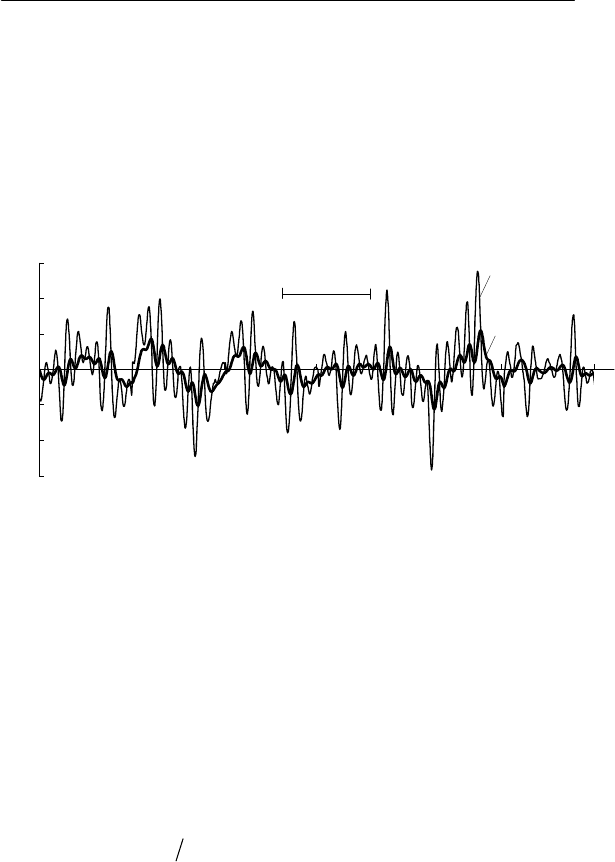
На рис. 6.7 кривой 1 представлен исходный график поме-

хи, а кривой 2 – график реакции, рассчитанный согласно (6.25).

Из него исключается участок переходного процесса от 0 до 3Т

дν

= 0,0037 с, а по оставшейся части вычисляется эффективное

значение i

νэ

несинусоидальной компоненты тока.

С учетом (5.13), (5.14) и (1.37) определим дополнительное

повышение температуры

ϑν

∆ϑ =

(6.26)

Методы расчета показателей ЭМС по несинусоидальности напряжения

225

кратность снижения срока службы

{

}

{

}

exp exp ,

bbc

ννν

γ= ∆ϑ =

(6.27)

а также уменьшение срока службы в %

(

)

1 100.

νν

∆=γ−

(6.28)

-15

-10

-5

% u

, i

0,02 с

Рис. 6.7. График несинусоидальной компоненты тока дви-

гателя при искажениях кривой напряжения в сети 6 кВ

Увеличение сопротивления двигателя с ростом частоты

приводит к сильному сглаживанию кривой 2 по сравнению с

кривой 1. По этой причине ЭМС двигателя нельзя оценивать по

коэффициентам искажений, которые дают существенное завы-

шение требований.

В рассматриваемом примере эффективный ток оказался

равным 1,71 %. Результаты расчетов по формулам (6.26)-(6.28)

приведены в табл. 6.1, в которой для сравнения в скобках указа-

ны значения показателей, рассчитанные по эффективному зна-

чению коэффициента искажений, равному 4,1 %. Температура

завышается в

()

4,1 1,71 5,75=

раза, а уменьшение срока служ-

бы – от 6,33 до 9,59 раза.

Дополнительные потери активной мощности

эPi

Pci

∆ν

∆=

(6.29)

Раздел 6

226

рассчитываются по эффективному току и коэффициентам (5.16)

и (5.17). Например, для СД с успокоительной обмоткой

52 4

нэ н

8,86 10 2,59 10 ,PPi

−−

νν

∆= ⋅ = ⋅ P

а без нее

кВт.

52 4

нэ н

3,46 10 1,01 10 ,PPi

−−

νν

∆= ⋅ = ⋅

Расчет же по эффективному значению коэффициентов ис-

кажения завышает потери в 5,75 раза.

Таблица 6.1 – Повышение температуры и уменьшение

срока службы двигателей от несинусоидальности напряжения в

сети 6 кВ

Двигатель

Класс

изоляции

∆ϑ

νс

°С

zν

∆z

1,31

(7,55)

АД

1,64

(9,44)

1,12

(1,92)

(92)

2,29

(13,1)

СД с успокои-

тельной обмоткой

2,86

(16,42)

1,22

(3,11)

(211)

0,94

(3,24)

СД без успокои-

тельной обмотки

1,14

(6,54)

1,09

(1,57)

(57)

Если случайная помеха задана корреляционной функцией,

то квадрат эффективного значения реакции определяется по

формуле (6.24). Первое слагаемое в ней известно, а дисперсия

реакции вычисляется согласно (2.61) или табл. 2.2. Например,

для КФ (6.8) получим

Методы расчета показателей ЭМС по несинусоидальности напряжения

227

()

д 0 д

Di a D

νν ν

νν

+α

+α +ω

∑

(6.30)

Подстановка численных значений дает а

дν

νс

= −0,18 %,

= 3,1 (%)

и i

νэ

= 1,76 %. Относительная погрешность опре-

деления эффективного тока по графику и его вероятностным

характеристикам (1,71 против 1,76) составила 2,92 %.

6.5. Оценивание влияния несинусоидальности напряжения

на конденсаторные установки

Расчеты показателей ЭМС для КУ аналогичны таковым

для электродвигателей (п. 6.4) с тем отличием, что структуры

ВФ в моделях ЭМС различны. Оценивание ЭМС осуществляет-

ся по эффективным значениям i

Cνэ

несинусоидальной компонен-

ты тока КУ и у

∆Рэ

реакции ВФ по потерям мощности (рис. 5.10 и

5.11).

Рассмотрим вначале периодическую помеху с периодом t

При использовании ряда (6.13) с учетом (5.24) найдем среднее

значение несинусоидальной компоненты

сCC

iku

(6.31)

и амплитуду п-ой гармоники

()

22 22

11 10

In C Un

BkB

+ω

+ω +ω

(6.32)

Фазы гармоник на эффективное значение не влияют:

(

)

()

min min

2222

222

эс с

22 2 22 2

11 10

Un f

CC Un

KnT

ii Bu

nT nT

∞∞

νν ν

+ω

=+ =+

−ω +ω

∑∑

(6.33)

Раздел 6

228

Вследствие малости коэффициента k

, среднее значение

тока практически равно нулю, поэтому погрешность в опреде-

лении среднего значения помехи (п. 6.2) не приводит к большой

погрешности оценивания тока.

Второй способ заключается в построении графика тока

КУ в стационарном режиме. Для использования метода парци-

альных реакций (п. 2.2) по формулам (2.3), (2.4) и (5.23) найдем

сопрягающие частоты

1,2 1,2CCC

γ=−=α λ∓

(6.34)

и коэффициенты передачи инерционных звеньев

()() ()

11 1 2 11 1 1 2

CC C

Tp Tp

ak k

Tpp p p p Tp p p

−− −

Подставив сюда выражения (5.22) для полюсов и учиты-

вая, что

22 2

Tα+λ=

получим

()

akjk

где

(

)

711

kTT

−α λ (6.35)

Таким же образом найдем

()

akjk

=−

Методы расчета показателей ЭМС по несинусоидальности напряжения

229

Парциальные реакции определяются по аналогичным

(6.17)-(6.19) выражениям, в которых величина γ

()it



заменяется на

С1,2

, а коэффициент передачи а

дν

на а

С1,2

. Искомая реакция i

Cν

(t)

равна сумме парциальных реакций.

Для помехи, представленной на рис. 5.1,б, вместо выра-

жений (6.20) получим граничные ординаты

1,2 1,2

н1,2 1,2 1,2 к1,2 1,2

1,2

Cf C

fC fC

iaB biaB

θθ

νθν

−

−=−

−−



где

{

}

(

)

{

}

{}

1,2 1,2 1,2 1,2

1,2 1,2

exp , exp ,

exp .

Cf Cf

fC C f

θθ

=−γθ =−γ −θ

=−γ

По аналогии с (6.21) определим несинусоидальную ком-

поненту тока. Учитывая, что

CC C

aa k

при 0 ≤ t ≤ θ получим

(

)

(

)

{

}

()

{}

н11 1

н22 2

exp

exp ,

CCC

it i aB t

iaB tkB

νν

=− −γ+

+− −γ−



а в пределах от θ до t

() ( )

{

}

()

{

}

к11 к22

exp exp .

CC C

it i t i t

νν ν

−γ −θ + −γ −θ



Если длительность провала меньше времени затухания

переходной функции, то реакция в момент скачка равна произ-

ведению величины скачка на переходную функцию с учетом

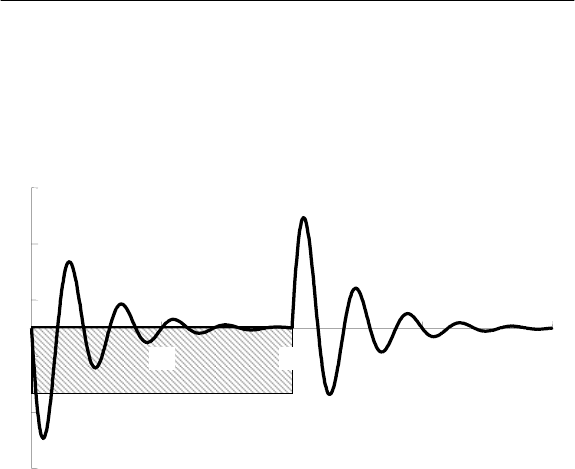
направления скачка. На рис. 6.8 показан фрагмент графика тока

Раздел 6

230

конденсатора при воздействии на него прямоугольного провала

величиной В = 10 % и длительностью 0,4 мс (затушеванная об-

ласть). Время на графике отсчитывается от начала провала. Пе-

реходная функция затухает за такое же время (рис. 5.9). В этом

случае реакция на скачки равна

()

ht∓

t, мс

% i

Cν

-2500

-1500

-500

500

1500

2500

0,2 0,4 0,6 0,8

= –10 %

Рис. 6.8. Несинусоидальная компонента тока силового

конденсатора 26 квар, 380 В при прямоугольном провале в си-

нусоиде напряжения

Как и в (6.22), квадрат эффективного тока определяется

делением на длительность цикла интеграла от квадрата процесса

Cν

(t). В соответствии с динамической моделью ЭМС (рис. 5.10)

средняя температура дополнительного перегрева и кратность

снижения срока службы КУ вычисляются по формулам:

{

}

сэ

,exp

CiC z

ci b

ννν ν ν

∆ϑ = γ = ∆ϑ

(6.36)

Структура формул (5.23) и (5.35) качественно одинакова,

поэтому определение эффективного значения у

∆Рэ

производится

по аналогичным формулам. Для этого в (6.35) постоянная вре-

мени Т

заменяется на Т

, а i

Cν

(t) на у

∆Р

(t). С учетом (5.42) полу-

чим потери мощности в КУ

Методы расчета показателей ЭМС по несинусоидальности напряжения

231

Pc y

ν∆ ∆

∆

(6.37)

Перейдем к непериодической помехе, заданной реализа-

цией. По аналогии с (6.25) запишем выражения для парциаль-

ных реакций:

(

)

1,2 н 1,2 1,2 1,2 1,2

1 при 1, , 1,

Cr C r C r

iibaub r N

νν∆ ν∆

=+− =



…

− (6.38)

где

{

}

1,2 1,2

exp .

∆

=−γ∆ Эти величины являются комплексными,

но их сумма дает действительные ординаты реакции

(6.39)

Cr Cr Cr

ii i

νν ν



так как мнимые величины уничтожаются.

Расчет начинается с нулевых начальных условий. Для по-

лучения стационарного состояния из полученного графика ре-

акции исключается начальная его часть от t = 0 до трех постоян-

ных времени затухания переходного процесса. Эта постоянная

определяется по формуле

11 10

21.

TTT

=α

(6.40)

Для обеспечения достоверности шаг ∆ дискретизации по-

мехи должен быть достаточно малым. В случае линейной ин-

терполяции наибольшая относительная погрешность δ воспро-

изведения синусоиды с угловой частотой ω в процентах от ее

амплитуды определяется выражением [10]

(

)

(

)

100 1 cos 100 1 cos 2 ,N

⎡

⎤⎡

δ= − π = − ω∆

⎤

⎣

⎦⎣ ⎦

(6.41)

где N – отношение периода синусоиды к шагу дискретизации,

причем предполагается, что N < π или ω∆ < 2.

Отсюда по заданной допустимой погрешности δ

доп

полу-

чим выражения для минимального количества интервалов