Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

Раздел 5

192

ва трансформатора от несинусоидальности напряжения. Здесь

также имеется полная аналогия с моделью ЭМС для КУ, пред-

ставленной на рис. 5.10: в обозначениях процессов достаточно

заменить индекс «С» на «т». Поэтому остается найти лишь АЧФ

взвешивающего фильтра и коэффициент передачи с

тϑi

звена 4

после звена 6.

012

0,5

02040608010

тν∆Р

1 и 2

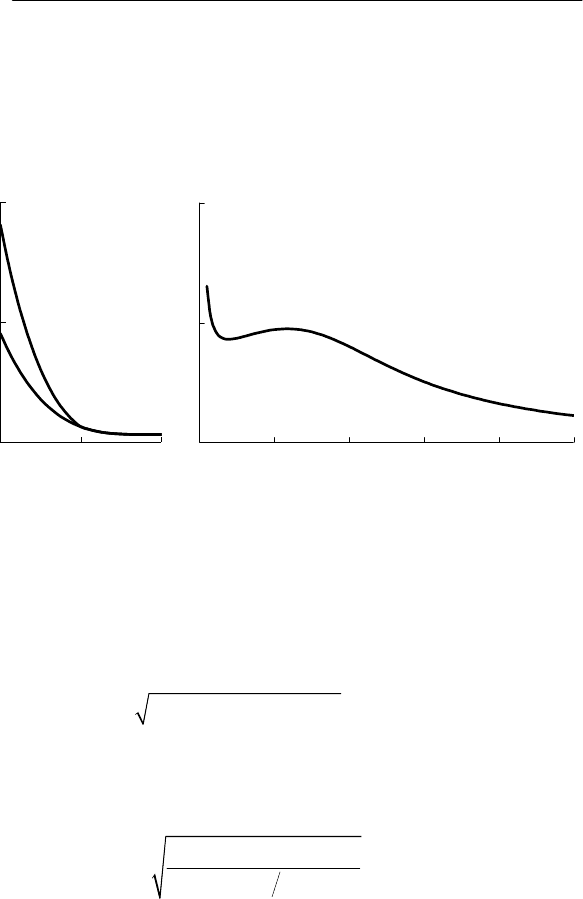
Рис. 5.13. АЧФ взвешивающих фильтров модели ЭМС с ФНЧ по

потерям активной мощности от несинусоидальности напряжения

для трансформаторов: 1 – цеховых, 2 – специальных

В пределах ν от 2 до п

, как и в (5.51), замена в формуле

(5.43) номера гармоники на ν дает АЧФ части ВФ:

()

1,5 0,5 2

т 123 п

при 2

kd d d n

−−

νϑ

ν= ν + ν + ν ≤ν≤



(5.59)

где k

– коэффициент передачи ВФ.

С учетом АЧФ (5.48) для ВФ в целом получим

()

1,5 0,5 2

123

т п

при

ddd

−−

νϑ

ν+ν+ν

ν= ν≥

+ν

(5.60)

Поскольку АЧФ модели для потерь мощности известна,

при определении АЧФ модели для температуры на участке зна-

Математические модели для оценивания параметров несинусоидальных режимов

193

чений ν от 0 до 2 будем исходить из отношения

() () ()

тт

kA A

ν∆ νϑ

ν= ν ν



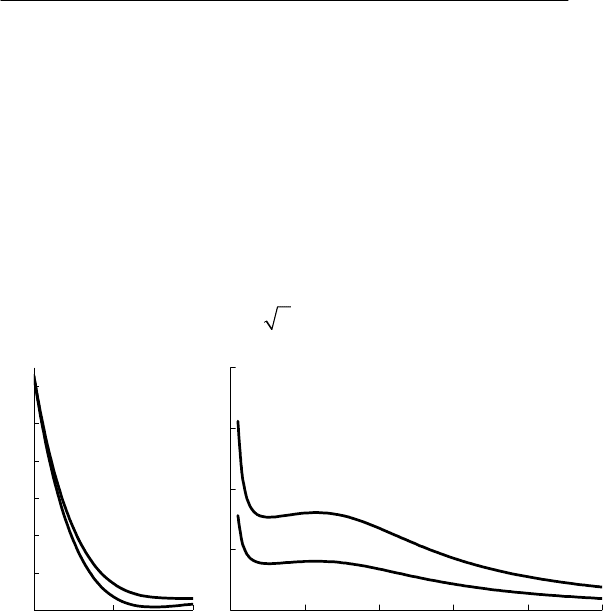
На рис. 5.14 показаны кривые отношений АЧФ, рассчи-

танных по формулам (5.51) и (5.59). Пропорциональность между

АЧФ начинает проявляться при п > 10, а нарушение пропорцио-

нальности особенно заметно при малых частотах. Этого и сле-

довало ожидать, так как в формуле (5.59) есть третье слагаемое,

которое с уменьшением частоты увеличивает АЧФ в модели для

температуры в

большей мере, чем АЧФ (5.51).

0,01

0,02

0,03

0,04

0,05

0 5 10 15 20

Рис. 5.14. Отношение АЧФ взвешивающих фильтров по потерям

активной мощности и температуре для цеховых (1) и специаль-

ных (2) трансформаторов

Кривые на рис. 5.14 были аппроксимированы следующи-

ми выражениями: для цеховых трансформаторов

()

{}

(

)

0,0106 1,9434 exp 0,278ρν = − − ν (5.61)

Раздел 5

194

с погрешностью менее 0,82 %, а для специальных трансформа-

торов

()

{}

(

)

0,0211 1,9479 exp 0,279ρν = − − ν (5.62)

с погрешностью менее 0,9 %.

Примем, что эти выражения справедливы и для ν ≤ 2. Это

позволяет получить искомые АЧФ в этих пределах путем деле-

ния (5.57) или (5.58) на (5.61) или (5.62): для цеховых трансфор-

маторов

()

{}

432

27,33 272,39 963,3 1452,8 855,66

1,9434 exp 0, 278

νϑ

ν− ν+ ν− ν+

ν=

−− ν

(5.63)

для специальных трансформаторов при ν от 0 до 1

()

{}

432

31,611 315,94 1111 1625,4 859,2

1,9479 exp 0,279

νϑ

ν− ν+ ν− ν+

ν=

−− ν

(5.64)

а от 1 до 2 – АЧФ определяется по формуле (5.63).

Коэффициент передачи определим из условия равенства

(5.64) единице при ν = 1:

{

}

()

1,9479 exp 0,279 859,2 0,001387.

k =−− =

В отличие от АЧФ на рис. 5.14, АЧФ фильтров в моделях

ЭМС по температуре для цеховых и специальных трансформа-

торов не совпадают во всем частотном диапазоне (рис. 5.15).

С учетом (5.43) найдем коэффициент

()

10 52 C % .

−

==°

Рассмотрим дополнительные потери мощности в ЛЭП.

Строго говоря, динамическая модель ЛЭП должна быть состав-

ной частью модели ЛЭП и электроприемника или группы элек-

Математические модели для оценивания параметров несинусоидальных режимов

195

троприемников, на вход которой подается несинусоидальная

компонента напряжения. Однако в силу малости сопротивления

ЛЭП по сравнению с сопротивлением электроприемников счи-

тают, что несинусоидальная компонента тока не зависит от со-

противления ЛЭП.

Так как влияние поверхностного эффекта обычно учиты-

вается в виде зависимости сопротивления ЛЭП от частоты,

удобно ввести соответствующую АЧФ А

(ν) по сопротивлению,

приняв за единицу ее значение при 50 Гц. В соответствии с

формулой (5.45) эта АЧФ получается заменой п на ν:

()

при 1.

=ν ν≥ (5.65)

0,2

0,4

0,6

0,8

1,2

012

0,02

0,04

0,06

0,08

0 2040608010

тνϑ

Рис. 5.15. АЧФ взвешивающих фильтров моделей ЭМС с ФНЧ

по температуре дополнительного перегрева от несинусоидально-

сти напряжения для трансформаторов: 1 – цеховых, 2 – специ-

альных

Здесь частотный диапазон расширен влево до 50 Гц, по-

скольку выражение (5.65) удовлетворяет условию нормировки:

при ν = 1 АЧФ равна единице. Распространять же (5.65) на час-

тоты менее 50 Гц невозможно, так как при

нулевой частоте по-

лучается нулевое значение, хотя должно быть омическое сопро-

тивление. Различием в омическом и активном сопротивлениях

на частотах менее 50 Гц можно пренебречь, что позволяет при-

нять

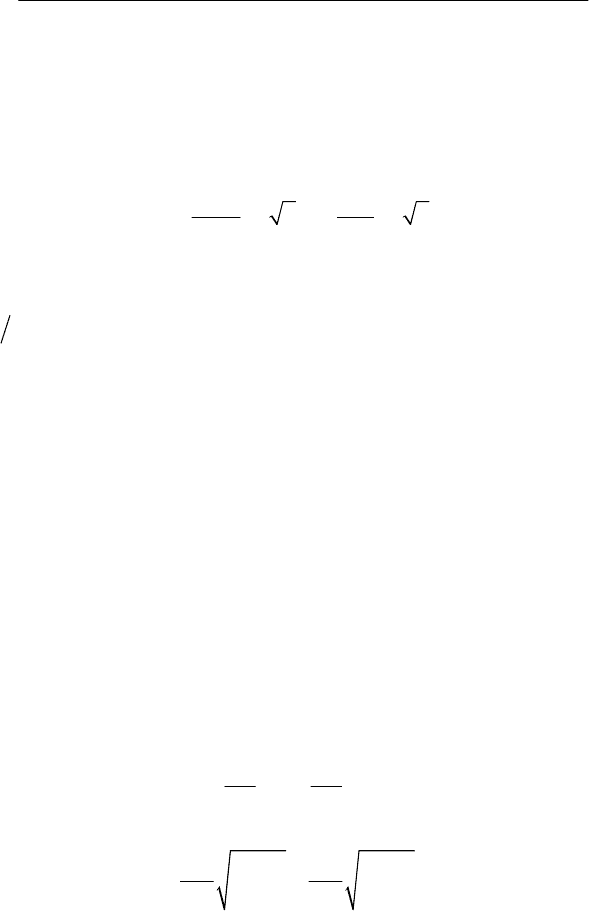
Раздел 5

196

(ν) = 1 при 0 ≤ ν ≤ 1.

Выразим потери в процентах от потерь в ЛЭП при проте-

кании длительно допустимого тока [I], которые равны

Тогда вместо (5.45) получим

[]

лэп

3.Ir

[] []

лэп

1,41 47

100 .

PnI

∞∞

∆= =

∑∑

nI (5.66)

Это означает, что коэффициент передачи

составляет

лэпP

∆

[]

()

47 , % A .I

−

⋅

5.7. Нормируемые показатели ЭМС по несинусоидальности

напряжения

Несинусоидальность напряжения во всех стандартах оце-

нивается по коэффициентам K

искажения синусоидальности

напряжения и K

п-ой гармонической составляющей, которые

для краткости будем именовать коэффициентами искажения и

гармоники. Как и для несимметрии напряжений, примем сле-

дующие обозначения: K

U[θ]

и K

Un[θ]

– среднеквадратические ко-

эффициенты искажения и гармоники за промежуток времени [θ]

= 3 с (в [6] – Т

νs

За интервал осреднения количество N наблюдений должно

быть не менее девяти. Результаты i-го наблюдения вычисляются

по формулам:

1 н

100 100,

ni ni

Uni

=≈

(5.67)

40 40

1 н

100 100

Ui ni ni

=≈

∑

(5.68)

В принятых обозначениях

Математические модели для оценивания параметров несинусоидальных режимов

197

[]

Uni

∑

(5.69)

[]

∑

(5.70)

Допустимые значения показателей несинусоидальности

напряжения из [6] приведены в табл. 5.2 и 5.3. Предельно допус-

тимые значения коэффициента гармоник принимаются в 1,5

раза бόльшими по сравнению с указанными в табл. 5.3.

Принцип нормирования по гармоникам принят в стандар-

тах других стран [65-71], а также в проектах стандартов Между-

народной электротехнической комиссии [

59-62]. Сопоставление

стандартов дано в [20, 73]. Некорректность такого принципа по-

казана в п. 5.1. Однако до уточнения стандартов контроль ЭМС

в точках коммерческого учета должен производиться по нормам

существующего стандарта.

Для достижения единства измерений и расчетов необхо-

димо иметь единую модель для выделения «гармоник» из поме-

хи. Как отмечалось в

п. 5.1, эта операция осуществляется про-

пусканием помехи через полосно-пропускающие фильтры ФПП,

настроенные на частоты канонических гармоник: от п= 2 до 40

(рис. 5.16). Реакции у

(t) фильтров возводятся в квадрат и опре-

деляются квадраты их действующих значений K

за цикл дли-

тельностью 0,02 с. Для периодической помехи величины K

являются коэффициентами гармоник, а для случайных – коэф-

фициентами псевдогармоник. Коэффициент искажения опреде-

ляется извлечением корня в звене 7 из суммы квадратов коэф-

фициентов гармоник.

В соответствии с (5.69) и (5.70) под стандартными следует

понимать электроприемники, осуществляющие квадратичное

трехсекундное осреднение. Их количество равно 40 – один для

коэффициента искажения и 39 – для коэффициентов гармоник.

Структурные схемы моделей (

рис. 5.17) аналогичны схеме на

рис. 3.8,а – отличие состоит только в индексах обозначений

энергетических кумулятивных процессов w

U[θ]

(t) и w

Un[θ]

(t) и ко-

Раздел 5

198

Таблица 5.2 – Нормируемые значения коэффициента ис-

кажения в процентах

кВ

Нормально допустимые Предельно допустимые

0,38 8 12

6-20 5 8

35 4 6

110-330 2 3

Таблица 5.3 – Нормируемые значения коэффициента гар-

моник в процентах для нормального режима

, кВ

0,38 6-20 35 110-330

5 6 4 3 1,5

7 5 3 2,5 1

11 3,5 2 2 1

13 3 2 1,5 0,7

17 2 1,5 1 0,5

19 1,5 1 1 0,4

23 1,5 1 1 0,4

≥ 25

0,2 + 32,5/п 0,2 + 20/п 0,2 + 15/п 0,2 + 5/п

3 2,5; 5

1,5; 3

0,75; 1,5

9 0,75; 1,5

0,5; 1

0,2; 0,4

15 0,3 0,3 0,3 0,2

≥ 21

0,2 0,2 0,2 0,2

2 2 1,5 1 0,5

4 1 0,7 0,5 0,3

6 0,5 0,3 0,3 0,2

8 0,5 0,3 0,3 0,2

10 0,5 0,3 0,3 0,2

≥ 12

0,2 0,2 0,2 0,2

Для однофазных электрических сетей

Математические модели для оценивания параметров несинусоидальных режимов

199

ФПП

(%)

…

ФПП

(%)

40U

…

U40

n = 2

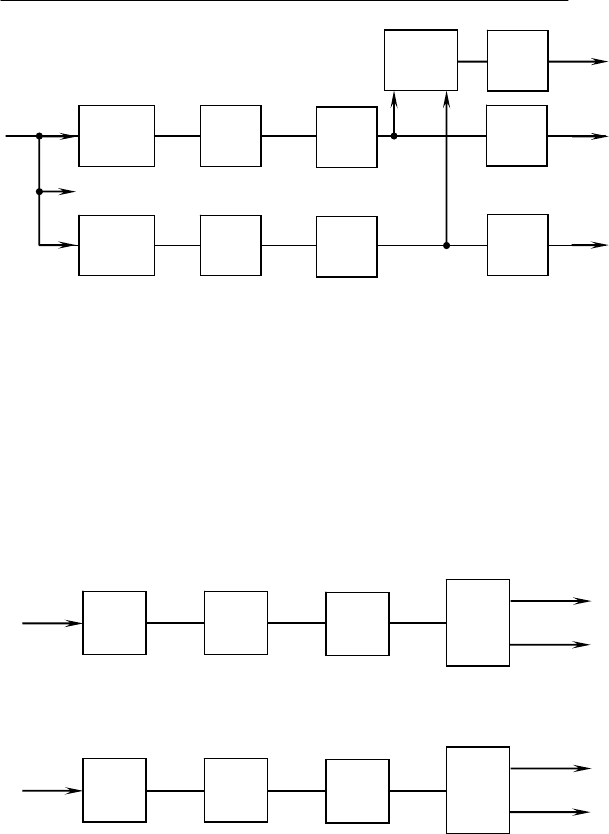
Рис. 5.16. Структурные схемы моделей для определения

текущих значений коэффициентов искажения и гармоник

эффициентов K

U[θ]

и K

Un[θ]

. В блоках 8 с интегральной вероятно-

стью 0,95 определяются максимальные значения K

U[θ]нmax

для

нормального режима и с вероятностью 0,999 – значения K

U[θ]пmax

для предельного режима. Они не должны превосходить норми-

руемые значения, приведенные в табл. 5.2 и 5.3.

(%)

U[θ]

(%)

U[θ]

U[θ]н max

U[θ]п max

2Un

(%)

Un[θ]

(%)

Un[θ]

Un[θ]н max

Un[θ]п max

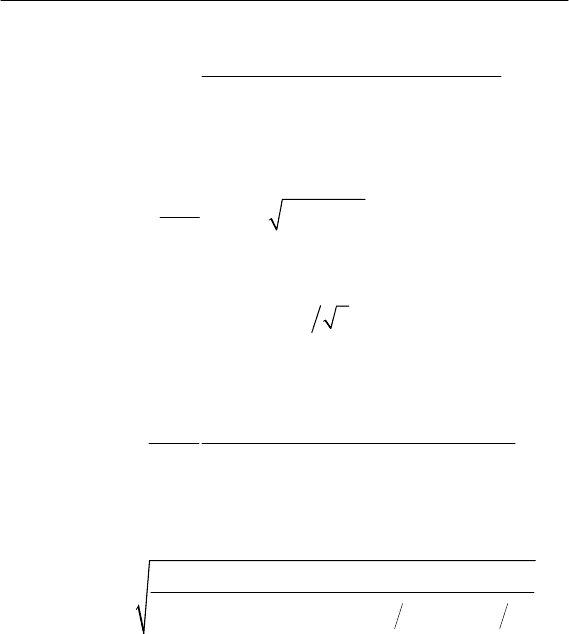
Рис. 5.17. Структурные схемы стандартных электропри-

емников по несинусоидальности напряжения: а – для коэффици-

ента искажения, б – для коэффициентов гармоник (2 ≤ п ≤ 40)

Раздел 5

200

Как и при оценивании несимметрии (рис. 3.8,б), вместо

трехсекундного осреднения целесообразно перейти к квадра-

тичному инерционному сглаживанию. В этом случае в схемах

на рис. 5.17 кумулятивное звено 3 заменяется на инерционное

звено 2 с постоянной времени 1,3 с.

Дальнейшее совершенствование нормирования будет идти

по пути реализации принципа нормирования по дозам (п. 1.9). В

действующих сетях помехи

могут иметь широкий частотный

диапазон (рис. 5.3). В низкочастотном диапазоне несинусои-

дальность напряжения более всего сказывается на электропри-

емниках с индуктивной проводимостью, а в высокочастотном –

на конденсаторных установках и изоляции. Поэтому надо ввести

два стандартных электроприемника и две дозы несинусоидаль-

ности: ψ

νl

– низкочастотную и ψ

νh

– высокочастотную. Выбор

стандартных электроприемников и их параметров должен осу-

ществляться путем экспертных оценок, что требует отдельного

рассмотрения.

При нормировании высокочастотной дозы в качестве

стандартного объекта естественно принять силовой конденсатор

со схемой замещения без релаксаторов. Для учета ограниченно-

сти частотного диапазона в схему ВФ (рис. 5.8) введем ФНЧ.

Структура такого составного ВФ

представлена на рис. 5.18. На

выходе ВФ протекает ток i

Cν

, который практически не отличает-

ся от тока КУ в схеме без ФНЧ. Для определенности стандарт-

ным будем считать силовой конденсатор КМ-0,38-26-3УЗ, пара-

метры которого приведены в п. 5.4.

Сν

ФНЧ

Рис. 5.18. Структурная схема ВФ в модели ЭМС стан-

дартного конденсатора с ФНЧ

Перемножая выражения (5.21) и (5.46), получим переда-

точную функцию

Математические модели для оценивания параметров несинусоидальных режимов

201

()

22 2 2

11 10 Б2 Б1

Wpk

Tp Tp T p Tp

+++

(5.71)

Полюса многочлена во вторых скобках:

(

)

()

Б1,2 Б1 Б1 Б2 Б

Б2

TTT j

=−±−=−α∓

где

Бп

2.α=ω

С учетом (5.23) представим (5.71) в виде

()

()()( )( )

Б211 1 2 Б1 Б2

kTp

TT pp pp pp pp

−−− −

(5.72)

Произведение выражений (5.24) и (5.47) дает АЧФ

()

() ()

22 22 2 2 2 2

11 10 пп

+ω

ω=

⎡⎤

−

ω+ω −ωω+ωω

⎣⎦

(5.73)

Допустимую температуру

[

]

∆

дополнительного пере-

грева КУ от несинусоидальности напряжения можно установить

либо из условия допустимой перегрузки, либо из допустимого

сокращения срока службы.

Стандарт [5], как и [41], допускает длительную работу КУ

при нагрузках до 1,3 от номинального тока. Тем не менее при-

нимать значение 1,3 в качестве длительно допустимого нельзя,

так как

в этом же стандарте повышение напряжения, а следова-

тельно тока, на 30 % допускается лишь в течение 10 мин. В ка-

честве экспертной оценки длительно допустимую перегрузку

можно принять равной 10 %, что соответствует норме повыше-

ния напряжения на 10 %, которое допускается в течение 12 ч,