Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

Раздел 5

172

тельные потери ∆Р

νс

активной мощности и кратность γ

zν

сниже-

ния срока службы изоляции.

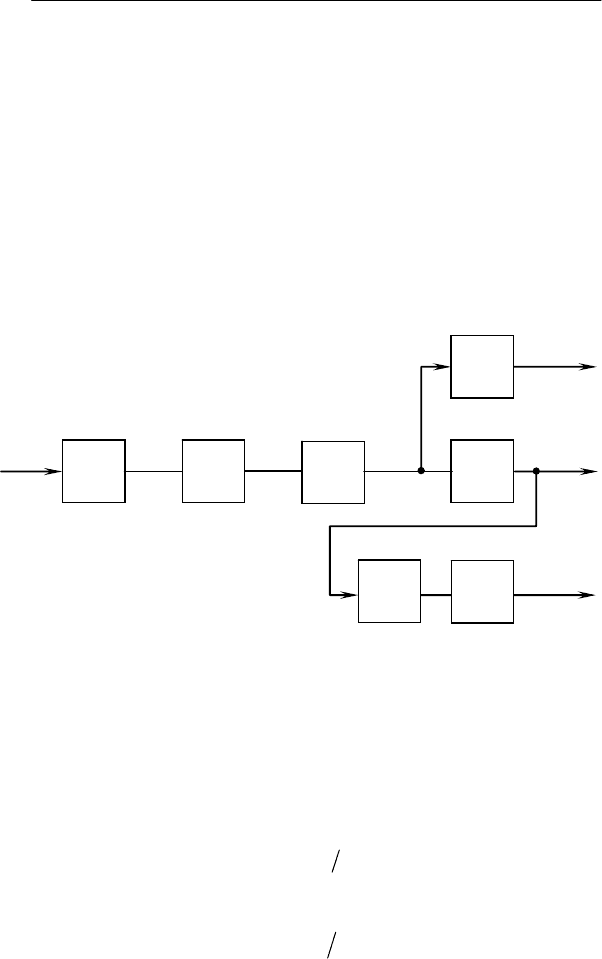
Структурная схема динамической модели ЭМС (рис. 5.6)

аналогична схеме на рис. 3.6,а для несимметрии напряжений. В

ней роль ВФ, моделирующего несинусоидальную компоненту i

тока двигателя, выполняет инерционное звено 2 с коэффициен-

том передачи а

дν

и постоянной инерции Т

дν

. Схема же на рис.

3.6,б не может быть аналогом (с заменой коэффициента несим-

метрии на коэффициент искажения), поскольку в ней отсутству-

ет ВФ.

(%)

ϑi

∆Рi

(%)

∆

кВт

∆

°С

о.е.

zν

Рис. 5.6. Структурные схемы динамических моделей ЭМС

электродвигателей по несинусоидальности напряжения

Коэффициенты передачи пропорциональных звеньев 4 для

оценивания температуры определяются выражениями, стоящи-

ми перед суммами в формулах (5.7) и (5.9): для АД

0,03892 ,

(5.13)

а для СД

см

10 .

−

′

(5.14)

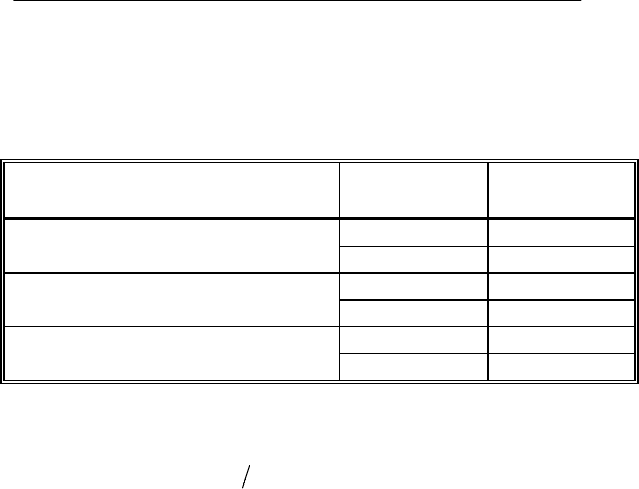
Математические модели для оценивания параметров несинусоидальных режимов

173

Рассчитанные по этим формулам значения коэффициентов

для изоляции классов А и В приведены в табл. 5.1.

Таблица 5.1 – Коэффициенты передачи для вычисления

температур дополнительного перегрева двигателей

Двигатель

Класс

изоляции

ϑi

°С

(%)

0,449

АД

0,562

0,782

СД с успокоительной обмоткой

0,977

0,312

СД без успокоительной обмотки

0,389

Произведения перед суммами в формулах (5.8) и (5.10)

выражены в процентах. Для перехода к потерям мощности в кВт

их надо умножить на

100.P

В результате для АД получим

(5.15)

АД н

210 ,

−

∆

=⋅ P

а для СД –

от н

10 .

−

∆

′

= (5.16)

С учетом выражений для k

АД

(п. 3.3) для АД найдем

452

нн н

нн

910 610 при 5кВт,

2,105 10 1,79 10 при 5100кВт,

0,01333 6,67 10 при 100 1000 кВт.

PP P

cPP

−−

∆

−

⎧

⋅−⋅ ≤

⎪

=⋅+⋅ ≤≤

⎨

⎪

+⋅ ≤≤

⎩

(5.17)

Подстановка в (5.16) численных значений

от

′

для СД с

успокоительной обмоткой и без нее дает коэффициенты переда-

чи 8, 68⋅10

–5

и 3,46⋅10

–5

, кВт

(%)

Раздел 5

174

5.4. Динамические модели ЭМС конденсаторных установок

по несинусоидальности напряжения для оценивания

тепловых эффектов

Входная проводимость КУ уменьшается с увеличением

частоты напряжения. Для частного случая периодических помех

в виде суммы высших гармоник температура дополнительного

нагрева КУ определяется по формуле [51, 53]

10 ,

∞

−

∆ϑ = ϑ

∑

где ϑ

– температура перегрева при номинальном синусоидаль-

ном напряжении, которую рекомендуется принимать равной

30°С. В этом случае

(5.18)

0,003 ,

∞

∆ϑ =

∑

где коэффициент перед суммой имеет размерность °С

(%)

Дополнительные потери активной мощности в кВт

(5.19)

10 tg ,

PQ nK

∞

−

∆= δ

∑

где Q

– номинальная мощность КУ в квар, δ – угол потерь.

В отличие от моделей электродвигателей структуру ВФ

нельзя выбирать путем распространения формул (5.18) и (5.19)

на общий случай непрерывных значений частот ν, так как при

п → ∞ они дают бесконечность, что противоречит физическому

смыслу. Кроме того, в формуле (5.19) тангенс потерь считается

неизменным, что

справедливо лишь для частного случая непо-

лярных диэлектриков (полиэтилен и др.)

Структуру ВФ, который моделирует несинусоидальную

компоненту тока i

Cν

, примем согласно схеме замещения КУ [15],

приведенной на рис. 5.7. Металлические части конденсатора

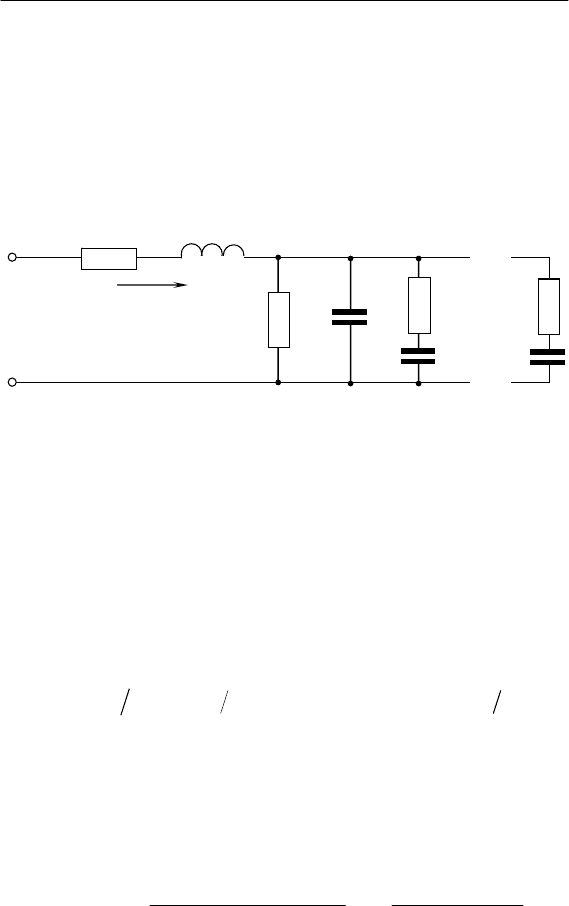
Математические модели для оценивания параметров несинусоидальных режимов

175

моделируются активным сопротивлением r и индуктивностью L,

не зависящими от частоты. Диэлектрик моделируется парал-

лельно включенными цепями. Две первые из них содержат со-

противление r

и геометрическую емкость С, остальные т ре-

лаксаторов – последовательно включенные сопротивления и ем-

кости. Модель учитывает зависимость угла потерь от частоты.

Сν

…

Рис. 5.7. Схема замещения конденсаторной установки

На рис. 5.7 не показаны активное сопротивление и индук-

тивность сети от шин подстанции до зажимов КУ. Они учиты-

ваются путем добавления к r и L. Разрядные сопротивления

практически не сказываются на переходных процессах в КУ.

Структуру ВФ в динамической модели ЭМС найдем та-

ким же путем

, как и в модели двигателя (п. 3.7). Введем обозна-

чения:

()

0007080

9 00 1089 1178

11, ,

grrrTrCTgLL

TgrCrC T TT T TTLC

=+≈ = =≈

=≈ =+ =≈

где учтено, что

.rr

При отсутствии релаксантов эквивалентная проводимость

()

222

78 8 9 11 10

() .

Tp Tp

Yp g g

TT p T T p T p T p

++ ++

(5.20)

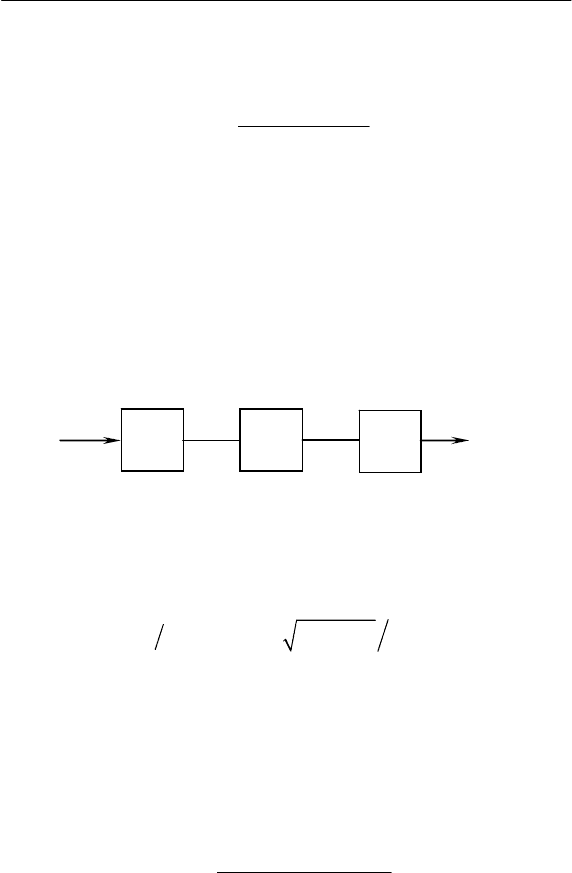
Раздел 5

176

Передаточная функция ВФ по току получается умножени-

ем проводимости на номинальное сопротивление z

Cн

КУ:

11 10

() .

Wp k

Tp Tp

(5.21)

Здесь коэффициент передачи

выражен в о.е.

0 нC

kgz=

Согласно (5.21) ВФ включает в себя пропорциональное

звено 4 с коэффициентом передачи k

, колебательное звено 9 с

постоянными времени Т

и Т

, а также форсирующее звено 10 с

постоянной времени T

(рис. 5.8). На выходе ВФ протекает ток

КУ в процентах от его номинального значения.

Сν

Рис. 5.8. Структурная схема ВФ по току КУ

Обозначив через

222

10 11 11 10 11

2, 4 2

TT TTTα= λ= −

найдем полюса

1,2 C

−α ± λ

(5.22)

знаменателя передаточной функции и запишем ее в виде

()()

11 1 2

() .

Wp k

Tpppp

−−

(5.23)

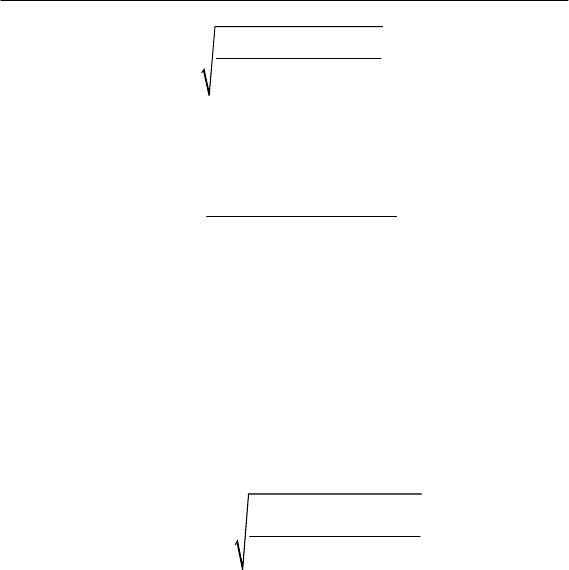
Передаточной функции соответствует АЧФ

Математические модели для оценивания параметров несинусоидальных режимов

177

()

22 22

11 10

() при

+ω

=ω

−ω +ω

≥

(5.24)

и фазочастотная функция

()

(

)

71110

arctg при 0,

TTT

⎡⎤

ω−ω−

⎣⎦

ϕω= ω>

+ω

(5.25)

где

12 7 9 0 7 10 11

.TTTrrCTTT== = −

Номинальное сопротивление найдем из условия равенства

АЧФ единице при угловой частоте ω

синусоидального напря-

жения:

()

22 22

11 10

н 0

−ω +ω

+ω

(5.26)

Следует отметить, что сопротивление, вычисленное по

номинальным значениям реактивной мощности и напряжения,

несколько отличается от (5.26).

В отличие от идеального конденсатора, АЧФ которого

представляет собой выходящую из нуля неограниченно возрас-

тающую прямую, АЧФ реального конденсатора при нулевой

частоте равна коэффициенту передачи, поскольку напряжение

постоянного тока создает ток утечки. В зоне частот

примерно до

5000 Гц АЧФ возрастает почти линейно, так как индуктивность

металлических частей из-за ее малости практически не сказыва-

ется на токе КУ. При дальнейшем увеличении частоты происхо-

дит быстрое возрастание АЧФ. Резонансный максимум достига-

ется при частоте

Раздел 5

178

ез 10 7

1TT

ω= − ,

(5.27)

при которой выражение (5.24) обращается в нуль. До резонанса

ток КУ является емкостным, а после – индуктивным. При уве-

личении частоты свыше резонансной АЧФ уменьшается вначале

быстро, а потом медленнее, стремясь к нулю.

Поскольку помеха измеряется в процентах от номиналь-

ного напряжения, переходная функция представляет собой пе-

реходный ток в процентах от

номинального тока КУ, который

возникает в результате воздействия на ВФ произведения еди-

ничной функции 1(t) на напряжение и

= 1 %. Она может быть

определена по таблицам обратного преобразования Лапласа:

()

() .

ht uL W p

−

⎧

⎫

⎨

⎬

⎩⎭

Однако в рассматриваемом случае проще воспользоваться

известными формулами для переходной h

(t) и весовой g

(t)

функций колебательного звена [49]. В соответствии с рис. 5.8

процесс после звена 9 поступает на форсирующее звено, на вы-

ходе которого протекает сумма двух процессов: входного и его

производной с коэффициентом Т

. Поэтому

(

)

(

)

(

)

к 7 к

ht ht T

t=+

(5.28)

Обозначив через

() ()

12 1 , arcsin1

CCC

aTT

=−α− ϕ=

и используя выражение (5.23), получим

{

}

(

)

() 1 exp sin ,

CC CCC

ht ku a t t

⎡− −α λ +ϕ ⎤

⎣

⎦

Математические модели для оценивания параметров несинусоидальных режимов

179

{}

() exp sin ,

tku t t

−α λ

где учтено соотношение

711 8

1.TT T=

Идеальный же конденсатор имеет переходную функцию

(

)

() .

ht uC t

=δ

(5.29)

В качестве примера приведем данные силового конденса-

тора КМ-0,38-26-3УЗ из [32]: напряжение 380 В, мощность 26

квар, емкость 5,84⋅10

–4

Ф, индуктивность 2,7⋅10

–7

Гн, сопротив-

ления r

= 2,69⋅10

и r = 6,88⋅10

–3

Ом. В этом случае постоянные

времени Т

= 1,571⋅10

, Т

= 4,018⋅10

–6

и Т

= 1,256⋅10

–5

с, про-

водимость g

= 3,718⋅10

–9

См, номинальное сопротивление 5,46

Ом, коэффициент передачи k

= 2,03⋅10

–8

. Расчет по номиналь-

ным данным дает индуктивное сопротивление 5,554 Ом – на

1,42 % больше, чем 5,46 Ом. АЧФ этого конденсатора имеет ре-

зонансный максимум на частоте 12672 Гц. Переходная функция,

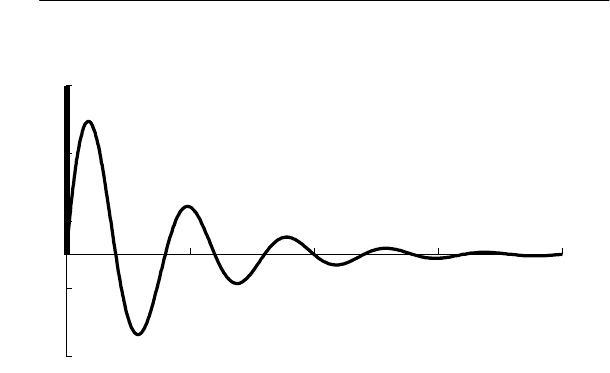
рассчитанная по формуле (5.28), представлена на рис. 5.9, где

для сравнения утолщенной линией показана переходная харак-

теристика (5.29), уходящая в бесконечность.

Введение релаксаторов усложняет передаточную функ-

цию: порядок

многочлена в ее числителе становится равным

т + 1, а знаменателя – на единицу больше. Например, при од-

ном релаксаторе с постоянной времени Т

р1

= R

вместо (5.20)

получим эквивалентную проводимость

13 14

33 22

15 16 17

() ,

Tp Tp

Yp g

Tp Tp Tp

где

13 7 р1147р101 15 11р1

01 0 1

10 16 р10117018р1

,,,

TTT TTTrCTTT

C C C T R T rCT LC T rC T T

==++=

=++ = + = ++.

Раздел 5

180

Рис. 5.9. Переходная характеристика силового конденсатора

26 квар, 380 В

-150

-50

150

250

0 0,1 0,2 0,3 0,4

% h

t, мс

Записав выражения для передаточных функций при одном

и двух релаксаторах, магистр Майоров А.Л. сформулировал ал-

горитм написания аналитических выражений при любом т. Од-

нако в практических расчетах даже при т = 2 целесообразно ис-

пользовать пакет Matlab для нахождения численных значений

коэффициентов многочленов и

полюсов знаменателя, а затем

применить метод парциальных реакций.

Далее для краткости рассматривается схема замещения

без релаксаторов, но все методы оценивания ЭМС очевидным

образом распространяются на схемы замещения с любым коли-

чеством релаксаторов.

Постоянные времени нагрева силовых конденсаторов пре-

вышают 1 ч [47], поэтому оценивание температуры достаточно

выполнить по ее среднему

значению, пропорциональному квад-

рату эффективного ток i

Cνэ

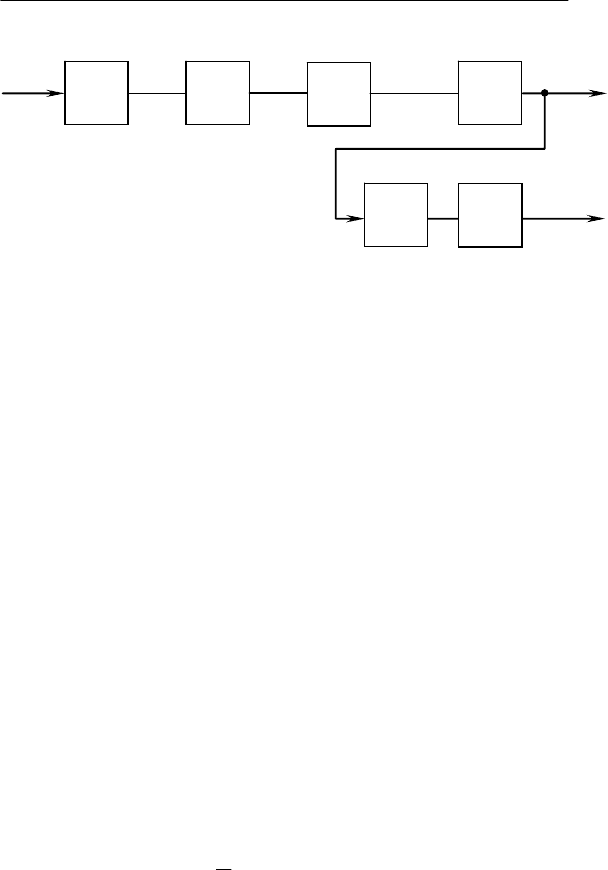
. В связи с этим динамическая модель

ЭМС (рис. 5.10) будет иметь те же структурные элементы, что и

модель двигателей на рис. 5.6. Согласно (5.18) коэффициент пе-

редачи с

Сνi

= 0,003°С

(%)

, т.е. совпадает с (3.26).

Математические модели для оценивания параметров несинусоидальных режимов

181

ВФ

Сν

(%)

эC

(%)

∆

°С

о.е.

zν

Сϑi

Рис. 5.10. Структурные схемы динамических моделей ЭМС

КУ по тепловым эффектам

5.5. Динамические модели ЭМС конденсаторных установок

по несинусоидальности напряжения для оценивания

потерь мощности

Средние потери активной мощности ∆Р

равны значению

в нуле взаимной корреляционной функции между процессами

на входе и выходе ВФ. Эта функция определяется по корреля-

ционной функции В

(τ) помехи [22]:

()

()()

ui C

∞

=τ+ξξ

∫

ξ (5.30)

где весовая функция g

(t) получается дифференцированием вы-

ражения (5.28) по времени. Следует отметить, что здесь аргу-

мент τ + ξ можно заменить на τ – ξ.

Весовая и передаточная функции связаны между собой

соотношением

()

{}

() Re cos ,

gt W j td

∞

ωω

∫

ω (5.31)

подстановка которого в (5.30) с учетом (1.6) дает