Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

152 Раздел 4

сдвинутые по фазе напряжения U

и U

. В связи с этим необхо-

димо суммировать проекции токов симметричных составляю-

щих. Среднее значение тока ЛЭП в амперах

()

12 12xx yy

III II

ΣΣΣΣΣ

=+++

и дисперсия в А

11 2 2

yxy

IDI DI DI DI

ΣΣΣ Σ

+++

выражаются через суммы средних значений и дисперсий проек-

ций симметричных составляющих.

Обозначив через

222

1,2э 1,2 1,2 1,2 1,2

IIIDIDI

ΣΣ Σ

=++ +

получим выражение для квадрата эффективного тока

(

)

22 2

э 1э 2э 12 12

xx yy

II I II II

ΣΣΣ ΣΣΣΣ

=++ +

Согласно (1.43) коэффициент разделения для обратной

последовательности

2э

1э 2э

ρ=

Дополнительные потери активной мощности в ЛЭП от не-

симметрии напряжений вычисляются по величине

(

)

2э 2э 21 2 1 2

xx yy

II II II

ΣΣΣΣ

=+ρ + .

(4.69)

Перейдем к общему случаю, когда ВФ представляет собой

динамическую систему. В соответствии с методом парциальных

реакций (п. 2.2) ее можно представить в виде параллельно

Методы расчета показателей ЭМС по несимметрии напряжений 153

включенных инерционных звеньев. Для краткости рассмотрим

ВФ модели АД с передаточной функцией (3.37), который со-

держит два таких звена. Будем их нумеровать римскими цифра-

ми I и II.

График помехи задается в виде дискретной последова-

тельности ординат с малым шагом ∆, а ток рассчитывается по-

шагово. Первая ордината принимается равной нулю. Для каждо-

го

звена последующая r-я ордината при r ≥ 1 по аналогии с

(2.54) вычисляется с учетом предыдущей:

(

)

(

)

2I,II I,II 2 I,II ф 2

() 1 (),

Ir bIr baKr

∆

=∆−∆+− ∆

}

(4.70)

где

Результаты расчетов суммируются

{

I,II 1,2

exp .b =−γ∆

()

(

)

(

)

2 I II 2 I II ф 2

() 2 ()

Ir b b I r b baK r∆= + ∆−∆+ − − ∆. (4.71)

Если не учитывать контур намагничивания, то ток рассчи-

тывается по формуле (4.70), в которой

ф 1I

и используется

только величина

.γ

Исходные данные могут задаваться не графиком помехи, а

его характеристиками: средним значением

и корреляцион-

ной функцией

2 сU

(

)

Для ВФ в виде инерционного звена доста-

точно знать только эффективное значение коэффициентов не-

симметрии, по которому вычисляются показатели ЭМС, в том

числе и доза (3.53).

Среднее значение тока определяется сразу – по формуле

2сф2 э

IaK

(4.72)

Парциальные токи

I,II

на выходе инерционных звеньев яв-

ляются коррелированными, так как на их входы подается один и

тот же процесс. Их дисперсии определяются согласно (2.61):

{}

()

2I,II 1,2 1,2 1,2 2

exp .DI a B d

∞

γ−γττ

∫

τ (4.73)

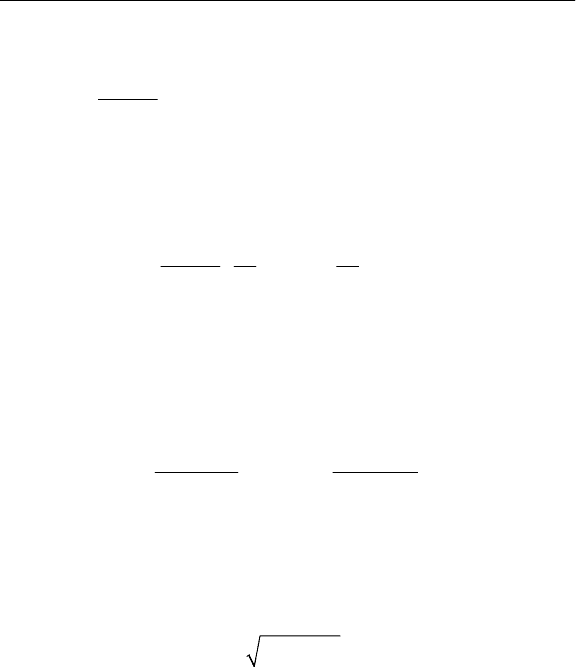
154 Раздел 4

Корреляционный момент связи между токами [12]

{} {}

(

()

III 1 2 1 2 2

exp exp .

)

aa B d

∞

γγ

=−γτ+−γτ

γ+γ

∫

ττ

(4.74)

Выразим из (4.73) интегралы через дисперсии и подставим

их в (4.74). В результате получим

III 2 2I 1 2II

121 2

BDI

⎛

=γ+γ

⎜

γ+γ

⎝⎠

⎞

⎟

(4.75)

С учетом (2.72) дисперсия суммы двух коррелированных

парциальных токов составит

() ()

22I2IIIII

22 11

2I 2II

11 2 21 2

DI DI DI B

DI DI

=+ + =

γγ

⎡⎤⎡⎤

=+ ++

⎢⎥⎢⎥

γ+γ γ+γ

⎣⎦⎣⎦

(4.76)

Выражения для инерционных дисперсий приведены в

табл. 2.2.

Эффективное значение

2е 2с 2

.IIDI=+

(4.77)

Для модели без контура намагничивания в (4.77) подстав-

ляется только одна дисперсия, которая рассчитывается согласно

(4.73) по

и γ

Дополнительные потери активной мощности в кВт опре-

деляются согласно (3.35) по величине эффективного тока в ам-

перах:

(4.78)

22э 2

310PIr

−

∆= ⋅

где

выражается в омах.

Методы расчета показателей ЭМС по несимметрии напряжений 155

С учетом (1.33) найдем среднюю температуру дополни-

тельного нагрева ЛЭП в °С

[]

22э

,II∆ϑ = ϑ (4.79)

где квадратными скобками отмечены длительно допустимые

температура и ток. Кратность снижения срока службы ЛЭП оп-

ределяется по формуле (1.37).

4.9. Технико-экономическая эффективность уменьшения

несимметрии напряжений

Полученные данные о показателях несимметрии исполь-

зуются для обоснования применения устройств уменьшения не-

симметрии напряжений. Техническая необходимость в этом

возникает, если нарушаются требования стандартов. Экономи-

ческая целесообразность доказывается путем сопоставления

эффекта от уменьшения дополнительных потерь электроэнергии

и увеличения срока службы электрооборудования с затратами

на устройства стабилизации.

Виды корректирующих устройств описаны

в [53], где да-

ны основы методов расчета сетей с такими устройствами. В об-

щем случае входящие в соответствующие формулы параметры

режима следует рассматривать как случайные процессы. Де-

тальный анализ эффективности корректирующих устройств

здесь не приводится. Ограничимся лишь простым примером.

Пусть от сети питается несимметричная трехфазная на-

грузка: например, установка

точного литья с емкостно-

индуктивным преобразователем [1]. Соответствующая схема

замещения включает в себя три источника тока, к которым под-

ключены соединенные в треугольники эквивалентные сопро-

тивления сети и плечей преобразователя. Так как токи различ-

ны, напряжения между вершинами треугольников будут разны-

ми, а они как раз и являются несимметричными

компонентами

напряжений для остальных электроприемников (точки

а и b на

рис. 2.1). Если подключить еще и треугольник сопротивлений

корректирующего устройства, подобранных таким образом,

156 Раздел 4

чтобы эквивалентные сопротивления всех трех треугольников

были одинаковы, то несимметрия напряжений будет устранена,

хотя несимметричная нагрузка установки остается без измене-

ния.

Для каждого вида электрооборудования ежегодный эко-

номический ущерб от несимметрии напряжений в грн/год опре-

деляется по формуле [53]

2 эо э 2 р

нн

УЗ з ,

γ−

⎛⎞

⎜⎟

⎝⎠

∆

(4.80)

где З

эо

– приведенные затраты на оборудование, Т

– число часов

работы оборудования в году,

– номинальный срок службы, з

– стоимость 1 кВт⋅ч потерь электроэнергии,

– нормативный

коэффициент эффективности капиталовложений, который явля-

ется величиной, обратной нормативному сроку окупаемости.

Корректирующее устройство стоимостью К

кор

с ежегод-

ными эксплуатационными издержками уменьшает ущерб на ве-

личину ∆У

, зависящую от остаточной несиметрии напряжений.

Срок окупаемости корректирующих устройств (в грн)

кор

2 кор

УИ

T =

∆−

(4.81)

Экономический эффект от применения корректирующего

устройства (в грн

год)

= ∆У

– И

кор

– Е

кор

. (4.82)

Эта величина будет больше нуля, если срок окупаемости

положителен и не превышает 1/

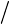
Раздел 5

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ОЦЕНИВАНИЯ

ПАРАМЕТРОВ НЕСИНУСОИДАЛЬНЫХ РЕЖИМОВ

5.1. Несинусоидальные компоненты

Как и несимметрия напряжений (п.3.1), искажения кривой

напряжения могут быть вызваны как внешними, так и внутрен-

ними причинами. Внешние искажения обусловлены несинусои-

дальностью ЭДС генераторов электростанций, а также мощны-

ми нелинейными нагрузками на соседних предприятиях. Источ-

никами внутренних искажений являются мощные электропри-

емники с нелинейными вольт-амперными характеристиками

(тиристорные преобразователи, ДСП, насыщенные магнитные

системы и др.). При экспериментальных исследованиях учиты-

вается совместное воздействие внешних и внутренних искаже-

ний. В проектировании напряжение источника питания считает-

ся неискаженным.

Поскольку электроэнергия передается на частоте f = 50 Гц,

процесс u(t) изменения текущих значений напряжения естест-

венно представить в виде суммы двух компонент

: синусоидаль-

ной u

(t) с частотой 50 Гц и несинусоидальной

() () (),

ut ut u t

−

(5.1)

которые будем называть синусоидой и помехой.

Вопрос выделения синусоиды является ключевым для

трактовки самого понятия несинусоидальности. Рассмотрим

вначале случай периодической помехи с длительностью цикла

10,0

tf==2

с, которая накладывается на синусоиду

() sin

ut B t

(5.2)

с амплитудой В

, той же длительностью цикла и несущей угло-

вой частотой

ω=π

Раздел 5

158

По смыслу синусоидальная компонента совпадает с (5.2).

Однако синусоиду можно выделить и методом наименьших

квадратов, что в этом частном случае равносильно использова-

нию формул для коэффициентов ряда Фурье. Тем самым напря-

жение представляется в виде суммы

() () ()

ut u t u t

ΦΣ

(5.3)

первой (основной) гармоники

и суммы канониче-

ских гармоник с порядком п ≥ 2.

()ut

()

Таким образом, для периодической помехи возможны две

трактовки несинусоидальности: как разность (5.1) или как сум-

ма высших гармоник. Подставив (5.3) в (5.1), получим соотно-

шение

() () () ().

ut u t u t ut

νΦΣ

+−

Отсюда следует, что несинусоидальная компонента сов-

падает с суммой высших гармоник лишь при равенстве

которое выполняется далеко не всегда. Проиллюстрируем

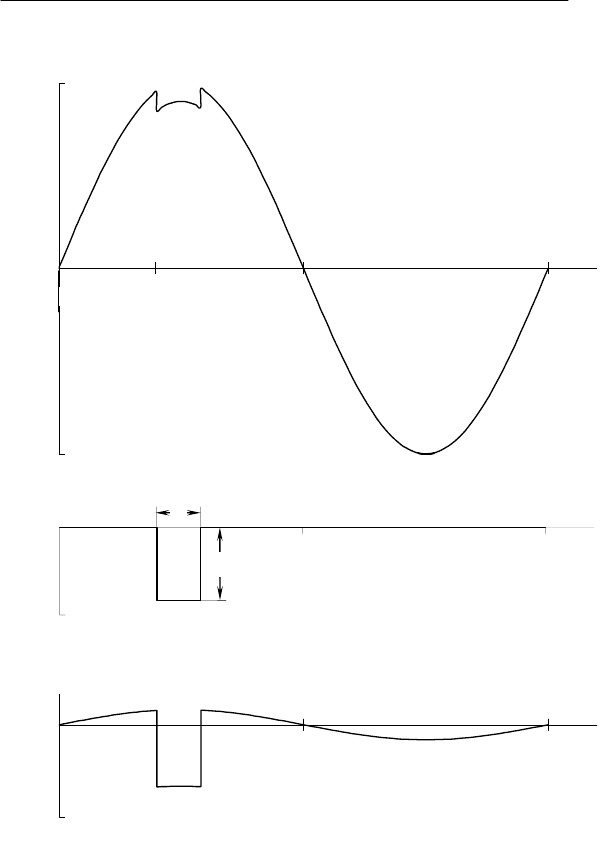
это на следующем примере. Пусть в каждом цикле синусоиды

источник помехи в положительной полуволне создает провал

прямоугольной формы глубиной В и шириной θ, середина кото-

рого приходится на вершину синусоиды (рис. 5.1,а), где t

()ut

(),

– мо-

мент начала провала.

При первой трактовке несинусоидальности график помехи

имеет вид, показанный на рис. 5.1,б. Амплитуда же основной

канонической гармоники не совпадает с В

, а определяется вы-

ражением

()

sin 2 1 sin

ff f f

BB B B B

Φ∗

⎛⎞

∗

−ωθ=−π

⎜⎟

ππ

⎝⎠

θ (5.4)

при

∗

θ=θ

∗

а фаза равна нулю. В общем случае

амплитуда и фаза зависят от положения провала.

Математические модели для оценивания параметров несинусоидальных режимов

159

-1

00,010,02

-0,12

0,01 0,02

–

-0,12

00,01

0,02

nΣ

Рис. 5.1. Выделение из помехи (а) несинусоидальной ком-

поненты: б – по неискаженной части синусоиды, в – вычитанием

первой гармоники

Раздел 5

160

Вычитанием основной гармоники из исходного процесса

получим график суммы

() () ()

ut ut ut

ΣΦ

−

высших гармоник (рис. 5.1,в), который принципиально отлича-

ется от несинусоидальной компоненты на рис. 5.1,б: «помеха»

якобы имеется в продолжении всего цикла и вызывается двумя

провалами (отрицательные области) и двумя выбросами (поло-

жительные области), хотя в действительности есть только один

провал.

В проектировании, когда задан график помехи (5.1), легко

реализуются обе трактовки

несинусоидальности. В действую-

щих сетях выделить синусоиду (5.2) можно, если кривая напря-

жения имеет четко выраженные неискаженные участки сину-

соиды. На этих участках определенные по любым парам орди-

нат параметры синусоиды остаются неизменными. Несинусои-

дальная компонента определяется согласно (5.1). При отсутст-

вии неискаженных участков задача выделения синусоиды не

имеет точного решения. В связи

с этим необходимо оценивать

влияние на электрооборудование всего процесса u(t) или в каче-

стве несинусоидальной компоненты ориентировочно принимать

сумму высших гармоник, если помеха периодична. Несоответ-

ствие между несинусоидальной компонентой и суммой высших

гармоник наглядно проявляется, если периодическая помеха

имеет длительность цикла, отличающуюся от 0,02 с. Например,

пусть провал появляется не

в каждом цикле синусоиды, а только

в одном из N циклов. В этом случае длительность цикла помехи

равна Nt

. Вычитание неискаженной синусоиды дает правиль-

ный график помехи: один провал за время Nt

. График же суммы

высших гармоник будет наблюдаться все это время: провал, как

и первая гармоника, как бы разносится на весь цикл. Чтобы это-

го не произошло, целесообразно выделять синусоиду в каждом

цикле – для рассматриваемого примера только в одном цикле

будет сумма высших гармоник (рис. 5.1,в), а в остальных циклах

искажения

отсутствуют.

Недостатком поцикличного выделения первой гармоники

является то, что на границах участков длительностью t

ордина-

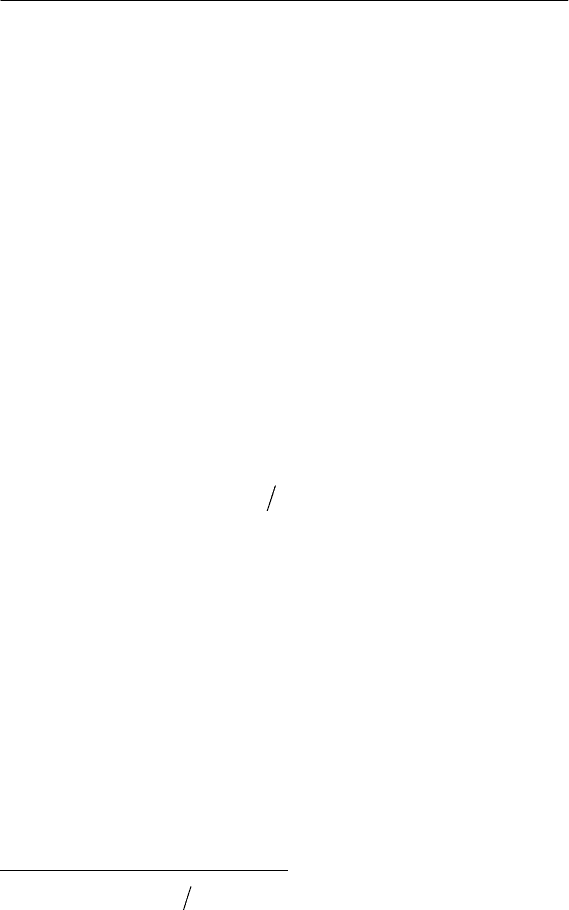
Математические модели для оценивания параметров несинусоидальных режимов

161

ты смежных синусоид могут не совпадать. Это объясняется тем,

что каждый отдельно взятый цикл считается бесконечно повто-

ряющимся, хотя это не так. Например, если в одном цикле сину-

соиды провал будет смещен относительно синусоиды, то ее фаза

не будет равна нулю, а потому на границах цикла ординаты бу-

дут отличаться от

нуля, хотя по условию в предыдущих и по-

следующих N – 1 циклах t

синусоида проходит через нуль на

границах участков. По этой причине на границах участков сле-

дует принимать полусумму ординат или, что удобнее, в каждом

цикле t

рассчитывать синусоиду от 0 до t

– ∆.

Перейдем к непериодическим помехам. Теоретически они

задаются на бесконечном интервале времени, когда понятие

гармоники отсутствует и говорить о сумме высших гармоник

некорректно. В практике, как искусственный расчетный прием,

используется представление непериодических процессов в виде

ряда Фурье на конечном интервале Т

(в [6] – 0,32 с). Тем самым

предполагается, что до и после рассматриваемого интервала

процесс периодически повторяется с длительностью цикла Т

основной частотой

2T .

=π

Обозначим порядок слагаемых

ряда через µ и назовем их «квазигармониками». Такой прием

возможен, если требуемая для решения задачи длительность

процесса меньше периода разложения Т

Обычно длительность t

целое число т раз укладывается

на интервале разложения, поэтому основная квазигармоника

имеет частоту в т раз меньшую 50 Гц. По отношению к 50 Гц

квазигармоники с порядком

воспринимаются наблюда-

телем как канонические гармоники, а с другими порядками –

как интергармоники. При решении задач необходимо учитывать

все квазигармоники, а не только с частотами, кратными 50 Гц. В

противном случает оценка ЭМС будет существенно занижена –

тем больше, чем больше т отличается от единицы

Если отношение

не будет целым числом, то квазигармоники с

частотами µп отсутствуют, а оценивание ЭМС только по канониче-

ским гармоникам приведет к неверному выводу об отсутствии несину-

соидальности.