Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

122 Раздел 4

Среднее значение тока одного электроприемника получа-

ется умножением I на коэффициент включения, а дисперсия – I

на k

(1 – k

). Средние значения проекций токов суммируются. С

учетом (4.8) запишем выражение для суммарных средних значе-

ний (черта в обозначениях) проекций на ось х токов прямой по-

следовательности фазы А:

1 ввв

111

sin sin sin ,

BC CA

xA rr r rr r rr r

rrr

I kIkIkI

===

⎡

⎤

=ϕ+ϕ+ϕ

⎢

⎥

⎣

⎦

∑∑∑

где п

АВ,BC,СА

– количество электроприемников, подключенных

между соответствующими фазами.

Выражение для суммарных средних значений

1yA

анало-

гично – только вместо

sin

надо записать

cos .

Так как сла-

гаемые в этих выражениях однотипны, их можно объединить:

1 в 1 в

sin , cos .

ArrryArr

IkIIkI

ΣΣ

=ϕ=

∑∑

ϕ (4.19)

Точно так же определим суммарные проекции дисперсий

токов прямой последовательности:

()

1 вв

1sin

1cos

Arrr

yA r r r r

DI k k I

−ϕ

∑

(4.20)

Модуль среднего значения суммарного тока прямой по-

следовательности

111AxAy

III

(4.21)

и дисперсия

Методы расчета показателей ЭМС по несимметрии напряжений 123

()

11 1 вв

AxAyA rr

DI DI DI k k I

ΣΣΣ

=+= −

∑

(4.22)

не зависят от распределения электроприемников между фазами.

Иначе обстоит дело с обратной последовательностью. С

учетом табл. 4.1 суммарные средние значения проекций содер-

жат разнотипные слагаемые:

()

2 вв

sin 60 sin

sin 60 ,

cos 60 cos

cos 60 ,

BС

СA

BС

СA

xA r r r r r r

rr r

yA r r r r r r

rr r

IkI kI

⎡

=− °−ϕ− ϕ

⎢

⎣

⎤

+°+ϕ

⎥

⎦

⎡

=°−ϕ−

⎢

⎣

⎤

+°+ϕ

⎥

⎦

∑∑

∑

∑∑

∑

ϕ+

(4.23)

поэтому суммы нельзя объединять, а среднее значение

222AxAy

III

(4.24)

существенно зависит от распределения электроприемников.

Напротив, дисперсия

2 A

суммарного тока обратной

последовательности свойством инвариантности обладает. В са-

мом деле, в выражения для дисперсий проекций тока

() ( )

() () ( )

2 вв

22 22

вв вв

1sin60

1sin 1sin60

BC CA

xA r r r r

rrr r rrr r

DI k k I

kkI kkI

⎡

=− °−ϕ+

⎢

⎣

⎤

+− ϕ+− °+ϕ

⎥

⎦

∑

∑∑

124 Раздел 4

() ( )

() () (

2 вв

22 22

вв вв

1 cos 60

1cos 1cos60

BC CA

yA r r r r

rrr r rrr r

DI k k I

kkI kkI

⎡

=− °−ϕ+

⎢

⎣

⎤

+− ϕ+− °+ϕ

)

⎥

⎦

∑

∑∑

входят разнотипные слагаемые. Однако дисперсия суммарного

тока

()

22 2 вв

AxAyA rr

DI DI DI k k I

ΣΣΣ

=+= −

∑

(4.25)

не зависит от распределения электроприемников, так как суммы

квадратов синусов и косинусов дают единицы. Выражения

(4.22) и (4.25) тождественно совпадают.

Инвариантность дисперсии позволяет минимизировать

несимметрию по среднему значению (4.24). Перераспределени-

ем электроприемников по фазам полностью устранить несим-

метрию невозможно, поскольку дисперсия всегда отлична от

нуля. Например, для электроприемников с одинаковыми пара-

метрами

режима формула (4.24) дает

()()

2 в

AABCABCAB

IkInnnnn

=+−+

− (4.26)

В этом частном случае равномерное распределение по фа-

зам дает нулевое среднее значение, но дисперсия

()

2 вв

Inkk

=−I

при

≠ 0 в нуль не обращается. В общем же случае при разных

параметрах режима равномерное распределение

(

AB BC

)

далеко не всегда обеспечивает минимум несимметрии.

Методы расчета показателей ЭМС по несимметрии напряжений 125

При небольшом количестве электроприемников (п ≤ 3)

дискретное вероятностное распределение суммы токов проек-

ций получается путем перебора комбинаций совпадения вклю-

ченных состояний разного количества электроприемников. Ве-

роятности этих комбинаций и функции распределения приведе-

ны в табл. 4.2 для модулей тока. Эти же распределения относят-

ся и к проекциям токов. Номера электроприемников обозначены

римскими цифрами. Принято соотношение

< I

III

Таблица 4.2 – Вероятностные распределения нагрузок

группы однофазных электроприемников

Ток Вероятность

Функция

распределения

(

)

(

)

0 вI вII

kk=− −

(

)

I вI вII

kk=−

(

)

II вI вII

kk=−

0III

+ I

I,II вI вII

(

)

(

)( )

0 вI вII вIII

11 1

kk k=− − −

(

)

(

)

I вI вII вIII

kk k=− −

(

)

(

)

II вII вI вIII

kk k=− −

0III

III

(

)

(

)

III вIII вI вII

kkk=−−

0 III

+

+ I

(

)

I,II вI вII вIII

kk k=−

0I,II

+

+ I

III

(

)

I,III вI вIII вII

kk k=−

0I,III

+

+ I

III

(

)

II,III вII вIII вI

kk k=−

0II,III

+

+ I

III

I,II,III вI вII вIII

kk k

При

п ≥ 4 вероятностное распределение близко к нор-

мальному, так как при суммировании случайных величин или

процессов происходит их нормализация.

Вероятностные распределения нагрузок и их параметры

не зависят от законов распределения длительностей включения

126 Раздел 4

и пауз отдельных электроприемников. Корреляционные же

функции токов и проекций полностью определяются этими рас-

пределениями – за исключением значений в нуле, равных дис-

персиям. Общие формулы для корреляционных функций инди-

видуальных нагрузок приведены в § 3.3

[44].

Между изменениями нагрузки одного электроприемника

существует очевидная связь: за возрастанием нагрузки от 0 до

в момент включения через некоторое время следует ее спад до

нуля. На суммарном графике эта связь ослабевает: за увеличе-

нием нагрузки, вызванным включением одного электроприем-

ника, может последовать дальнейшее ее увеличение при вклю-

чении другого электроприемника. При большом количестве

электроприемников эта связь исчезает, а поток включений и от-

ключений становится

простейшим. В этом случае корреляцион-

ную функцию можно считать экспоненциальной с параметром,

определяемым средними значениями

вс

коэффициентов вклю-

чения и

интенсивностей включения. Для суммарного тока об-

ратной последовательности

()

{

}

222

exp ,

IA A

BDI

ΣΣ

=−ατ (4.27)

где параметр

(

)

2 свс вс

1kk,

=λ ⎡ − ⎤

⎣

⎦

(4.28)

а дисперсия вычисляется согласно (4.25):

()

2 вс вс

DI k k I

=−

∑

(4.29)

Характеристики нормального распределения тока обрат-

ной последовательности определяются формулами (4.29), а так-

же (4.23) и (4.24), в которых среднее значение коэффициентов

включения выносится за знак сумм.

Методы расчета показателей ЭМС по несимметрии напряжений 127

4.3. Расчет показателей ЭМС в рамках статических моделей

Статические модели ЭМС используются либо при неиз-

менной несимметрии либо для безынерционных объектов (п.

3.2). В первом случае расчет показателей ЭМС не вызывает

трудностей. Во втором случае затруднения также не возникают,

если помеха задана графиком изменения коэффициентов не-

симметрии: этот график возводится в квадрат и умножается на

соответствующие коэффициенты

2ϑ

и с

2∆Р

. Затем по получен-

ному графику температуры вычисляются средняя температура и

расчетное максимальное значение (с граничной вероятностью

0,05), а по графику потерь мощности – их среднее значение.

Если исходная информация задана в виде теоретического

вероятностного распределения коэффициентов несимметрии, то

по формулам (2.39), (2.40) и табл. 2.1 может быть получено ве-

роятностное распределение квадратов коэффициентов несим-

метрии

, а с учетом (2.34) – распределение температур и потерь

мощности. Если задана статистическая функция распределения,

то функция распределения квадратов коэффициентов несиммет-

рии получается нелинейным преобразованием оси абсцисс, ис-

ходя из условия

(

)

(

)

FK FK=

(4.30)

Проиллюстрируем это на примере статистической функ-

ции распределения коэффициентов несимметрии, которая пред-

ставлена на рис. 4.3 кривой 1 и воспроизведена на рис. 4.4 слева.

Согласно (4.30) ордината точки

а для значения коэффициента

несимметрии 2 % совпадает с ординатой точки

b квадрата этого

коэффициента, равного 4 (%)

. Выполнив такие преобразования

для всех значений абсцисс исходного графика, получим иско-

мую функцию распределения, показанную на рис. 4.4 справа.

Однако для рассматриваемых показателей ЭМС опреде-

лять вероятностные характеристики квадратов коэффициентов

несимметрии не вызывается необходимостью. Во-первых, из

соотношения (4.30) следует, что взятое с граничной вероятно-

стью 0,05 расчетное максимальное значение квадратов коэффи-

128 Раздел 4

циентов несимметрии равно квадрату расчетного значения

. Поэтому расчетный максимум температуры

2maxU

(4.31)

2max 2 2 max

∆ϑ =

0,2

0,4

0,6

0,8

0123

0,2

0,4

0,6

0,8

048

% (%)

Рис. 4.4. Построение функции распределения квадратов

коэффициентов несимметрии

Во-вторых, среднее значение температуры, для которого

соотношение вида (4.31) не корректно, сразу вычисляется по

квадрату эффективного значения

2Uэ

коэффициента несиммет-

рии:

с 22э 22с 2

cK c K

ϑϑ

∆

ϑ= = +σ

(4.32)

Аналогично находится среднее значение потерь мощности

с 22э 22с 2

PU P U K

PcK c K

∆∆

∆

== +σ

(4.33)

Для графика на рис. 4.1,г расчетное значение

2maxU

2,26 %, а

в то время как

()

222

2 э

1, 0 43 0, 583 1, 428 % ,

K =+ =

Методы расчета показателей ЭМС по несимметрии напряжений 129

()

2 с

1, 043 1, 08 8 % .

K == Поэтому, если бы средняя темпера-

тура рассчитывалась по формуле вида (4.31), то ошибка соста-

вила бы –23,8 %.

4.4. Расчет кумулятивных коэффициентов несимметрии

по графику помехи

Приведенные кумулятивные коэффициенты несимметрии

напряжений

2w[θ]

длительностью [θ] = 3 с (п. 3.8) рассчитыва-

ются для проверки выполнения норм стандарта

[6]. Расчет не

требуется лишь в двух случаях. Во-первых, если наибольшее

значение

2UM

не превышает 2 %, требования стандарта заведо-

мо выполняются. Во-вторых, поскольку трехсекундный кумуля-

тивный максимум не может быть больше эффективного значе-

ния коэффициента несимметрии, то при

[

]

2 э 2н

KK>=

требования стандарта безусловно нарушаются.

Перед расчетом по заданному графику коэффициентов не-

симметрии целесообразно проверить выполнение условия (1.22),

которое в решаемой задаче принимает вид

2 с 2 эд

1 100.

−

≤δ

(4.34)

Если оно не нарушается, то вместо квадратичного кумуля-

тивного осреднения достаточно выполнить трехсекундное ос-

реднение исходного графика, а не его квадрата. Например, для

графика на рис. 4.1,г требуется квадратичное трехсекундное ос-

реднение, так как

2UM

= 3,17 > 2 %, K

2Uэ

= 1,195 < 2, а величина

1 1,043 1,195 0,127 0,1.−=>

Осреднение выполняется в следующей последовательно-

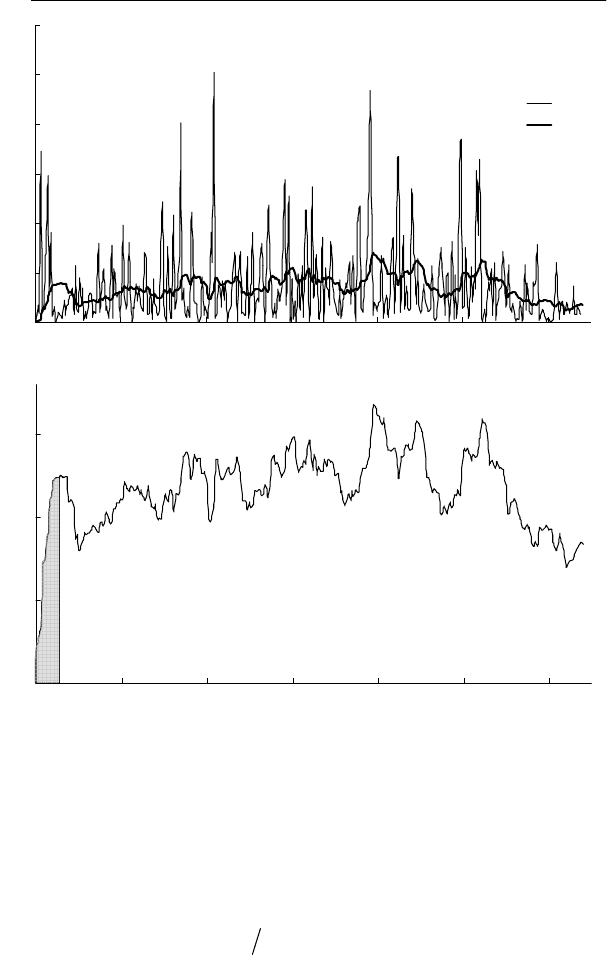
сти. Исходный график возводится в квадрат (рис. 4.5, кривая 1).

Согласно (1.25) при

t = 0 интервал осреднения располагается

слева от оси ординат, не захватывая график. Поэтому осреднен-

130 Раздел 4

0 102030405060

0,5

1,5

0 102030405060

2w[θ]

(%)

2[θ]

, c

[θ]

Рис. 4.5. К определению трехсекундного кумулятивного

графика коэффициентов несимметрии напряжений при работе

ДСП-100

ное на интервале значение равно нулю – оно относится к концу

интервала, т.е. к

t = 0. Затем интервал осреднения сдвигается на

шаг

∆ вправо, захватывая начальную ординату

(

)

Усред-

ненное значение

(

)

[

]

∆

⋅θ

относится к моменту t = ∆. Ин-

Методы расчета показателей ЭМС по несимметрии напряжений 131

тервал снова сдвигается на шаг ∆, и т.д. Полученный энергети-

ческий кумулятивный процесс

2[θ]

(t) представлен на рис. 4.5

кривой 2. Извлекая из ординат этого графика квадратный ко-

рень, получим искомый процесс (кривая 3).

На начальном участке протекает случайный переходный

процесс. Из рис. 1.6 (ломаная 1) следует, что этот процесс пол-

ностью заканчивается ровно через 3 с. Отбросив участок графи-

ка от 0 до 3 с (затушеванная область), получим график стацио-

нарного режима.

Для него вычислим эффективное значение

2[θ]э

= 1,203 % и стандарт σ

2[θ]

= 0,201 %, а также построим

функцию распределения

F(K

2w[θ]

), представленную на рис. 4.6

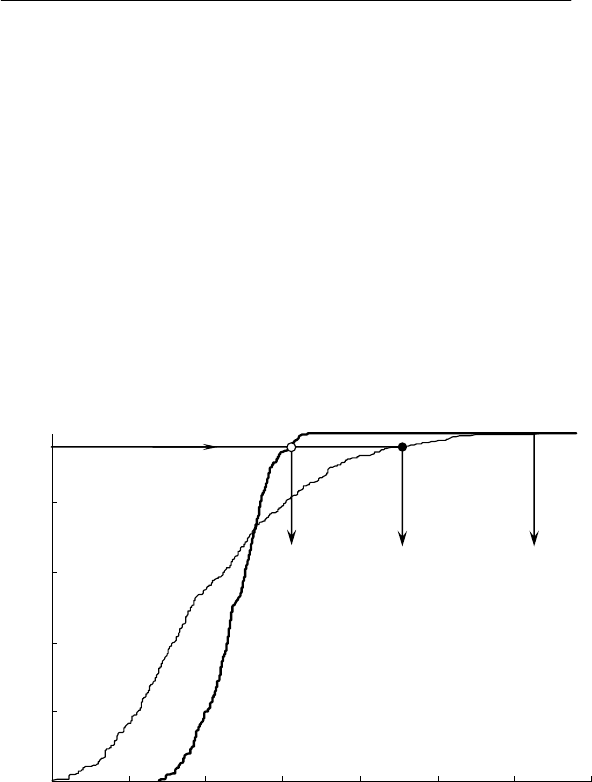
кривой 1. Здесь же для сравнения показана функция распреде-

ления исходного графика (кривая 2). Так как осреднение сгла-

живает график, то кривая 1 менее пологая, чем кривая 2.

0,2

0,4

0,6

0,8

00,511,522,533,5

2[θ]н max

0,95

2θ

2w[θ]

2Umax

2UM

Рис. 4.6. Функция распределения коэффициентов несим-

метрии напряжений при работе ДСП-100: 1 – трехсекундных, 2 –

исходных