Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

12 Раздел 1

Dx x x

−

(1.3)

или стандарт

.Dxσ=

Дисперсия характеризует отклонения

значений случайной величины от ее среднего значения, а квад-

рат эффективного значения – среднюю мощность процесса.

Вид закона распределения стремятся выбирать из физиче-

ских соображений. На форму графика помехи влияет большое

количество случайных факторов, что дает основание во многих

случаях использовать нормальный закон распределения ординат

помехи, который полностью

характеризуется средним значени-

ем и стандартом.

При

(

)

/xx

=− σ

плотность и закон нормального закона распределения записы-

ваются в виде

{}

() exp /2,

fx=−Π

() ( ),Fx

∗

ΦΠ

(1.4)

где

()

∗

– табулированная функция стандартного нормального

распределения с нулевым средним значением и единичным

стандартом [3, 50].

Абсциссы нормального распределения изменяются от ми-

нус до плюс бесконечности. Это может препятствовать его

практическому применению, если расчетные значения ординат

помехи выходят за пределы диапазона (х

, х

) их возможных

значений. В этих случаях используются либо усеченное нор-

мальное распределение [54], либо распределения в пределах

диапазона изменения случайной величины. Одним из них явля-

ется равномерное распределение с плотностью

Построение моделей электромагнитной совместимости 13

f(x) = 1

κ,

постоянной в диапазоне κ = х

– х

и равной нулю за пределами

диапазона.

Соответствующая функция распределения

(

()

)

xxx=−

(1.5)

определяется в том же диапазоне. При х < x

она равна нулю, а

при х ≥ x

– единице.

Равномерное распределение, как и нормальное, определя-

ется средним значением и стандартом

(

)

смМ

/2, /2 3,xxx=+ σ=κ

через которые можно выразить предельные значения

М,мс

3.xx

±σ

Постоянство плотности распределения существенно уп-

рощает выкладки, в связи с чем этот закон распределения целе-

сообразно использовать хотя бы для первого приближения. На-

пример, он был принят в методе упорядоченных диаграмм [17].

Перейдем к динамическим моделям (п.1.2), когда нельзя

пренебрегать переходными процессами. В связи с этим понятие

случайной

величины недостаточно для определения характери-

стики реакции, а требуется использовать понятие случайного

процесса.

У нестационарных случайных помех характеристики за-

висят от времени и определяются для каждого момента времени

по большому количеству записей помехи (ансамблю реализа-

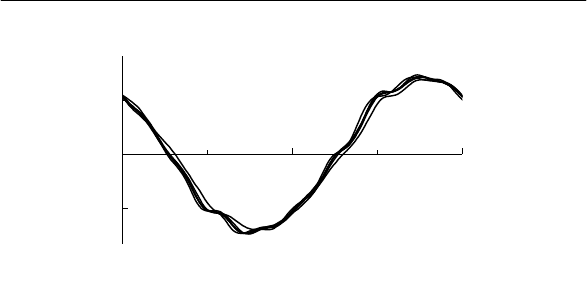
ций). Для примера на рис. 1.2 показана часть графиков напряже-

ния и на шинах 6 кВ подстанции, питающей

дуговую сталепла-

вильную печь (ДСП).

14 Раздел 1

-200

-100

100

200

0 0,01 0,02

% и

Рис. 1.2. Часть ансамблей реализаций мгновенных значе-

ний напряжения на шинах 6 кВ

В практических приложениях нестационарные процессы

разбиваются на участки стационарности, в пределах которых

характеристики стационарных помех от времени не зависят. Ес-

ли связь между отдельными ординатами с увеличением дли-

тельности τ между ними ослабевает, а при τ → ∞

исчезает, то

характеристики такого эргодического стационарного процесса

можно определять не по ансамблю реализаций, а по одной реа-

лизации большой длительности Т

(теоретически Т

→ ∞).

Так как нарушающий ЭМС электроприемник может

включиться в любой заранее неизвестный момент времени, то

даже при строго периодической работе электроприемника поме-

ху рассматривают как стационарный случайный процесс с пе-

риодическими реализациями. Все реализации такого процесса

одинаковы, но сдвинуты друг относительно друга случайным

образом. Этот стационарный процесс не является

эргодическим,

однако его характеристики можно определять по одной реали-

зации, но только за время t

длительности цикла или кратное ей.

В каждый момент времени совокупность ординат ансамб-

ля реализаций представляет собой случайную величину со сво-

им законом распределения. Степень линейной связи (корреля-

ции) между моментами времени, разделенными интервалом τ,

характеризует корреляционная функция (КФ)

(

)

,Ktt

с аргу-

Построение моделей электромагнитной совместимости 15

ментом τ. У стационарных процессов законы распределения и

КФ K

(τ) не зависят от времени. Для нормальных процессов не-

коррелированность означает независимость ординат, а у процес-

сов с другими законами распределения отсутствие корреляции

еще не означает независимость.

КФ используется при анализе изменения процессов во

времени. При частотном анализе стационарные процессы харак-

теризуются спектральной плотностью S

(ω), где ω ≥ 0 – угловая

частота. Понятие мгновенной спектральной плотности можно

формально ввести и для нестационарного процесса, но оно не

имеет наглядного физического смысла.

Спектральная плотность и КФ связаны прямым и обрат-

ным косинус-преобразованиями Фурье [3]:

() ()cos , () ()cos ,SKdKS

∞∞

ω= τ ωττ τ= ω ωτω

∫∫

(1.6)

которые часто записываются с разными нормированными мно-

жителями: например, в [50] множитель 2

π стоит перед КФ.

Удобство (1.6) состоит в том, что интеграл от спектральной

плотности равен дисперсии:

(0) ( ) .DKSd

∞

σ= = ω ω

∫

(1.7)

C увеличением длительности между ординатами корреля-

ционная связь затухает: монотонно (при отсутствии почти пе-

риодической составляющей) или с колебаниями. В первом слу-

чае КФ обычно аппроксимируется недифференцируемым выра-

жением

{

}

() exp ,K

=σ −ατ (1.8)

а во втором – недифференцируемым или дифференцируемым

выражениями

16 Раздел 1

{

}

() exp cos ,K

=σ −ατ ωτ (1.9)

{

}

( ) exp (cos sin ),K

∗

=σ −ατ ωτ+α ω τ (1.10)

где α и ω

– параметры,

∗

=α ω

Экспоненциальная КФ (1.8)

является частным случаем (1.9) при ω

= 0.

Для упрощения выкладок КФ (1.9) и (1.10) удобно пред-

ставить в виде суммы экспонент с мнимыми показателями сте-

пени, используя известные соотношения:

{}{}

()

{}{}

()

cos exp exp ,

sin exp exp

τ= ωτ+ −ωτ

τ= −ω τ − ω τ

(1.11)

при

1.j =−

Нормированная КФ

(

)

(

)

/.RK

=τσ

Корреляционным функциям (1.8)-(1.10) соответствуют

спектральные плотности

()

ω=σ

πα +ω

(1.12)

()

() ()

21 1

⎡

⎤

ω=σ +

⎢

⎥

α+ω+ω α+ω−ω

⎣

⎦

(1.13)

()

() ()

∗

ω+ω ω−ω

⎡

⎤

ω=σ +

⎢

⎥

α+ω+ω α+ω−ω

⎣

⎦

(1.14)

Построение моделей электромагнитной совместимости 17

При наличии нескольких апериодических и периодиче-

ских составляющих используется линейная комбинация рас-

смотренных выражений для КФ.

О степени затухания корреляционных связей судят по

времени корреляции

() .

∞

=τ

∫

τ (1.15)

Экспоненциальная КФ (1.8) имеет

= 1

α.

Интегралы (1.15) от выражений (1.9) и (1.10) представля-

ются в виде суммы бесконечного числа интегралов, которые об-

разуют геометрические прогрессии. Знаменатели и суммы про-

грессий определяются без затруднений. В результате при

получим следующие формулы для времен корреля-

ции КФ вида (1.9) и (1.10):

∗

ϕ=πα

()

{}

()

csch ,

1 exp csch

∗

=α+

α+α

+ϕ ϕ

τ=

α+α

Теоретической абстракцией является белый шум ζ(

t), ко-

торый имеет постоянную спектральную плотность

с, бесконеч-

ную дисперсию и КФ

(

)

(

)

,Kc

=π δ τ (1.16)

выражаемую через дельта-функцию δ(

t). У белого шума корре-

ляция между ординатами отсутствует.

18 Раздел 1

Методологически важно, что стационарные случайные

процессы возникают в результате преобразования белого шума

некоторой гипотетической линейной системой, не всегда явно

выраженной. Так, процесс с экспоненциальной КФ получается

преобразованием белого шума апериодическим (инерционным)

звеном первого порядка, с КФ (1.9) – колебательным и форси-

рующим звеньями, с КФ (1.10) – колебательным звеном.

Замена реальных процессов белым шумом упрощает

вы-

кладки. Это возможно, если время корреляции намного меньше

постоянной времени инерции рассматриваемого объекта, что

равносильно быстрому затуханию амплитудно-частотной функ-

ции (АЧФ) объекта по сравнению со спектральной плотностью.

В этом случае в расчетном диапазоне частот спектральная плот-

ность практически постоянна с параметром

(0) 2 / .cS

≈

=στ π

(1.17)

Помехи обычно измеряются в процентах или о.е. по от-

ношению к номинальным параметрам режима.

Коррелированность ординат двух случайных процессов

x(t) и y(t) характеризуется взаимной КФ K

(τ), а в совпадающие

моменты времени (τ = 0) – моментом

взаимной корреляции.

Нормированная взаимная КФ и коэффициент взаимной корре-

ляции определяются формулами

() ()/ , / ,

yxyxyxyxyx

RK RK

=τσσ = σσ

где σ

и σ

– стандарты процессов. Физически наличие взаимной

корреляции свидетельствует об энергетическом взаимодействии

между процессами.

Вопрос о коррелированности между помехами решается

на основе физических соображений (независимость выполняе-

мых электроприемниками технологических операций и др.). Де-

ло в том, что взаимные КФ теоретически должны определяться

по реализации бесконечной длительности или – для неэргодиче-

ских процессов – по

ансамблю бесконечного числа реализаций.

На практике длительность записи и количество реализаций ог-

Построение моделей электромагнитной совместимости 19

раничены, поэтому между попарно взятыми реализациями неза-

висимых процессов взаимная КФ может не обращаться в нуль,

особенно при наличии периодических составляющих. В [54] это

явление названо псевдокорреляцией.

Характерным примером являются два независимых пе-

риодических процесса

х(t) и у(t), имеющие одинаковые реализа-

ции. Каждый из них представляет собой стационарный неэрго-

дический процесс (п.1.3), а их средние значения, дисперсии и

КФ

k(τ) могут быть определены по одной реализации за время

цикла

. Однако для вычисления взаимного корреляционного

момента уже нельзя ограничиться двумя реализациями каждого

из процессов. Эти реализации имеют случайный сдвиг η во вре-

мени, равномерно распределенный в пределах

. Для них вза-

имный псевдокорреляционный момент «по реализациям» равен

значению КФ при τ = η:

ηху

= k(η).

Обработка же «по ансамблю» предполагает перебор всех

бесконечно возможных значений сдвига, что равносильно ос-

реднению псевдокорреляционного момента по η. Для независи-

мых периодических процессов такое осреднение дает верный

результат:

ху

= 0.

Если длительности циклов различны, но соизмеримы, то

псевдокорреляционный момент вычисляется за время, равное

наименьшему общему кратному длительностей циклов. Если

длительности циклов несоизмеримы, то псевдокорреляция от-

сутствует – но только при реализациях бесконечной длительно-

сти.

В качестве иллюстрации на рис. 1.3 показаны графики

суммы

u(t) двух периодических процессов с прямоугольными

импульсами, длительность которых равна длительности паузы с

разными сдвигами: а – промежуточное значение случайного

сдвига, б – при нулевом сдвиге и в – при η =

2. Графики сум-

мы имеют ту же длительность цикла, но их форма зависит от

величины сдвига.

Поскольку процессы независимы, то дисперсия суммы

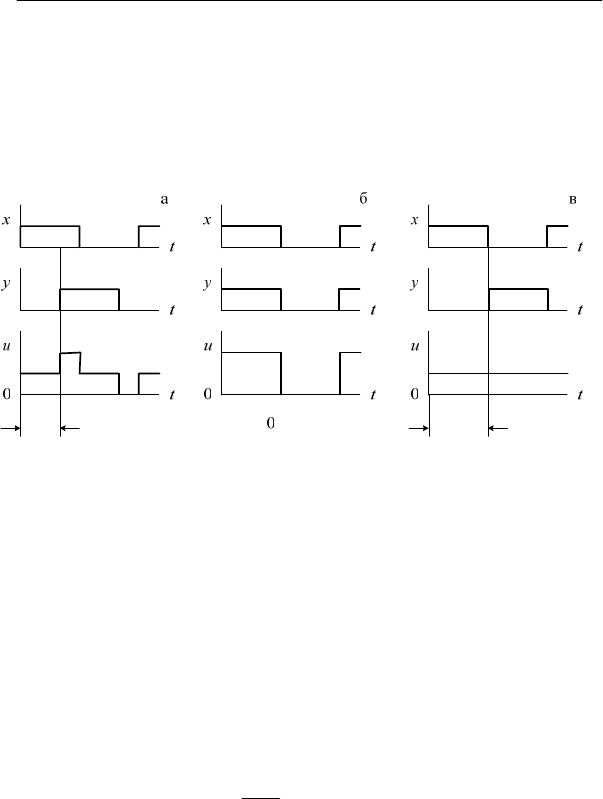
20 Раздел 1

uDxDy Dx

Вместе с тем, псевдодисперсии суммы различны и изме-

няются от 4

Dx при нулевом сдвиге до 0 при η = t

2. Осредне-

ние псевдодисперсий по величине сдвига дает правильный ре-

зультат.

Рис. 1.3. Суммирование периодических процессов

1.4. Моделирование инерционности

Модели ЭМС должны отражать основные свойства объек-

тов, но быть предельно простыми. Инерционность объекта часто

достаточно моделировать инерционным звеном первого поряд-

ка, постоянная времени

Т которого совпадает с постоянной

инерции объекта. В этом случае процессы на входе и выходе

блока КСИ (рис. 1.1) связаны дифференциальным уравнением

+=y

(1.18)

Обозначив через

оператор инерционного сглаживания,

запишем (1.18) в компактном виде

{

}

() ().

wt L yt= (1.19)

Построение моделей электромагнитной совместимости 21

Квадратичный инерционный процесс имеет размер-

ность квадрата реакции. В связи с этим удобно использовать

приведенный инерционный процесс

()

() (),

wT T

yt wt=

(1.20)

размерность ординат которого совпадает с размерностью орди-

нат реакции.

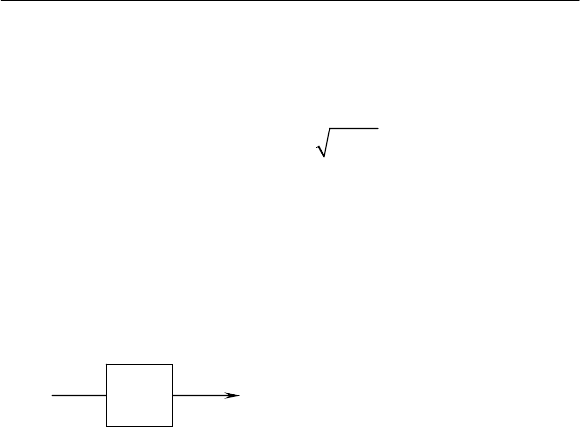
При малых различиях в эффективном

и среднем у

зна-

чениях реакции блок КСИ может быть линеаризован. В этом

случае квадратор исключается, а остается лишь инерционное

у у

Рис. 1.4.

звено (рис. 1.4). Инерционный

процесс на выходе звена

{

}

() ().

yt L yt=

(1.21)

Найдем условие, при ко-

тором с заданной относитель-

ной погрешностью δ

, выра -

женной в процентах, возможна линеаризация. Максимальные

значения процессов (1.20) и (1.21) монотонно убывают с увели-

чением постоянной инерции. При

Т = 0 они совпадают, а при

неограниченном увеличении постоянной инерции максимум

приведенного инерционного процесса равен эффективному зна-

чению, а инерционного – среднему. В этом предельном случае

достигается наибольшее расхождение между максимумами. От-

сюда следует условие применимости преобразования (1.21):

(

– у

)

≤ δ

100

или

1 – 1

≤ δ

100, (1.22)

где

= у

– коэффициент формы. Для принятой в теории

электрических нагрузок

[52] десятипроцентной допустимой по-