Кузьмин Д.В. Моделирование динамики мехатронных систем. Уравнения и алгоритмы
Подождите немного. Документ загружается.

Решение
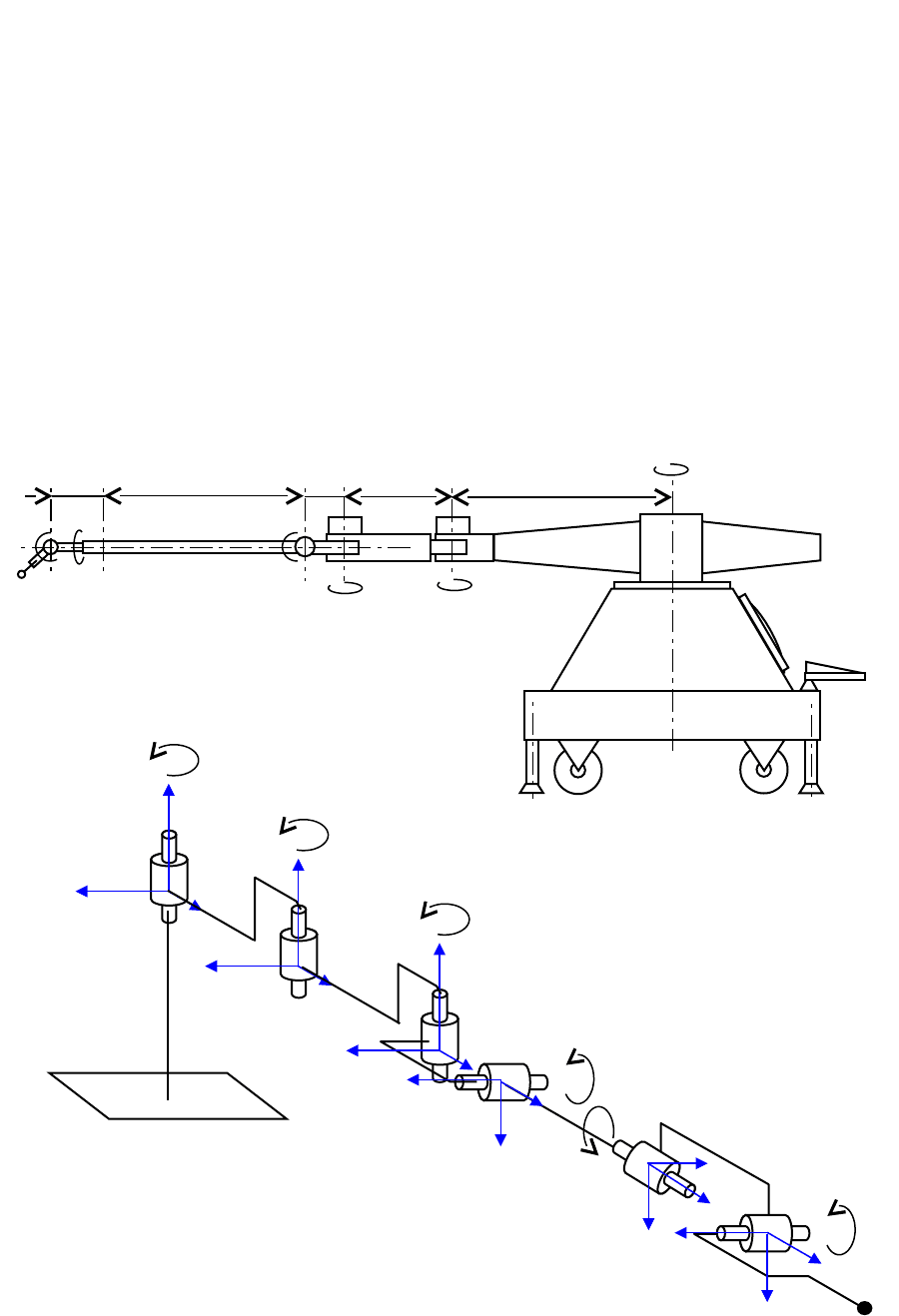
Геометрическая модель механизма КИМ в положении
0q
,
выполненная в CAD-системе с использованием принятых графических
изображений шарниров, показана на рис. 3.19; расстояния между осями
шарниров условно не показаны. Пусть отрезки, изображающие векторы
iii
kji ,,
,
6,,1 i
, имеют длину 1 мм. Тогда матрицы абсолютных
координат крайних точек этих отрезков будут следующими:
000000
460044652595250017000
000000
O
,
111000
460044652595250017000
000111
I
,
000000
460144652596250117011
010000
J
,
000111
460044662595250017000
101000
K
.
71
1870
1700
800
95
q
1
q
2
q
3
q
4
q
5
q
6
Рис. 3.18
q
5
q
3
q
4
q
6
x
3
z
3
y
3
y
4
z
4
x
4
z
5
y
5
x
5
z
6
y
6
x
6
O
5
O
4
q
2
x
2
z
2
y
2
q
1
y
0
, y
1
С
6
x
0
, x
1
z
0
, z
1
O
3
O
2
O
0
, O
1
Рис. 3.19
1
2
1
2

Матрицы, задающие преобразования координат, связанные с
перемещением звеньев в кинематических парах, описываются формулами
(3. 46):
1000
0100
00
00
ii
ii
i
CS
SC
Q
, где
ii
qC cos
,
ii
qS sin
,
6,,1 i
.
Матрицы O, I, J, K, Q являются исходными данными расчетной
программы, написанной на алгоритмическом языке системы Mathcad и
реализующей алгоритм (рис. 3.17). Расчетная программа и результат ее
выполнения – аналитическая запись вектора абсолютного положения
точки C
6
в базовой системе координат
0000
zyxO
приведены в приложении
1.
3.8. Алгоритмы формирования уравнений динамики
системы с сосредоточенными массами
Дадим алгоритм формирования уравнений динамики (3.4) для
системы без ветвления с точечными массами [21, 24]. Проекции скоростей
центров масс звеньев на оси неподвижной системы координат
0000
,,, zyxO
вычислим по формулам
i
j
j
j
i
i
q
q
u
x
1
1
0
,
i
j
j
j
i
i
q
q
u
y
1
2
0
,
i
j
j
j
i
i
q
q
u
z
1
3
0
, где
72
1
2
1
2
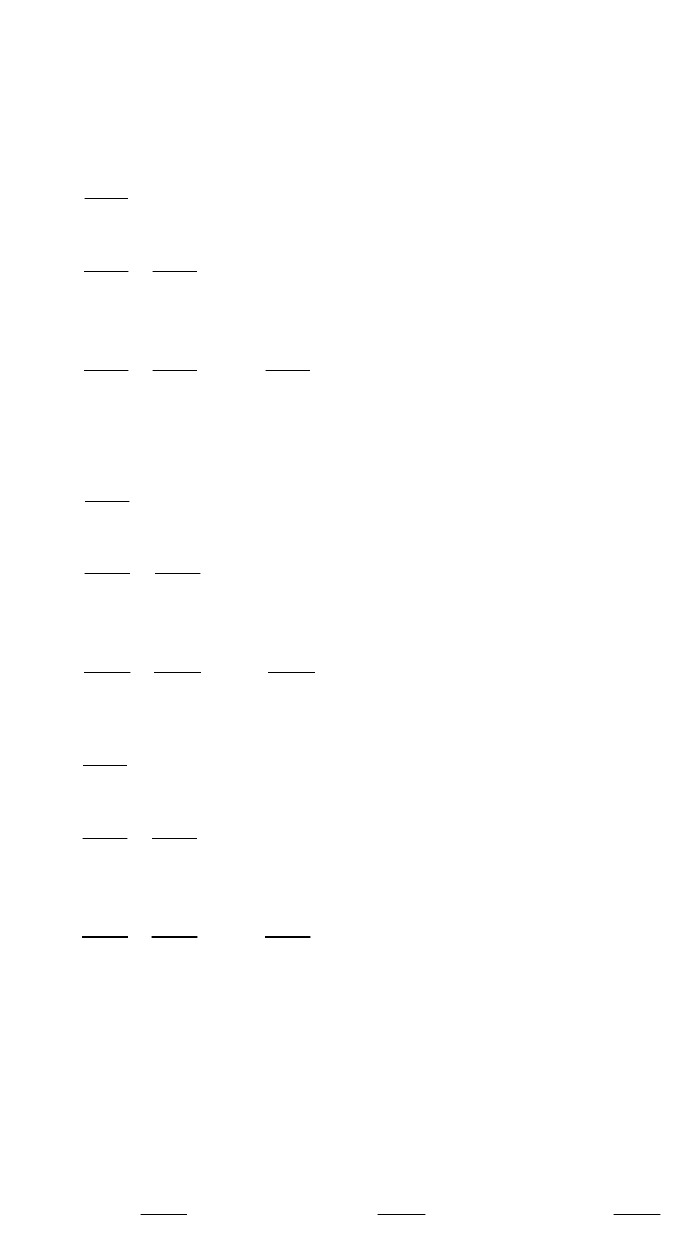
),,(
11
0
iiCi
qqux
,
),,(
12
0
iiCi
qquy
,
),,(
13
0
iiCi
qquz
- абсолютные
координаты центров масс звеньев. Собирая одноименные проекции
абсолютных скоростей центров масс в матрицы-столбцы, будем иметь:
n
n
nnn
n
q
q
q
q
u
q
u
q
u
q
u
q
u
q
u
x
x
x
2
1
1
2
1
1
1
2
12
1
12
1
11
0
0
2
0
1
00
000
,
,
1
qUx
(3.53)
n
n
nnn
n
q
q
q
q
u
q
u
q
u
q
u
q
u
q
u
y
y
y
2
1
2
2
2
1
2
2
22
1
22
1
21
0
0
2
0
1
00
000
,
qUy
2
, (3.54)
n
n
nnn
n
q
q
q
q
u
q
u
q
u
q
u
q
u
q
u
z
z
z
2
1
3
2
3
1
3
2
32
1
32
1
31
0
0
2
0
1
00
000
,
qUz
3
. (3.55)
В формулах (3.53) – (3.55) верхний индекс «0» обозначает проекции
скоростей на оси неподвижной системы координат. Соответственно, для
абсолютных ускорений центров масс звеньев получим уравнения
i
n
i
i
qq
q
U
qUx
1
1
1
,
i
n
i
i
qq
q
U
qUy
1
2
2
,
i
n
i
i
qq
q
U
qUz
1
3
3
. (3.56)
Уравнения динамики системы будут иметь вид
73
1
2
1
2
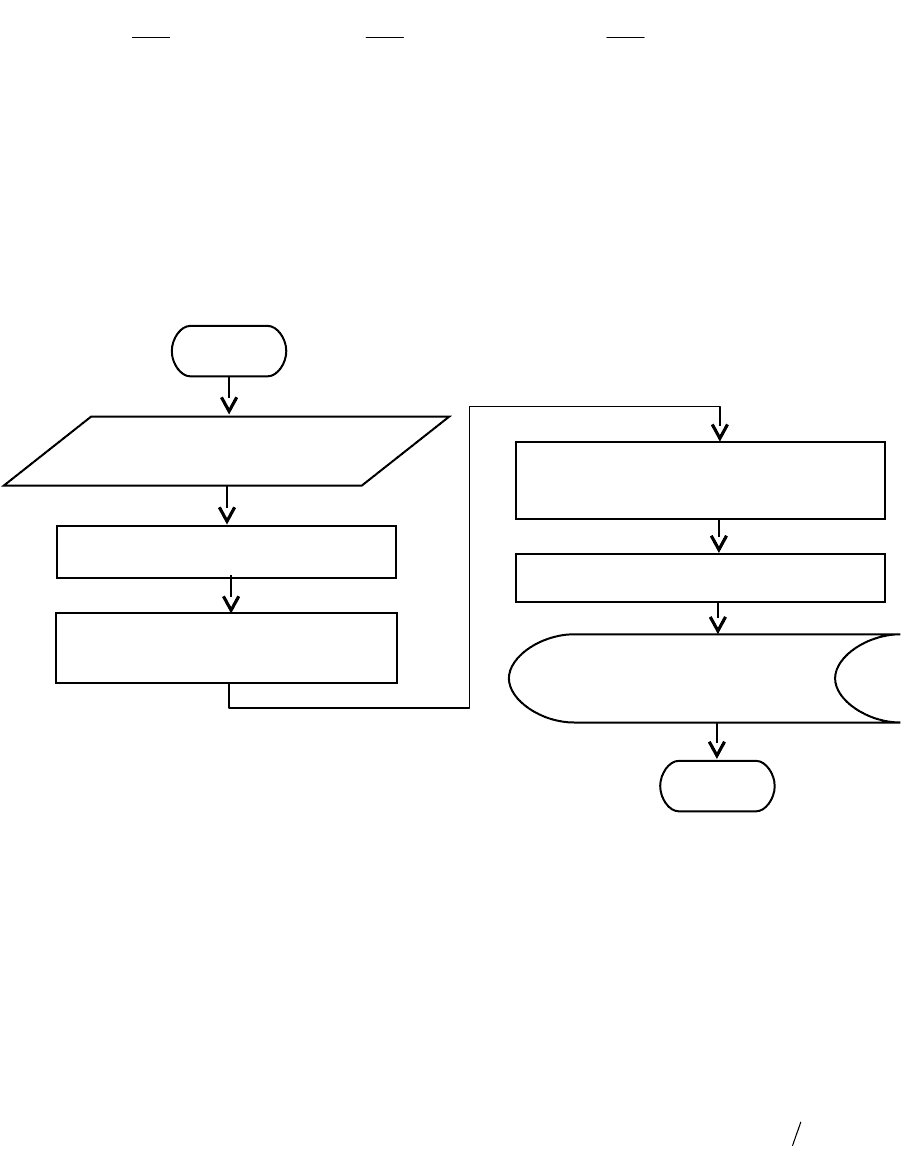
,,,2,1
,)()()()(
1
33
0
0
22
0
0
11
0
0
mj
Fgzm
q
z
Fgym
q
y
Fgxm
q
x
tQ
n
i
iii
j
i
iii
j
i
iii
j
i
j
(3.57)
где
T
iiii
FFFF
321
- равнодействующие сил внешней нагрузки,
T
gggg
321
- ускорение свободного падения.
Алгоритм, формирующий уравнения динамики согласно (3.56), (3.57)
приведен на рис. 3.20. Данный алгоритм эффективен, когда число степеней
свободы разомкнутой цепи с вращательными кинематическими парами
4m
.
На разомкнутый механизм с вращательными соединениями в
процессе движения кроме n компонент сил инерции звеньев,
обусловленных обобщенными ускорениями, действует
)1(21
1
nnj
n
j
компонент сил инерции, обусловленных обобщенными скоростями.
Например, выражения для проекций абсолютного ускорения центра
масс последнего звена в случае механизма с шестью вращательными
74
5. Запись уравнений
динамики в файл
3. Формирование выражений для абсолютных
ускорений
r
i
(q
1
,…,q
i
), m
i
, F
i
, g, i=1,…,n
1. Формирование матриц U
1
, U
2
, U
3
2. Вычисление ∂U
k
/∂q
i
, k = 1,2,3,
i = 1,…n
4. Формирование уравнений динамики
начало
конец
Рис. 3.20
1
2
1
2

парами будут содержать
27
компонент, зависящих от скоростей и
ускорений. Суммирование этих проекций согласно (3.57) приводит к
громоздкому аналитическому выражению, для упрощения которого
потребуется большой объем оперативной памяти. Решение проблемы
может быть осуществлено двумя способами:
1) увеличением объема оперативной памяти компьютера;
2) модификацией вычислительного алгоритма.
Первый способ малопригоден, так как, при повышении числа
степеней свободы, оперативной памяти компьютера может оказаться
недостаточно. Поэтому наиболее рациональным будет второй способ,
состоящий в изменении алгоритма (рис. 3.20) таким образом, чтобы
выражения для компонент сил и моментов вычислялись и упрощались по
отдельности. В этом случае при выполнении процедуры упрощения
отпадает необходимость загружать выражение для управляющей силы или
момента целиком в оперативную память компьютера.
Обратимся к выражениям (3.56) описывающим проекции ускорений
центров масс звеньев на оси неподвижной системы координат. Так как
уравнения связей получаются путем ортогональных преобразований, то
сомножители при компонентах проекций ускорений представляют собой
функции, содержащие синусы и косинусы обобщенных координат.
Следовательно, при вычислении сил и моментов сил инерции,
действующих по обобщенным координатам, сомножители при одинаковых
инерционных компонентах должны сокращаться (образуя
тригонометрические единицы или взаимно уничтожаясь). Это означает,
что, складывая по отдельности проекции одноименных компонент сил
инерции на оси неподвижной системы координат, а затем, суммируя
полученные простые слагаемые, можно формировать уравнения динамики
без необходимости упрощать громоздкие аналитические выражения.
Поясним изложенный способ на простом примере. Пусть требуется
получить уравнение динамики системы (рис. 3.21), состоящей из
невесомого стержня длины L, шарнирно прикрепленного к неподвижному
75
1
2
1
2
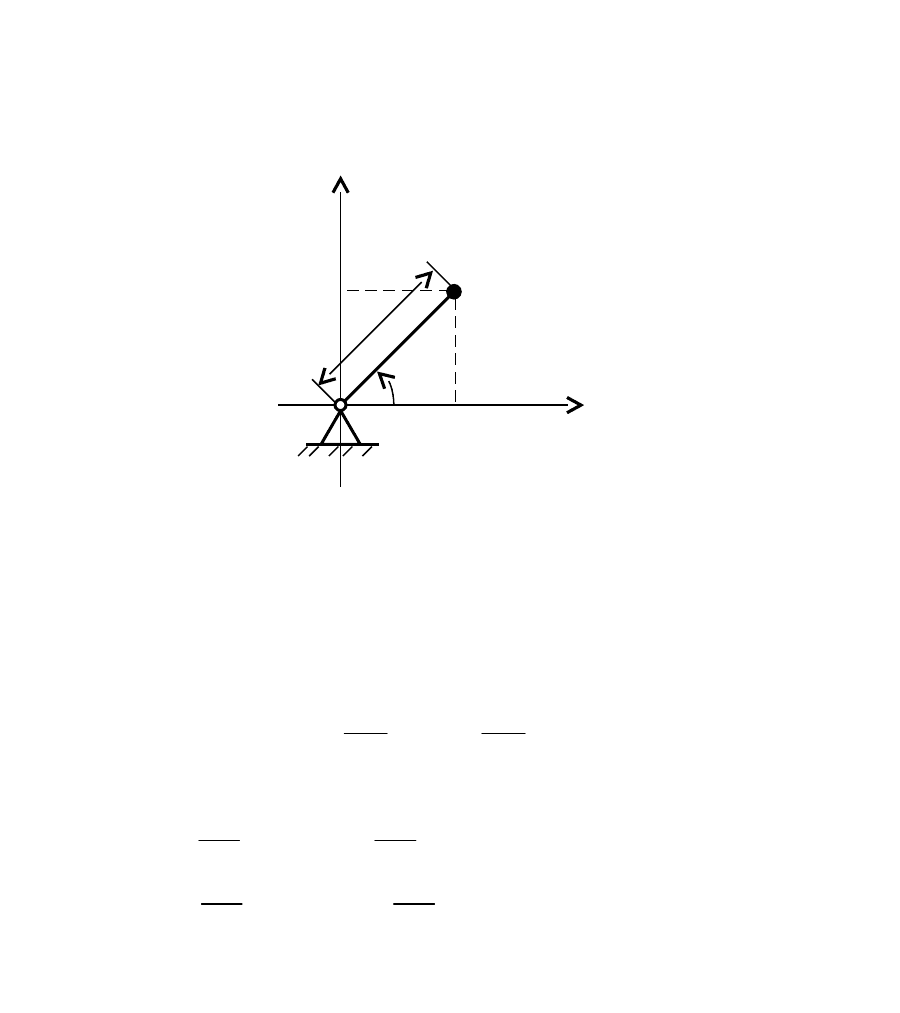
основанию одним концом и массой m, помещенной в точке C, на другом
конце.
Уравнения, описывающие положение точки C имеют вид:
., LSqyLCqx
CC
Проекции абсолютного ускорения точки C будут
выражаться следующими зависимостями:
.,
22
SqqLCqqLyCqqLSqqLx
CC
Число степеней свободы системы n = 1. Проекции ускорения точки C
содержат две компоненты, одна из которых зависит от
q
, а другая – от
q
.
Частные производные, определяющие функциональные преобразователи
связного графа, равны:
., LCq
q
y
LSq
q
x
CC
Уравнение динамики
системы имеет вид:
)()(
21
qMqMM
,
.0)()()()(
,)()()()(
2222
2
2222
1
CqSqSqCqqmLSqqL
q
y
mCqqL
q
x
mqM
qmLqCqSqmLCqqL
q
y
mSqqL
q
x
mqM
CC
CC
Суммируя компоненты M
1
и M
2
, окончательно получаем:
qmLM
2
.
Усовершенствование алгоритма (рис. 3.20) будет заключаться лишь в
изменении порядка выполнения символьных операций, предусмотренных
уравнениями (3.56) и (3.57): упрощение уравнений динамики будет
вестись покомпонентно. Таким образом, уравнения динамики, получаемые
76
x
y
O
L
C, m
q, M
x
C
y
C
Рис. 3.21
1
2
1
2
при помощи нового алгоритма, не будут нуждаться в процедуре конечного
упрощения, требующей большого объема оперативной памяти.
Представим проекции ускорений точек системы (3.56) в следующем
виде:
xxx
~
,
yyy
~
,
zzz
~
, (3.58)
где
qUx
1
,
qUy
2
и
qUz
3
- компоненты, обусловленные
обобщенными ускорениями;
n
l
ll
qqx
1
1
~
,
n
l
ll
qqy
1
2
~
и
n
l
ll
qqz
1
3
~
-
компоненты, обусловленные обобщенными скоростями;
,
l
k
kl
q
U
3,2,1k
. С учетом (3.58) уравнение динамики (3.57) принимает вид [22,
24]:
KBFGSMQ
, (3.59)
где
T
n
QQQQ
21
- вектор управляющих сил и моментов,
T
n
MMMM
21
- вектор сил и моментов сил инерции,
обусловленных ускорениями в соединениях,
T
n
SSSS
21
- вектор
центробежных, кориолисовых сил и моментов сил инерции,
T
n
GGGG
21
- вектор сил и моментов сил тяжести,
T
n
FFFF
21
- вектор сил нагрузки и их моментов;
T
nn
qbqbqbB
2211
- вектор сил и моментов сил вязкого трения,
T
nn
qkqkqkK
2211
- вектор сил и моментов сил упругости.
77
Вычисление
вектора сил
инерции M
Вычисление
вектора
центробежных и
кориолисовых
сил S
Вычисление
вектора сил
тяжести G
U
1
,U
2
,U
3
m
1
,..., m
n
n
qq
,,
1
Φ
1i
,Φ
2i
,Φ
3i
i=1,..., n
n
qq
,,
1
g
Σ
-B
-K
Q
M
S
- G
Вычисление сил
внешней
нагрузкиF
- F
F
1i
,F
2i
,F
3i
i=1,..., n
1
2
1
2

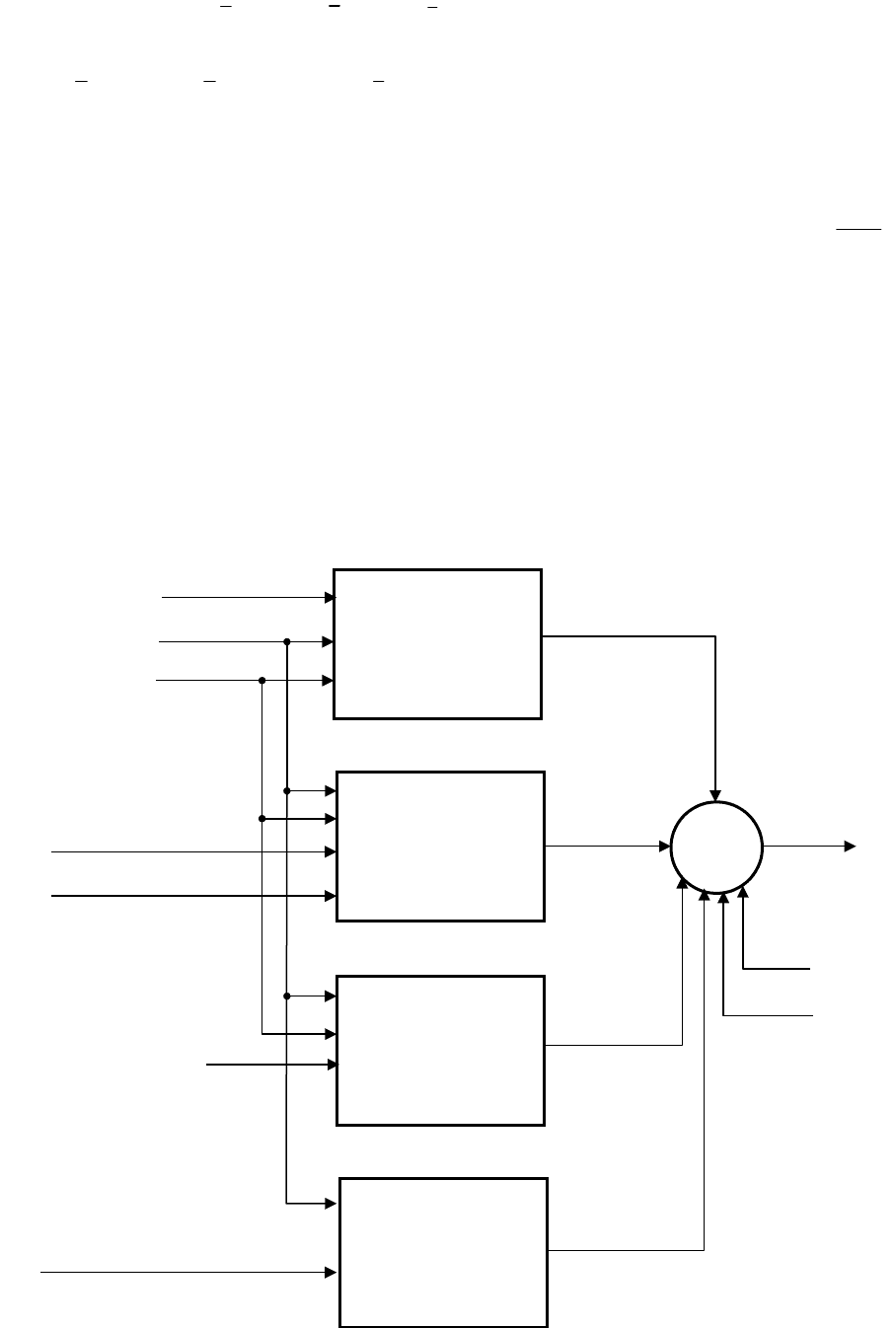
Рис. 3.22
Элементы векторов M, S, G и F будут равны:
n
i
iijiijiijij
zuyuxumM
1
321
, (3.60)
n
i
iijiijiijij
zuyuxumS
1
321
~
~~
, (3.61)
n
i
ijijijij
gugugumG
1
332211
, (3.62)
n
i
iijiijiijj
FuFuFuF
1
332211
, (3.63)
где
kij
u
- элементы матриц функциональных преобразователей U
k
; F
ki
–
координаты активных сил, приложенных к точке С
i
;
3,2,1k
,
nji ,,1,
.
Согласно поставленной задаче, векторы B и K полагаются известными.
Тогда общий алгоритм вывода уравнений динамики будет иметь
следующую структуру (рис. 3.22). Он экономно использует оперативную
память компьютера, что дает возможность выводить уравнения динамики
78
1
2
1
2

механических систем с большим числом степеней свободы при небольшом
объеме оперативной памяти. Алгоритмы вычисления векторов M, S, G и F
даны в приложении 2. Они основаны на использовании типовых
символьных операций умножения матрицы A (n x n) на вектор b (n x 1),
bAccc
T
n
1
, и суммирования элементов вектора c,
n
i
i
cc
1
[10].
Особенностью этих алгоритмов является то, что операция умножения на
ноль при их реализации не выполняется (на каждом шаге цикла
вычисляемому элементу присваивается значение «ноль»; если хотя бы
один множитель элемента равен нулю, то выполняется переход к
следующему шагу цикла).
Алгоритмы, реализующие вычисление компонент, обусловленных
инерцией звеньев относительно их центров масс, согласно формулам (3.9)
– (3.11), могут быть организованы аналогичным образом: с раздельным
вычислением составляющих, определяемых обобщенными скоростями,
ускорениями и внешней моментной нагрузкой относительно центров масс
звеньев.
3.9. Вычислительная эффективность алгоритмов
динамики
Реализация алгоритмов формирования уравнений динамики
механических систем, имеющих пространственную структуру и большое
число степеней свободы, требует сохранения в устройствах памяти
компьютера больших объемов данных и выполнения значительного числа
математических операций. Снижение затрат времени на выполнение
поставленной задачи может быть достигнуто за счет рационального
использования возможностей компьютера: уменьшения числа
необходимых математических операций, уменьшение числа обращений к
устройствам внешней памяти, учета особенностей архитектуры процессора
при разработке алгоритмов, использования сохраненных в ПЗУ
результатов предыдущих вычислений. Согласно [12], одним из важнейших
79
1
2
1
2
показателей вычислительной эффективности является число
математических операций сложения и умножения, требуемое для
реализации алгоритма
4
. По этому критерию предпочтительным будет тот
алгоритм, который требует меньшего объема вычислений для решения
одной и той же задачи.
Для алгоритмов динамики манипуляторов типовой задачей является
формирование уравнений динамики манипулятора, представляющего
собой разомкнутую кинематическую цепь без ветвлений, движущуюся в
однородном поле сил тяжести. Общее число операций умножения и
сложения, необходимых для вывода уравнений динамики такого
манипулятора с использованием алгоритма, разработанного на основе
метода связных графов
)()()()()()( nNnNnNnNnNnNSg
VGSMK
, (3.64)
где N
K
(n) – число операций, необходимых для формирования уравнений
кинематики; N
M
(n) – для вычисления вектора M инерционных компонент;
N
S
(n) - для вычисления вектора S центробежных и кориолисовых
компонент; N
G
(n) - для вычисления вектора G гравитационных компонент,
N
V
(n) - для вычисления инерционных компонент собственного вращения
звеньев; n – число степеней свободы манипулятора. Слагаемые в (3.64)
вычисляются по формулам:
,1,217366
,1,194
)(
nn
n
nN
K
(3.65)
nnnnN
M
6
1
2
9
3
11
)(
23
, (3.66)
nnnN
G
2
7
2
11
)(
2
, (3.67)
nnnnnN
V
55181212)(
234
, (3.68)
4
Алгоритм динамики предусматривает также символьное дифференцирование функций одного
аргумента. Но число операций символьного дифференцирования, по сравнению с числом
операций сложения и умножения, пренебрежимо мало.
80
1
2
1
2
