Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

A Survey of Geometric Vision 22

-13

22.3.2.1 Coplanar Features

The treatment for coplanar point features is similar to the general case. Assume the equation of the plane

in the ﬁrst camera frame is [π

, π

]X =0 with π

∈R

and π

∈R. By simply appending the 1 ×2block

[π

, π

]totheendofM in Equation (22.12), the rank condition in Theorem 22.1 still holds. Since

= N is the unit normal vector of the plane and π

=d is the distance from the ﬁrst camera center to

the plane, the rank condition implies d(



) − (N

)(



) =0, which is obviously equivalent to

the homography between the ith and the ﬁrst views (see Equation (22.8)). As for reconstruction, we can

use the four-point algorithm to initialize the estimation of the homography and then perform a similar

iteration scheme to obtain motion and structure. The algorithm can be found in [36, 51].

22.3.3 Further Readings

22.3.3.1 Multilinear Constraints and Factorization Algorithm

There are two other approaches dealing with multiple-view reconstruction. The ﬁrst approach is to use

the so-called multilinear constraints on multiple images of a 3-D point or line. For small number of views,

these constraints can be described in terms of tensorial notations [23, 52, 53]. For example, the constraints

for m = 3 can be described using trifocal tensors. For large number of views (m ≥ 5), the tensor is difﬁcult

to describe. The reconstruction is then to calculate the trifocal tensors ﬁrst and factorize the tensors for

camera motions [2]. An apparent disadvantage is that it is hard to choose the right “three-view sets” and

also difﬁcult to combine the results. Another approach is to apply some factorization scheme to iteratively

estimate the structure and motion [23, 40, 57], which is in the same spirit as Algorithm 22.2.

22.3.3.2 Universal Multiple-View Matrix and Rank Conditions

The reconstruction algorithm in this section was only for point features. Algorithms have also been

designed for lines features [35, 56]. In fact the multiple-view rank condition approach can be extended to

all different types of features such as line, plane, mixed line, point and even curves. This leads to a set of

rank conditions on a universal multiple-view matrix. For details please refer to [38, 40].

22.3.3.3 Dynamical Scenes

The constraint we developed in this section is for static scene. If the scene is dynamic, i.e., there are moving

objects in the scene, a similar type of rank condition can be obtained. This rank condition is obtained by

incorporating the dynamics of the objects in 3-D space into their own descriptions and lifting the 3-D

moving points into a higher dimensional space in which they are static. For details please refer to [27, 40].

22.3.3.4 Orthographic Projection

Finally, note that the linear algorithm and the rank condition are for the perspective projection model. If

the scene is far from the camera, then the image can be modeled using orthographic projection, and the

Tomasi-Kanade factorization method can be applied [59]. Similar factorization algorithm for other types

of projections and dynamics have also been developed [8, 21, 48, 49].

22.4 Utilizing Prior Knowledge of the Scene --- Symmetry

In this section we study how to incorporate scene knowledge into the reconstruction process. In our

daily life, especially in a man-made environment, there exist all types of “regularity.” For objects, regular

shapes such as rectangle, square, diamond, and circle always attract our attention. For spatial relationship

between objects, orthoganality, parallelism, and similarity are the conspicuous ones. Interestingly, all the

above regularities can be described using the notion of symmetry. For instance, a rectangular window

has one rotational symmetry and two reﬂective symmetry; the same windows on the same wall have

translational symmetry; the corner of a cube displays rotational symmetry.

-14 Robotics and Automation Handbook

22.4.1 Symmetric Multiple-View Rank Condition

There are many studies using instances of symmetry in the scene for reconstruction purposes [1, 3, 6, 19,

25, 28, 70, 73, 74]. Recently, a set of algorithms using symmetry for reconstruction from a single image

has been developed [25]. The main idea is to use the so-called equivalent images encoded in a single image

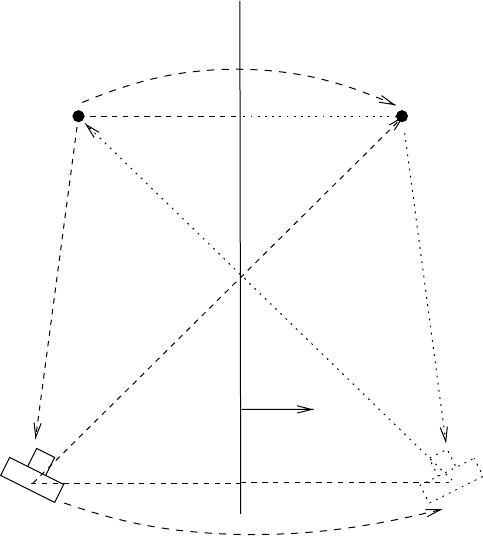
of a symmetric object. Figure 22.7 illustrates this notion for the case of a reﬂective symmetry. We attach

an object coordinate frame to the symmetric object and set it as the reference frame. 3-D points X and



are related by some symmetric transformation g (in the object frame) with g(X) = X



. If the image

is obtained from viewpoint O, then the image of X



can be interpreted as the image of X viewed from

the virtual viewpoint O



that is the correspondence of O under the same symmetry transformation g .

The image of X



is called an equivalent image of X viewed from O



. Therefore, given a single image of a

symmetric object, we have multiple equivalent images of this object. The number of all equivalent images

is the number of all symmetry of the object.

Inmodern mathematics, symmetry of an object are characterizedby a symmetrygroup with each element

in the group representing a transformation under which the object is invariant [25, 68]. For example, a

rectangle possesses two reﬂective symmetry and one rotational symmetry. We can use the group theoretic

notation to deﬁne a 3-D symmetric object as in [25].

Definition 22.1 Let S be a set of 3-D points. It is called a symmetric structure if there exists a non-trivial

subgroup G of the Euclidean group E (3) acting on S such that for any g ∈G, g deﬁnes an isomorphism

from S to itself. G is called the symmetry group of S.

′

¢ =

–1

′

FIGURE 22.7 X and X



are corresponding points under reﬂective symmetry transformation g (expressed in the

object frame) such that X



=g (X). N is the normal vector of the mirror plane. The motion between the camera frame

and the object frame is g

. Hence, the image of X



in real camera can be considered as the image of X viewed by a

virtual camera with pose g

g with respect to the object frame or g

−1

with respect to the real camera frame.

A Survey of Geometric Vision 22

-15

Under this deﬁnition, the possible symmetry on a 3-D object are reﬂective symmetry, translational

symmetry, rotational symmetry, and any combination of them. For any point p ∈S on the object, its

symmetric correspondence for g ∈G is g(p) ∈ S. The images of p and g (p) are denoted as x and g (x).

Let the symmetry transformation in the object frame be g = [R, T] ∈G (R ∈O(3) and T ∈R

As illustrated in Figure 22.7, if the transformation from the object (reference) frame to the real camera

frame is g

=[R

, T

], the transformation from the reference frame to the virtual camera frame is g

Furthermore, the transformation from the real camera frame to the virtual camera frame is



= g

−1

= [R



, T



] =





I − R



+ R



(22.19)

For the symmetric object S, assume its symmetry group G has m elements g

=[R

, T

], i =1, 2, ..., m.

Thenthetransformationbetween the ithvirtualcameraandtherealcamera is g



=[R



, T



](i =1, 2, ..., m)

as can be calculated from Equation (22.19). Given any point X ∈ S with image x and its equivalent images

(x)’s, we can deﬁne the symmetric multiple-view matrix

M(x

) =









(x)R





(x)T





(x)R





(x)T





(x)R





(x)T









(22.20)

According to Theorem 22.1, it satisﬁes the symmetric multiple-view rank condition:

rank(M(x)) ≤ 1

(22.21)

22.4.2 Reconstruction from Symmetry

Using the symmetric multiple-view rank condition and a set of n symmetric correspondences (points), we

can solve for g



=[R



, T



] and the structure of the points in S inthe object frame using an algorithm similar

to Algorithm 22.2. However, a further step is still necessary to recover g

=[R

, T

] for the camera pose

with respect to the object frame. This can be done by solving the following Lyapunov type of equations:



− g

= 0, or R



− R

R = 0 and T

= (I − R



)

†



− R

(22.22)

Since g



and g

are known, g

can be solved. The detailed treatment can be found in [25, 40].

As can be seen in the example at the end of this section, symmetry-based reconstruction is very accurate

and requires a minimum amount of data. A major reason is that the baseline between the real camera and

the virtual one is often large due to the symmetry transformation. Therefore, degenerate cases will occur if

the camera center is invariant under the symmetry transformation. For example, if the camera lies on the

mirror plane for a reﬂective symmetry, the structure can only be recovered up to some ambiguities [25].

The reconstruction for some special cases can be simpliﬁed without explicitly using the symmetric

multiple-view rank condition (e.g., see [3]). For the reﬂective symmetry, the structure with respect to the

camera frame can be calculated using only two pairs of symmetric points. Assume the image of two pairs

of reﬂective points are x, x



and y, y



. Then the image line connecting x and x



is obtained by l

∼





Similarly, l

connecting y and y



satisﬁes l

∼





. It can be shown that the unit normal vector N (see

Figure 22.7) of the reﬂection plane satisﬁes





N = 0 (22.23)

from which N can be solved. Assume the depth of x and x



are λ and λ



, then they can be calculated using

-16 Robotics and Automation Handbook

the following relationship





Nx −





x N













(22.24)

where d is the distance from the camera center to the reﬂection plane.

22.4.2.1 Planar Symmetry

Planar symmetric objects are widely present in man-made environment. Regular shapes such as square and

rectangle are often good landmarks for mapping and recognition tasks. For a planar symmetric object,

its symmetry forms a subgroup G of E (22.2) instead of E (22.3). Let g ∈ E (2) be one symmetry of a

planar symmetric object. Recall that there exists a homography H

between the object frame and camera

frame. Also between the original image and the equivalent image generated by g, there exists another

homography H. It can be shown that H = H

−1

. Therefore all the homographies generated from the

equivalent images form a homography group H

−1

,whichisconjugatetoG [3]. This fact can be used

in testing if an image is the image of an object with desired symmetry. Given the image, by calculating the

homographies from all equivalent images based on the hypothesis, we can check the group relationship

of the homography group and decide if the desired symmetry exists [3]. In case the object is a rectangle,

the calculation can be further simpliﬁed using the notion of vanishing point as illustrated in the following

example.

Example 22.3 (Symmetry-based reconstruction for a rectangular object.)

For a rectangle in 3-D space, the two pairs of parallel edges generate two vanishing points v

and v

in the

image. As a 3-D vector, v

(i =1, 2) can also be interpreted as the vector from the camera center to the

vanishing point and hence must be parallel to the pair of parallel edges. Therefore, we must have v

⊥ v

So by checking the angle between the two vanishing points, we can decide if a region can be the image of

a rectangle. Figure 22.8 demonstrates the reconstruction based on the assumption of a rectangle. The two

sides of the cube are two rectangles (in fact squares). The angles between the vanishing points are 89.1

◦

and 92.5

◦

, respectively. The reconstruction is performed using only one image and six points. The angle

between the two planes is 89.2

◦

22.4.3 Further Readings

22.4.3.1 Symmetry and Vision

Symmetry is a strong vision cue in human vision perception and has been extensively discussed in psychol-

ogy and cognition research [43, 45, 47]. It has been noticed that symmetry is useful for face recognition

[61, 62, 63].

22.4.3.2 Symmetry in Statistical Context

Besides geometric symmetry that has been discussed in this section, symmetry in the sense of statistics have

also been studied and utilized. Actually, the computational advantages of symmetry were ﬁrst explored in

the statistical context, such as the study of isotropic texture [17, 42, 69]. It was the work of [14, 15, 42] that

provided a wide range of efﬁcient algorithms for recovering the orientation of a textured plane based on

the assumption of isotropy or weak isotropy.

22.4.3.3 Symmetry of Surfaces and Curves

While we only utilized symmetric points in this chapter, the symmetry of surfaces has also been exploited.

References [55, 72] used the surface symmetry for human face reconstruction. References [19, 25] studied

reconstruction of symmetric curves.

A Survey of Geometric Vision 22

-17

FIGURE 22.8 Reconstruction from a single view of the cube with six corner points marked. An arbitrary view, a

side view, and a bird view of the reconstructed and rendered rectangles are displayed. The coordinate frame shows the

recovered camera pose.

22.5 Comprehensive Examples and Experiments

Finally,wediscussseveral applications ofusingthe techniquesintroducedin this chapter. These applications

all involve reconstruction from a single or multiple images for the purpose of robotic navigation and

mapping. While not all of them are fully automatic, they demonstrate the potential of the techniques

discussed in this chapter and some future directions for improvement.

22.5.1 Automatic Landing of Unmanned Aerial Vehicles

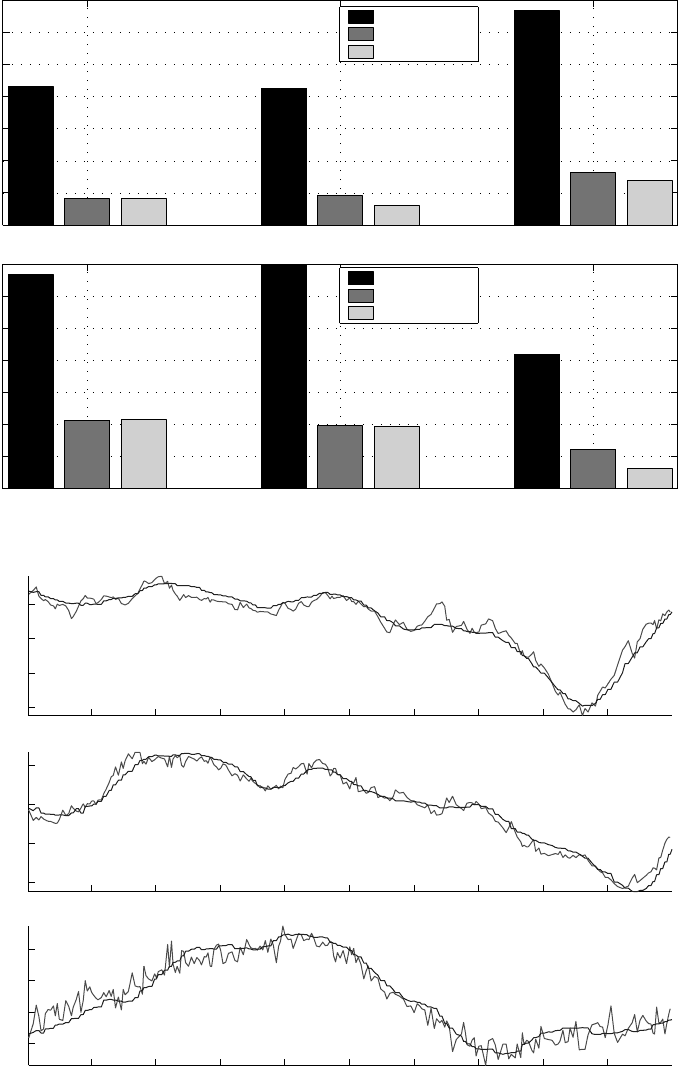
Figure 22.9 displays the experiment setup for applying the multiple-view rank condition based algorithm

in automatic landing of UAV in University of California at Berkeley [51]. In this experiment, the UAV is

a model helicopter (Figure 22.9, top) with an on-board video camera facing downwards searching for the

landing pad (Figure 22.9, bottom left) on the ground. When the landing pad is found, corner points are

extracted from each image in the video sequence (Figure 22.9, bottom right). The pose and the motion

of the camera (and the UAV) are estimated using the feature points in the images. Previously the four-

point two-view reconstruction algorithm for planar features was tested. However, its results were noisy

(Figure 22.10, top). Later a nonlinear two-view algorithm was developed, but it was time consuming.

Finally, by adopting the rank condition based multiple-view algorithm, the landing problem was solved.

The multiple-view reconstruction is performed at 10 Hz for every four images. The algorithm is a

modiﬁcation of the Algorithm 22.2 introduced in this chapter, which is speciﬁcally designed for coplanar

features. Figure 22.10 shows the comparison of this algorithm with other algorithms and sensors. The

multiple-view algorithm is more accurate than either two-view algorithm (Figure 22.10, top) and is close

-18 Robotics and Automation Handbook

FIGURE 22.9 Top: A picture of the UAV in landing process. Bottom left: An image of the landing pad viewed from

an on-board camera. Bottom right: Extracted corner features from the image of the landing pad. (Photo courtesy of

O. Shankeria.)

to the results obtained from differential GPS and INS sensors (Figure 22.10, bottom). The overall error

for this algorithm is less than 5 cm in distance and 4

◦

for rotation [51].

22.5.2 Automatic Symmetry Cell Detection, Matching and Reconstruction

In Section 22.4, we discussed symmetry-based reconstruction techniques from a single image. Here we

present a comprehensive example that performs symmetry-based reconstruction from multiple views

[3, 28]. In this example, the image primitives are no longer point or line. Instead we use the symmetry cells

as features. The example includes three steps.

22.5.2.1 Feature Extraction

By symmetry cell we mean a region in the image that is an image of a desired symmetric object in 3-D. In

this example, the symmetric object we choose is rectangle. So the symmetry cells are images of rectangles.

Detecting symmetry cells (rectangles) includes two steps. First, we perform color-based segmentation on

the image. Then, for all the detected four-sided regions, we test if its two vanishing points are perpendicular

to each other and decide if it can be an image of a rectangle in 3-D space. Figure 22.11 demonstrates this

for the picture of an indoor scene. In this picture, after color segmentation, all four-sided regions with

reasonablesizes aredetectedand markedwithdarkenedboundaries. Then each four-sidedpolygonispassed

through the vanishing point test. For those polygons passing the test, we denote them as symmetry cells and

recover the object frames with the symmetry-based algorithm. Each individual symmetry cell is recovered

A Survey of Geometric Vision 22

-19

X Y Z

Comparison of Motion Estimation Algorithms

Translation error (cm)

linear 2-view

nonlinear

multi-view

X Y Z

Rotation error (degrees)

linear 2-view

nonlinear

multi-view

2 4 6 8 10 12 14 16 18

64.2

64.4

64.6

64.8

x–pos (m)

2 4 6 8 10 12 14 16 18

–56.8

–56.6

–56.4

–56.2

y–pos (m)

z–pos (m)

2 4 6 8 10 12 14 16 18

–3.4

–3.2

–3

–2.8

time (seconds)

Multi–View State Estimate (red) vs INS/GPS State (blue)

FIGURE 22.10 Top:Comparison of the multiple-view rank condition based algorithm with two-viewlinear algorithm

and nonlinear algorithm. Bottom: Comparison of the results from multiple-view rank condition based algorithm (red

line) with GPS and INS results (blue line). (Image courtesy of O. Shankeria.)

-20 Robotics and Automation Handbook

FIGURE 22.11 Left: original image. Middle: image segmentation and polygon ﬁtting. Right: symmetry cells detected

and extracted — an object coordinate frame is attached to each symmetry cell.

with a different scale. Please note that this test is a hypothesis testing step, it cannot verify if the object in 3-D

is actually a desired symmetric object, instead it can conﬁrm that its image satisﬁes the condition of the test.

22.5.2.2 Feature Matching

Foreach cell we can calculate its 3-D shape. Then for two cells in two images, by comparing their 3-D shapes

and colors, we can decide if they are matchingcandidates. In the case of existenceof many similar symmetry

cells, we need to use a matching graph [28]; that is, set the nodes of the graph to be all pairs of possible

matched cells across the two images. For each pair of matched pair, we can calculate a camera motion

between the two views; then correct matching should generate the same (up to scale) camera motion. We

draw an edge between two nodes if these two pairs of matched cells generate similar camera motions.

Therefore, the problem of ﬁnding the correctly matched cells becomes the problem of ﬁnding the (maxi-

mum) cliques in the matching graph. Figure 22.12 shows the matching results for two cells in three images.

The cells that have no match in other images are discarded. The scales for all pairs of matched cells are

uniﬁed.

22.5.2.3 Reconstruction

Given the set of correctly matched cells, only one more step is needed for reconstruction. Note that the

camera motions from different pairs of matched cells have different scales. To unify the scale, we pick

one pair of matched cells as the reference to calculate the translation and use this translation to scale the

remaining matched pairs. The new scales can further be passed to resize the cells. Figure 22.13 shows the

reconstructed 3-D cells and the camera poses for the three views. The physical dimension of the cells are

calculated with good accuracy. The aspect ratios for the white board and the table top are calculated as

1.51 and 1.01, respectively, with the ground truth being 1.50 and 1.00.

In this example, all the features are matched correctly without any manual intervention. Please note

that establishing feature matching among the three views using other approaches would otherwise be very

difﬁcult due to the large baseline between the ﬁrst and second images and the pure rotational motion

FIGURE 22.12 Two symmetry cells are matched in three images. From the raw images, symmetry cell extraction, to

cell matching, the process needs no manual intervention.

A Survey of Geometric Vision 22

-21

FIGURE 22.13 Camera poses and cell structure recovered. From left to right: top, side, and frontal views of the cells

and camera poses.

between the second and third images. For applications such as robotic mapping, the symmetric cells can

serve as “landmarks.” The pose and motion of the robot can be easily derived using a similar scheme.

22.5.3 Semiautomatic Building Mapping and Reconstruction

If a large number of similar objects is present, it is usually hard for the detection and matching scheme

in the above example to work properly. For instance, for the symmetry of window complexes on the side

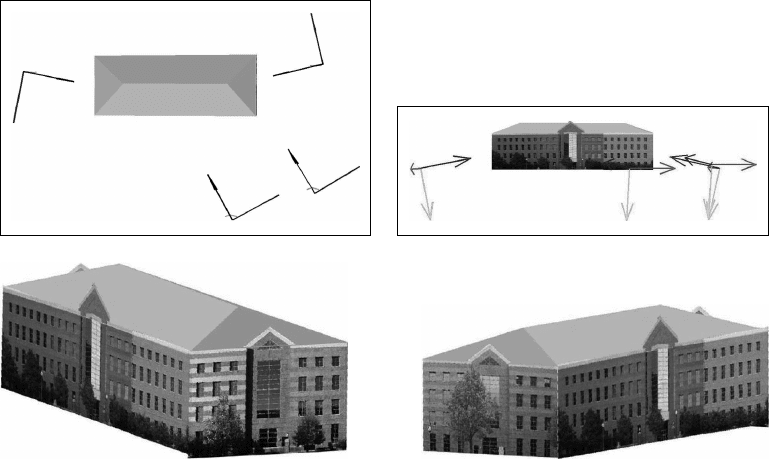
of a building shown in Figure 22.14, many ambiguous matches may occur. In such cases, we need to take

manual intervention to obtain a realistic 3-D reconstruction (e.g., see [28]). The techniques discussed

so far, however, help to minimize the amount of manual intervention. For images in Figure 22.14, the

user only needs to point out cells and provide the cell correspondence information. The system will then

automatically generate a consistent set of camera poses from the matched cells, as displayed in Figure 22.15

FIGURE 22.14 Five images used for reconstruction of a building. For the ﬁrst four image, we mark a few cells

manually. The last image is only used for extracting roof information.

-22 Robotics and Automation Handbook

FIGURE 22.15 Top: The recovered camera poses and viewpoints as well as the cells. The four coordinate frames are

the recovered camera poses from the four images in Figure 22.14. The roof was substituted by a “virtual” one based

on corners extracted from the ﬁfth image in Figure 22.14 using the symmetry-based algorithm. Blue arrows are the

camera optical axes. Bottom: 3-D model of the building reconstructed from the original set of four images.

top. For each cell, a camera pose is recovered using the symmetry-based algorithm. Similar to the previous

example, motion between cameras can be recovered using the corresponding cell. When the camera poses

are recovered, the 3-D structure of the building can be recovered as shown in Figure 22.15 bottom. The 3-D

model is rendered as piecewise planar parts. The angles between the normal vectors of any two orthogonal

walls differ from 90

◦

by an average of 1

◦

error without any nonlinear optimization. The whole process

(from taking the images to 3-D rendering) takes less than 20 min.

22.5.4 Summary

The above examples demonstrate the potential of the theory and algorithms introduced in this chapter.

Besides these examples, we can expect that these techniques will be very useful in many other applications

such as surveillance, manipulation, navigation, and vision-based control. Finally, we like to point out that

we are merely at the beginning stage of understanding the geometry and dynamics associated with visual

perception. Much of the topological, geometric, metric, and dynamical relations between 3-D space and

2-D images is still largely unknown, which, to some extent, explains why the capability of existing machine

vision systems is still far inferior to that of human vision.

References

[1] Francois, A.R.J., Medioni, G.G., and Waupotitsch, R., Reconstructing mirror symmetric scenes

from a single view using 2-view stereo geometry, in Proc. Int. Conf. Pattern Recognition, pp. 40012–

40015, 2002.

[2] Avidan, S. and Shashua, A., Novel view synthesis by cascading trilinear tensors, IEEE Trans. Visual-

ization and Computer Graphics, 4(4):293–306, 1998.

[3] Yang, A.Y., Rao, S., Huang, K., Hong, W., and Ma, Y., Geometric segmentation of perspective images

based on symmetry groups, in Proc. IEEE Int. Conf. Computer Vision, Nice, France, Vol. 2, pp.

1251–1258, 2003.