Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

-18 Robotics and Automation Handbook

the latter term following since θ is constant, i.e.,

θ =

θ. Using the parameter update law (17.102) gives

V =−e

Qe (17.105)

From this it follows that the position tracking errors converge to zero asymptotically and the parameter

estimation errors remain bounded. Furthermore, it can be shown that the estimated parameters converge

to the true parameters provided the reference trajectory satisﬁes the condition of persistency of excitation,

αI ≤



)Y(q

)dt ≤ β I

(17.106)

for all t

,whereα, β, and T are positive constants.

In order to implement this adaptive feedback linearization scheme, however, one notes that the accel-

eration

q is needed in the parameter update law and that

M must be guaranteed to be invertible, possibly

by the use of projection in the parameter space. Later work was devoted to overcome these two drawbacks

to this scheme by using so-called indirect approaches based on a (ﬁltered) prediction error.

17.3.7 Passivity-Based Approaches

One may also exploit the passivity of the rigid robot dynamics to derive robust and adaptive control

algorithms for manipulators. These methods are qualitatively different from the previous methods which

were based on feedback linearization. In the passivity-based approach, we modify the inner loop control

τ =

M(q)a +

C(q,

q)v +

g(q) − Kr

(17.107)

where v, a, and r are given as

v =

− 



a =

v =

− 



r =

− v =



q + 



with K ,  diagonal matrices of positive gains. In terms of the linear parametrization of the robot dynamics,

the control (17.107) becomes

τ = Y(q,

q, a, v)

θ − Kr

(17.108)

and the combination of Equation (17.107) with Equation (17.41) yields

M(q)

r +C(q,

q)r + Kr = Y

(17.109)

Note that, unlike the inverse dynamics control, the modiﬁed inner loop control (17.41) does not achieve

a linear, decoupled system, even in the known parameter case

θ = θ . However, in this formulation the

regressor Y in Equation (17.109) does not contain the acceleration

q nor is the inverse of the estimated

inertia matrix required. These represent distinct advantages over the feedback linearization based schemes.

17.3.8 Passivity-Based Robust Control

In the robust passivity-based approach of [36], the term

θ in Equation (17.108) is chosen as

θ = θ

+ u (17.110)

where θ

is a ﬁxed nominal parameter vector and u is an additional control term. The system (17.109)

then becomes

M(q)

r +C(q,

q)r + Kr = Y(a, v, q,

q)(

θ +u)

(17.111)

Robust and Adaptive Motion Control of Manipulators 17

-19

where

θ = θ

− θ is a constant vector and represents the parametric uncertainty in the system. If the

uncertainty can be bounded by ﬁnding a nonnegative constant, ρ ≥ 0, such that



θ=θ

− θ ≤ρ (17.112)

then the additional term u can be designed according to the expression,

u =







−ρ

||Y

r ||

,if||Y

r || >

−



r,if||Y

r || ≤ 

(17.113)

The Lyapunov function

V =

M(q)r +



K



q (17.114)

is used to show uniform ultimate boundedness of the tracking error. Note that

θ is constant and so is not

a state vector as in adaptive control. Calculating

V yields

V =r

r +

Mr + 2



K



q (17.115)

=−r

Kr + 2



K



q +

(

M − 2C)r + r

θ +u) (17.116)

Using the passivity property and the deﬁnition of r, this reduces to

V =−





K 



q −



q +r

θ +u)

(17.117)

Uniform ultimate boundedness of the tracking error follows with the control u from (17.113). See [36]

for details.

Comparing this approach with the approach in the section (17.3.5), we see that ﬁnding a constant bound

ρ for the constant vector

θ is much simpler than ﬁnding a time-varying bound for η in Equation (17.44).

The bound ρ in this case depends only on the inertia parameters of the manipulator, while ρ(x, t)in

Equation (17.69) depends on the manipulator state vector and the reference trajectory and, in addition,

requires some assumptions on the estimated inertia matrix

M(q).

17.3.9 Passivity-Based Adaptive Control

In the adaptive approach the vector

θ in Equation (17.109) is now taken to be a time-varying estimate of

the true parameter vector θ. Combining the control law (17.107) with (17.41) yields

M(q)

r +C(q,

q)r + Kr = Y

(17.118)

The parameter estimate

θ may be computed using standard methods such as gradient or least squares. For

example, using the gradient update law



θ =−

−1

(q,

q, a, v)r (17.119)

together with the Lyapunov function

V =

M(q)r +



K



q +



(17.120)

results in global convergence of the tracking errors to zero and boundedness of the parameter estimates

since

V =−





K 



q −



q +

{

θ + Y

r } (17.121)

See [38] for details.

-20 Robotics and Automation Handbook

PERFORMANCE

MEASURE

CONTROL

ROBOT

MODEL

–

min J

(

)

•

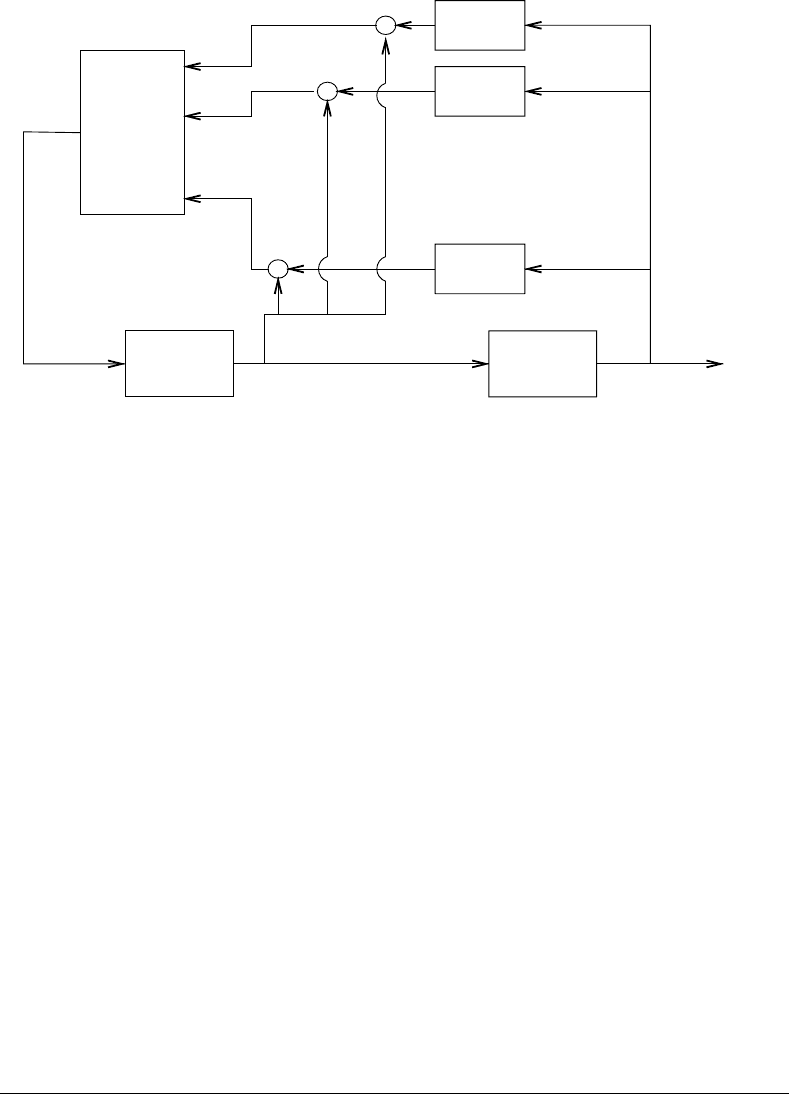
FIGURE 17.9 Multiple-model-based hybrid control architecture.

17.3.10 Hybrid Control

A Hybrid System is one that has both continuous-time and discrete-event or logic-based dynamics.

Supervisory Control, Logic-Based Switching Control, and Multiple-Model Control are typical control

architectures in this context. In the robotics context, hybrid schemes can be combined with robust and

adaptive control methods to further improve robustness. In particular, because the preceeding robust and

adaptivecontrolmethods provide only asymptotic (i.e., as t →∞)error bounds, the transientperformance

may not be acceptable. Hybrid control methods have been shown to improve transient performance over

ﬁxed robust and adaptive controllers.

The use of the term Hybrid Control in this context should not be confused with the notion of Hybrid

Position/Force Control [41]. The latter is a familiar approach to force control of manipulators in which

the term hybrid refers to the combination of pure force control and pure motion control.

Figure 17.9 shows the Multiple-Model approach of [12], which has been applied to the adaptive control

of manipulators. In this architecture, the multiple models have the same structure but may have different

nominal parameters in case a robust control scheme is used, or different initial parameter estimates if

an adaptive control scheme is used. Because all models have the same inputs and desired outputs, the

identiﬁcation errors e

are available at each instant for the jth model. The idea is then to deﬁne a

performance measure, for example,

J (e

(t)) = γ e

(t) + β



(σ )dσ with γ, β>0 (17.122)

and switch into the closed loop the control input that results in the smallest value of J at each instant.

17.4 Conclusions

We have given a brief overview of the basic results in robust and adaptive control of robot manipulators.

In most cases, we have given only the simplest forms of the algorithms, both for ease of exposition and

for reasons of space. An extensive literature is available that contains numerous extensions of these basic

results. The attached list of references is by no means an exhaustive one. The book [10] is an excellent and

Robust and Adaptive Motion Control of Manipulators 17

-21

highly detailed treatment of the subject and a good starting point for further reading. Also, the reprint

book [37] contains several of the original sources of material surveyed here. In addition, the two survey

papers [1] and [28] provide additional details on the robust and adaptive control outlined here.

Several important areas of interest have been omitted for space reasons including output feedback

control, learning control, fuzzy control, neural networks, and visual servoing, and control of ﬂexible

robots. The reader should consult the references at the end for background on these and other subjects.

References

[1] Abdallah, C. et al., Survey of robust control for rigid robots, IEEE Control Systems Magazine, Vol. 11,

No.2,pp.24–30, Feb. 1991.

[2] Amestegui, M., Ortega, R., and Ibarra, J.M., Adaptive linearizing-decoupling robot control: A com-

parative study, Proc. 5th Yale Workshop on Applications of Adaptive Systems Theory, NewHaven,CT,

1987.

[3] Balestrino, A., De Maria, G., and Sciavicco, L., An adaptive model following control for robotic

manipulators, ASME J. Dynamic Syst., Meas., Contr., Vol. 105, pp. 143–151, 1983.

[4] Bayard, D.S. and Wen, J.T., A new class of control laws for robotic manipulators-Part 2. Adaptive

case, Int. J. Contr., Vol. 47, No. 5, pp. 1387–1406, 1988.

[5] Becker, N. and Grimm, W.M., On L

and L

∞

-stability approaches for the robust control of robot

manipulators, IEEE Trans. Automat. Contr., Vol. 33, No. 1, pp. 118–122, Jan. 1988.

[6] Berghuis, H. and Nijmeijer, H., Global regulation of robots using only position measurements, Syst.

Contr. Lett., Vol. 1, pp. 289–293, 1993.

[7] Berghuis, H., Ortega, R., and Nijmeier, H., A robust adaptive robot controller, IEEE Trans. Robotics

Automat., Vol. 9, No. 6, pp.825–830, Dec. 1993.

[8] Brogliato, B., Landau, I.D., and Lozano, R., Adaptive motion control of robot manipulators: A

uniﬁed approach based on passivity, Int. J. Robust Nonlinear Contr., Vol. 1, pp. 187–202, 1991.

[9] Campion, G. and Bastin, G., Analysis of an adaptive controller for manipulators: Robustness versus

ﬂexibility, Syst. Contr. Lett., Vol. 12, pp. 251–258, 1989.

[10] Canudas de Wit, C. et al., Theory of Robot Control, Springer-Verlag, London, 1996.

[11] Canudas de Wit, C. and Fixot, N., Adaptive control of robot manipulators via velocity estimated

state feedback, IEEE Trans. Automatic Contr., Vol. 37, pp. 1234–1237, 1992.

[12] Ciliz, M.K. and Narendra, K.S., Intelligent control of robotic manipulators: A multiple model based

approach, IEEE Conf. on Decision and Control, New Orleans, LA, pp. 422–427, December 1995.

[13] Corless, M. and Leitmann, G., Continuous state feedback guaranteeing uniform ultimate bound-

edness for uncertain dynamic systems, IEEE Trans. Automatic Contr., Vol. 26, pp. 1139–1144, 1981.

[14] Craig, J.J., Adaptive Control of Mechanical Manipulators, Addison-Wesley, Reading, MA, 1988.

[15] Craig, J.J., Hsu, P., and Sastry, S., Adaptive control of mechanical manipulators, Proc. IEEE Int. Conf.

Robotics Automation, San Francisco, CA, March 1986.

[16] De Luca, A., Dynamic control of robots with joint elasticity, Proc. IEEE Conf. on Robotics and

Automation, Philadelphia, PA, pp. 152–158, 1988.

[17] Desoer, C.A. and Vidyasagar, M., Feedback Systems: Input-Output Properties, Academic Press, New

York, 1975.

[18] Filippov, A.F., Differential equations with discontinuous right-hand side, Amer. Math. Soc. Transl.,

Vol. 42, pp. 199–231, 1964.

[19] Hager, G.D., A modular system for robust positioning using feedback from stereo vision, IEEE Trans.

Robotics Automat., Vol. 13, No. 4, pp. 582–595, August 1997.

[20] Ioannou, P.A. and Kokotovi

c, P.V., Instability analysis and improvement of robustness of adaptive

control, Automatica, Vol. 20, No. 5, pp. 583–594, 1984.

[21] Khatib, O., A uniﬁed approach for motion and force control of robot manipulators: the operational

space formulation, IEEE J. Robotics Automat., Vol. RA–3,No.1,pp.43–53, Feb. 1987.

-22 Robotics and Automation Handbook

[22] Kim, Y.H. and Lewis, F.L., Optimal design of CMAC neural-network controller for robot manipu-

lators, IEEE Trans. on Sys. Man and Cybernetics, Vol. 30, No. 1, pp. 22–31, Feb. 2000.

[23] Koditschek, D., Natural motion of robot arms, Proc. IEEE Conf. on Decision and Control, Las Vegas,

NV, pp. 733–735, 1984.

[24] Kreutz, K., On manipulator control by exact linearization, IEEE Trans. Automat. Contr., Vol. 34,

No.7,pp.763–767, July 1989.

[25] Latombe, J.C., Robot Motion Planning, Kluwer, Boston, MA, 1990.

[26] Luh, J., Walker, M., and Paul, R., Resolved-acceleration control of mechanical manipulators, IEEE

Trans. Automat. Contr., Vol. AC–25, pp. 468–474, 1980.

[27] Middleton, R.H. and Goodwin, G.C., Adaptive computedtorque controlfor rigid link manipulators,

Syst. Contr. Lett., Vol. 10, pp. 9–16, 1988.

[28] Ortega, R. and Spong, M.W., Adaptive control of rigid robots: a tutorial, Proc. IEEE Conf. on Decision

and Control, Austin, TX, pp. 1575–1584, 1988.

[29] Paul, R.C., Modeling, trajectory calculation, and servoing of a computer controlled arm, Stanford

A.I. Lab, A.I. Memo 177, Stanford, CA, Nov. 1972.

[30] Dahleh, M.A. and Pearson, J.B., L

-optimal compensators for continuous-time systems, IEEE Trans.

Automat. Contr., Vol. AC-32, No. 10, pp. 889–895, Oct. 1987.

[31] Porter, D.W. and Michel, A.N., Input-output stability of time varying nonlinear multiloop feedback

systems, IEEE Trans. Automat. Contr., Vol. AC-19, No. 4, pp. 422–427, Aug. 1974.

[32] Sadegh, N. and Horowitz, R., An exponentially stable adaptive control law for robotic manipulators,

Proc. American Control Conf., San Diego, pp. 2771–2777, May 1990.

[33] Schwartz, H.M. and Warshaw, G., On the richness condition for robot adaptive control, ASME

Winter Annual Meeting, DSC-Vol. 14, pp. 43–49, Dec. 1989.

[34] Slotine, J.-J.E. and Li, W., On the adaptive control of robot manipulators, Int. J. Robotics Res., Vol. 6,

No.3,pp.49–59, 1987.

[35] Spong, M.W., Modeling and control of elastic joint manipulators, J. Dyn. Sys., Meas. Contr., Vol. 109,

pp. 310–319, 1987.

[36] Spong, M.W., On the robust control of robot manipulators, IEEE Trans. Automat. Contr., Vol. 37,

pp. 1782–1786, Nov. 1992.

[37] Spong, M.W., Lewis, F., and Abdallah, C., Robot Control: Dynamics, Motion Planning, and Analysis,

IEEE Press, 1992.

[38] Spong, M.W., Ortega, R., and Kelly, R., Comments on ‘Adaptive manipulator control’, IEEE Trans.

Automat. Contr., Vol. AC–35, No. 6, pp. 761–762, 1990.

[39] Spong, M.W. and Vidyasagar, M., Robust nonlinear control of robot manipulators, Proc. 24th IEEE

Conf. Decision and Contr., Fort Lauderdale, FL, pp. 1767–1772, Dec. 1985.

[40] Spong, M.W. and Vidyasagar, M., Robust linear compensator design for nonlinear robotic control,

IEEE J. Robotics Automation, Vol. RA-3, No. 4, pp. 345–350, Aug. 1987.

[41] Spong, M.W. and Vidyasagar, M., Robot Dynamics and Control, John Wiley & Sons, New York,

1989.

[42] Su, C.-Y., Leung, T.P., and Zhou, Q.-J., A novel variable structure control scheme for robot trajectory

control, IFAC World Congress, Vol. 9, pp. 121–124, Tallin, Estonia, August 1990.

[43] Vidyasagar, M., Control Systems Synthesis: A Factorization Approach, MIT Press, Cambridge, MA,

1985.

[44] Vidyasagar, M., Optimal rejection of persistent bounded disturbances, IEEE Trans. Automat. Contr.,

Vol. AC–31, No. 6, pp. 527–534, June 1986.

[45] Yaz, E., Comments on On the robust control of robot manipulators by M.W. Spong, IEEE Trans.

Automatic Control, Vol. 38, No. 3, pp. 511–512, Mar. 1993.

[46] Yoo, B.K. and Ham, W.C., Adaptive control of robot manipulator using fuzzy compensator, IEEE

Trans. on Fuzzy Systems, Vol. 8, No. 2, pp. 186–199, Apr. 2000.

[47] Yoshikawa, T., Foundations of Robotics: Analysis and Control, MIT Press, Cambridge, MA, 1990.

Robust and Adaptive Motion Control of Manipulators 17

-23

[48] Youla, D.C.,Jabr, H.A., and Bongiorno, J.J., Modern Wiener-Hopf design of optimal controllers–Part

2: the multivariable case, IEEE Trans. Automatic Control, Vol. AC-21, pp. 319–338, June 1976.

[49] Zhang, F., Dawson, D.M., deQueiroz, M.S., and Dixon, W.E., Global adaptive output feedback

tracking control of robot manipulators, IEEE Trans. Automat. Contr., Vol. AC–45, No. 6, pp. 1203–

1208, June 2000.

Sliding Mode

Control of Robotic

Manipulators

Hector M. Gutierrez

Florida Institute of Technology

18.1 Sliding Mode Controller Design–An Overview

18.2 The Sliding Mode Formulation of the Robot

Manipulator Motion Control Problem

18.3 Equivalent Control and Chatter Free Sliding

Control

18.4 Control of Robotic Manipulators by Continuous

Sliding Mode Laws

Sliding Mode Formulation of the Robotic Manipulator Motion

Control Problem

•

Sliding Mode Controller Design

18.5 Conclusions

18.1 Sliding Mode Controller Design -- An Overview

Sliding mode design [1–6] has several features that make it an attractive technique to solve tracking

problemsin motion control of robotic manipulators, the most importantbeing its robustnessto parametric

uncertainties and unmodelled dynamics, and the computational simplicity of the algorithm. One way of

looking at sliding mode controller design is to think of the design process as a two-step procedure. First, a

region of the state space where the system behaves as desired (sliding surface) is deﬁned. Then, a control

action that takes the system into such surface and keeps it there is to be determined. Robustness is usually

achieved based on a switching control law. The design of the control action can be based on different

strategies, a straightforward one being to deﬁne a condition that makes the sliding surface an attractive

region for the state vector trajectories. Consider a nonlinear afﬁne system of the form:

)

= f

(x) +



j=1

(x)u

, i = 1, ..., m, j = 1, ..., m (18.1)

where u = [u

, ..., u

]

is the vector of m control inputs, and the state x is composed of the x

coordinates

to be tracked and their ﬁrst (n

− 1) derivatives. Such systems are called square systems because they

have as many control inputs u

as outputs to be controlled x

[3]. The motion control problem to be

addressed is the one of making the state vector x track a desired trajectory r. Consider ﬁrst the time-varying

manifoldσ givenbytheintersectionofthesurfacess

(x, t) =0, i =1, ..., m, speciﬁed bythe componentsof

-2 Robotics and Automation Handbook

S(x, t) = [s

(x, t), ..., s

(x, t)]

,where

s(x, t) =



+ λ



−1

−r

) = 0 (18.2)

whichcan becomputedfrom x and r , λ

beingsomepositiveconstant.Suchmanifoldis usually called sliding

surface; any state trajectory lying on it tracks the reference r since Equation (18.2) deﬁnes a differential

equationon theerror vectorthat stably convergesto zero. Anintegral term can be incorporated to the sliding

surface to further penalize tracking error. For instance, Equation (18.2) can be rewritten for n

= 3as

s(x, t) =



+ λ









−r

)dt





= (

−

) +2λ

−r

) +λ



−r

)dt = 0 (18.3)

There are also several possible strategies to design the control action u

that takes the system to the sliding

surface. One such strategy is to ﬁnd u

in a way that each component of the sliding surface s

is an attractive

region of the state space by forcing the control action to satisfy a geometric condition such as





≤−η

|⇔s

≤−η

|≤0 (18.4)

whereη

is a strictly positiveconstant.This conditionforcesthe squared distance tothe surface (as measured

by s

) to decrease along all state trajectories [3]. In other words, all the state trajectories are constrained

to point toward σ . A simple solution that satisﬁes the sliding condition (18.4) in spite of the uncertainty

on the dynamics (18.1) is the switching control law:

= k(x, t)sgn(s ), sgn(s ) =



1, s > 0

−1, s < 0

(18.5)

The gain k(x, t) of this inﬁnitely fast switching control law increases with the extent of parametric un-

certainty, introducing a discontinuity in the control signal called chatter. This is an obviously undesirable

practical problem that will be discussed in Section 18.3.

18.2 The Sliding Mode Formulation of the Robot

Manipulator Motion Control Problem

The sliding mode formulation of the robot manipulator motion control problem starts from the basic

dynamic equations that link the input torques to the vector of robot joint coordinates:

H(q)

q + g (q, t) = τ

(18.6)

where τ is the n × 1 vector of input torques, q is the n × 1 vector of joint coordinates, H(q) is the

n ×n diagonal positive deﬁnite inertia matrix, and g (q, t)isthen ×1 load vector that describes all other

mechanical effects acting on the robot. This basic formulation can be expanded to describe more speciﬁc

motion control problems, e.g., for an ideal rigid-link rigid-joint robot with n links interacting with the

environment [7]:

H(q)

q + c(q,

q) + g (q) − J

(q)F = τ (18.7)

where c(q,

q)isann × 1 vector of centrifugal/Coriolis terms, g (q) is the n × 1 vector of gravitational

forces, J

(q)isthen × m transpose of the robot’s Jacobian matrix, and F is the m × 1vectorofforces

that the (m-dimensional) environment exerts in the robot end-effector. The motion control problem is

Sliding Mode Control of Robotic Manipulators 18

-3

constrain surface

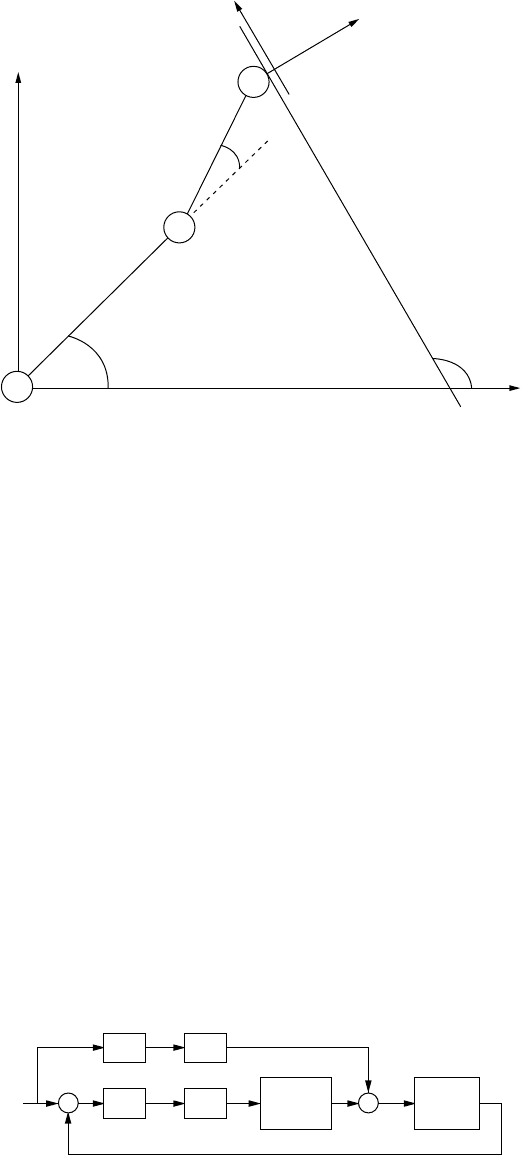
FIGURE 18.1 Rigid-link rigid-joint robot interacting with a constrain surface.

therefore either a position tracking problem in the q-state space or a force control problem or a hybrid of

both.

Example 18.1

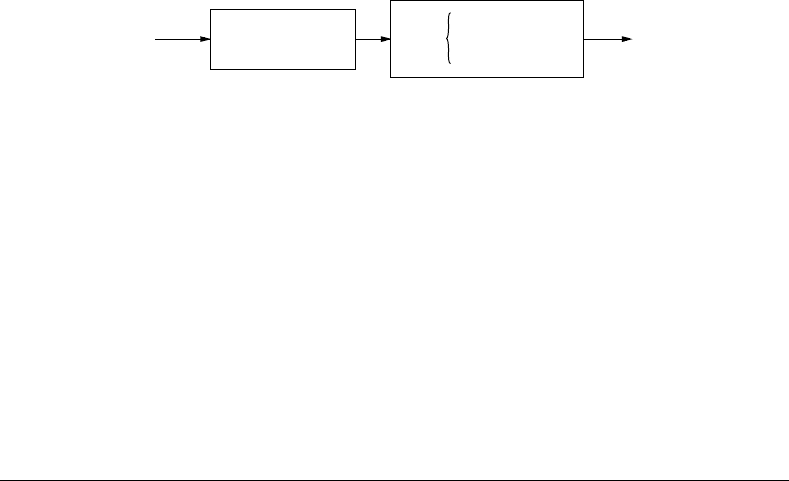
Consider the force control problem of the two-link robot depicted in Figure 18.1 [7]. A control scheme to

track a desired contact force F

is shown in Figure 18.2, where J

is the robot’s Jacobian matrix relative to

the coordinate system ﬁxed at the point of contact x

, y

, T is the n × n diagonal selection matrix with

elements equal to zero in the force controlled directions, F is the measured contact force, τ

is the output

of the feed-forward controller, and τ

the output of the sliding mode controller (Figure 18.2).

The matrices used to estimate the torque vector are

H(q) =



+ m

+ 2m

+ J

+ m

+ J



(18.8)

c(q,

q) =



−m

− 2m



(18.9)

I-T J

force

controller

robot and

constrain

surface

I-T J

–

FIGURE 18.2 Force controller with feed-forward compensation.

-4 Robotics and Automation Handbook

= s

+ k

∫

max

≥ 0

-s

max

< 0

sliding surface switching control law

FIGURE 18.3 Sliding mode force controller.

g(q) =



g(m

+ m



(18.10)

(q) =



−r



(18.11)

where C

= cos(q

), C

= cos(q

), S

= sin(q

), S

= sin(q

A similar compensation scheme can be used to solve the position tracking problem.

18.3 Equivalent Control and Chatter Free Sliding Control

Sliding mode control comprises two synergistic actions: reaching the sliding surface and letting the state

vector ride on it. These are represented as two different components of the control action: a switching term

) and a so-called equivalent control (u

). The robustness of sliding control is given by the switching

term, u

, derived from the sliding condition (18.4). This term takes the system from its arbitrary set

of initial conditions to the sliding surface and accommodates parametric uncertainties and unmodelled

dynamics by virtue of the switching action [3, 4, 5]. A purely switching controller can only provide high

performance at the expense of very fast switching. While in theory inﬁnitely fast switching can provide

asymptotically perfect tracking, in practice it implies a trade-off between tracking performance and control

signal chatter, which is either undesirable due to noise considerations or impossible to achieve with real

actuators.

After sliding has been achieved, the system dynamics match that of the sliding surface. Equivalent

control (u

) is the control action that drives the system once sliding has been achieved and is calculated

from solving dS/dt = 0. It is a nonrobust control law because it assumes the plant model to be exact, but

does not generate control chatter because it is a continuous function [5]. In systems that are afﬁne in the

input, such as the one described by Equation (18.1), both actions can be combined into a single control

law (u = u

), and several possible switching terms can be derived by forcing the compound control,

u, to satisfy the sliding condition [5]. An equivalent control term improves tracking performance while

reducing chatter, alleviating the performance trade-off implied by the switching gain k(x, t) in (18.5).

Several different methods have been proposed to deal with control chatter. Two basic approaches can

be distinguished.

1. The boundary layer method, which essentially consists of switching the control action in ﬁnite time

as the system’s trajectory reaches an ε-vicinity of the sliding surface.

2. The equivalent control method, which consists of ﬁnding a continuous function that satisﬁes the

sliding condition (18.4). This is particularly important in systems where the control action is

continuous in nature, such as motion control systems where torque, force, or current are treated

as the control input.

A boundary layer [3, 5] is deﬁned as

(t) ={x, s (x, t)|≤} (18.12)