Курбацкий А.Ф. Лекции по турбулентности. Часть 1

Соотношение (3.13) позволяет выразить трудно измеряемые в турбулент-

ном потоке пульсации плотности через легко измеримые пульсации темпе-

ратуры.

3.2. Уравнение переноса турбулентных напряжений

Для вывода точного незамкнутого уравнения переноса турбулентных

напряжений запишем определяющее полевое уравнение для турбулентной

флуктуации скорости в наиболее общем виде, включив в правую часть

уравнения (2.26) флуктуирующую силу плавучести:

,)/(

1

30

2

0

i

j

ji

i

ij

i

j

i

j

i

j

i

g

x

u

x

p

x

U

u

x

u

x

u

U

t

u

δρρ

τ

ν

ρ

−

∂

+∇+

+

∂

⋅−

∂

⋅−

∂

⋅−=

∂

⋅+

∂

(3.14)

где

−

0

ρ

постоянное (среднее) значение плотности, соответствующее не-

которому постоянному среднему значению температуры

,

0

T

−

p

турбу-

лентная пульсация давления, а

−

ρ

турбулентная пульсация плотности.

Уравнение (3.14) записано в приближении Буссинеска.

Если записать уравнение (3.14) в операторной форме

L = 0,

i

u

тогда уравнение переноса напряжений Рейнольдса получается из момента

второго порядка

i

u

<

L

jj

uu

+

L

0

=

>

i

u

(3.15)

в следующем явном виде:

.)()/(

1

330

2

0

jiij

k

j

i

k

i

j

i

j

k

kji

k

i

kj

k

j

ki

k

ji

k

ji

uug

x

u

x

u

x

p

u

x

p

u

x

C

x

U

x

U

x

U

t

δρδρρ

ν

ρ

ττ

><+><⋅−

−

⎟

⎠

⎞

⎜

⎝

⎛

>

∂

<+>

∂

<⋅+

⎟

⎠

⎞

⎜

⎝

⎛

>

∂

⋅<+>

∂

⋅<−

−

∂

−

∂

⋅−

∂

⋅−=

∂

⋅+

∂

(3.16)

С учетом следующих тождеств

71

,2

2

>

∂

<⋅+>

∂

⋅<+>

∂

⋅<≡

∂⋅∂

><∂

k

j

k

i

k

j

i

k

i

j

kk

ji

x

u

x

u

x

u

x

u

xx

uu

,>

∂

⋅<−>⋅<

∂

=>

∂

<

j

i

jj

i

x

u

pup

xx

p

u

>

∂

⋅<−>⋅<

∂

=>

∂

⋅<

i

j

ii

j

x

u

pup

xx

p

u

уравнение (3.16) преобразуется к окончательному виду

,)(

33

2

jiijjiji

ji

k

kji

k

i

kj

k

j

ki

k

ji

k

ji

uug

П

x

C

x

U

x

U

x

U

t

δθδθβτνε

ττ

τ

><+><⋅⋅+∇⋅−−

−+

∂

−

∂

⋅−

∂

⋅−=

∂

⋅+

∂

(3.17)

где

−><+><+><≡ )(

1

0

kijkjikjikji

pupuuuuC

δδ

ρ

турбулентная диф-

фузия,

>

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

∂

≡<

i

j

i

ji

x

u

x

up

П

0

ρ

− корреляция давление – сдвиг скорости,

−>

∂

⋅

∂

<⋅≡

k

j

k

i

ji

x

u

x

u

νε

2

тензор скорости диссипации.

В уравнении (3.17) слагаемое с флуктуирующей силой плавучести (по-

следнее слагаемое в правой части) записано согласно (3.13) через легко

измеримую корреляцию – вектор турбулентного потока тепла

>

<

−

i

u

θ

(

−

θ

турбулентная пульсация температуры).

Это уравнение, как и следовало ожидать, незамкнуто: помимо

одноточечных моментов поля скорости третьего порядка

в правой

части (3.17) имеется корреляция между пульсацией давления и градиентом

пульсационной скорости

, которая содержит двухточечные

корреляции поля скорости (см. «Лекции…», часть 2), а также тензор

kji

C

ji

П

72

поля скорости (см. «Лекции…», часть 2), а также тензор скорости вязкой

диссипации

ji

ε

.

Положив в уравнении (3.17) равными индексы,

ji

=

(суммирование по

повторяющимся индексам не проводится!), получим уравнение для плот-

ности (на единицу массы) компонент кинетической энергии турбулентости

:

><= uuE )2/1(

iii

3

2

1

iiiii

ii

k

kii

k

i

ki

k

i

k

i

ugE

П

x

C

x

U

x

E

U

t

E

δθβνε

τ

><⋅⋅+∇⋅−−

−+

∂

−

∂

⋅−=

∂

⋅+

∂

. (3.18)

3.3. Уравнение кинетической энергии турбулентности и

его следствия.

Уравнение для энергии турбулентности может быть

получено из уравнения (3.17) путем операции свертки (суммирования по

индексам

) :

><=

2

)2/1(

i

uE

ji =

,

)

2

11

(

2

0

EG

uuuup

x

P

x

E

U

t

E

jiij

j

E

j

∇++

+><+><−−=+

ν

ρ∂

∂

ε

∂

(3.19)

где

−

∂

⋅−≡

j

i

jiE

x

U

P

τ

генерация энергии турбулентности сдвигом скорости,

−>

∂

⋅

∂

<≡

j

i

j

i

x

u

x

u

νε

скорость диссипации энергии турбулентности,

−

>⋅<⋅⋅=

3

ugG

θ

β

генерация энергии турбулентности плавучестью.

Для последующего анализа удобно представить уравнение (3.19) в не-

сколько ином виде, опустив при этом и слагаемое

G

:

jjiij

jj

EE 1 1

U ( pu uuu us )

txx 2

∂∂∂

+ = − < >+ < >−ν< >

∂∂∂ρ

iij

73

>

⋅

<

−

>

<

−

jijijiji

ssSuu

ν

2

, (3.20)

где

)(

2

1

i

j

i

ji

x

U

x

U

S

∂

+

∂

=

− средний тензор скорости деформации, а

)//()2/1(

ijjiji

xuxus

∂

+

∂∂=

− турбулентная пульсация тензора ско-

рости деформации.

Как показывает уравнение (3.20), скорость изменения энергии турбу-

лентности

E

обусловлена процессами турбулентной диффузии (первый

член в правой части (3.20)) и двумя членами

jijiE

SuuP >

<

−

≡

и

><≡

jiji

ss

ν

ε

2

, определяющими работу деформации.

Турбулентная диффузия представляет собой «дивергенцию» потока

энергии. Следовательно, если поток энергии через поверхность контроль-

ного объема равен нулю, турбулентная диффузия может только перерас-

пределять энергию внутри контрольного объема, не изменяя её величины.

Члены, описывающие работу деформации, непосредственно влияют на

изменение величины кинетической энергии турбулентности. Генерация

энергии турбулентности

jiji

Suu >

<

−

− величина обычно положитель-

ная, потому что при

∂

Ux

ij

/ > 0

турбулентные напряжения

><−

ji

uu

ρ

оказываются положительными (сама корреляция

>

<

ji

uu

ве-

личина обычно отрицательная). Член генерации энергии турбулентности

сдвигом скорости в уравнении (3.20) отражает потерю энергии средним

течением и приобретение её полем турбулентности. Последний член в пра-

вой части (3.20) определяет скорость, с которой вязкие напряжения осуще-

ствляют работу деформации против флуктуирующей скорости деформа-

ции. Очевидно, что этот член представляет собой «потерю» энергии

турбу-

лентности (так как он квадратичен по

) и имеет, следовательно, физиче-

ский смысл вязкой диссипации кинетической энергии турбулентности,

непрерывно переходящий в энергию молекулярного движения сплошной

среды.

s

ij

3.3.1. Локально-равновесная турбулентность.

В установившемся однородном течении чистого сдвига, в котором все

осредненные величины, исключая среднюю скорость

, не зависят от

местоположения в пространстве и в котором

является константой,

уравнение (3.20) принимает особенно простой вид

U

i

S

ij

74

>⋅

<

=

>

<

−

jijijiji

ssSuu

ν

2 . (3.21)

Это уравнение устанавливает, что в таком течении скорость генерации

энергии турбулентности равна скорости вязкой диссипации. Можно заме-

тить, что в большинстве течений порождение и диссипация не балансиру-

ются, хотя они и близки всегда по порядку своей величины. Учитывая это,

можно использовать (3.21) как средство для понимания тех свойств турбу-

лентности, которые

прямо не связаны с пространственным переносом.

Удобно (3.21) записать в символической форме

ε

=

E

P

. (3.22)

Для того чтобы выяснить смысл равенства (3.22), можно использовать

оценки

и , предполагая, что сдвиговая турбу-

лентность имеет один характерный масштаб скорости и один характерный

линейный масштаб. Оценивая генерацию турбулентности как

LuS

ji

/

ˆ

∝

2

ˆ

uuu

ji

∝><−

=

>

<

−

jiji

Suu

jiji

SSLuc ⋅

⋅

ˆ

0

,

баланс энергии турбулентности (3.22) можно записать в виде

culS S s s

ij ij ij ij0

2

⋅

=

<

⋅

>



ν

, (3.23)

где

− численный коэффициент порядка единицы.

0

c

Для чисел Рейнольдса

1/)

ˆ

( >>

⋅

ν

Lu

из (3.23) следует, что

jijijiji

SSss >>

<

. (3.24)

Флуктуирующая скорость деформации

, таким образом, много больше,

чем средняя скорость деформации

, когда число Рейнольдса велико.Так

как скорость деформации имеет размерность

, вихри, вносящие наи-

больший вклад в диссипацию энергии, имеют, следовательно, малый вре-

менной масштаб по сравнению с временным масштабом среднего течения.

Это наводит на мысль, что должно быть весьма малое прямое взаимодей-

ствие между флуктуациями скорости деформации и средним течением,

если число Рейнольдса велико. Другими словами,

и сильно не

взаимодействуют, потому что они не настроены на одну и ту же полосу

частот; взаимодействие слабое, оно не носит резонансного характера. По-

этому мелкомасштабная структура турбулентности проявляет тенденцию

быть независимой от любых эффектов ориентации, вносимых средним

сдвигом, так что все осредненные характеристики малых вихрей не изме-

няются при вращениях

и зеркальных отражениях системы координат. Если

s

ij

S

ij

c

−1

S

ij

s

ij

75

это имеет место, то мелкомасштабную структуру называют изотропной.

Изотропность на малых масштабах называется локальной изотропией.

3.3.2. Тейлоровский микромасштаб турбулентности.

Предшествующие р смотрения предполагали, что любой пр транст-

венный масштаб, входящий в оценку

s

ij

, должен ть много меньше, чем

интегральный масштаб турбулентности

L , если имеет есто баланс между

генерацией и диссипацией. Подобная ситуация возникает и в теории лами-

нарного пограничного слоя. В ламинарных пограничных слоях толщина

слоя

ас ос

бы

м

δ

опреде яется условием, чтобы существенный вязкий член в урав-

нении движения мог быть сохранен; это дает:

δ

/l ≈

л

−12

.

>

1

2

Re

/

Введем в рассмотрение новый микромасштаб турбулентности. Дисси-

пация энергии пропорциональна ковариации

, которая включает

члены, подобные

, большинство из которых обычно не

может быть измерено в опыте. Однако, как выше было замечено, мелко-

масштабная структура турбулентности стремится к изотропии. В изотроп-

ной турбулентности скорость диссипации энергии равна:

<ss

ij ij

<(/ )

∂∂

ux

ij

2

. (3.25)

εν ν∂∂

≡< >=⋅<215

11

2

ss u x

ij ij

(/)

(Вывод этого выражения здесь не приводится. Его можно найти в книге

О.Хинце [2]). Коэффициент

15 в (3.25) значительно больше единицы, так

как учтено много составляющих компонент в ковариации. В любом тече-

нии величина

может быть относительно легко

<(/)

∂∂

ux

1

измерена.

Теперь может быть введен в рассмотрение новый линейный масштаб

. (3.26)

<>≡<>=(/) /



/

∂∂ λ λ

ux u u

11

2

1

222

Линейный масштаб

λ

называется тэйлоровским микромасштабом в честь

Дж. Тейлора, который первым ввел в теорию турбулентности соотношение

(3.26). Замена

может быть сделана потому, что в изотропной

турбулентности

, так что , которая опреде-

ляется как

<>=u

1

2



u

2

><>=<>=<uuu

1

2

3

2



u

2

(/)13

<

>uu

ii

, равна . Так как мелкомасштабная

структура турбулентности при больших числах

всегда приближенно

изотропна, можно использовать для скорости диссипации в качестве под-

ходящей оценки представление вида

<u

1

2

>

Re

76

(3.27)

εν

=⋅15

2



/u

λ

2

с линейным масштабом

λ

, определяемым выражением (3.26).

Соотношение между масштабами

λ

и может быть получено из про-

стого выражения (3.21) баланса энергии. Если

− величина

L

S

ij

Lu /

ˆ

∝

и

если

, тогда

2

ˆ

uuu

ji

∝><−

. (3.28)

223

/

ˆ

15/

ˆ

λν

uLuA ⋅⋅=⋅

Отношение

L/

λ

тогда равно:

2/1

2/12/12/1

Re

15

ˆ

15

−

⋅

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

=

L

A

Lu

AL

ν

λ

. (3.29)

В (3.28) и (3.29) величина

− неопределенная константа, которая пред-

положительно равна единице (см. рис. 8 и 9). Так как во всех турбулентных

течениях

, тейлоровский микромасштаб

A

1Re >>

L

λ

всегда много меньше

интегрального масштаба турбулентности

. Это опять-таки свидетельству-

ет о том, что диссипация энергии турбулентности происходит в мелких

вихрях.

L

Отношения масштабов. Тэйлоровский микромасштаб не наименьший

из масштабов турбулентности. Наименьший масштаб турбулентности –

колмогоровский микромасштаб

, (3.30)

4/13

)/(

ενη

=

введенный в п. 1.4.2.

Различие между масштабами

λ

и

η

можно установить, если обратить-

ся к определению скорости диссипации энергии турбулентности

>⋅

<

≡

jiji

ss

ν

ε

2

(3.31)

в уравнении (3.20) и её оценке (3.27).

Флуктуация скорости деформации

имеет размерность частоты ,

и формула (3.31) дает масштаб времени, связанный с диссипативной струк-

турой турбулентности:

ji

s

1−

c

. (3.32)

2/1

)/(

εντ

=

Этот временной масштаб идентичен тому, который был введен в п. 1.4.2 по

существу из соображений размерности. Такое совпадение не случайно.

77

Размерность

такова, что тэйлоровский микромасштаб

ji

s

λ

был опреде-

лен через масштаб скорости

. Вообще говоря, для такого выбора харак-

терной скорости нет физических оснований. Масштаб, который может

быть введен в рассмотрение недвусмысленно,

− это временной масштаб

u

ˆ

τ

.

Тэйлоровский микромасштаб следует использовать только в сочетании,

следующем из его определения (3.27):

. (3.33)

2/11

)/(26,026,0/

ˆ

νετλ

⋅=⋅=

−

u

Тэйлоровский микромасштаб не представляет собой характерный ли-

нейный масштаб поля скорости деформации и не соответствует характер-

ному масштабу группы вихрей, в которой сильны диссипативные эффекты.

Это не диссипативный масштаб, потому что он определяется с помощью

масштаба скорости, который не связан с диссипативными вихрями. Тем не

менее тэйлоровский масштаб широко используется

потому, что оценка

λ

/

ˆ

us

ji

∝

просто удобна: микромасштаб

λ

легко вычисляется по изме-

ренной эйлеровой корреляционной функции.

Чтобы убедиться в этом, рассмотрим, например, коэффициент корреля-

ции эйлеровой продольной корреляционной функции

>+⋅<

>

+

⋅

<

=

)()(

)(

11111

111

xuu

xR

ξξ

ξ

(3.34)

между продольными компонентами пульсационной скорости в двух точ-

ках, расположенных на линии параллельной оси

, с координатами

1

x

1

ξ

и

11

x+

ξ

, соответственно. Разложим функцию в ряд Тэйлора в окре-

стности нуля, ограничившись в этом разложении первым членом ряда:

)(

111

xR

>

⎥

⎦

⎤

⎢

⎣

⎡

∂

<⋅

><

⋅−≅

=

2

0

1

2

1

2

1

111

1

!2

1)(

x

u

x

xR

. (3.35)

Из разложения (3.35) следует, что при малых значениях

корреляция

имеет параболическую зависимость от координаты . В соответ-

ствии с определением (3.26) выражение (3.35) можно записать с введением

в него масштаба

1

x

)(

111

xR

1

x

λ

:

78

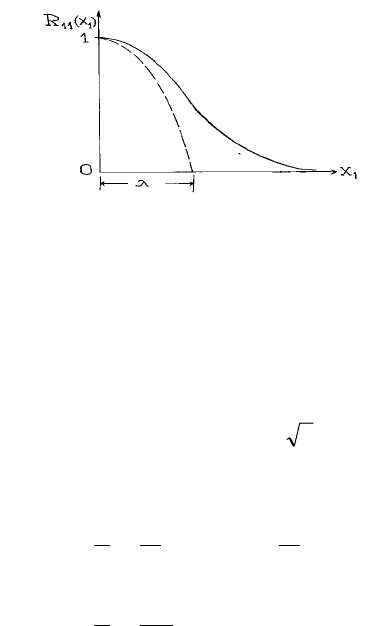
)/(1)(

22

1111

λ

xxR −≈

. (3.36)

Выражение (3.36) описывает параболу с вершиной в точке

0

1

=

x

, где она

соприкасается с кривой корреляционного коэффициента. П этому велио чи-

на

λ

отыски (рис. 20).

0. Пара продольной кор-

1

x

вается по пересечению этой параболы с осью

Рис. 2 бола, соприкасающаяся с кривой коэффициента

реляции

)(

111

xR

, и тэйлоровский микромасштаб турбулентности

λ

.

Отметим, что в выражение (3.37) входит продольный тэйлоровский мик-

ромасштаб

λ

, который в общем случае отличается от поперечного микро-

масштаб турбулентности, определяемого по поперечной эйлеровой

корреляционной функции. В случае и ропной турбулентности

про

зот

дольный тэйлоровский микромасштаб в

2 раз больше поперечного

штаба. микромас

Для дальнейшего полезно выписать следующие отношения масштабов:

12/1

2/1

1515

−−

⋅=⋅

⎟

⎠

⎞

⎜

⎝

⎛

=

λ

eR

A

eR

AL

L

, (3.37)

2/14/14/1

4/1

15

225

λ

η

L

⎠⎝

Неопределенная постоянная

A та же самая, что и в выражении (3.28) и

(3.29). Параметр

eR назыв

λ

eReR

A

⋅=

⎟

⎞

⎜

⎛

=

. (3.38)

микромасшт и

λ

ает абным числом Рейнольдса

опр

ся

еделяется выражением

νλ

λ

/)

ˆ

( ⋅= ueR . (3.39)

79

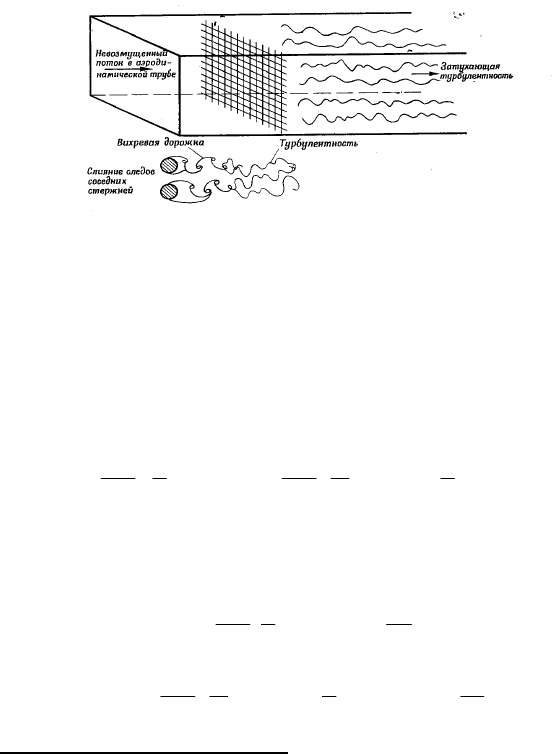
Затухание однородной турбулентности. В качестве приложения урав-

нения баланса кинетической энергии турбулентности (3.19) рассмотрим

задачу о затухании приближенно однородной турбулентности за решеткой

(в низкоскоростной аэродинамической трубе), на которую набегает одно-

родный поток без сдвига средней скорости (рис. 21).

Рис. 21. Схема течения в аэродинамической трубе и картина слияния следов с

образованием однородной турбулентности вниз по потоку от решетки

*

.

д ер служит указанием на то, что приближе-

ние

Если

0=

ij

S

, генерация энергии турбулентности сдвигом скорости от-

сутствует; турбулентность в такой ситуации будет затухать вследствие

вязкой ипации. Этот примисс

P ≈

ε

не всегда уместно.

В системе отсчета, в которой

1

U

- единственная отличная от нуля ком-

понента средней скорости течения, уравнение баланса энергии турбулент-

ности (3.19) принимает вид

ε

ρ∂∂

⎟

⎠

⎜

⎝

⎠⎝

1

11

1

22 xx

i

Уравнение (3.40) записано в предположении, что

1>>

L

eR и член вязкой

диффузии энергии в этом уравнении не учитывае

∂∂

−

⎟

⎞

⎜

⎛

><+><−=

⎟

⎞

⎜

⎛

><

1

2

111

uupuuU

i

. (3.40)

тся как пренебрежимо

малый. Оценим порядки величин этого уравнения:

⎟

⎠

⎞

⎜

⎝

⎛

⋅∝

⎟

⎠

⎞

⎜

⎝

⎛

><⋅

2

1

2

1

ˆ

2

1

u

x

U

u

x

U

i

∂

,

⎟

⎠

⎞

⎜

⎝

⎛

∝

⎟

⎠

⎞

⎜

⎝

⎛

><+><−

1

3

1

2

1

ˆ

2

11

x

u

uuu

x

i

ρ

ρ∂

∂

, (3.41)

*

Воспроизведено по кн.: Брэдшоу П. Введение в турбулентность и её измерение.

М.: Мир, 1974.

80

Курбацкий А.Ф. Лекции по турбулентности. Часть 1

Подождите немного. Документ загружается.