Курбацкий А.Ф. Лекции по турбулентности. Часть 1
Подождите немного. Документ загружается.


=
′
∫
′′
−
∫
′
=
∫∫
′
′′
tdttdtdtd
t
L
t
t
L
tt
L
0
0
000
)()()(
ρττρττρ
ττρτττρ
ddt
t
L
t
L
)()(
00
∫∫
−=
преобразует (1.37) к виду
.)()(2)(
0
2
2
2
2
∫
−><=
t
L
dtvtX
ττρτ
(1.38)
Формулы (1.36) и (1.38) определяют зависимости дисперсии смещения
жидкой частицы вследствие турбулентных пульсаций скорости от лагран-
жевой корреляционной функции
.
)()(
2
2
τρτ
LL
vR ><=
Особенно важен характер этой зависимости при больших значениях
.
Согласно опытным данным лагранжевый коэффициент корреляции
t
0)( →
τ
ρ
L
при
.
∞
→
τ
В таком случае интеграл в правой части (1.37)
при больших
мало отличается от постоянной величины, называемой ла-
гранжевым интегральным масштабом времени:
t
(1.39)
∫
=
∞
0
.)(
ττρ
dT
LL
Отметим, что уже при значении
L
T⋅>3
τ
выполняется неравенство
01,0<
L
ρ
; следовательно, интеграл (1.39) быстро стремится к своему
асимптотическому значению.
Для моментов времени
L
T>>
τ
скорость дисперсии смещения части-
цы, определяемая формулой (1.36), может быть представлена в виде произ-
ведения дисперсии скорости частицы на лагранжевый интегральный мас-
штаб времени:
.)(
2
1
2
2
0
2
2
2
2 LLt
TvdvX
dt
d
⋅><
∫
=><=
⎟
⎠
⎞
⎜
⎝
⎛
><
∞
∞→
ττρ
(1.40)
При больших значениях времени
выражение (1.38) можно предста-
вить в виде
t
31

,)(
2
0
2
2
2
2
2
2
LL
t
T
Tvdv
t
X
D ⋅><=><=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
><
≡
∫
∞
∞→
ττρ
(1.41)
где
− коэффициент вихревой (или турбулентной) диффузии. Этот же
результат получается интегрированием приближенной формулы (1.40) по
времени.
T
D
Выражения (1.40) и (1.41) представляют собой параболический закон
диффузии в поле однородной турбулентности. Согласно (1.41) дисперсия
смещения частицы за достаточно большой промежуток времени
пропор-
циональна величине
, что аналогично закону броуновского движения.
t
t
Интегральные масштабы турбулентности. Лагранжевый интеграль-
ный масштаб времени
трудно определить экспериментально, так как
для этого требуется проследить за движением очень большого числа жид-
ких частиц, как-либо помеченных: фотографическим путем или с помощью
метода радиоактивных трассеров.
L
T
В практике исследования турбулентности используются главным обра-
зом эйлеровые корреляции гидродинамических полей, поскольку измере-
ния обычно проводятся в фиксированных точках лабораторной системы
отсчета. Связь между лагранжевыми и эйлеровыми корреляциями доволь-
но трудно установить, особенно для неоднородных турбулентных течений.
Однако, к счастью, в большинстве турбулентных течений лагранжевые
интегральные масштабы (длины и времени) оказываются сравнимыми по
порядку величины с эйлеровыми интегральными масштабами длины и
времени.
Эйлеровый линейный интегральный масштаб турбулентности опреде-
ляется с помощью двухточечной
корреляции турбулентного поля скорости.
Пусть две точки имеют координаты
и ),,( zух
),,(
321
rzryrx
+
+
+
или, в векторной форме,
x
G
и .rx
G
G
+
Тогда ковариация продольной компо-
ненты турбулентной скорости определяется как
>+⋅< )()( rxuxu
G
G
G
(в общем
случае она зависит от
x
G
и
r
G
). Обычно из соображений удобства исполь-
зуется безразмерная величина
><
>
+
<
=
)(
)()(
),,(
2
32111
xu
rxuxu
rrrR
G
G
G
G
,
32
а для корреляций компонент флуктуаций скорости
и используют
обозначения
и Измерение корреляций для всевозможных векто-
ров
v w
22
R .
33
R
r
G
и последующая обработка представляли бы собой «сизифов труд».
Поэтому обычно измеряются корреляции для точек, лежащих на отрезке,
параллельном одной из осей координат. Например, − корреля-
ция поперечной компоненты скорости для точек, расположенных на пря-
мой, параллельной оси
)0,0,(
122
rR
x
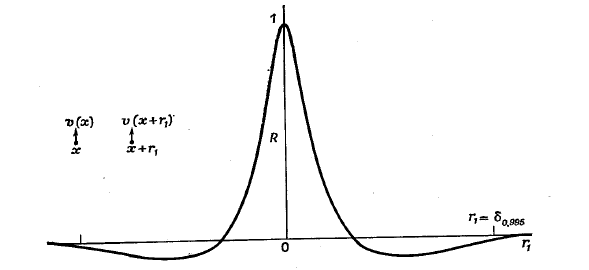
, с интервалом (рис. 13).
1
r
Рис. 13. Типичная корреляционная функция пограничного слоя
при
)0,0,(
122
rR
⋅><>+<== )(/)()()0,0,(.5,0/
2
1122995.0
xvrxvxvrRy
δ
Физически корреляция для точек, разделенных расстоянием
r
, дает меру
интенсивности вихрей, размер которых в направлении вектора
r
G
больше
абсолютной величины
r
(так как более мелкие вихри не вносят вклада в
корреляцию). Такая интерпретация, правда, не вполне точна, поскольку
корреляции для трех компонент скорости различны при одном и том же
r
G
в силу анизотропного характера турбулентности в общем случае. По этой
причине интегральные масштабы турбулентности, определяемые как
, (1.42)
)3,2,1(,)(
0
==
∫
∞
idrrRL
iiiiii
оказываются, вообще говоря, различными в разных направлениях в случае
неоднородной турбулентности. Таким образом, введенная в разд. 1.4 вели-
чина линейного размера энергосодержащих вихрей, определяется согласно
(1.42) по измеренной двухточечной корреляционной функции турбулент-
33

ного поля скорости
),( txu
G
G
и называется обычно интегральным масшта-
бом турбулентности.
Спектр и перенос примеси турбулентными вихрями. К установлен-
ному в п. 1.4.1. одному из самых важных положений современной теории
турбулентности (1.28) можно придти, рассматривая спектр корреляции
R
L
()
τ
.
Спектр есть преобразование Фурье корреляционной функции. Посколь-
ку функция
ρ
τ
L
()
− вещественная и симметричная функция со значением
ρ
= 1 в начале координат, то ее преобразование Фурье должно быть не-
прерывной, симметричной, положительной и вещественной функцией
, (1.43)
ωωτωτ
dER
LL
⋅=
∫
∞
cos)()(
0
τωττ
π
ω
dRE
LL
⋅=
∫
∞
cos)(
2
)(
0
. (1.44)
Функция
E
L
()
ω
называется энергетическим спектром, поскольку
Ed
L
()
ω
ω
характеризует вклад в суммарную дисперсию возмущений в
интервале частот от
ω
ω
−
d /2
до
ω
ω
+
d /2
. При
τ
=
0 из (1.43) сле-
дует, что
. (1.45)
ωω
dEvR
LL
)()0(
0
2
2
∫
∞
=><=
Из (1.45) следует, что проинтегрированный по всему диапазону частотный
спектр дает удвоенное значение кинетической энергии. При значении
ω
=0 из (1.44) получается
LLL
TvdRE ⋅><=⋅=
∫
∞
2
2
0
2
)(
2
)0(
π
ττ
π
, (1.46)
откуда следует, что значение спектра при значении
ω
=
0 определяет ко-
эффициент турбулентной диффузии.
Описание динамики мелкомасштабной структуры турбулентности
можно получить, рассматривая эволюцию вихрей, рассеивающих примесь.
Для этого оценим сначала вклад возмущений различных частот в суммар-
ную дисперсию частицы примеси. Общее выражение (1.38) для дисперсии
34
><
2
2
2/1 X
можно записать в преобразованном виде, если воспользовать-
ся теоремой Парсеваля, согласно которой свертка корреляционной функ-
ции
R
L
()
τ
с треугольным фильтром
(/1 )
−
τ
t
равна интегралу от пре-
образования Фурье
E
L
()
ω
функции
R
L
()
τ
, умноженному на преобра-
зование Фурье-фильтра:
ω
ω
ω
ωτττ
d
t
t
EtdRtX
LL
2
0
2
0
2
2
2/
2/sin
)(
2
1
)()(
2
1
⎥
⎦
⎤
⎢
⎣
⎡
⋅=−=><
∫∫
∞∞
. (1.47)
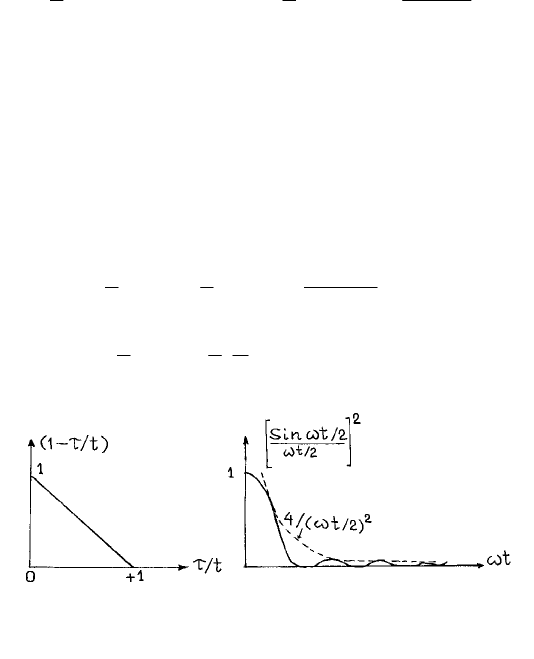
Главная полоса пропускания фильтра в (1.47) расположена вблизи
ω
=
0
(боковые «окна» в области высоких частот не играют большой роли и мо-
гут не рассматриваться; см. рис. 14).
Фильтр при очень больших значениях времени
становится узким, по-
скольку первые нулевые значения фильтра достигаются при
t
ω
π
=
2/t
. В
подынтегральном выражении (1.47) существенно лишь значение
E
L
()
ω
при близких к нулю
ω
и практически исключается вклад возмущений бо-
лее высоких частот. Интеграл (1.47) представляется приближенно в виде
=
⎥
⎦
⎤
⎢
⎣
⎡
=><
∫
∞
ω
ω
ω
d
t
t
EtX
L
0
2
22
2
2/
2/cos
)0(
2
1
2
1
tTv
t
Et
LL
⋅⋅><=⋅⋅=
2
2
2
2
2
)0(
2
1
π
. (1.48)
Рис. 14. Треугольный фильтр и его Фурье-образ.
При записи (1.48) использовано значение спектра в нуле согласно (1.46).
Можно сделать вывод, что диффузия за длительное время
определяется
t
35

характером спектра в области самых низких частот.
При очень малом значении времени
первое обращение в нуль подын-
тегрального выражения происходит при очень высоких частотах. Посколь-
ку численное значение фильтра при
t
0
=
ω
равно единице, первое прибли-
жение (1.47) при
tT
L
<
<
может быть записано в виде
22
2
0
22
2
2
1
)(
2
1
2
1
tvdEtX
L
⋅><==><
∫
∞
ωω
, (1.49)
и, следовательно, возмущения всех частот в выражение общей дисперсии
входят с одинаковым весом.
><
2
2
X
После выпуска примеси из источника рассеяние частиц турбулентными
пульсациями скорости в течение очень короткого интервала времени опи-
сывается выражением (1.49), в котором никак не отражено влияние эволю-
ции турбулентности; начальная фаза такого рассеяния определяется пуль-
сациями скорости у источника в момент выброса примеси.
Чтобы учесть эволюцию вихрей,
рассеивающих примесь, формула
(1.49) должна быть модифицирована. Из (1.47) следует, что с ростом
фильтр, описывающий процесс осреднения становится все уже и все боль-
ше ослабляется влияние высокочастотных возмущений скорости. Это оз-
начает, что первая поправка к (1.49) должна быть отрицательной: рассея-
ние замедляется по сравнению с его начальной стадией. Приведенный вы-
ше анализ спектра также означает, что указанная поправка должна быть
связана с динамикой
высокочастотных возмущений (мелкомасштабных
вихрей).
t
Возьмем коэффициент корреляции в приближенной форме
(1.50)
.)(
/
L
T
L
e
τ
τρ
−
=
Выражение (1.50) неплохо аппроксимирует значение коэффициента корре-
ляции, полученное в измерениях, и обладает всеми достоинствами анали-
тической функции с незначительным недостатком (определенная при
0>
τ
функция
)(
τ
ρ
L
недифференцируема в нуле, так как она должна
быть четной функцией
τ
). Тогда (1.38) запишется в виде
}]1{[
2
1
/
22
2
2
2
L
Tt
LL
eTtTvX
−
−−><=><
.
(1.51)
Пред
/
ставим (1.51) в виде ряда по степеням малого параметра
tT
<
< 1
:
L
36

]
3
1
1[
11
222
"+−><=>
t
tvX
. (1.52)
2
22
L
T
отрение так называемую лагран
0202
()(()(
τ
tvtvD
L
ачениях
2
<
Введем теперь в рассм жевую структурную
функцию скорости
>
2
))
τ
,
+−<=
связанную с корреляционной функцией соотношением
)(22)(
2
2
ττ
LL
RvD −><=
. (1.53)
См
τ
ысл введения структурной функции в том, что при малых зн
она частотные
дставляя (1.43) и (1.45) в (1.53), н
)(
ωω
d
.
При
представляет собой фильтр, эффективно обрезающий низко
возмущения.
Действительно, по аходим
∫
−=
0
)cos1(2)(
τωτ
ED
LL
(1.54)
∞
τ
<< T
L
пе максрвый имум множителя (cos )1
−
ω
τ
расположен в
высокочастотной области энергетического спектра
E
().
ω
По
(cos )10−=
скольку
ω
τ
при 0
=
ω
, то наиболее крупномасштабные возмущения
вообще не вносят вкл значение интегра
()
ада в ла (1.54) и функция
D
τ
L
целиком определяется только мелкомасштабными возмущениями (при ус-
ловии, конечно, что
τ
/ T
L
<
< 1
).
Теория инерционного интервала в спектре турбулентности основывает-
ся на гипотезе Колмогорова (более подробно эта теория излагается в разд.
3.7 и во 2-й части «Лекций…»). Гипотеза утверждает, что статистические
характеристики мелкомасштабной турбулентности в той части спек-
тра, на которую не оказывают влия молекулярная зкость и крупно-
ма
ния вя
тольк
и кине-
ти
сштабные возмущения, зависят о от
скорости диссипаци
ческой энергии турбулентности
ε
и мых пере- от значений независи
менных.
Следовательно, при значении
tT
L
<
<
структурная функция
),()(
τ
ε
τ
fD
L
=
г х ри не зависит ни от каких д ов.
Принимая во внимание р ичин, получаем для структурной
ру и парамет
ци
азмерность вел
функ и выражение (А.М.Обухов, Л.Д.Ландау)
τ
ε
β
τ
⋅
=
)
L
D
(1.55)
(
,
37
где
β
−
инерционном интервале,
де − масштаб ипа-
неизвестная безразмерная постоянная. Выражение (1.55) −
лагранжевая структурная функция в
ετεν
/)/(
2/1
E<<<<
, г времени вязкой дисс
ции,
E
2/1
)/(
εν
/
ε
− инерционный масштаб времени. Соответствующее выраже-
ние для корреляционной функции имеет вид
τεβτ
1
)(
2
2
−><= vR
L
. (1.56)
2
в (1.56) со вторым членом в (1.5
интегрирование по
Сопоставим второй член 2). Для этого под-
τ
:
ставим (1.56) в общее выражение (1.38) и выполним
⋅⋅⋅+−⋅><=><
322
2
2
2
122
tX
εβ
. (1.57)
111
2
tv
Приравнивая правые части (1.57) и (1.52), находим
L
T
v ><
⋅=
2
2
2
β
ε
. (1.58)
Получен результат, установленный в разд. 1.4 из качественных сообра-
жений, а именно: скорость диссипации кине ической энергии турбулент-
ности определяется динамикой энергосодержащих вихрей. Лагранжевый
интегральный масш
т
таб
имеет смысл масштаба времени энергонесущих
змущений. В выра
T
L
во жении (1.58) величина
β
− неопределенный числен-
ный
ользуются урав-
нен ел
ощью декомпозиции (1.3) и
(1.6).
переменных
коэффициент.
2. Турбулентный перенос
2.1. Уравнения Рейнольдса для осредненного потока.
Турбулентные напряжения
Как отмечено в разд. 1.2, описание турбулентности во всех пространст-
венно-временных точках оказывается невозможным. Вместо этого, следуя
О.Рейнольдсу, для описания турбулентности обычно исп
ия для осредненных в ичин термогидродинамических полей. Эти
уравнения получаются из (1.1) – (1.2) с пом
последующего осреднения по ансамблю реализаций
φ
и
ψ
Для
любого течения принимаются следующие
пра е О.Рейнольдсом: вила, сформулированны
38

~
~
,0
=><
.0
,
=>⋅<=>Ψ⋅<
><+Ψ⋅
=
>
<
=
>
<
ψφ
φψψφ
ψ
φ
Ф
Ф
(2.1)
С учетом правил (2.1) осредненное «по Рейнольдсу» уравнение Навье −
кса (1.1) записываетсяСто в виде
2
1
,
ν
ρ
∂
<>
∂∂ ∂
+=− +∇−
∂∂ ∂
ij
ii
ji
uu
UU P
UU
tx
(2.2)
∂
j
x x
где
напр
турбулентных точечная
ji
−><
ji
uu
симметричный тензор яжений Рейнольдса или тензор
напряжений (одно корреляция турбулентного поля
скорости второго порядка).
Уравнение неразрывности
0=
∂
∂
i
i
x
U
(2.3)
получается как результат осреднения уравнения (1.2).
Физическая причина по ения в уравнении (2.2) н пряжений Рей-
нольдса обусловлена самовозбуждением поля скорост больших чис-
лах Рейнольдса. А сам факт присутствия в правой час нения (2.1)
дивергенции турбулентных напряжений означ
(2.
явл а
и при
ти урав
ает, что система уравнений
2) – (2.3) не образует замкнутой системы для определения искомых по-
лей средней скорости
),( txU
i
G
и среднего давления ),( txP
G
, потому что
корреляционный тензор турбулентного поля скорости
>
<
ji
uu
содержит
шесть дополнительных неизвестных величин.
Таким образом, как и для любой друго ейной физической систе-
мы, еский метод не приводит к замкнутому описанию динамики
турбулентности. В рамках статистического метода решени
зам
й нелин
статистич
е «проблемы
о
ыкания» в турбулентности заключается в том, чтобы установить физи-
чески к рректную связь между тензором
>
<
ji
uu
и средним полем скоро-
сти
универсального вида, если ожно. Смысл последней
ого ятным из дальнейшего
Мера степени корреляции между пульсационными компонентами ско-
),( txU
i
G
это возм
ворки станет более пон изложения.
рости
i
u
и
j
u характеризуется коэффициентом корреляции
39

><⋅><
><
=
22
ji
ji
ji
uu
uu
c
, (2.4)
где ие по повторяющимся индексам не проводится.
Если
1±=
ij
c
, то корреляция, как говорят, идеальная. Каждая переменная,
конечно, идеально коррелирует сама с собой: при
.1, ===
αα
α
cji Величи-
на
суммирован
><=
2
ˆ
ii
uu называется стандартным отклонением или среднеквадра-
тичной флуктуацией скорости. В п 1.4.1 отмечено, что масштаб скорости
турбулентных флуктуаций, например в ту
.
рбуле м слое,
мо и
i
u
ˆ
данном
но, при анализ
сл й
нтном погранично
жет быть определен как среднее значение скорост
попе-
речном сечении. Следователь е размерностей характерному
масштабу турбулентной скорости
u
ˆ
может быть дано точное определение
всякий раз, когда это бывает необходимо.
По едни член в правой части уравнения (2.2),
>
в
<
∂
∂
−
jij
uux/
, ана-
логичен адвективному члену
)(/
jij
UUx
∂
∂
. Он описывает средний пере-
нос флуктуирующего импульса турбулентными пульсациями скорости.
Если
i
u
и
j
u не коррелируют между собой, отсутствует и турбулентный
перенос импульса. Однако опытные данные показывают, что перенос тур-
булентного импульса есть основное свойство турбулентного движения и
последний член в правой части уравнения (2.2) не может быть равен нулю.
Средний перенос флуктуирующего импульса может импульс
сре
ен импульсом
изменять
днего течения, как это вытекает из уравнения (2.2). Последний
член в
правой части уравнения (2.2) описывает обм между турбу-
лентностью и средним течением, даже если средний импульс турбулент-
ных флуктуаций скорости и равен нулю;
0
=
><
i
u
ρ
.
Поскольку поток импульса связан с действующей силой вторым зако-
ном Ньютона, член турбулентного переноса
jji
xuu
∂
>
<
∂
/
можно пони-
мать как дивергенцию напряжения. Вследствие рейнольдсового разложе-
ния 3) турбулентное движение может восприниматься как воздействие,
ген ия в среднем течении Ввиду
этог (2.2) можно позво-
записать урав
(1.
ерирующее напряжен сплошной среды.
о все напряжения в уравнении собрать вместе, что
ляет нение Рейнольдса для среднего импульса в виде
40
