Курбацкий А.Ф. Лекции по турбулентности. Часть 1

,

1

j

ji

j

i

j

x

T

x

U

t ∂

∂

=

∂

+

∂

ρ

(2. 5)

где

∑

+=

ji

jiji

T

τ

− полный тензор апряжений в турбулентном потоке,

i

U

∂

н

∑

ji

S тензор напряжений осредненного движения −+⋅−=

ji

P

νρδ

2

сплошной среды,

>

<

−

=

jiji

uu

ρ

τ

− тензор турбулентных напряжений. (В

п. 2.

турб

3.1 на основании качественных соображений показано, что корреляция

улентного поля скорости

>

<

ji

uu

− величина отрицательная). Осред-

остей деформаций определяется вырненный тензор скор ажением

⋅

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

∂

=

j

i

ji

U

x

U

S

2

1

2.2. Линейные и временные масштабы молекулярного

и турбулентного движений

Нахождение связи между тензором рейнольдсовых напряжен й

i

x

и

ji

τ

и

средним тензором скоростей деформаций

ji

S (реологического уравнения

состояния «турбулентной жидкости») для получения замкнутой формы

уравнения Рейнольдса (2.2) и по сей день остается насущной задачей по-

строения теории турбулентности, хотя простейшие связи такого рода были

установлены еще Буссинеском (1877 г.). Функция напряжений Рейнольдса

равнении (2.5) кажется подобной функции вязких напряжений

ji

S

в у

ρ

ν

2

уравнении Навье − Стокса (1.1). Поэтому полезно вначале рассмотреть

простейшие феноменологические представления теории молекулярного

в

переноса в неплотном газе, для которого это можно сделать непосредст-

вен идкостей кинетическая

та столь же хорошо, как для газов.

нор

3

x

но. Для (капельных) ж теория и близко не разви-

Молекулярный перенос. Пусть имеется чисто сдвиговое течение, од-

одное в плоскости

)(

1

x

:

0;0)(

3

,

221

=

≠

UUxU

. Если течение

ламинарное, отличными от н ля компон нтам язких напряжений будут

у е и в

2

1

xd

Ud

⋅⋅==

νρσσ

. (2.6)

122

41

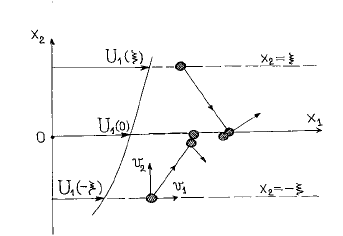
Напряжение сдвига

21

σ

есть результат молекулярного переноса им-

пульса в направлении оси

2

x

. Пусть

1

v

и

2

v

есть компоненты вектора

молекулярной скорости в р сматриваемом ламинарном течении чистого

сдвига в направлении

соответственно. Импульс

1

vm

молеку-

лы массы

m в направлении оси

1

x

переносится в направлении оси

2

x

,

если компонента скорости

коррелирует с компонентой скорости

ас

осей

и

Пе рцио л

лекул

перенос пр

1

x

2

x

2

v

1

v

.

реносимый импульс пропо не

.

21

vvm

Если число мо-

в единице объема равно

одольной компоненты им-

нален ве ичи

n ,

пульса в направлении оси

2

x

через единичную площадку в единицу вре-

мени равен величине

>

<

21

vvmn

. Угловые скобки в данном случае озна-

чают осреднение по большо числ . Поток импульса через еди-

ничную площадку в единицу времени ес

ке, то есть

му у молекул

ть напряжение трения на площад-

>

<

−

=

2121

vv

ρ

σ

. (2.7)

Знак минус в (2.7) поставлен потому, что положительные значения компо-

ненты скорости

2

v

должны переносить дефицит импульса в потоке с по-

ложительными значениями

21

σ

и

21

/ xdUd

. Между выражением (2.7) и

определением напряжений Рейнольдса

>

42

<

−

=

212

uu

1

ρ

τ

(2.8)

аналогия преднамеренная яжения, кот: напр орые возникают под действием

потока импульса, всегда могут быть записаны в виде выражений (2.7) и

(2.8), независимо от того, каким механизмом вызывается поток импульса.

Кинетическая теория газов определяет выражение в правой части (2.7)

следующим образом. Обозначим через

ξ

ст

среднюю длину свободного про-

бега между двумя последовательными олкновениями. Тогда молекула,

стартующая с уровня

ξ

−

=

2

x

,

овне

0

2

испытывает в среднем столкновение с дру-

гой молекулой на ур

=

x

(рис. 15).

Рис. 15. Молекулярный перенос в ламинарном сдвиговом течении.

Если принять допущение о том, что в результате столкновения состав-

ляющая импульса молекулы в направлении оси

1

x

«приспосабливается» к

новому окружению, молекула приобретает импульса, равную

величину

[

]

)()0(

11

ξ

−−= UUmM . (2.9)

Величина

M

равн

сит де

Правая выражения (2.9) может быть разложена в ряд Тэйлора:

а количеству импульса, теряемому окружающей средой

в плоскости

0

2

=x

, потому что движущаяся снизу вверх молекула прино-

фицит импульса по отношению к среднему импульсу в плоскости

.0

2

=x часть

⋅⋅⋅+−=

2

xd

m

xd

mM

ξξ

. (2.10)

1

2

1

Ud

Чл ная со второго, моены этого разложения, начи гут быть отброшены, если

2

xd

ξ

>>

. (2.11)

Локальны

1

2

1

UdUd

й масштаб длины

течения чистого сдвига определяется выра-

2

21

xdU

. (2.12)

Следовательно, условие (2.11) означает, что

l

жением

/()/(

2

210

dxdUdL ≡ )/

ξ

2

1

0

>>L (2.13)

Для воздуха комнатной температуры

6

107

−

⋅=

ξ

см, так что почти для

всех течений условие (2.13) с необходимостью удовлетворяется. Это, в

свою очередь, оз

.

начает, что разложение (2.10) можно представить при-

ближенно в виде

2

1

xd

Ud

mM

≅

(2.14)

В этой ростой модели величина

)/(

21

xdUd

ξ

.

п

ξ

есть част компоненты

скорости

1

v

, которая коррелирует с компонентой скорости

2

v

минус

поставлен в соответствии с соглашением о знаке напряжения

21

ь

знак(

σ

). Если

43

принять характерную скорость молекулярного движения скорость звука

в газе

a приближенно равную среднек

за

вадратичной скорости теплового

движения видеть, что

молекул, то легко

)/(

3

121

Сравнивая это выражение с (2.6), получаем, что

2

xdUda

ξρσ

= . (2.15)

ξ

ν

a)3/2(

=

, а число

з этих параме

Рейнольдса, составленное и тров, равно

2/3/)(

=

ν

ξ

a .

(2.1

Значение числа Рейнольдса оказывается величиной порядка единицы. И

это не случайно, поскольку вязкость среды определяется мо ек

6)

л улярным

движением с характерными масштабами скорости

a и длины

ξ

.

Характерные масштабы времени и длины, определяющие мол у-

лярный перенос.

Отношени средней длины свободного про

ек

е бега

ξ

к

l

называется

локальному масштабу длин

числом Кнудсена:

ы

,

2

3

0

L

где

aUM /

1

=

− числ а

ν

/)(

01

LUeR ⋅= − число Рейнольдса. В

большинстве течений

eRM

eR

M

Kn ==

ξ

(2.17)

о Маха,

<

, так что условие (2.13) удовлетворяется.

Характерный енной масштаб молекулярного движения – частота

столкновений

a/

врем

ξ

имеет типичное значение, например для воздуха ком-

натной температуры, равное

10

−

секунд. В качестве временного масшта-

ожет быть взята обратная величина градиен корости,

1

21

)/(

−

xdUd

. Для «быстрого» сдвига эта величина равна

4

10

−

секунд.

Ясно, что изменения в потоке среды происходят на интервалах времени

много больших, чем характерное время молекулярного движения (частота

столкновений). Можно сделать вывод о том, что тепловое движение не

может быть сильно нарушено течением среды: произойдет много тысяч

столкновени

ба течения м та с

й молекул, прежде чем течение пройдет вперед на заметное

рас

е ом

ом

Часть компоненты скорости

коррелирующая ости

стояние.

Корреляция между компонентами скорости молекулы

1

v

и

2

v

. Для

последующих целей полезно получить представлени о т , сколь хорошо

коррелируют молекулярные к поненты скорости

1

v

и

2

v

друг с другом.

1

v

, с компонентой скор

44

2

v

, пропорциональна

)/(

21

xddU

ξ

, как это определено согласно (2.14).

Оценка для быстрого сдвигового течения дает

4

21

107)/(

−

⋅=xddU

ξ

м .

1−

⋅c

Далее, коэффициент корреляции между компонентами скорости

и

может быть определен выражением

1

v

2

v

><

=

2

21

v

vv

C

. (2.18)

Сравнение (2.18) с (2.4) показывает, что при определении коэффициента

корреляции принято, что среднеквадратичные значения компонент скоро-

сти

и равны друг другу. С учетом полученных выше результатов

можно записать следующую оценку для коэффициента корреляции

1

v

2

v

><

⋅

≈

2

21

/

v

xdUd

C

ξ

. (2.19)

Поскольку знаменатель в (2.19) того же порядка величины, что и ско-

рость звука (

для воздуха комнатной температуры), зна-

чение коэффициента

, что свидетельствует о крайне плохой

корреляции. Если градиент средней скорости

оценить как

, коэффициент корреляции оказывается величиной порядка

, которая действительно имеет тенденцию быть экстремально ма-

лой в большинстве течений. Можно, таким образом, утверждать, что со-

стояние газа вряд ли может быть нарушено вследствие молекулярного пе-

реноса импульса. Другими словами, динамическое равновесие теплового

движения молекул в ламинарном сдвиговом течении газа с большой степе-

нью приближения то же самое, что

и состояние равновесия в неподвижном

газе. Следовательно, ламинарное сдвиговое течение, вероятно, не наруша-

ет уравнения состояния газа, если только отношение

невелико.

12

104,3

−

⋅⋅= cмa

6

102

−

⋅≈C

21

/ xdUd

01

/ LU

eRМ /

2

eRМ /

2

Забегая вперед, заметим, что коэффициент корреляции турбулентных

флуктуаций скорости не мал в неоднородном турбулентном течении. Сле-

довательно, «состояние турбулентности» не является независимым от поля

среднего течения. Наоборот, взаимодействие между средним течением и

турбулентностью имеет тенденцию быть очень сильным.

45

Оценка турбулентного потока импульса. Оценку турбулентного по-

тока импульса можно попытаться получить, рассматривая процесс случай-

ного перемещения жидких частиц в турбулентном сдвиговом течении. Та-

кой процесс рассмотрен в п. 1.4.3 для случая однородной турбулентности.

Пусть жидкая частица начинает свое движение в момент времени

0

=

t

от плоскости

вверх. Составляющая мгновенного значения импульса

частицы (на единицу объема) в направлении оси

равна

0

2

=x

1

x )0,0(

~

1

u

ρ

.

(

)0,0(

~

1

u

− мгновенная скорость частицы в плоскости

0

2

=

x

в момент

времени

). Если предположить, что частица не теряет своего импульса

при перемещении в направлении оси

, то она будет иметь дефицит им-

пульса

0=t

2

x

)0,0(

~

),(

~

121

utxuМ

ρρ

−=∆ на некотором расстоянии в момент

времени

2

x

t

. Используя рейнольдсовое разложение (1.3) для скорости, де-

фицит импульса можно записать в виде

[

][ ]

)0,0(),()0()(

121121

utxuUxUM

−

+

−

=

∆

ρ

.

Если вкладом турбулентности в дефицит импульса можно пренебречь и

если можно ограничиться первым членом разложения разности

в ряд Тэйлора,

))0()((

121

UxU −

,

2

1

2

xd

Ud

x ⋅

где градиент вычисляется в

плоскости

, дефицит импульса можно в таком случае аппроксимиро-

вать выражением

0

2

=x

2

1

2

xd

Ud

XM ⋅=∆

ρ

. (2.20)

Жидкая частица переносит в направлении оси

через единичную пло-

щадку в единицу времени объем среды со скоростью

2

x

dtXdv /

~

22

=

, так что

осредненный поток импульса в плоскости

можно записать в виде

0

2

=x

2

1

12

2

1

X

td

d

xd

Ud

⋅=

ρτ

. (2.21)

Угловые скобки здесь означают осреднение по всем жидким частицам,

которые движутся от плоскости

0

2

=

x

. Скорость дисперсии смещения

жидкой частицы можно записать как

46

>⋅<=⋅=

22

2

22 vX

td

Xd

XX

td

d

. (2.22)

Из (2.22) можно заключить, что если жидкая частица не обменивается не-

прерывно импульсом с её окружением, её скорость

должна оставаться

постоянной. В таком случае корреляция

2

v

>

⋅

<

22

vX

будет возрастать с

увеличением координаты частицы

. Это, конечно, нереалистично. Вме-

сто этого следует ожидать, что корреляция между величинами

и

для частицы будет уменьшаться по мере её перемещения. Если предполо-

жить, что величины

и становятся в основном некоррелированными

при значении

, сравнимым с некоторым линейным масштабом , кор-

реляцию

можно оценить как

2

X

2

X

2

v

2

X

2

v

2

X

L

l

>⋅<

22

vX

L

lvvX ⋅><≈>⋅<

2

222

, (2.23)

где

LL

Tvl ⋅><=

2

− лагранжевый линейный масштаб турбулентности.

Для однородной стационарной турбулентности плотности вероятности

турбулентного поля скорости, а вместе с ними и характеристические

функции лагранжевого и эйлерового полей, скорости одни и те же [3]. Это

означает, что для несжимаемого течения среднеквадратичные флуктуации

лагранжевого и эйлерового полей скорости совпадают:

><=><

22

αα

uv

.

Учитывая целый ряд грубых допущений, сделанных при выводе формулы

(2.21), допустимо в оценке (2.23), имея в виду также результаты п. 1.4.3.,

использовать вместо лагранжевых характерных масштабов длины и скоро-

сти эйлеровые масштабы

u

и .

ˆ

L

Таким образом, в окончательном виде оценку для турбулентного пото-

ка импульса можно записать в виде

2

1

121

ˆ

xd

Ud

Luc ⋅⋅⋅⋅=

ρτ

, (2.24)

где

− некоторый численный коэффициент.

1

c

Оценка корреляции (2.23) в действительности означает, что импульс

жидкой частицы в процессе ее перемещения на расстояния, сравнимые с

линейным интегральным масштабом турбулентности, не сохраняется. Сле-

довательно, эта оценка делает выражение (2.20) для дефицита импульса по

меньшей мере сомнительным.

47

Сопоставляя выражения (2.15) и (2.24), можно сказать, что множитель

при производной в выражении (2.24) представляет собой

вихревую (или

т

урбулентную) вязкость:

. (2.25) Luc

T

ˆ

1

ρν

=

Величины

и − функции пространства и времени. Они − свойства

течения жидкости, а не свойства самой жидкости (

как в случае молеку-

лярного переноса

). Конечно, это не очень многообещающая перспектива

для получения универсальной связи между величинами

u

ˆ

L

ji

τ

и .

ji

S

Реально турбулентность представляет собой флуктуационное движение

с широким спектром линейных масштабов. Вместе с тем, из (2.25) следует,

что крупномасштабные вихри вносят больший вклад в перенос импульса,

чем мелкомасштабные вихри. Другими словами, оценка турбулентного

потока импульса (2.24) указывает на крупномасштабный характер меха-

низма турбулентного переноса импульса.

Однако оценка (2.23) свидетельствует о физической некорректности

оценки

турбулентного потока импульса (2.24). Действительно, если опре-

делить локальный линейный масштаб среднего течения в виде выражения

(2.12), то аппроксимация

212121

/)0()( dxdUxUxU ⋅

=

−

может быть спра-

ведливой для всех значений

, если только

2

x

LL

2

1

0

>> , чтобы можно бы-

ло пренебречь членами более высокого порядка в разложении в ряд Тэйло-

ра для дефицита переносимого импульса (2.20). В гл. 1 отмечалось, что

крупномасштабные турбулентные вихри могут иметь размеры, сравнимые

по порядку величины с характерными размерами области турбулентного

движения. Иллюстрацией может служить «типичный вихрь», показанный

на рис. 11. Следовательно, для турбулентности

характерно то, что линей-

ный масштаб среднего течения

и интегральный масштаб турбулентно-

сти

(сравнимый с размером энергонесущих вихрей), величины одного

порядка, то есть турбулентное число Кнудсена

есть величина

порядка единицы.

0

L

LLKn /

0

=

Таким образом, турбулентность представляет собой физическую систе-

му, для которой не представляется возможным недвусмысленно указать

малый параметр, по которому можно было бы корректно провести «сокра-

щение информации» путем соответствующих разложений. Поэтому обры-

вание разложения в ряд Тэйлора при получении (2.20) трудно обосновать.

Снова можно указать на то,

что турбулентность есть свойство течения

сплошной среды. Турбулентность сильно взаимодействует со своим окру-

48

жением, а состояние турбулентности сильно зависит от того течения, в

котором она сама находится.

Однако притягательность модели «градиентной диффузии» (2.24) в си-

лу ее простоты столь сильна, что развитие этого приближения продолжает-

ся и до сих пор и успешно используется при решении целого ряда задач

турбулентного переноса. Поэтому в следующем параграфе

дается функ-

циональная формулировка для определяющей связи тензора турбулентных

напряжений с характеристиками поля скорости. Показывается, как можно

установить локальную связь между турбулентными напряжениями и сред-

ним тензором скоростей деформаций, не обращаясь к аналогии с теорией

молекулярного переноса, а используя иные физические аргументы.

В заключение необходимо сделать замечание о пренебрежении вкладом

турбулентного

импульса

[

]

)0,0(),(

1211

utxuu −

≡

∆

ρ

при получении ап-

проксимации дефицита импульса в виде выражения (2.20). Поток импуль-

са, связанный с членом

1

u

∆

ρ

, равен

>

∆

⋅

<

12

uu

ρ

(угловые скобки озна-

чают осреднение по большому числу частиц). Разность

1

u

∆

будет мала

для поперечных расстояний малых по сравнению с масштабом

, но она

будет значительна для расстояний

L

Lx

∝

2

, так что нет a priori никаких

разумных доводов в пользу пренебрежения этим вкладом. Это еще один

довод, свидетельствующий о сомнительности аналогий между молекуляр-

ным и турбулентным переносом.

2.3. Турбулентные напряжения как функционал поля

скорости

Для того чтобы глубже проникнуть в сущность проблемы замыкания

уравнения Рейнольдса (2.5), обратимся к определяющим полевым уравне-

ниям для турбулентной флуктуации скорости. Уравнение для вектора тур-

булентной флуктуации скорости легко получить вычитанием уравнения

(2.2) из уравнения Навье

− Стокса (1.1), в котором мгновенные поля ско-

рости и давления заменены декомпозициями Рейнольдса (1.3). Уравнение

для турбулентной флуктуации скорости

имеет вид

),( txu

i

G

.

1

2

j

ji

i

ij

i

j

i

j

i

j

i

x

uu

u

x

P

x

U

u

x

u

x

u

U

t

u

∂

>

<

∂

+∇+

∂

⋅−

∂

⋅−

∂

⋅−=

∂

⋅+

∂

ν

ρ

(2.26)

Уравнение (2.26) получается вычитанием уравнения (2.2) из уравнения

Навье

− Стокса (1.1), в котором мгновенные значения скорости и давления

заменены декомпозициями Рейнольдса (1.3). Уравнение неразрывности для

49

турбулентной флуктуации скорости получается аналогично при использо-

вании уравнений (1.2) и (2.3):

.0=

∂

i

x

u

(2.27)

Решение уравнений (2.26) и (2.27) может быть записано в общей форме

[

]

,),(,

,,;),(),0,(),,(),(

tsy

txsyuyusyUtxu

ii

∞−∈Ξ∈

ℑ=

Ξ∂

G

(2.28)

где обозначает функционал,

[]

•ℑ

i

Ξ

− объем жидкости,

Ξ

∂

− ограничи-

вающая этот объем поверхность.

Выражение (2.28) означает, что турбулентная флуктуация скорости есть

функционал всей предыстории среднего поля скорости с неявной зависи-

мостью от его начальных и граничных условий. (Термин функционал здесь

используется в его широком математическом смысле: любая величина оп-

ределяется функцией). Это выражение позволяет в свою очередь предста-

вить

в явном виде тензор турбулентных напряжений ед. массы жидкости

><≡

jiji

uu

τ

, также как функционал всей предыстории среднего поля

скорости. При этом, однако, возникает серьезная проблема зависимости

величи

ji

τ

от начальных и граничных условий турбулентного поля скоро-

сти. В разд. 1.2 уже упоминалось о том, что нет надежды получить описа-

ние эволюции напряжений Рейнольдса в замкнутой форме, если нет де-

тальной зависимости от указанных начальных и граничных условий.

2.3.1. Локальное приближение для функционала напряжений

Рейнольдса

Для турбулентных течений (вдали от твердых границ), которые доста-

точно долго эволюционировали после их возникновения, не кажется нера-

зумным предположить, что начальные и граничные условия турбулентного

поля скорости

),( txu

i

G

, за исключением тех же условий для тензора

ij

τ

,

можно описать с помощью линейного и временного масштаба турбулент-

ного поля скорости. С принятием этого решающего допущения выражение

для тензора турбулентных напряжений может быть записано в виде

[

]

.),(,

,,;),(),,(),,(

tsy

txsyTsyLsyU

ijij

∞−∈Ξ∈

ℑ=

G

τ

(2.29)

50

Курбацкий А.Ф. Лекции по турбулентности. Часть 1

Подождите немного. Документ загружается.