Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи

Подождите немного. Документ загружается.

А. И. Козко В. Г. Чирский

Задачи с параметром

и другие сложные задачи

Москва

Издательство МЦНМО

2007

УДК 512

ББК 22.141

К59

Козко А. И., Чирский В. Г.

Задачи с параметром и другие сложные задачи. — М.:

МЦНМО, 2007. — 296 с.

ISBN 978-5-94057-270-1

Книга посвящена решению задач с параметрами. Помимо стан-

дартных сведений в ней приведены оригинальные методы и приемы

решения различных сложных задач. Кроме того, в книге рассмотре-

ны задачи, связанные с методом математической индукции, и задачи

по стереометрии. Большинство разбираемых авторами задач взято из

вариантов вступительных экзаменов в МГУ.

Во втор ой части книги приведены варианты вступительных экза-

менов 2003—2006 гг.

Для учащихся старших классов, преподавателей математики и аби-

туриентов.

ББК 22.141

Козко Артем Иванович, Чирский Владимир Григорьевич

ЗАДАЧИ С ПАРАМЕТРОМ И ДРУГИЕ СЛОЖНЫЕ ЗАДАЧИ

Формат 60 × 90

. Бумага офсетная. Печать офсетная.

Печ. л. 18,5. Тираж 3000 экз. Заказ № .

Издательство Московского центра

непрерывного математического образования.

119002, Москва, Большой Власьевский пер., 11. Тел. 241-74-83.

Отпечатано с готовых диапозитивов в ФГУП «Полиграфические ресурсы»

ISBN 978-5-94057-270-1

 Козко А. И., Чирский В. Г., 2007

 МЦНМО, 2007

Оглавление

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1. Основные задачи и методы их решения 8

§1.1. Простейшие уравнения и неравенства с параметром . . . 8

§1.2. Простейшие задачи с модулем . . . . . . . . . . . . . . . 19

§1.3. Решение обратных задач и задач, в которых параметр

рассматривается как отдельная переменная . . . . . . . . 24

§1.4. Тригонометрические уравнения и неравенства с пара-

метром . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

§1.5. Уравнения, сводящиеся к исследованию квадратного урав-

нения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

§1.6. Выделение полных квад ратов и неотрицательных выра-

жений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

§1.7. Разложение на множители . . . . . . . . . . . . . . . . . . 53

§1.8. Теорема Виета для уравнения высокого порядка . . . . . 60

§1.9. Задачи на единственн ость и количество решений . . . . 66

§1.10. Задачи, решаемые с использованием симметрий . . . . 72

§1.11. Задачи, основанные на применении некоторых нера-

венств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

§1.12. Решения, основанные на нахождении наибольших и наи-

меньших значений (метод минимаксов) . . . . . . . . . . 84

§1.13. Решение задач при помощи графика . . . . . . . . . . . 89

§1.14. Метод областей . . . . . . . . . . . . . . . . . . . . . . . 98

§1.15. Задачи на целые числа . . . . . . . . . . . . . . . . . . . 106

§1.16. Задачи с целой и дробной частью числа . . . . . . . . . 114

§1.17. Введение параметра для решения задач . . . . . . . . . 119

4 Оглавление

§1.18. Использование особенностей функций (монотонность,

чётность, нечётность, непрерывность) . . . . . . . . . . . 124

§1.19. Задачи с итерациями . . . . . . . . . . . . . . . . . . . . 132

§1.20. Задачи с требованием выполнения (или невып олне ния)

неравенства для всех значений параметра . . . . . . . . . 135

§1.21. Геометрические задачи с элементами алгебры . . . . . . 139

§1.22. Задачи алгебры с использованием г еоме трии . . . . . . 141

2. Варианты вступительных экзаменов 150

§2.1. Варианты 2003 года . . . . . . . . . . . . . . . . . . . . . 150

§2.2. Варианты 2004 года . . . . . . . . . . . . . . . . . . . . . 210

§2.3. Варианты 2005 года . . . . . . . . . . . . . . . . . . . . . 259

§2.4. Варианты 2006 года . . . . . . . . . . . . . . . . . . . . . 292

Введение

Книга посвящена решению задач с параметрами, а также различ-

ных задач, связанных с методом математической индукции, и задач

по стереометрии — теме, которой боятся многие абитуриенты. Умение

решать такие задачи считается признаком отличного знания матема-

тики. Некоторые при подготовке к экзаменам боятся даже бр аться за

эти задачи, думая, что у них всё равно ничего не получи тся. Вместе с

тем часто для решения задачи с параметром нужно просто использо-

вать свой здравый смысл, и решение окажется простым и понятным!

Поясним сказанное примером и решим «трудную» задачу.

Найдите такие значения параметра a < 1, для которых решения

неравенства x

− (a + 1)x + a 6 0 образуют отрезок, длина которого

больше 3.

Что же делать? Как упоминалось выше, использовать здравый

смысл! Если бы вместо переменного параметра a в задачу входило

какое-то конкретное число, например число −4, то наше неравенство

приняло бы вид x

+3x−4 6 0. Такие-то неравенства мы реш аем легко!

Найдя корни многочлена x

+ 3x − 4 = 0, а это будут числа x

= −4,

= 1, преобразуем наше неравенство к виду (x + 4)(x − 1) 6 0.

Для его решения применим известный метод интервалов и получим

x ∈ [−4; 1]. Длина этого отрезка равна 5, следовательно, число −4 удо-

влетворяет условию задачи. Так давайте поступать по той же схеме и

в общем случае, с переменным параметром. Найдём корни многочлена

−(a + 1)x + a. Решим для этого уравнение x

−(a + 1)x + a = 0. Его

дискриминант равен (a + 1)

− 4a = (a

+ 2a + 1) − 4a = a

− 2a + 1 =

= (a−1)

, поэтому корнями будут числа x

1,2

(a+1)±(a−1)

, т. е. числа

= a, x

= 1, откуда следует, что исходное неравенство можно пе-

реписать в виде (x − a)(x − 1) 6 0. По условию задачи a < 1, значит,

вновь используя метод интервалов, мы находим, что решением этого

неравенства является отрез ок [a; 1]. Длина отрезка равна числу 1 − a,

и условие задачи выполн яется, если 1 − a > 3, т. е. a < −2.

Ну что же, это не совсем простое реш ени е, но и не слишком-то

сложное, доступное каждому!

Первая цель предлагаемой книги состоит как раз в том, чтобы по-

мочь желающим научиться решать задачи с параметрами. И начинать

следует именно с простых задач. Начало книги и начала большинства

параграфов содержат достаточно простые задачи. Однако если Вы

обратите внимание на н азвани я факультетов и номера этих решён-

ных простых задач, под которыми они стоят в вариантах, то поймёте,

6 Введение

что многие из задач с параметрами, которые даются на вступительных

экзаменах и которых Вы так опасались, вполне Вам по силам.

При решении задач с параметрами приходится всё время произво-

дить несложные, но последовательные рассуждения, составлять для

себя логическую схему решаемой задачи. Поэтому такие задачи —

незаменимое средство для тренировки логического мышления. Их ре-

шение позволяет намного лучше понять обычные, без параметров, за-

дачи. А привычка к математическим рассуждениям очень полезна

при изучении высшей математики и использовании полученных зна-

ний впоследствии. Также будет полезным знакомство с методом ма-

тематической индукции — основой доказательства теорем из высшей

математики. Знание стер еоме трии , умение решать задачи развивает

пространственное, образное мышление и также полезно для разви-

тия математических способностей обучающегося. Ведь математиче-

ские методы приобретают всё большее значение в развитии и приме-

нении многих наук и технологий.

Применение метода интервалов предполагает автоматический учёт

ОДЗ при расставлении точек н а действительной оси. Условия, зада-

ющие ОДЗ, специально выписаны в тех задачах, где проверка этих

условий является важной составной частью решения.

Не стоит думать, что книга посвящена только простым задачам.

В ней рассмотр ены многие оригинальные методы и приёмы решения

весьма трудных задач. Достаточно взглянуть на перечень параграфов,

чтобы убедиться в том, что книга содержит как часто используемые,

так и малоизвестные способы решения задач. А изучаемый материал

подобран так, чтобы проиллюстрировать преимущества того или иного

способа.

В книге много з адач и упражнений. Многие задачи составлены ав-

торами. Большин ство задач взято из вступительных экзаменов в МГУ.

Обозначения вида

(факультет почвоведения (май), 2002, № 6(7))

означают, что задача предлагалась на майской олимпиаде МГУ (да-

ющей право поступления на факультет почвоведения) в 2002 году

в качестве шестой задачи в варианте из семи задач. ЕГЭ (демо)

обозначает, что задача взята из предварительного демонстрационного

варианта единого государственного э кз амен а (ЕГЭ).

Одним словом, основной ц ел ью авторов было написание книги, ко-

торая поможет при подготовке к поступлению в большинство высших

учебных заведений, поскольку содержит задачи всех уровней, от про-

Введение 7

стых до самых трудных. Она даёт разные методы решения этих задач,

рассчитанные на самый различный уровень подготовки читателя.

Вновь подчеркнём, что основой для усвоения материала мы с чита-

ем здравый смысл читателя, а не только и не столько его предвари-

тельные знания. В жизни здравый смысл — надёжная опора, поэ тому

мы надеемся, что он поможет Вам и на вступительных испытаниях.

Мы будем рады, если наша книга поможет Вам более уверенно ис-

пользовать здравый смысл на всех видах испытаний по математике и

выйти из них счастливым победителем!

Желаем Вам успеха!

Часть 1

Основные задачи и методы их решения

§1.1. Простейшие уравнения

и неравенства с параметром

Цель данного парагр афа состоит в том, чтобы на простейших при-

мерах познакомить читателя с задачами с параметрами. Для решения

данных задач ничего кроме здравого смысла не требуется. Если сразу

не понятно, как решать задачу, мы советуем читателю вчитываться в

неё до тех пор, пока не станет ясно условие.

В некоторых задачах для нахождения параметров достаточно про-

сто подставлять в неравенство (уравнение или систему) точку: напри-

мер, так решаются задачи 1, 2, 5 и следующий пример.

Пример 1 (ЕГЭ, 2003, № B4). При каком наибольшем отрицатель-

ном значении a функция

y = sin



24x +

aπ

100



имеет максимум в точке x

= π?

Решение. Максимумы функции sin t достигаются в точках вида

π/2 + 2πn, n ∈ Z. Следовательно, чтобы у исходной функции дости-

гался максимум в точке x

= π, должно существовать такое число

n ∈ Z, что

24π +

aπ

100

+ 2πn, n ∈ Z ⇐⇒

100

+ 2m, m ∈ Z ⇐⇒

⇐⇒ a = 50 + 200m, m ∈ Z.

Остаётся лишь выбрать среди чисел вида a = 50 + 200m, m ∈ Z,

наибольшее отрицательное. Это будет число −150, получающееся при

m = −1, так как если m > 0, то 50 + 200m > 50.

Ответ. a = −150.

§1.1. Простейшие уравнения и неравенства с параметром 9

Пример 2. При всех a решите неравенство

x − a

x − a − 1

6 0.

Решение. При любом фиксированном значении a это обычное ра-

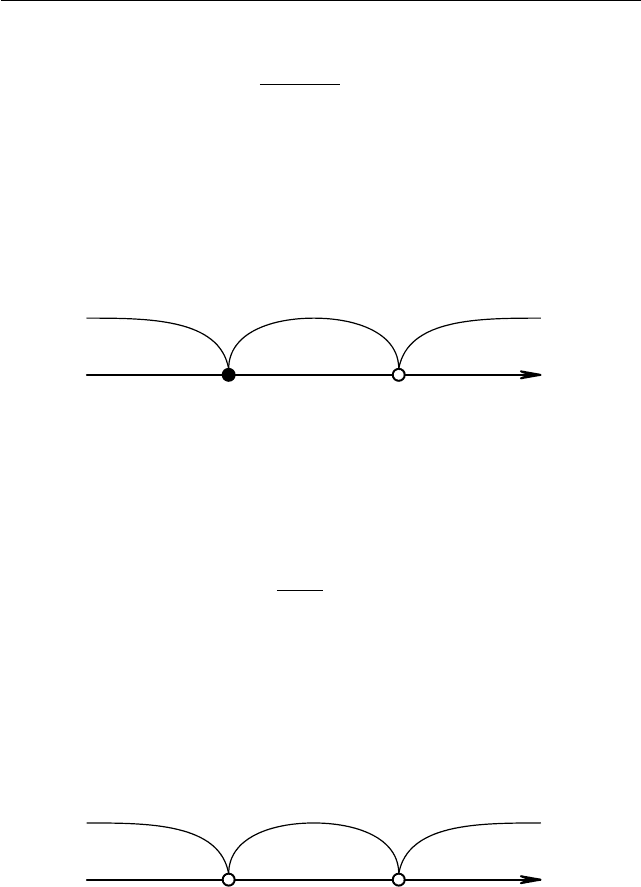
циональное неравенство. Поэтому к нему можно применить метод ин-

тервалов. Напомним, что для этого следует расположить на числовой

оси числа a и a + 1, в которых обращаются в нуль числитель и зна-

менатель соответственно. Ясно, что при всех a число a + 1 больше

чем a. Поэтому получаем такое расположение точек, как показано на

рис. 1.1.

+ − +

a + 1

Рис. 1.1

Ответ. x ∈ [a; a + 1) при любом a.

Рассмотрим ещё один пример.

Пример 3. При всех a решите неравенство

x − 1

x − a

> 0.

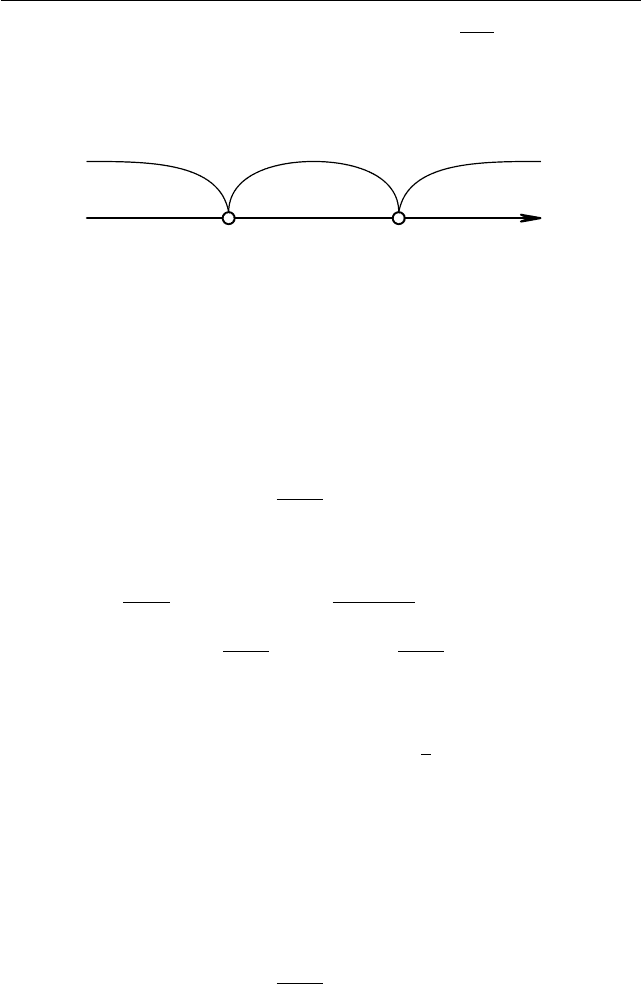
Решение. Как и выше, буде м применять метод интервалов. Од-

нако здесь возникает небольшая трудность — мы не знаем, как распо-

ложены числа 1 и a. Ведь a может быть как меньше 1, так и больше

или равно 1. Но это означает, что нам следует рассмотреть эти три

случая.

I. Пусть a < 1. Тогда получаем такое расположение точек, как

показано на рис. 1.2.

+ − +

Рис. 1.2

Метод инте рвалов даёт часть ответа: если a < 1, то x ∈ (−∞; a) ∪

∪ (1; +∞).

10 Часть 1. Основные задачи и методы их решения

II. Пусть a = 1. Тогда получаем неравенство

x−1

> 0, при x 6= 1

равносильное верному неравенству 1 > 0. Его решения — вся область

определения неравенства, т. е. (−∞; 1) ∪ (1; +∞).

III. Пусть a > 1. Тогда точки расположены, как показано на рис. 1.3.

+ − +

a x

Рис. 1.3

Метод интервалов приводит к частичному ответу: если a > 1, то

x ∈ (−∞; 1) ∪ (a; +∞).

Объединим части ответов и получим окончательный результат.

Ответ. Если a < 1, то x ∈ (−∞; a) ∪ (1; +∞); если a = 1, то

x ∈ (−∞; 1) ∪ (1; +∞); если a > 1, то x ∈ (−∞; 1) ∪ (a; +∞).

Пример 4. При всех a решите неравенство

x + a

> 1.

Решение. Преобразуем неравенство:

x + a

− 1 > 0 ⇐⇒

x − x − a

x + a

> 0 ⇐⇒

⇐⇒

−a

x + a

> 0 ⇐⇒

x + a

< 0.

При a > 0 это неравенство равносильно неравенству x + a < 0,

x < −a, и его решения — x ∈ (−∞; −a).

При a = 0 получаем неверное неравенство

< 0, 0 < 0, у которого,

разумеется, нет решений.

При a < 0 это неравенство равносильно такому: x + a > 0, или

x > −a, имеющему ре шен ия x ∈ (−a; +∞).

Ответ. Если a < 0, то x ∈ (−a; +∞); если a = 0, то x ∈ ∅; если

a > 0, то x ∈ (−∞; −a).

Рассмотрим ещё один простой пример.

Пример 5. При всех a решите неравенство

x + a

> 1.