Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи
Подождите немного. Документ загружается.


§1.8. Теорема Виета для уравнения высокого порядка 61
Отсюда, раскрывая скобки и приравнивая коэффициенты при одина-
ковых степенях, приходим к следующим формулам:
x
1
+ x
2
+ . . . + x
n
= −a
n−1
/a
n
,
(x
1
x
2
+ x
1
x
3
+ x
1
x
4
+ . . . + x
1
x
n
) +
+ (x
2
x
3
+ x
2
x
4
+ . . . + x
2
x
n
) + . . . + x
n−1
x
n
= a
n−2
/a
n
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,
P
i
1
<i
2
<...<i
k
x
i
1
x
i
2
. . . x
i
k
= (−1)
k
a
n−k
/a
n
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,
x
1
x
2
. . . x
n
= (−1)
n
a
0
/a
n
,
которые носят название формул Виета.
I. Для квадратного уравнения a
2
x
2
+ a
1
x + a
0
= 0, a
2
6= 0, где
x
1
, x
2
— корни уравнения (случай D > 0), общие формулы принимают
вид
(
x
1
+ x
2
= −a
1
/a
2
,
x
1
x
2
= a
0
/a
2
.
II. Для кубического уравнения a
3
x
3
+ a
2
x
2
+ a
1
x + a
0
= 0, a
3
6= 0,
где x
1
, x
2
, x
3
— корни уравнения, общи е формулы принимают вид
x
1
+ x
2
+ x
3
= −a
2
/a
3
,
x
1
x
2
+ x
1
x
3
+ x
2
x
3
= a
1
/a
3
,
x
1
x
2
x
3
= −a
0
/a
3
.
III. Для уравнения четвёртой степени a
4
x
4
+a
3
x
3
+a
2
x
2
+a
1
x+a
0
=0,
a
4
6= 0, где x
1
, x
2
, x
3
, x
4
— корни уравнения, общие формулы принима-
ют вид
x
1
+ x
2
+ x
3
+ x
4
= −a
3
/a
4
,
x
1
x
2
+ x
1
x
3
+ x
1
x
4
+ x
2
x
3
+ x
2
x
4
+ x
3
x
4
= a
2
/a
4
,
x
1
x
2
x
3
+ x
1
x
2
x
4
+ x
2
x
3
x
4
= −a
1
/a
4
,
x
1
x
2
x
3
x
4
= a
0
/a
4
.
Пример 22 (социологический факультет, 2003, № 6). Определи-
те все значения параметра a при каждом из которых три различных
корня уравнения
x
3
+ (a
2
− 9a)x
2
+ 8ax − 64 = 0
образуют геометрическую прогрессию. Найдите эти корни.

62 Часть 1. Основные задачи и методы их решения
Решение. Пусть q — знаменатель геометрической прогрессии. То-
гда корни связаны соотношением x
2
= qx
1
, x
3
= q
2
x
1
. По теореме
Виета x
1
x
2
x
3
= 64 или (qx
1
)
3
= 64, откуда мы получаем x
2
= 4. Запи-
шем теорему Виета для x
1
= q
−1
x
2
= 4q
−1
, x
2
= 4, x
3
= qx
2
= 4q.
4(q
−1
+ 1 + q) = −(a
2
− 9a),
16(q + 1 + q
−1
) = 8a,
x
2
= 4.
Заметим, что a 6= 0, так как иначе уравнение q+1+q
−1
= 0 решений не
имеет и, следовательно, этот случай противоречит условию существо-
вания трёх раз лич ных корней. Поделив первое уравнение на второе,
получаем
2 = −(a − 9) ⇐⇒ a = 7.
Теперь из второго уравнения находим
q + 1 + q
−1
= 7/2 ⇐⇒ q
2
− (5/2)q + 1 = 0 ⇐⇒
"
q = 2,
q = 1/2.
Пусть q = 2. Тогда x
1
= 2, x
2
= 4, x
3
= 8. Пусть q = 1/2. Тогда x
1
= 8,
x
2
= 4, x
3
= 2. В обоих случаях получае м, что корнями исходного
уравнения являются числа 2, 4, 8.
Заметим, что после нахождени я корня x
2
= 4 уравнение можно
решить проще: подставим x = x
2
= 4 в исходное уравнение
4
3
+ 16(a
2
− 9a) + 32a − 64 = 0 ⇐⇒ a
2
− 7a = 0.
Получаем два значения параметра a: a = 0, a = 7. Как и ранее, дока-
зываем, что случай a = 0 невозможен. Для a = 7 уравнение принимает
вид
x
3
− 14x + 56x − 64 = 0 ⇐⇒ (x − 4)(x
2
− 10x + 16) = 0 ⇐⇒
⇐⇒ (x − 4)(x − 2)(x − 8) = 0.
Отсюда получаем искомый ответ.
Ответ. a = 7, корни уравнения 2, 4, 8.
Пример 23 (психологический факультет, 1992, № 4). Найдите все
значения параметров a и b, при которых найдутся два различных
корня уравнения x
3
− 5x
2
+ 7x = a, которые будут также корнями
уравнения x
3
− 8x + b = 0.

§1.8. Теорема Виета для уравнения высокого порядка 63
Решение. Решим задачу двумя способами.
I. Пусть x
1
, x
2
, x
3
— решения уравнения
1
x
3
−5x
2
+7x = a, причём
x
1
6= x
2
. Пусть x
1
, x
2
, x
0
3
— решения уравнения x
3
− 8x + b = 0.
Так как корни x
1
, x
2
удовлетворяют сразу д вум уравнениям
x
3
− 5x
2
+ 7x = a и x
3
− 8x + b = 0,
они же удовлетворяют уравнению (левое часть которого разность двух
полиномов)
−5x
2
+ 15x − (a + b) = 0 ⇐⇒ x
2
− 3x +
a + b
5
= 0.
По теореме Виета для квадратного уравнения находим
x
1
+ x
2
= 3, (1.5)
x
1
x
2
= (a + b)/5. (1.6)
Запишем теорему Виета для уравнений x
3
−5x
2
+7x = a и x
3
−8x+b = 0 :
x
1
+ x
2
+ x
3
= 5,
x
1
x
2
+ x
1
x
3
+ x
2
x
3
= 7,
x
1
x
2
x
3
= a,
x
1
+ x
2
+ x
0
3
= 0,
x
1
x
2
+ x
1
x
0
3
+ x
2
x
0
3
= −8,
x
1
x
2
x
0
3
= −b
⇐⇒
x
3
= 2,
(a + b)/5 + 3x
3
= 7,
a + b
5
x
3
= a,
3 + x
0
3
= 0,
(a + b)/5 + 3x
0
3
= −8,
a + b
5
x
0
3
= −b.
Здесь мы воспользовались соотношениями (1.5)–(1.6). Далее мы нахо-
дим x
3
= 2, (a + b)/5 = 1, x
0
3
= −3, a =
a+b
5
x
3
= x
3
= 2, b = −
a+b
5
x
0
3
=
= −x
0
3
= 3.
Проверка. Для a = 2, b = 3 исходные уравнения принимают вид
x
3
− 5x
2
+ 7x − 2 = 0,
x
3
− 8x + 3 = 0.
1
Из существования двух корней x
1
, x
2
для многочлена третьей степени
ax
3
+ bx
2
+ cx + d = 0
вытекает существование третьего корня. Действительно, достаточно исходный
многочлен разделить на (x − x
1
)(x − x
2
).

64 Часть 1. Основные задачи и методы их решения
Из соотношений (1.5)–(1.6) можем предположить, что x
1,2
=
3±
√
5
2
—
корни уравнений. Действительно, подстановкой убеждаемся в спра-
ведливости предположения.
Приведём решение без использования теоремы Виета.
II. Пусть x
1
и x
2
— два различных решения уравнения
x
3
− 5x
2
+ 7x = a.
Для определенности будем считать, что x
1
> x
2
. Поскольку x
1
и x
2
удовлетворяют уравнению x
3
− 5x
2
+ 7x = a, мы получаем
(
x
3
1
− 5x
2
1
+ 7x
1
= a,
x
3
2
− 5x
3
2
+ 7x
2
= a.
Вычитая из первого уравнен ия второе (и учитывая, что x
1
− x
2
> 0),
получаем
(x
3
1
− x
3
2
) − 5(x
2
1
− x
2
2
) + 7(x
1
− x
2
) = 0 ⇐⇒
⇐⇒ (x
1
− x
2
)(x
2
1
+ x
1
x
2
+ x
2
2
− 5(x
1
+ x
2
) + 7) = 0 ⇐⇒
⇐⇒ (x
1
+ x
2
)
2
− 5(x
1
+ x
2
) − x
1
x
2
+ 7 = 0 .
Из того, что x
1
и x
2
удовлетворяют второму уравнен ию, т. е.
(
x
3
1
− 8x
1
+ b = 0 ,
x
3
2
− 8x
2
+ b = 0 ,
вытекает, ч то
(x
3
1
− x
3
2
) − 8(x
1
− x
2
) = 0 ⇐⇒
⇐⇒ (x
1
− x
2
)(x
2
1
+ x
1
x
2
+ x
2
2
− 8) = 0 ⇐⇒
⇐⇒ (x
1
+ x
2
)
2
− x
1
x
2
− 8 = 0 .
Таким образом, x
1
и x
2
удовлетворяют системе
(
(x
1
+ x
2
)
2
− 5(x
1
+ x
2
) − x
1
x
2
+ 7 = 0 ,
(x
1
+ x
2
)
2
− x
1
x
2
− 8 = 0
⇐⇒
⇐⇒
(
−5(x
1
+ x
2
) + 15 = 0,
(x
1
+ x
2
)
2
− x
1
x
2
− 8 = 0
⇐⇒
(
x
1
+ x
2
= 3,
x
1
x
2
= 1.
Следовательно, x
1
и x
2
удовлетворяют уравнению
x
2
− 3x + 1 = 0, (1.7)
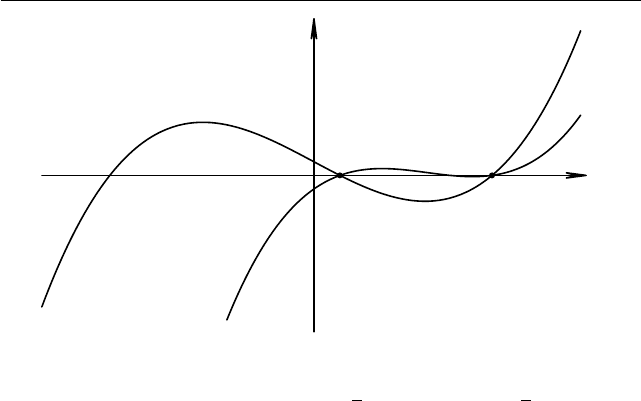
§1.8. Теорема Виета для уравнения высокого порядка 65
x
y
x
1
x
2
x
3
− 8x + 3 = 0
x
3
− 5x
2
+ 7x = 2
Рис. 1.36
решая которое, находим x
1
= (3 +
√
5)/2; x
2
= (3 −
√
5)/2. Теперь,
используя уравнение (1.7), найдем значение параметра a:
a = x
3
1
− 5x
2
1
+ 7x
1
= x
1
(x
2
1
− 5x
1
+ 7) = x
1
(x
2
1
− 3x
1
+ 1) − 2x
1
+ 6
=
= x
1
(−2x
1
+ 6) = −2(x
2
1
− 3x
1
+ 1) + 2 = 2,
и параметра b
−b = x
3
1
− 8x
1
= x
1
(x
2
1
− 3x
1
+ 1) + 3x
1
− 9
= x
1
(3x
1
− 9) =
= 3(x
2
1
− 3x
1
+ 1) − 3 = −3.
Ответ. a = 2, b = 3.
Задача 124 (географический факультет (июль), 2002, № 3 (6)).
Квадратное уравнение x
2
−6px + q = 0 имеет два различных корня x
1
и x
2
. Числа p, x
1
, x
2
, q — четыре последовательных члена геометри-
ческой прогрессии. Найдите x
1
и x
2
.
Задача 125 (географический факультет (июль), 1993, № 5). При
каких значениях a четыре корня уравнения
x
4
+ (a − 5)x
2
+ (a + 2)
2
= 0
являются последовательными членами арифметической прогрессии?
Задача 126 (физический факультет (июль), 1993, № 7). Уравнение
ax
2
+ bx + 2 = 0, где a < 0, имеет одним из с воих корней число x = 3.
Решите уравнение
ax
4
+ bx
2
+ 2 = 0.

66 Часть 1. Основные задачи и методы их решения
Задача 127 (психологический факультет, 1992, № 4). Найдите все
значения параметров u и v, при которых найдутся два р азли чны х
корня уравнения x(x
2
+ x − 8) = u, которые будут также корнями
уравнения x(x
2
− 6) = v.
Задача 128 (социологический факультет, 2003, № 6). Определите
все значения параметра, при каждом из которых три различных корня
уравнения x
3
+ (a
2
−15a)x
2
+ 12ax −216 = 0 образуют геометрическую
прогрессию. Найдите эти корни.
Задача 129 (механико-математический факультет, 1972, № 5). Да-
ны три уравнения с действительными коэффициентами:
x
2
− (a + b)x + 8 = 0, x
2
− b(b + 1)x + c = 0, x
4
− b(b + 1)x
2
+ c = 0.
Каждое из них имеет по крайней мере один действительный корень.
Известно, что корни первого уравнения больше единицы. Известно
также, что все корни первого уравнения являются корнями третье-
го уравнения и хотя бы один корень первого уравнения удовлетворяет
второму уравнению. Найдите числа a, b, c, если b > 3.
Ответы. 124. (−3; 9), (2; 4). 125. a = −5, a = −5/13. 126. x = ±
√
3.
127. u = 6, v = 4. 128. a = 13, корни уравнения 2, 6, 18. 129. a = 2, b = 4,
c = 64.
§1.9. Задачи на единственность
и количество решений
Введём обозначение: f
a
(x) означает, что функция f(x) может за-
висеть от параметра a (или нескольких параметров). Основной темой
данного параграфа является разбор следующей задачи.
Задача A. Найдите все значения параметра a (или нескольких
параметров), при которых уравнение (или неравенство) f
a
(x) = 0
(f
a
(x) 6 0) имеет единственное решение.
Напомним определение чётности и нечётности функции.
Определение 1.9.1. Если область определения функции f(x) сим-
метрична относительно точки x = 0 и f(−x) = f(x), то функция f(x)
чётная, если f(−x) = −f(x), то функция f(x) нечётная.
§1.9. Задачи на единственность и количество решений 67
x
y
−x
0
x
0
0
f(x)
x
y
0
f(x)
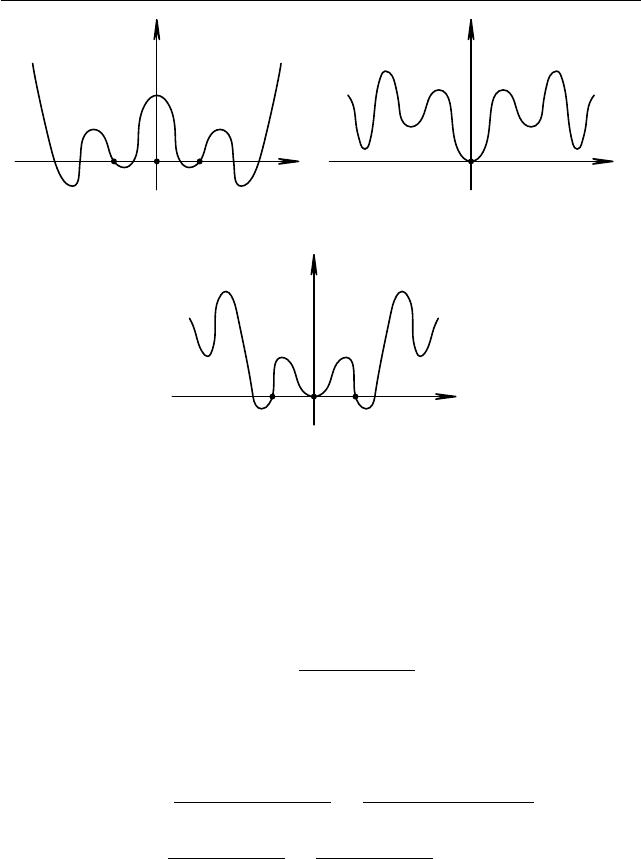
Рис. 1.37. f(x
0
) = f(−x
0
) = 0 Рис. 1.38. f(0) = 0
x
y
−x
0
x
0
0
f(x)
Рис. 1.39. f(x
0
) = f(−x
0
) = f(0) = 0
Пример 24. Функции
f
1
(x) = |sin x|,
f
2
(x) = c os x,
f
3
(x) = x
4
− 3x
2
,
f
4
(x) =
tg x · (7
x
− 1)
7
x
+ 1
чётные. Для первых трёх это очевидно. Для функции f
4
(x) проверим,
что она чётная:
f
4
(−x) =
tg(−x) · (7
−x
− 1)
7
−x
+ 1
=
−tg x · 7
−x
(1 − 7
x
)
7
−x
(1 + 7
x
)
=
= −
tg x · (1 − 7
x
)
(1 + 7
x
)
=
tg x · (7
x
− 1)
7
x
+ 1
= f
4
(x).
Пусть при решении задачи A функция f
a
(x) оказалась чётной. То-
гда если x
0
является решением задачи, то и −x
0
— решени е задачи (см.
рис. 1.37), поскольку f
a
(x
0
) = f
a
(−x
0
). Следовательно, для единствен-
ности решения необходимо, чтобы x
0
= 0 было решением задачи A (см.
68 Часть 1. Основные задачи и методы их решения
рис. 1.38, 1.39), и достаточно, чтобы решений (кроме x
0
= 0) боль-
ше не было (см. рис. 1.38), таким образом, случай, изображённый на
рис. 1.39, мы отбрасываем.
Решая задачу A, мы сначала будем:
1) находить возможные значения параметров из уравнения (нера-
венства) f
a
(0) = 0 (f
a
(0) 6 0), т. е. из не обходимого условия единствен-
ности;
2) для найденных значений параметров будем проверять, что дру-
гих решений (кроме x = 0) нет, т. е. проверять достаточное условие
единственности.
Пример 25 (психологический факультет, 1995, № 5). Найдите все
значения параметра a, при которых неравенство
cos x − 2
p
x
2
+ 9 6 −
x
2
+ 9
a + cos x
− a
имеет единственное решение.
Решение. Преобразуем неравенство к общему знаменателю:
cos x − 2
p
x
2
+ 9 6 −
x
2
+ 9
a + cos x
− a ⇐⇒
⇐⇒
(a + cos x)
2
− 2
√
x
2
+ 9(a + cos x) + x
2
+ 9
a + cos x
6 0 ⇐⇒
⇐⇒
(a + cos x −
√
x
2
+ 9)
2
a + cos x
6 0.
Обозначим
f(x) =
(a + cos x −
√
x
2
+ 9)
2
a + cos x
.
Поскольку функция f (x) чётная (f(x) = f(−x)), для того чтобы ис-
ходное неравенство f(x) 6 0 имело единственное решение, необходимо,
чтобы x = 0 было решением неравенства (если x
0
— решение неравен-
ства, то и −x
0
является решением в силу чётности функции f(x)).А
Таким образом, (a − 2)
2
/(a + 1) 6 0, т. е. a = 2 либо a < −1.
Проверим, является ли решение x = 0 исходного неравенства един-
ственным при найденных значениях параметра a.
Пусть a < −1. Тогда неравенство
(a + cos x −
√
x
2
+ 9)
2
a + cos x
6 0
§1.9. Задачи на единственность и количество решений 69
x
y
50
10
O
f(x)
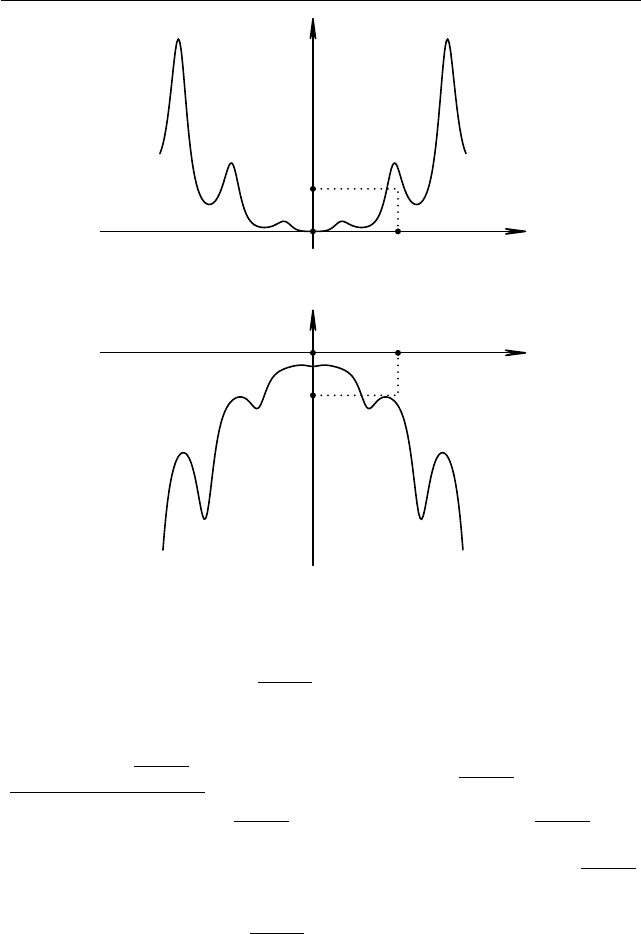
Рис. 1.40. График функции f (x) для a = 2
x
y
−50
10O
f(x)
Рис. 1.41. График функции f (x) для a = −2
выполнено для всех x ∈ R, так как для a < −1 справедливы
(a + cos x −
p
x
2
+ 9)
2
> 0, a + cos x < 0.
Пусть a = 2. Тогда 2 + cos x > 0 для любых x ∈ R. Следовательно,
(2 + cos x −
√
x
2
+ 9)
2
2 + cos x
6 0 ⇐⇒ (2 + cos x −
p
x
2
+ 9)
2
6 0 ⇐⇒
⇐⇒ 2 + cos x −
p
x
2
+ 9 = 0 ⇐⇒ 2 + cos x =
p
x
2
+ 9.
Но x = 0 является единственным корнем уравнения 2+cos x =
√
x
2
+ 9,
так как для x 6= 0 получаем неверное утверждение
3 <
p
x
2
+ 9 = 2 + cos x 6 3.
Ответ. a = 2.

70 Часть 1. Основные задачи и методы их решения
Задача 130 (физический факультет (май), 1999, № 7). При каких
значениях a уравнение cos 2x + 2 cos x − 2a
2
− 2a + 1 = 0 имеет ровно
одно решение на промежутке [0; 2π).
Задача 131 (факультет почвоведения (май), 2001, № 6). При каких
значениях параметра b уравнение tg |b| = log
2
(cos x − |x|) имеет ровно
один корень?
Задача 132 (механико-математический факультет, 1990, № 4).
Найдите все значения параметра a, при которых уравнение
x
2
− 2a sin(cos x) + a
2
= 0
имеет единственное решение.
Задача 133 (психологический факультет, 1995, № 5). Найдите все
значения параметра a, при которых неравенство
cos 2x + a 6 2
p
x
2
+ 16 −
x
2
+ 16
a + cos 2x
имеет единственное решение.
Задача 134 (московская школа экономики (июль), 2005, № 8 (8)).
Найдите все значения параметра b, при которых система уравнений
(
(x
2
+ 1)b = y + cos 2x,
2
|sin x|
+ |y| = 2
имеет единственное решение.
Задача 135 (механико-математический факультет, 1990, № 4).
Найдите все значения параметра b, при которых уравнение
b
2
x
2
− b tg(cos x) + 1 = 0
имеет единственное решение.
Задача 136 (факультет почвоведения, 1994, № 4). Найдите все
значения a и b, при которых система
(
a + sin bx 6 1,
x
2
+ ax + 1 6 0
имеет единственное решение.
