Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи
Подождите немного. Документ загружается.

§1.5. Уравнения, сводящиеся к исследованию квадратного 41
x
y
x
в
y
в
0
x
−
x
+
f(x)
x
y
x
в
y
в
0
x
−
x
+
f(x)
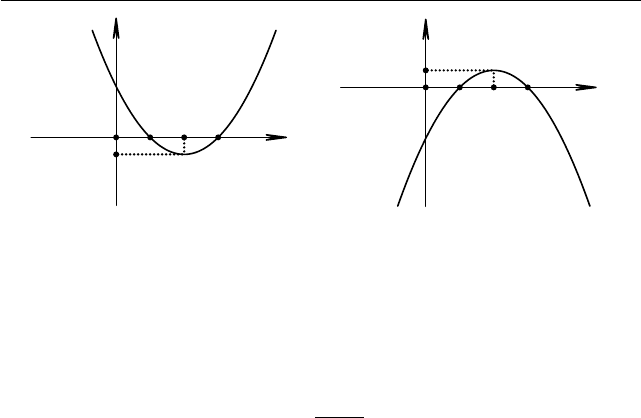
Рис. 1.22. D > 0, a > 0 Рис. 1.23. D > 0, a < 0
кой минимума. При a < 0 ветви пар аболы направл ены вниз, причём
абсцисса вершины параболы является точкой максимума.
Пример 15 (ЕГЭ (демо), 2005, № B6). При каких значениях a
функция
y =
2
ax+7
2
x
2
имеет максимум при x = 4?
Решение. Исходную функцию пред ставим в виде
y = 2
−x
2
+ax+7
.
Поскольку функция 2
t
монотонно возрастает, максимум функции
y = 2
−x
2
+ax+7
достигается в той же точке, что и у квадратичной функции
f(x) = −x
2
+ ax + 7.
У этой параболы ветви направлены вниз, следовательно, максимум
достигается в вершине параболы, т. е. в точке x
в
= a/2. Но согласно
условию x
в
= 4, следовательно, a = 8.
Ответ. a = 8.
Пример 16. При каждом з начении параметра a решите неравен-
ство
ax
2
+ x + 3a
3
> 0.
Решение. Пусть a = 0. Тогда решением неравенства буд ет мно-
жество чисел x > 0.
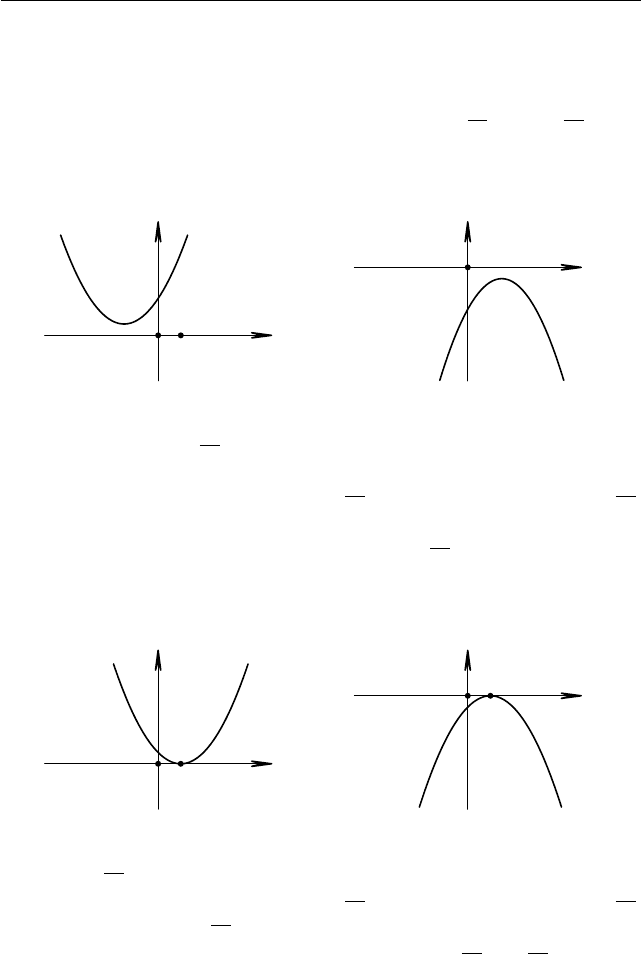
42 Часть 1. Основные задачи и методы их решения
При a 6= 0 функция f(x) = ax
2
+ x + 3a
3
— квадратный трёхчлен,
её график — парабола. Рассмотрим ещё три случая, в зависимости от
знака ди скр им инан та D = 1 − 12a
4
функции f(x), т. е. случаи D < 0,
D = 0, D > 0.
I. Пусть D = 1 − 12a
4
< 0, т. е. a ∈ (−∞; −1/
4
√
12) ∪ (1/
4
√
12; +∞).
Тогда в зависимости от знака a функция f(x) будет всюду положи-
тельна либо всюду отрицательна (см. рис. 1.24 и рис. 1.25). Для a > 0,
x
y
0
f(x)
1
x
y
0
f(x)
Рис. 1.24 Рис. 1.25
точнее, для a ∈ (1/
4
√
12; +∞), получаем f(x) > 0 для любого x ∈ R.
Для a < 0 получаем f(x) < 0 для любого x ∈ R.
Частичный ответ: при a 6 −1/
4
√
12 решений нет; если a > 1/
4
√
12,
то x ∈ (−∞; +∞).
II. Пусть D = 1 − 12a
4
= 0, т. е. a = ±1/
4
√
12. Тогда у квадратно-
го уравнения f(x) = 0 будет ед ин ственн ый корень x
0
= −1/2a (см .
рис. 1.26 и рис. 1.27). Для a > 0 получаем f(x) > 0 для любого
x
y
0
f(x)
x
0
x
y
0
f(x)
x
0
Рис. 1.26 Рис. 1.27
x ∈ R\{−
4
√
12/2}. Для a < 0 получаем f (x) 6 0 для любого x ∈ R.
Частичный ответ: при a = −1/
4
√
12 решений нет; если a = 1/
4
√
12,
то x ∈ (−∞; +∞)\{−
4
√
12/2}.
III. Пусть D = 1 − 12a
4
> 0, т. е. a ∈ (−1/
4
√
12; 1/
4
√
12). Тогда у
квадратного уравнения f(x) = 0 будет два решения (см. рис. 1.28 и
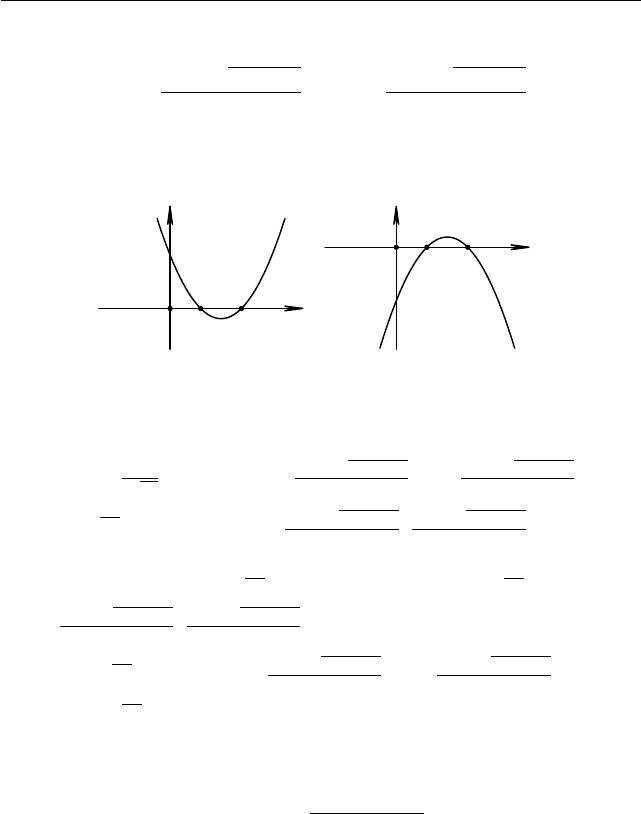
§1.5. Уравнения, сводящиеся к исследованию квадратного 43
рис. 1.29)
x
+
=
−1 +
√
1 − 12a
4
2a
, x
−
=
−1 −
√
1 − 12a
4
2a
.
Для a > 0 получаем f(x) > 0 для любого x ∈ (−∞; x
−
) ∪ (x
+
; +∞).
Для a < 0 получаем f(x) > 0 для любого x ∈ (x
+
; x
−
).
x
y
0
f(x)
x
−
x
+
x
y
0
f(x)
x
+
x
−
Рис. 1.28. Рис. 1.29.
Частичный ответ:
если 0 < a <
1
4
√
12
, то x ∈
−∞;
−1−
√
1−12a
4
2a
∪
−1+
√
1−12a
4
2a
; +∞
;
если −1/
4
√
12 < a < 0, то x ∈
−1+
√
1−12a
4
2a
;
−1−
√
1−12a
4
2a
.
Объединяя эти результаты, получаем ответ.
Ответ. При a 6 −1/
4
√
12 решений нет; если −1/
4
√
12 < a < 0, то
x ∈
−1+
√
1−12a
4
2a
;
−1−
√
1−12a
4
2a
; если a = 0, то x ∈ (0; +∞); если
0 < a 6 1 /
4
√
12, то x ∈
−∞;
−1−
√
1−12a
4
2a
∪
−1+
√
1−12a
4
2a
; +∞
;
если a > 1/
4
√
12, то x ∈ (−∞; +∞).
Пример 17 (экономический факультет (отделение менеджмента),
1995, № 6). Найдите все значения b, при которых уравнение
x − 2 =
p
2(b − 1)x + 1
имеет единственное решение.
Решение. Преобразуем уравнение:
(
x > 2,
(x − 2)
2
= 2(b − 1)x + 1
⇐⇒
(
x > 2,
x
2
− 2(b + 1)x + 3 = 0.
44 Часть 1. Основные задачи и методы их решения
У квадратной параболы f(x) = x
2
− 2(b + 1)x + 3 ветви направлены
вверх, поэтому единственное решение возможно лишь в следующих
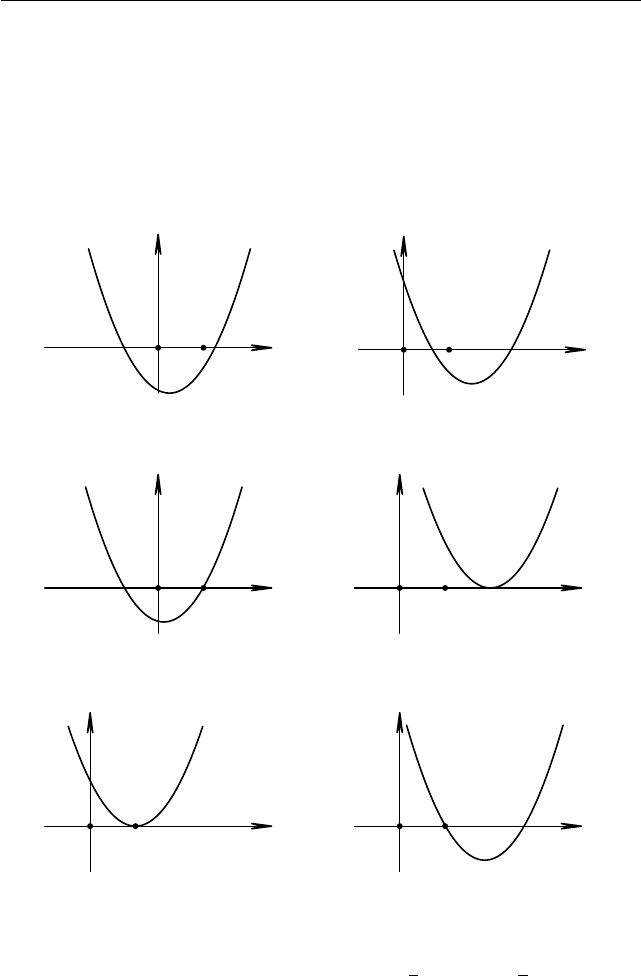
случаях (см. соответствующие рисунки 1.30–1.34):
I.
(
D > 0,
f(2) < 0;
II.
D > 0,
f(2) = 0,
x
в
< 2;
III.
(
D = 0,
x
в
> 2.
x
y
0
f(x)
2
x
y
0
f(x)
2
Рис. 1.30. Случай I Рис. 1.31. Случай I
x
y
0
f(x)
2
x
y
0
f(x)
2
Рис. 1.32. Случай II Рис. 1.33. Случай III
x
y
0
f(x)
2
x
y
0
f(x)
2
Рис. 1.34. Случай III Рис. 1.35. Случай двух корней
Найдем дискриминант уравнения f (x) = 0:
D = 4(b + 1)
2
− 4 · 3 = 4(b + 1 −
√
3)(b + 1 +
√
3).
§1.5. Уравнения, сводящиеся к исследованию квадратного 45
Разберём теперь каждый из перечисленных выше трёх случаев:
I.
(
D > 0,
f(2) < 0
⇐⇒
(
b ∈ (−∞; −1 −
√
3) ∪ (−1 +
√
3; +∞),
4 − 4(b + 1) + 3 < 0
⇐⇒
⇐⇒
(
b ∈ (−∞; −1 −
√
3) ∪ (−1 +
√
3; +∞),
b > 3/4.
Сравним числа −1 +
√
3 и 3/4:
−1 +
√
3 ∨ 3/4,
√
3 ∨ 7/4,
4
√
3 ∨ 7,
48 < 49.
Таким образом, решением в первом случае является множество всех
значений b > 3/4. Разберём второй случай. Вообще говоря, второй слу-
чай приходится разбирать отдельно от первого, поскольку возможна
ситуация (см. рис . 1.35), когда D > 0 и f(2) = 0, но при этом мы имеем
два решения (случай x
в
> 2).
II.
D > 0,
f(2) = 0,
x
в
< 2
⇐⇒
b ∈ (−∞; −1 −
√
3) ∪
∪ (−1 +
√
3; +∞),
b = 3 /4,
2(b + 1)
2
< 2
⇐⇒ b = 3/4.
Остаётся разобрать последний случай:
III.
(
D = 0,
x
в
> 2
⇐⇒
(
b = −1 ±
√
3,
b > 1
⇐⇒ b ∈ ∅.
Объединяя воедино все три случая, получаем ответ.
Ответ. b ∈ [3/4; +∞).
Задача 69 (ЕГЭ (демо), 2005, № B6). При каких значениях a функ-
ция
y =
3
x
2
3
ax−11
имеет минимум при x = 6?

46 Часть 1. Основные задачи и методы их решения
Задача 70 (ИСАА, 1998, № 7 (7)). При каких значениях параметра
a система
(
x
4
− (a − 1)
√
a + 3 y + a
4
+ 2a
3
− 9a
2
− 2a + 8 = 0,
y =
√
a + 3 x
2
имеет ровно три различных решения?
Задача 71 (московская школа экономики (июль), 2005, № 8 (8)).
При каких значениях параме тра a уравнение
(a − 1) · 4
x
+ (2a − 3) · 6
x
= (3a − 4) · 9
x
имеет единственное решение?
Задача 72 (механико-математический факультет (июль), 1993,
№ 2). Найдите все значения параметра a, при которых уравнение
4
x
+ (a
2
+ 5) · 2
x
+ 9 − a
2
= 0
не имеет решений.
Задача 73 (физический факультет (июль), 1994, № 7). Найдите
все значения a, дл я каждого из которых система
(
−x
2
+ 12x − a > 0,
x 6 2
выполняется хотя бы при одном значении x.
Задача 74 (физическ ий факультет (май), 1994, № 7). При каких
значениях a уравнение 2a(x + 1)
2
− |x + 1| + 1 = 0 имеет четыре раз-
личных корня?
Задача 75 (физический факультет (май), 1998, № 7). Найдите
все значения a, при которых неравенство log
1/5
(x
2
− ax + 7) < −1
выполняется для всех значений x из промежутка x < 0.
Задача 76 (экономический факультет (отделение менеджмента),
2005, № 6 (6)). Найдите все целые значения параметра a, при каждом
из которых все реше ния уравнения
3
√
x
6
−
1
a
− 2
·
4
√
x
4
+ 1 −
2
a
= 0
являются целыми числами.

§1.5. Уравнения, сводящиеся к исследованию квадратного 47
Задача 77 (психологический факультет, 1993, № 5). Обозначим
через x
1
и x
2
корни квадратного трёхчлена
(a − 1)x
2
− (2a + 1)x + 2 + 5a.
1. Найдите все значения параметра a, при которых x
1
> 1 и x
2
> 1.
2. Найдите все значения параметра b, для каждого из которых ве-
личина (x
1
−b)(x
2
−b) принимает постоянное значение при всех a, при
которых она определена.
Задача 78 (механико-математический факультет (июль), 2002,
№ 5). Найдите все значения параметра a, при каждом из которых сум-
ма арктангенсов корней уравнения x
2
+ (1 − 2a)x + a − 4 = 0 больше,
чем π/4.
Задача 79 (экономический факультет (отделение менеджмента),
1995, № 6). Найдите все значения p, при которых уравнение
x − 2 =
p
−2(p + 2)x + 2
имеет единственное решение.
Задача 80 (психологический факультет, 1989, № 5). При каждом
значении параметра a найдите все решения неравенства
x + 2a − 2
p
3ax + a
2
> 0.
Задача 81 (экономический факультет (отделение экономики)
(июль), 2003, № 6). Найдите все значения b, при которых уравнение
3 ·
5
√
x + 2 − 16b
2
·
5
√
32x + 32 =
10
p
x
2
+ 3x + 2
имеет единственное решение.
Задача 82 (географический факультет (май), 2002, № 6). Найдите
все значения параметра a, при каждом из которых уравнение
(a − 1) cos
2
x − (a
2
+ a − 2) cos x + 2a
2
− 4a + 2 = 0
имеет более одного решения на отрезке [0; 4π/3].
Задача 83 (биологический факультет и факультет фундаменталь-
ной медицины (июль), 2002, № 5). Найдите все значения параметра a,
при каждом из которых уравнени е
(x
2
+2(a−2)x+a
2
−4a)
2
+(a+5)(x
2
+2(a−2)x+a
2
−4a)−a
2
+8a+2 = 0
имеет: a) единственное решение; б) ровно два различных решения.

48 Часть 1. Основные задачи и методы их решения
Ответы. 69. a = 12. 70. a = 2. 71. a ∈ (−∞; 1] ∪ {5/4} ∪ [4/3, +∞).
72. |a| 6 3. 73. a ∈ (−∞; 20]. 74. a ∈ (0; 1/8). 75. a > −2
√
2 76. a = 2.
Указание. Квадратное уравнение должно иметь хотя бы один положи-
тельный корень. 77. 1. (1; (2 +
√
13)/4]; 2. b = 7/3. 78. a ∈ (2; +∞).
79. (−∞; −3/2]. 80. При a < 0 решений нет; если a = 0, то x ∈ (0; +∞);
если a > 0, то x ∈ [−a/3; 0), (8a; +∞). 81. b ∈ (−∞; −1/(2
√
2)]∪[−1/4; 1/4]∪
∪[1/(2
√
2); +∞). 82. a ∈ (−1/3; 3/10] ∪{1}. 83. а) 2 +
√
2, б) (−∞; 2 −
√
2) ∪
∪ {1} ∪ (2 +
√
2; +∞).
§1.6. Выделение полных квадратов
и неотрицательных выражений
При решении данных зад ач необходимо помнить формулы возве-
дения в квадрат для нескольких слагаемых:
(a + b)
2
= a
2
+ b
2
+ 2ab,
(a + b + c)
2
= a
2
+ b
2
+ c
2
+ 2ab + 2ac + 2bc,
(a + b + c + d)
2
= a
2
+ b
2
+ c
2
+ d
2
+ 2ab + 2ac + 2ad + 2bc + 2bd + 2cd.
Отсюда легко заметить (и доказать пр и помощи математической ин-
дукции), что при возведении в квадрат выражения a
1
+ a
2
+ . . . + a
n
в итоге получим сумму всех квадратов a
2
k
, k = 1, 2, . . . , n, и всех воз-
можных попарных произведений 2a
k
a
l
, 1 6 k < l 6 n, k, l ∈ Z, т. е
справедлива общая формула
(a
1
+ a
2
+ . . . + a
n
)
2
=
n
X
k=1
a
2
k
+ 2 ·
X
16k<l6n
a
k
a
l
.
Пример 18. Для каждого значения параметра a решите уравне-
ние
9a
2
+ log
2
2
x + 3 arccos(x − 1) − (3a − 1) log
2
x
2
− 6a + 1 = 0.
Решение. Преобразуем исходное уравнени е:
9a
2
+ log
2
2
x + 3 arccos(x − 1) − (3a − 1) log
2
x
2
− 6a + 1 = 0 ⇐⇒
⇐⇒ log
2
2
x − 2 · (3a − 1) log
2
x + 9a
2
− 6a + 1 + 3 arccos(x − 1) = 0 ⇐⇒
⇐⇒ log
2
2
x − 2 · (3a − 1) log
2
x + (3a − 1)
2
+ 3 arccos(x − 1) = 0 ⇐⇒
⇐⇒ (log
2
x − 3a + 1)
2
+ 3 arccos(x − 1) = 0.

§1.6. Выделение полных квадратов и неотрицательных выражений 49
Но поскольку функции (log
2
x−3a+1)
2
и 3 arccos(x−1) неотриц атель-
ные, исходное уравнение равносильно системе
(
log
2
x − 3a + 1 = 0,
3 arccos(x − 1) = 0
⇐⇒
(
a = 2/3,
x = 2.
Ответ. Если a = 2/3, то x = 2; при других a решений нет.
Пример 19 (биологический факультет, 1995, № 6). Найдите все
значения параметра a, при которых уравнение
(x
2
− 6|x| + a)
2
+ 10(x
2
− 6|x| + a) + 26 = cos(16π/a)
имеет ровно два корня.
Решение. Исходное уравнение равносильно следующему:
(x
2
− 6|x| + a)
2
+ 2 · 5(x
2
− 6|x| + a) + 25 + 1 − cos(16π/a) = 0 ⇐⇒
⇐⇒ (x
2
− 6|x| + a + 5)
2
+ (1 − cos(16π/a)) = 0.
Функции (x
2
−6|x|+a+5)
2
и 1−cos(16π/a) неотрицательные, и сходное
уравнение равносильно системе
(
x
2
− 6|x| + a + 5 = 0,
1 − cos(16π/a) = 0
⇐⇒
(
(|x| − 3)
2
= 4 − a,
a = 8/n, n ∈ Z
⇐⇒
⇐⇒
a 6 4,
|x| = 3 ±
√
4 − a,
a = 8/n, n ∈ Z.
Уравнение |x| = 3 ±
√
4 − a имеет ровно два корня, только если
√
4 − a = 0, либо 3 −
√
4 − a < 0, т. е. либо a = 4, либо a < −5. Сле-
довательно, значения параметра a дол жны принадлежать множеству
(−∞; −5) ∪ {4}. Отсюда с учётом равенства
a = 8/n, n ∈ Z ⇐⇒ a = ±8, ±4, ±8/3, . . .
находим два значения параметра a = 4, a = −8, принадлежащие мно-
жеству (−∞; −5) ∪ {4}.
Ответ. При a = 4, a = −8.
50 Часть 1. Основные задачи и методы их решения
Задача 84 (факультет почвоведе ния (май), 1995, № 5). Найдите
все значения параметра a, при которых уравнение
2 cos 2x − 4a cos x + a
2
+ 2 = 0
не имеет решений.
Задача 85 (ИСАА, 1994, № 6). Найдите все значения параметра a,
при каждом из которых уравнени е
a
2
x
2
+ 2a(
√
2 − 1)x +
√
x − 2 = 2
√
2 − 3,
имеет решение.
Задача 86 (физический факультет (март), 1999, № 5 (8)). Решите
систему уравнений
(
√
x
2
+ 3x + 2 − |y + 2| = 0,
2
p
y
2
+ 4y + 4 +
√
x
2
− x − 2 = 0.
Задача 87 (химический факультет (июль), 1995, № 5). Решите
систему
(
2
−x
y
4
− 2y
2
+ 2
x
6 0,
8
x
− y
4
+ 2
x
− 1 = 0 .
Задача 88 (филологический факультет, 1978, № 2). Число α по-
добрано так, что уравнение
q
x −
√
3 + α
2
x
2
+ 2αx(
√
6 −
√
3) = 6
√
2 − 9
имеет решение. Найдите это решение.
Задача 89 (психологический факультет, 1979, № 5). Найдите все
тройки целых чисел (x; y; z), для которых выполняется соотношение
5x
2
+ y
2
+ 3z
2
− 2yz = 30.
Задача 90 (биологический факультет, 1995, № 6). Найдите все
значения параметра a, при которых уравнение
(x
2
− 6|x| − a)
2
+ 12(x
2
− 6|x| − a) + 37 = cos(18π/a)
имеет ровно два решения.
