Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи
Подождите немного. Документ загружается.

§1.1. Простейшие уравнения и неравенства с параметром 11
Решение. Преобразуем это неравенство:
a
x + a
− 1 > 0 ⇐⇒
a − x − a
x + a
> 0 ⇐⇒
⇐⇒
−x
x + a
> 0 ⇐⇒
x
x + a
< 0.
Решение вполне аналогично р еше нию примера 3. Именно, располо-
жим на оси точки −a и 0. Возможны 3 случая.
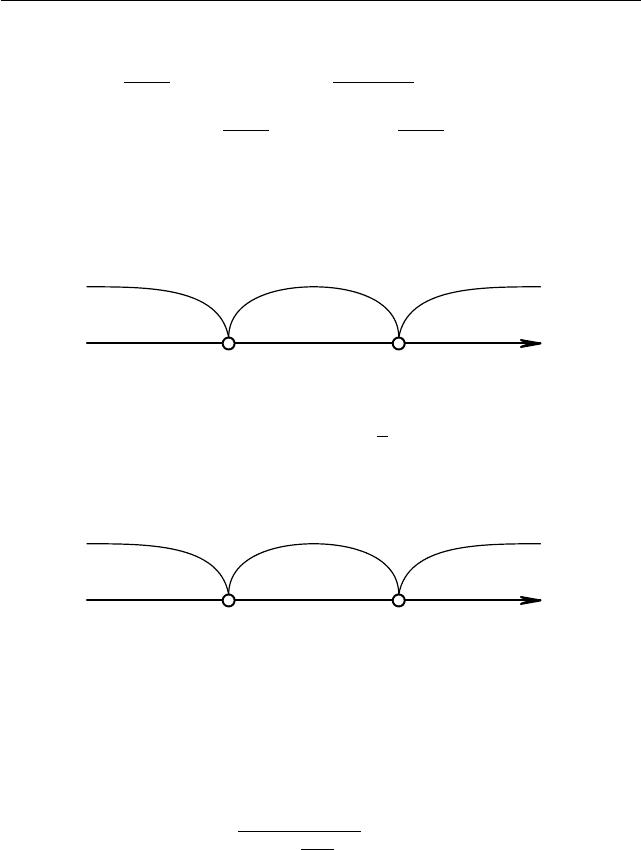
I. Пусть a > 0, тогда −a < 0 и точки располагаются, как показано
на рис. 1.4. Мы получаем решение x ∈ (−a; 0).
+ − +
−a
0
x
Рис. 1.4
II. Пусть a = 0, тогда мы получаем
x
x
< 0, или 1 < 0 при x 6= 0.
Это неравенство не имеет решений.
III. Наконец, если a < 0, то число −a > 0 и точки располагаются,
как показано на рис. 1.5. Отсюда следует, что x ∈ (0; −a).
+ − +
0
−a
x
Рис. 1.5
Объединяя части ответа, получаем окончательный результат.
Ответ. Если a < 0, то x ∈ (0; −a); если a = 0, то x ∈ ∅; если a > 0,
то x ∈ (−a; 0).
Пример 6. При всех a решите неравенство
(x − 1)(x − a)
x −
a+1
2
> 0.
Решение. Заметим, что при любом фиксированном значении a это
обычное рациональное неравенство, для решения которого применим
метод интервалов. Однако при попытке непосредственного использо-
вания этого метода мы сталкиваемся с трудностью, состоящей в том,
что нам неизвестно, как располагаются точки 1, a, (a + 1)/2 на оси.
12 Часть 1. Основные задачи и методы их решения
Как обойти трудность такого сорта? Рассмотрим возможные различ-
ные случаи. Для этого попарно сравним числа 1 и a, 1 и (a + 1)/2, a и
(a + 1)/2. Находим
a ∨ 1, (a + 1)/2 ∨ 1, a ∨ (a + 1)/2,
a ∨ 1, a + 1 ∨ 2, 2a ∨ a + 1,
a ∨ 1, a ∨ 1, a ∨ 1.
Откуда получаем, что при a < 1 выполнено двойное неравенство
a <
a + 1
2
< 1,
при a = 1 получаем, что все числа 1, a и (a + 1)/2 равны. При a > 1
выполнено двойное неравенство
1 <
a + 1
2
< a.
Следовательно, разберём три случая.
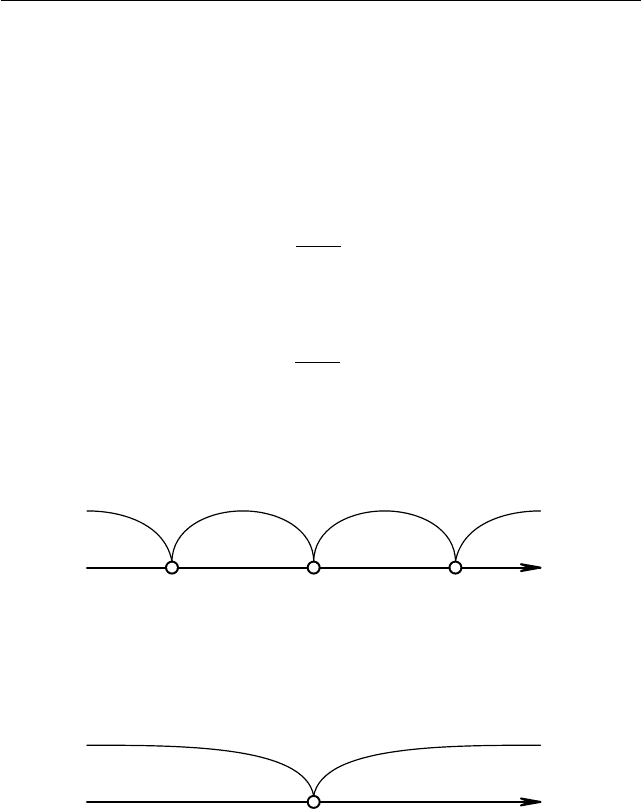
I. Пусть a < 1. Тогда 1 > (a + 1)/2 > a. Применим метод ин-
тервалов (см. рис. 1.6). Получаем частичный ответ: если a < 1, то
x ∈ (a; (a + 1)/2) ∪ (1; +∞).
− + − +
a
(a + 1)/2
1
x
Рис. 1.6
II. Пусть a = 1. Тогда a = (a + 1)/2 = 1. Применим метод ин-
тервалов (см. рис. 1.7). Получаем частичный ответ: если a = 1, то
x ∈ (1; +∞).
− +
1
x
Рис. 1.7
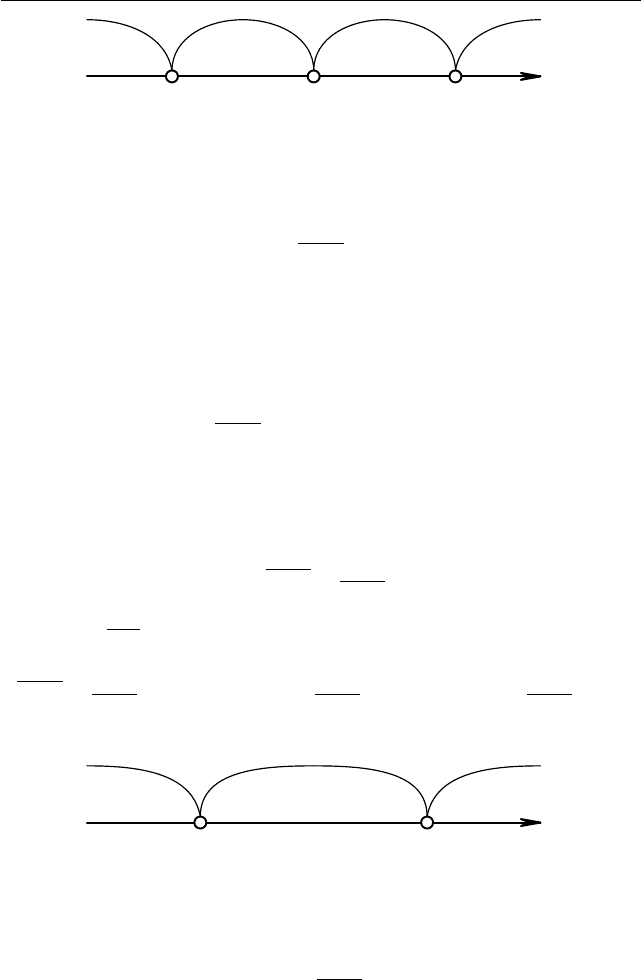
III. Пусть a > 1. Тогда a > (a + 1)/2 > 1. Применим метод ин-
тервалов (см. рис. 1.8). Получаем частичный ответ: если a < 1, то
x ∈ (1; (a + 1)/2) ∪ (a; +∞).
Ответ. Если a < 1, то x ∈ (a; (a + 1)/2) ∪ (1; +∞); если a = 1, то
x ∈ (1; +∞); если a < 1, то x ∈ (1; (a + 1)/2) ∪ (a; +∞).
§1.1. Простейшие уравнения и неравенства с параметром 13
− + − +
1
(a + 1)/2
a x
Рис. 1.8
Пример 7 (физический факультет (июль), 1997, № 7). Для любых
значений a решите неравенство
(a + 4)
√
5 − x > a + 3.
Решение. Найдём область допустимых значений (ОДЗ): 5−x > 0.
Следующий шаг — преобразование неравенства. Нам будет удобно раз-
делить обе части на число a+4. Но при этом возможны случаи a+4 < 0,
a + 4 > 0 и a + 4 = 0.
I. Пусть a + 4 = 0, тогда
0 ·
√
5 − x > −1 ⇐⇒ 0 > −1.
Последнее неравенство справедливо во всей ОДЗ. Получаем частич-
ный ответ: если a = −4, то x 6 5.
II. Пусть a + 4 < 0, тогда и сходное неравенство равносильно сле-
дующему:
√
5 − x <
a + 3
a + 4
.
Поскольку
a+3
a+4
> 0 при a < −4 (см. рис. 1.9), мы получаем
√
5 − x <
a + 3
a + 4
⇐⇒ 5 − x <
a + 3
a + 4
2
⇐⇒ 5 −
a + 3
a + 4
2
< x.
+ − +
−4 −3
a
Рис. 1.9
С учётом ОДЗ получаем частичный ответ: если a < −4, то
x ∈
5 −
a + 3
a + 4
2
; 5
.
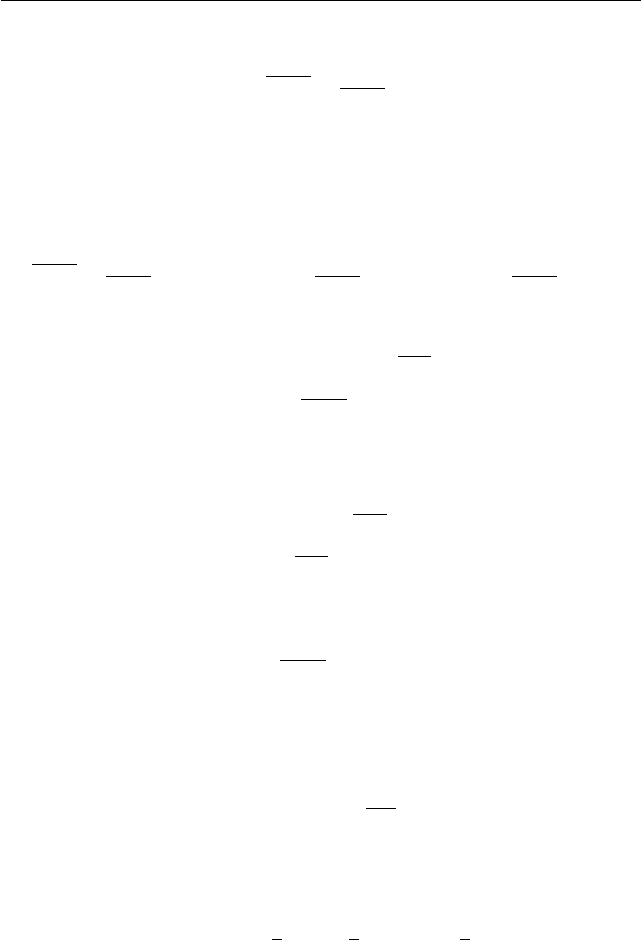
14 Часть 1. Основные задачи и методы их решения
III. Пусть a + 4 > 0, тогда исходное неравенство равносильно сле-
дующему:
√
5 − x >
a + 3
a + 4
.
Поскольку выражение (a + 3)/(a + 4) (см. рис. 1.9) отрицательно при
a ∈ (−4; −3), равно нулю при a = −3 и положительно пр и a > −3,
рассмотрим несколько случаев.
III a. Пусть a > −3. Тогда (см. рис. 1.9) (a + 3)/(a + 4) > 0 и,
следовательно, можем преобразовать исходное неравенство:
√
5 − x >
a + 3
a + 4
⇐⇒ 5 −x >
a + 3
a + 4
2
⇐⇒ 5 −
a + 3
a + 4
2
> x.
Все полученные значения входят в ОДЗ. Следовательно, получаем ча-
стичный ответ: если a > −3, то x < 5 −
a+3
a+4
2
.
III b. Пусть a ∈ (−4; −3). Тогда (см . ри с. 1.9) (a + 3)/(a + 4) < 0
и, следовательно, неравенство
√
5 − x > (a + 3)/(a + 4) выполнено на
всей области допустимых значений. Получаем частичный ответ: если
a ∈ (−4; −3), то x 6 5.
Остаётся собрать все полученные результаты в ответ.
Ответ. Если a < −4, то x ∈
5 −
a+3
a+4
2
; 5
i
; если a ∈ [−4; −3), то
x 6 5; если a > −3, то x < 5 −
a+3
a+4
2
.
Задача 1 (химический факультет (июль), 2003, № 1). Найдите все
значения параметра a, при которых множество решений неравенства
a
x − a
> 0
содержит точку x = 1.
Задача 2 (ЕГЭ, 2003, № B4). При каком наименьшем положитель-
ном значении b функция
y = sin
20x +
bπ
150
имеет минимум в точке x
0
= π/2?
Задача 3 (факультет ВМиК (июль), 2002, № 1). При каких значе-
ниях параметра b уравнение
b
4
x + b
2
+ (2 +
√
2)b + 2
√
2 = b
2
(b +
√
2) + 4x
имеет бесконечно много корней?

§1.1. Простейшие уравнения и неравенства с параметром 15
Задача 4 (физический факультет (март), 1997, № 7). Найдите все
значения a, при которых неравенство log
a
(x
2
+2) > 1 выполняется для
всех значений x.
Задача 5 (психологический факультет, 1994, № 2). Известно, что
x = 1, y = −1 — одно из решений системы
2ax + by =
√
3 tg
1111π
6
,
ax
2
+ by
2
= 2.
Найдите все решения данной системы.
Задача 6 (хими чес ки й факультет (май), 2003, № 1). Найдите все
значения параметра a, при которых уравнение
ax
2
+ (a + 1)x + 1 = 0
имеет единственное решение.
Задача 7 (факультет ВМиК (отделение бакалавров) (июль), 2003,
№ 4 (7)). При всех значениях параметра c решите уравнен ие
4
x
+ c · 25
x
= 3 · 10
x
.
Задача 8 (факультет почвоведения (июль), 1999, № 7). Для каж-
дого значения параметра b 6 0 решите неравенство (относительно x)
√
x
2
− 1
x
> b.
Задача 9 (физический факультет (июль), 1999, № 7). Для любо-
го допустимого значения a решите неравенство log
2a
(log
3
x
2
) > 1 и
найдите, при каком значении a множество точек x, не являющихся ре-
шением неравенства, представляет собой промежуток, длина которого
равна 6?
Задача 10 (факультет почвоведения (июль), 1997, № 6). Для каж-
дого значения параметра c решите неравенство
√
c
2
− x
2
> 2 − c.
Задача 11 (физический факультет (июль), 1997, № 7). Для любых
значений a решите неравенство a − 2 < (a − 1)
√
x + 1.
Задача 12 (факультет почвоведения (июль), 2005, № 5 (6)). Для
каких значений параметра p отношение суммы коэффициентов много-
члена (px
2
− 7)
18
к его свободному члену минимально?
16 Часть 1. Основные задачи и методы их решения
Задача 13 (физический факультет (м ай), 2003, № 7). Для каждого
допустимого значения b решите неравенство
p
7 + log
b
x
2
+ (log
b
|x|)(1 + 2 log
x
b) > 0.
Задача 14 (филологический факультет (апрель), 2002, № 6). Для
каждого значения параметра a решите уравнение
p
|x| + 1 −
p
|x| = a.
Задача 15 (физический факультет (июль), 2002, № 7). Для каж-
дого значения a решите неравенство log
1/9
(x
2
−6x −a
2
−5a + 12) < −1
и найд ите, при каких значениях a множество точек x, не являющихся
решениями этого неравенства, представляет собой отрезок числовой
оси, длина которого меньше 2
√
3.
Задача 16 («Покори Воробьёвы горы» (апрель)
1
, 2006, № 6 (6)).
При всех значениях параметра a решите уравнение
2
ax+3
x
2
+3
+ 2
4x
2
−ax+9
x
2
+3
= 10.
Задача 17 (географический факультет (май), 2000, № 2). Найдите
все значения параметра a, при каждом из которых уравнение
log
a−6,5
(x
2
+ 1) = log
a−6,5
(a − 5)x
имеет два различных решения.
Задача 18 (факультет почвоведения (июль), 2002, № 7). Найдите
все значения a, пр и каждом из которых уравнение
(x
3
− 1)(x
2
− 16)
lg(15a − x) − lg(x − a)
= 0
имеет единственное решение.
Задача 19 (физический факультет (июль), 2000, № 7). При каких
значениях p уравнение
4(x −
p
p · 7
p
)x + p + 7(7
p
− 1) = 0
имеет корни и каковы знаки корней при различных значениях p?
Задача 20 (физический факультет (март), 2000, № 7). При каких
значениях b уравнение
25
x
− (2b + 5)5
x−1/x
+ 10b · 5
−2/x
= 0
имеет ровно два решения.
1
Этот вариант писали на следующих факультетах: химическом, биологическом,
географическом, почвоведения, наук о материалах и психологическом.

§1.1. Простейшие уравнения и неравенства с параметром 17
Задача 21 (ЕГЭ (демо), 2004, № С4). Найдите все значения пара-
метра a, при которых множество решений неравенства
x(x − 2) 6 (a + 1)(|x − 1| − 1)
содержит все члены н екоторой бесконечно убывающей геометрической
прогрессии с первым членом, равным 1,7, и положительным знамена-
телем.
Задача 22 (геологический факультет (май), 2000, № 7). Найдите
все значения a, при которых каждое решение неравенства x
2
+ a 6 0
удовлетворяет неравенству (x + 2a)
√
3 − x 6 0.
Задача 23 (химический факультет, 1987, № 5). Найдите все значе-
ния параметра p, при каждом из которых множество решений неравен-
ства (p−x
2
)(p+x−2) < 0 не содержит ни одного решения неравенства
x
2
6 1.
Задача 24 (геологический факультет (май), 1995, № 7). Пусть
f(x) =
p
x
2
− 4x + 4 − 3, g(x) =
√
x − a,
где a — параметр. Решите относительно x неравенство f (g(x)) 6 0.
Задача 25 (ИСАА (июль), 2001, № 6). Найдите все значения па-
раметра a, при каждом из которых система уравнений
(
x + a(y + 1) = 2a,
x
3
+ a(2y
3
+ 1) = ay
3
+ 2a
имеет не более двух решений.
Задача 26 (механико-математический факультет (май), 2002, № 4).
Найдите все значения параметра a, при каждом из которых уравнение
log
a+1
x + log
x
(19 − 8a) = 2
имеет по крайней мере два корня и при этом произведение всех его
корней не менее 0,01.
Задача 27 (психологический факультет, 1992, № 4). Найдите все
значения параметров a и b, при которых найдутся два различных
корня уравнения x
3
− 5x
2
+ 7x = a, которые будут также корнями
уравнения x
3
− 8x + b = 0.
18 Часть 1. Основные задачи и методы их решения
Задача 28 (механико-матем атиче ски й факультет, 1985, № 4). Из
трёх значений a: −1,2; −0,67; −0,66 найдите все те значения, при каж-
дом из которых уравнение
2
a+4
+ 15(x + a)
1 + 2 cos
π
a +
x
2
= 0
имеет хотя бы одно решение, удовлетворяющие условию 0 6 x 6 1.
Задача 29 (филологический факул ьтет, 2000, № 5 (6)). Найдите
все a, при каждом из которых уравнения
(2a − 1)x
2
+ 6ax + 1 = 0 и ax
2
− x + 1 = 0
имеют общий корень.
Задача 30 (психологический факультет, 1990, № 5). Считая из-
вестным, что при любом a > 0 уравнение 2x
3
+ x
2
−x −a −1 = 0 имеет
единственный положительный корень x
0
(зависящий от a), найдите
все a > 0, при которых 12x
3
0
− 7x
0
> 6a + 1.
Ответы. 1. a ∈ (0; 1). 2. b = 125. 3. b = −
√
2. 4. a ∈ (1; 2).
5. (1; −1), (−1/5; 7/5). 6. a = 0; 1. 7. c ∈ [1; 5/2) ∪ [4; +∞). 8. Если b 6 −1,
то x ∈ (−∞; −1] ∪ [1; +∞); если −1 < b 6 0, то x ∈ (−1/
√
1 − b
2
; −1] ∪
∪ [1; +∞). 9. 1. Если a ∈ (0; 1/2), то x ∈ (−3
a
; −1) ∪ (1; 3
a
); если a > 1/2, то
x ∈ (−∞; −3
a
) ∪ (3
a
; +∞). 2. При a = 1. 10. При c ∈ (−∞; 1) решений нет;
если c ∈ [1; 2), то x ∈ [−2
√
c − 1; 2
√
c − 1]; если c ∈ [2; +∞) то x ∈ [−c; c].
11. Если a < 1, то x ∈ [−1;
“
a−2
a−1
”
2
− 1); если a ∈ [1; 2), то x > −1;
если a > 2, то x >
“
a−2
a−1
”
2
− 1. 12. p = 7. Указание. Сумма коэф-
фициентов любого многочлена равна его значению в точке 1. 13. Если
b ∈ (0; 1), то x ∈ (0; 1) ∪ (1; b
−3
); если b ∈ (1; +∞), то x ∈ (b
−3
; 1) ∪ (1; +∞).
14. Если a ∈ (0; 1], то x = ±((1 − a
2
)/2a)
2
; при других a решений нет.
15. 1. Если a ∈ (−3; −2), то x ∈ R; если a ∈ (−∞; −2] ∪ [−3; +∞), то
x ∈ (−∞; 3−
√
a
2
+ 5a + 6)∪(3+
√
a
2
+ 5a + 6; +∞). 2. a ∈ ((−5−
√
13)/2; −3]∪
∪ [−2; (−5 +
√
13)/2). 16. x = 0, a при любом a, x = (a ±
√
a
2
− 72)/6 при
|a| > 6
√
2. 17. a ∈ (7; 7,5) ∪ (7,5; +∞). 18. a ∈ (1/15; 1/8) ∪ (1/8; 4/15] ∪
∪ {1/2} ∪ [1; 4). 19. При p = 0 один корень x = 0, при p = 7 один корень
x = 7
4
/2, при p > 7 два положительных корня. 20. b ∈ (0; 1/50)∪(25/2; +∞).
21. (−∞; 0,7]. 22. a = 0, a ∈ [−9; −1/4]. 23. p ∈ (−∞; 0] ∪ [3; +∞).
24. Если a ∈ (−∞; −5), то решений нет; если a = −5, то x = 0; если
a ∈ (−5; 1), то x ∈ [0; (a + 5)
2
]; если a ∈ [1; +∞), то x ∈ [(a − 1)
2
; (a + 5)
2
].
25. a ∈ {−1}∪[−1/2; 0)∪(0; 1/2]∪{1}. 26. a ∈ [−9/10; 0)∪(2; 9/4)∪(9/4; 19/8).
27. a = 2, b = 3. 28. a = −1,2; a = −0,67. 29. a = −3/4, a = 0, a = 2/9.
30. a ∈ (0; 1/54).

§1.2. Простейшие задачи с модулем 19
§1.2. Простейшие задачи с модулем
A. В задачах с модулем п олезн ы неравенства
|x + y| 6 |x| + |y|, |x|− |y| 6 |x − y|, x, y ∈ R.
Пример 8. При всех a решите неравенство
|x + a| > a.
Решение. Как и в предыдущем параграфе, отметим, что при за-
мене параметра a на произвольное число получается вполне стандарт-
ная задача. Поэтому можно применить метод интервалов для модулей.
Сначала отметим, что при a < 0 это неравенство, очевидно, верное
(так как модуль числа — неотрицате льная величина) при любом a.
Поэтому получаем часть ответа: если a < 0, то x ∈ (−∞; +∞).
Если a = 0, то |x| > 0 и x ∈ (−∞; 0) ∪ (0; +∞).
Если a > 0, то следует рассмотреть два случая: x < −a и x > −a.
В первом из них исходное неравенс тво равносильно след ующему:
−x − a > a ⇐⇒ − x > 2a ⇐⇒ x < −2a.
Так как a > 0, число −2a меньше, чем −a. Поэтому
x ∈ (−∞; −2a) ⊂ (−∞; −a),
и пересечение этих областей совпадает с (−∞; −2a).
Во втором случае, т. е. при x + a > 0, получаем x + a > a, x > 0,
x ∈ (0; +∞). Так как −a < 0, множество [−a; +∞) содержит множество
(0; +∞), и их пересечение р авно (0; +∞). Поэтому при a > 0 решением
неравенства будет (−∞; −2a) ∪ (0; +∞).
Объединим части ответа: если a < 0, то x ∈ (−∞; +∞); если a = 0,
то x ∈ (−∞; 0) ∪ (0; +∞); если a > 0, то x ∈ (−∞; −2a) ∪ (0; +∞).
Заметим, что если a = 0, то −2a = 0, поэтому последние две части
ответа можно объединить так: если a > 0, то x ∈ (−∞; −2a) ∪(0; +∞).
Ответ. Если a < 0, то x ∈ (−∞; +∞); если a > 0, то x ∈ (−∞; −2a)∪
∪ (0; +∞).
Пример 9. При всех a решите неравенство
|x + a| < x.
Решение. Как и в предыдущей задаче, рассмотрим два случая.

20 Часть 1. Основные задачи и методы их решения
I. Пусть x + a < 0. Тогда получаем
−x − a < x ⇐⇒ 2x > −a ⇐⇒ x > −a/2.
Рассматриваемая область задана условием x < −a. Часть ответа мо-
жет быть получена как решение системы неравенств
(
x > −a/2,
x < −a.
Если a > 0, то число −a меньше, чем −a/2, и эта система не имеет
решений.
Если a = 0, то получаем систему
(
x > 0,
x < 0,
очевидно, не имеющую решений.
Если a < 0, то −a > −a/2, и мы получаем x ∈ (−a/2; −a).
Итак, часть ответа в первом случае: если a < 0, то x ∈ (−a/2; −a);
если a > 0, то x ∈ ∅.
II. Пусть x + a > 0. Тогда получаем неравенство x + a < x, a < 0,
которое верно при a < 0 в рассматриваемой области, т. е. при x > −a,
или x ∈ [−a; +∞). При a > 0 это неверное неравенство, не имеющее
решений.
Часть ответа: если a < 0, то x ∈ [−a; +∞); если a > 0, то x ∈ ∅.
Объединяя части ответа, получаем: если a < 0, то x ∈ (−a/2; −a) ∪
∪ [−a; +∞) = (−a/2; +∞); если a > 0, то x ∈ ∅.
Ответ. Если a < 0, то x ∈ (−a/2; −a) ∪ [−a; +∞) = (−a/2; +∞);
если a > 0, то x ∈ ∅.
Пример 10 (химический факультет, 1992, № 5). Найдите все зна-
чения параметра a, при которых уравнение
5|x − 3a| + |x − a
2
| + 4x = a
1) имеет бесконечное множество решений, 2) не имеет решений.
Решение. Исходное уравнение можно заменить совокупностью че-
тырёх систем:
1)
5(x − 3a) + (x − a
2
) + 4x = a,
x > 3a,
x > a
2
;
2)
5(3a − x) + (x − a
2
) + 4x = a,
x 6 3a,
x > a
2
;
