Ковалев В.В., Волкова О.Н. Анализ хозяйственной деятельности предприятия
Подождите немного. Документ загружается.


Этот метод позволяет сравнивать объемы товарооборота двух периодов и судить о "реальном"
изменении этой величины, независимом от изменившихся цен. Таким образом, при анализе показателей
в условиях изменяющихся цен, когда требуется устранять влияние этого фактора, следует
руководствоваться следующим правилом: пересчету подвергается отчетное значение показателя путем
его деления на индекс цен.
Мы привели здесь лишь самые общие формулировки аналитических задач, решаемых с помощью
индексного метода. На самом же деле этот метод является одним из самых мощных, информативных и
распространенных инструментов экономического анализа во всех его аспектах: от анализа деятельности
отдельных хозяйствующих единиц до макроэкономических исследований национальных экономик.
Вдумчивого читателя, интересующегося этими проблемами, можно отослать как к классическим
учебникам общей статистики, так и к специальным монографиям.
2.8. Математико-статистические методы изучения связей
Математико-статистические методы изучения связей, называемые иначе стохастическим
моделированием, являются в определенной степени дополнением и углублением детерминированного
анализа. В анализе финансово-хозяйственной деятельности стохастические модели используются, когда
необходимо:
оценить влияние факторов, по которым нельзя построить жестко детерминированную модель;
изучить и сравнить влияние факторов, которые невозможно включить в одну и ту же
детерминированную модель;
выделить и оценить влияние сложных факторов, которые не могут быть выражены одним
определенным количественным показателем.
В отличие от детерминистского, стохастический подход для своей реализации требует выполнения
ряда предпосылок. В первую очередь речь идет о наличии достаточно большой совокупности объектов
(жестко детерминированную модель можно анализировать и строить по одному объекту, для
стохастической же модели необходима совокупность). Кроме того, необходим достаточный объем
наблюдений: по одному-двум наблюдениям судить о характере стохастической связи нельзя.
Использование стохастических моделей в экономике, в отличие от использования их в технике, имеет
определенные трудности, связанные с получением совокупности достаточного объема. В технике
эксперимент можно повторить, в экономике этого сделать нельзя. Это приводит к дискуссии о
правомерности использования статистических методов при построении факторных моделей в анализе
деятельности предприятий, поскольку при этом нередко приходится работать в условиях малых выборок
(менее 20 наблюдений), а кроме того, в теории статистики считается, что при построении регрессии
количество наблюдений должно в 6-8 раз превышать количество факторов, что крайне редко встречается
в анализе финансово-хозяйственной деятельности предприятий.
Поскольку стохастическая модель - это, как правило, уравнение регрессии, при ее построении
должны выполняться следующие условия:
случайность наблюдений;
наличие однородности совокупности, как качественной, так и количественной (показателем
количественной однородности совокупности данных является показатель вариации, который мы
рассмотрели в разделе 2.7.3);
наличие специального математического аппарата (например, инструменты анализа автокорреляций
для анализа рядов динамики).
Основная сфера приложения стохастических моделей — это проблемно-ориентированный и
тематический анализ. Стохастическое моделирование предназначено для решения трех основных задач:
установление самого факта наличия (или отсутствия) статистически значимой связи между
изучаемыми признаками;
прогнозирование неизвестных значений результативных показателей по заданным значениям
факторных признаков (задачи экстраполяции и интерполяции);
61

выявление причинных связей между изучаемыми показателями, измерение их тесноты и
сравнительный анализ степени влияния.
Проведение стохастического моделирования - сложный процесс, состоящий из нескольких этапов, на
каждом из которых выполняются определенные процедуры.
Этап 1 - качественный анализ. Он включает:
постановку цели анализа;
определение совокупности включаемых в анализ данных;
определение результативных признаков;
определение факторных признаков;
выбор периода анализа;
выбор метода анализа.
Этап 2 - предварительный анализ моделируемой совокупности, что подразумевает:
проверку однородности совокупности;
исключение аномальных наблюдений;
уточнение необходимого объема выборки;
установление законов распределения изучаемых переменных.
Этап 3 - построение регрессионной модели экономического объекта, которое включает:
перебор конкурирующих вариантов моделей;
уточнение перечня факторов, включаемых в модель;
расчет оценок параметров уравнений регрессии.
Этап 4 - оценка адекватности модели, которая заключается в следующем:
проверка статистической значимости уравнения в целом и его отдельных параметров;
проверка соответствия формальных свойств полученных оценок задачам исследования.
Этап 5 - экономическая интерпретация и практическое использование модели. Под этим понимается:
определение пространственно-временной устойчивости зависимостей;
оценка прогностических свойств моделей.
Рассмотрим некоторые аспекты осуществления процедур стохастического анализа.
Во-первых, для анализа следует брать всю имеющуюся совокупность данных. Если она слишком
велика, следует внимательно отнестись к составлению выборки из этой совокупности. Выборка должна
быть типичной для данного круга явлений. В противном случае анализ не будет иметь смысла,
поскольку его результаты не позволят делать значимые выводы для всей совокупности.
Во-вторых, в качестве результативных признаков берут либо показатели эффекта (выручка,
товарооборот, объем реализации), либо показатели эффективности (рентабельность, оборачиваемость и
т.п.). Отметим, что в анализе более предпочтительным является использование относительных
показателей. Причин тому несколько, в качестве основных можно назвать их сравнимость и большую
близость их распределений нормальному закону (это весьма важно, поскольку нормальность
распределения признаков - основная предпосылка корреляционно-регрессионного анализа, речь о
котором пойдет далее).
В-третьих, в качестве факторных признаков следует брать показатели, комплексно характеризующие
изучаемое явление. При этом также лучше ориентироваться на относительные показатели.
В-четвертых, существует два подхода к анализу явлений: статический и динамический. Статический
подход встречается чаще, поскольку проведение его проще и не требует использования сложных
математических методик. Динамический анализ (анализ рядов данных во времени) нередко
предполагает рассмотрение автокорреляционных зависимостей, что требует от аналитика владения
сложным эконометрическим инструментарием.
В-пятых, предварительная обработка рядов данных начинается с установления законов
распределения: распределение данных должно быть близко к нормальному. В условиях малых выборок
проверка нормальности распределений признаков проводится путем сравнения эмпирических
коэффициентов асимметрии и эксцесса (их аналитические выражения приведены в разделе 2.7.3) с их
средними квадратическими ошибками (σ
As
и σ
Ex
, соответственно). Нормальность распределения
подтверждается, если выполнены неравенства: |As| < 3σ
As
и |Ех| < 3σ
Ex
.
В-шестых, проверка однородности сводится к проверке соотношения Vаr
33%, где Var -
коэффициент вариации (см. раздел 2.7.3). Если совокупность неоднородна, следует исключить из нее
самые "аномальные" наблюдения, поскольку они, скорее всего, нетипичны для данного исследования.
Для устранения аномальных наблюдений используется правило "трех сигм": наблюдение признается
62
аномальным и отбрасывается, если его отклонение от выборочной средней (x
i
—) более чем в 3 раза
превышает среднеквадратическое отклонение выборки σ. Безусловно, любые операции с исходной
совокупностью, в том числе и связанные с изменением ее объема, должны быть обоснованными и
поясняемыми.
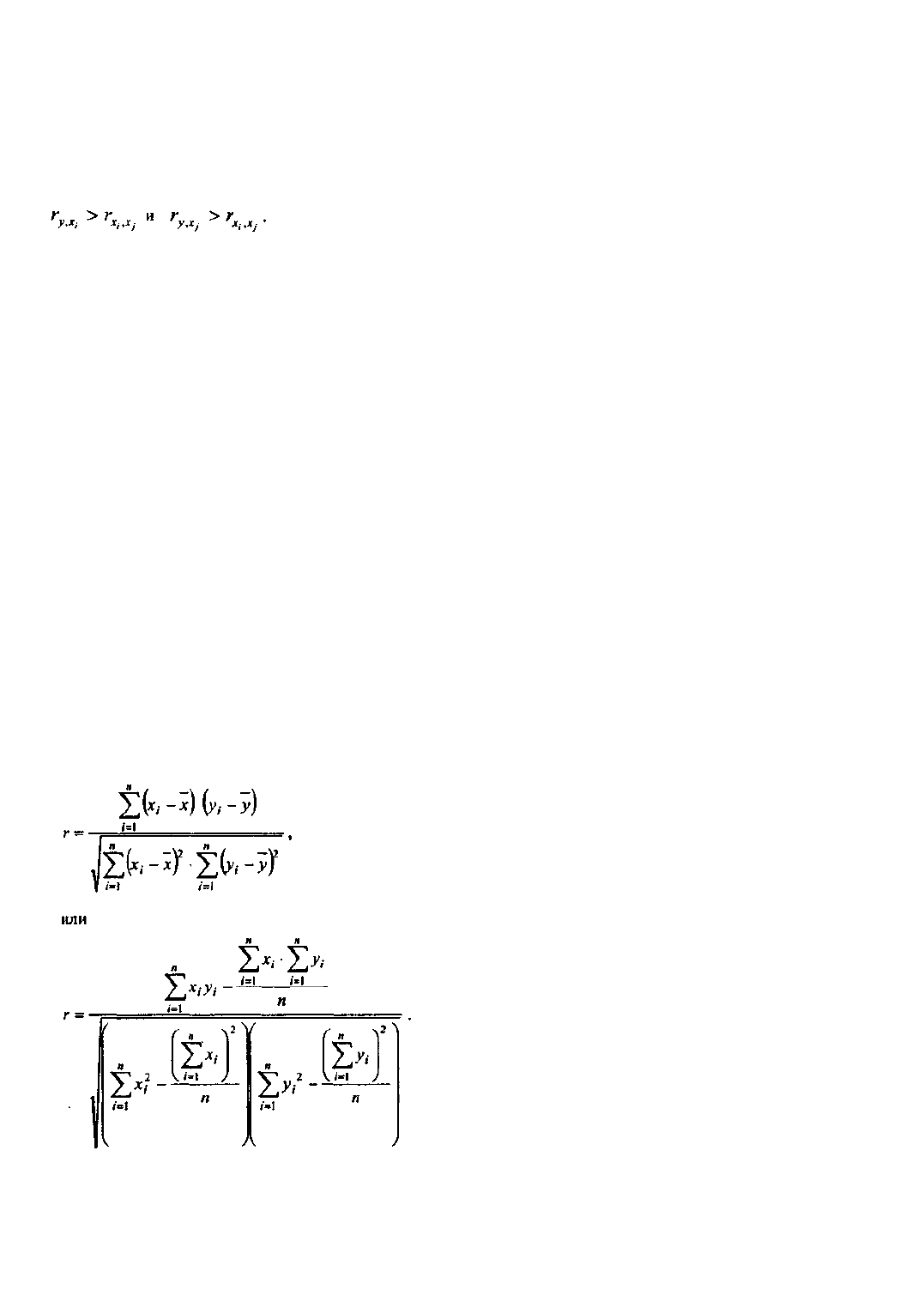
В-седьмых, уточнение перечня факторов может осуществляться, например, путем расчета матрицы
парных коэффициентов корреляции. Факторы x
i
и x
j
включаются в модель вида y = f(x
1,
x
2
, .....х
п
)
одновременно, если:
Перебор конкурирующих вариантов моделей, как правило, осуществляется с использованием
компьютера.
В-восьмых, проверка устойчивости модели осуществляется расчетом ее параметров на усеченной или
расширенной совокупности, а также по той же совокупности, но в другом временном интервале.
2.8.1. Корреляционный анализ
Корреляционный анализ есть метод установления связи и измерения ее тесноты между
наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной
по многомерному нормальному закону.
Корреляционной связью называется такая статистическая связь, при которой различным значениям
одной переменной соответствуют разные средние значения другой. Возникать корреляционная связь
может несколькими путями. Важнейший из них - причинная зависимость вариации результативного
признака от изменения факторного. Кроме того, такой вид связи может наблюдаться между двумя
следствиями одной причины. Основной особенностью корреляционного анализа следует признать то,
что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая ее причин.
В статистике теснота связи может определяться с помощью различных коэффициентов (Фехнера,
Пирсона, коэффициента ассоциации и т.д.), а в анализе хозяйственной деятельности чаще используется
линейный коэффициент корреляции.
Коэффициент корреляции между факторами x и у определяется следующим образом:
Таким же образом вычисляется коэффициент корреляции между факторами в двухфакторной
регрессионной модели вида у = ах + b, a также при любой другой форме связи между двумя
показателями.
Значения коэффициента корреляции изменяются в интервале [-1; + 1]. Значение r = -1
свидетельствует о наличии жестко детерминированной обратно пропорциональной связи между
63
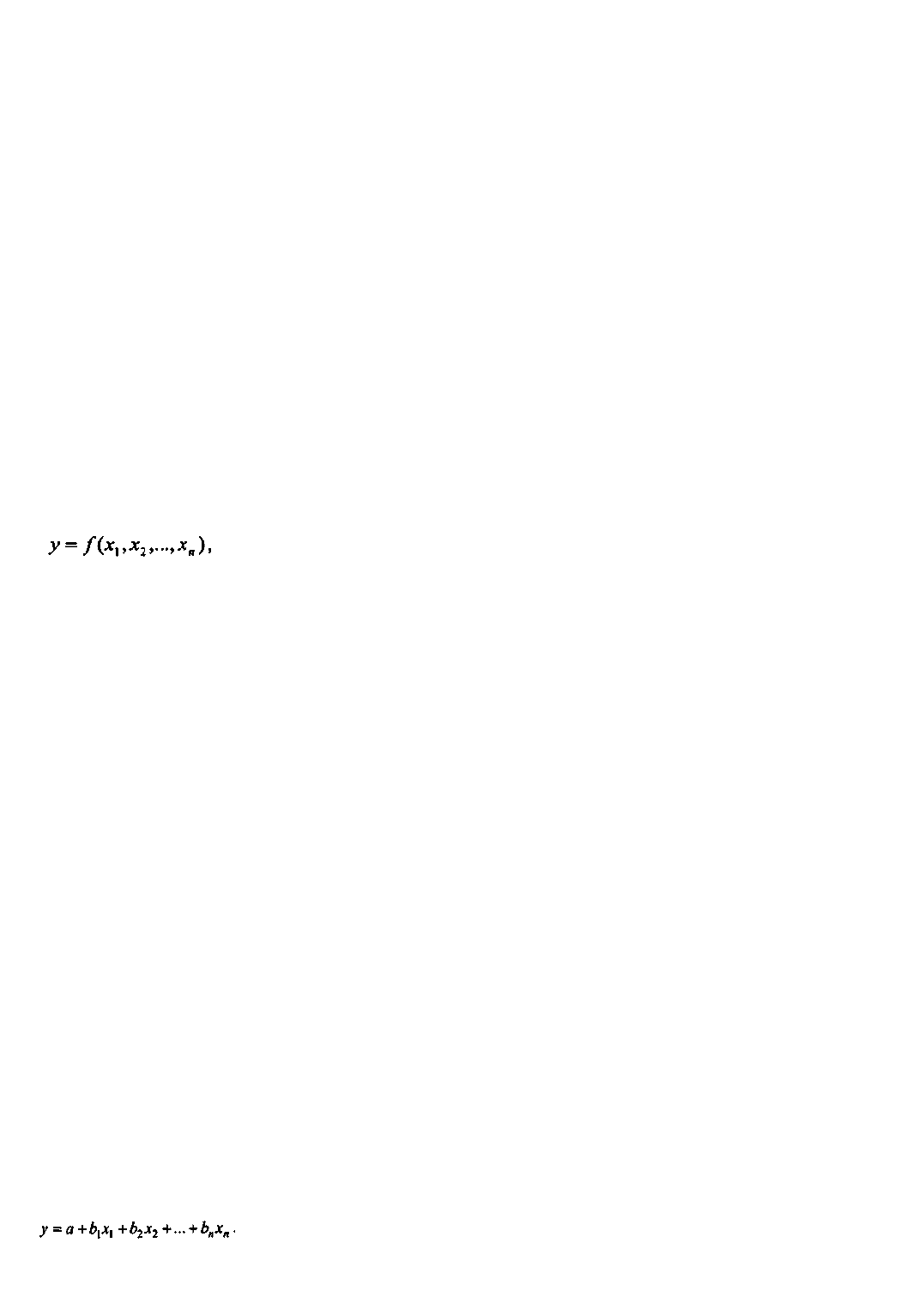
факторами, r = +1 соответствует жестко детерминированной связи с прямо пропорциональной
зависимостью факторов. Если линейной связи между факторами не наблюдается, r
0. Другие
значения коэффициента корреляции свидетельствуют о наличии стохастической связи, причем чем
ближе |r| к единице, тем связь теснее.
При |r|<0,3 связь можно считать слабой; при 0,3 < |r| < 0,7 - связь средней тесноты; |r| > 0,7 - тесная.
Существуют и более дробные градации (например, таблица Чэддока).
Практическая реализация корреляционного анализа включает следующие этапы:
а) постановка задачи и выбор признаков;
б) сбор информации и ее первичная обработка (группировки, исключение аномальных наблюдений,
проверка нормальности одномерного распределения);
в) предварительная характеристика взаимосвязей (аналитические группировки, графики);
г) устранение мультиколлинеарности (взаимозависимости факторов) и уточнение набора показателей
путем расчета парных коэффициентов корреляции;
д) исследование факторной зависимости и проверка ее значимости;
е) оценка результатов анализа и подготовка рекомендаций по их практическому использованию.
2.8.2. Регрессионный анализ
Регрессионный анализ - это метод установления аналитического выражения стохастической
зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем
изменяется у при изменении любого из x
i
, и имеет вид:
где у - зависимая переменная (она всегда одна);
х
i
- независимые переменные (факторы) (их может быть несколько).
Если независимая переменная одна - это простой регрессионный анализ. Если же их несколько (п
2), то такой анализ называется многофакторным.
В ходе регрессионного анализа решаются две основные задачи:
построение уравнения регрессии, т.е. нахождение вида зависимости между результатным
показателем и независимыми факторами x
1
, x
2
, …, x
n
.
оценка значимости полученного уравнения, т.е. определение того, насколько выбранные
факторные признаки объясняют вариацию признака у.
Применяется регрессионный анализ главным образом для планирования, а также для разработки
нормативной базы.
В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь
между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение.
Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный -
одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных
признаков влияет на признак результативный.
Регрессионный анализ - один из наиболее разработанных методов математической статистики.
Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных
требований (в частности, x
l
,x
2
,...,x
n
; y должны быть независимыми, нормально распределенными
случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие
требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода
весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не
только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при
наличии любой зависимости, однако в многофакторном анализе используют только линейные модели
вида:
Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов, суть
64
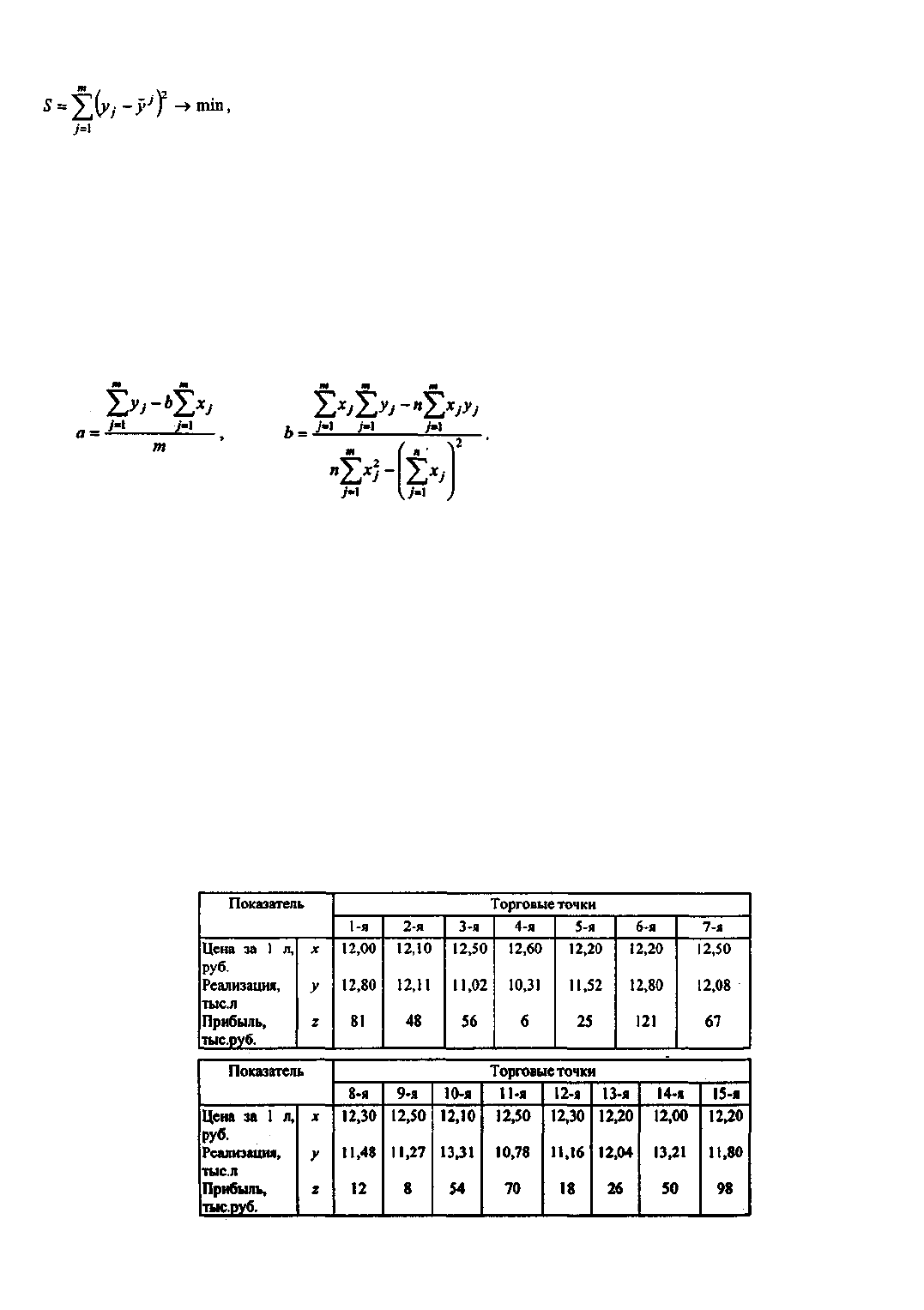
которого состоит в минимизации суммы квадратов отклонений фактических значений результатного
признака от его расчетных значений, т.е.:
где т - число наблюдений;
y
j
= a + b
1
x
1
j
+ b
2
x
2
j
+ ... + b
n
х
n
j
- расчетное значение результатного фактора.
Коэффициенты регрессии рекомендуется определять с помощью аналитических пакетов для
персонального компьютера или специального финансового калькулятора. В наиболее простом случае
коэффициенты регрессии однофакторного линейного уравнения регрессии вида y = а + bх можно найти
по формулам:
Рассмотрим использование методов корреляционного и регрессионного анализа на примере 2.13.
Пример 2.13. Наибольшим спросом в торговых точках города, реализующих молочную продукцию, пользуется
молоко "Лето", выпускаемое в пакетах объемом 1 литр. Цены за единицу этого товара в разных торговых точках
города варьируют.
Известно, что реализация этого продукта вносит существенный вклад в общую выручку торговых точек.
Возможно, она влияет и на величину прибыли предприятий торговли. Так ли это - позволит установить анализ.
1. По данным, касающимся цен на упаковку молока "Лето" и объемов реализации в 15 торговых точках
города, построим уравнение регрессионной зависимости между этими факторами.
2. Методом регрессионного анализа определим, есть ли связь между величиной чистой прибыли предприятий
торговли и объемами реализации ими молока "Лето", если для всех 15 анализируемых точек известны величины
прибыли за II квартал 1999 г., а также цены и объемы реализации данной марки молока (табл. 2.5).
Таблица 2.5
Показатели деятельности торговых предприятий, реализующих молоко "Лето", за II квартал 1999 г.
Анализ будем проводить с помощью табличного процессора MS Excel. Описательная статистика для
представленных данных отражена в табл. 2.6.
65

Таблица 2.6
Описательная статистика реализации молока "Лето" торговыми точками
1. Анализ следует начать с проверки однородности совокупности данных. Критерием однородности является
условие:
Var < 0,33.
Видим, что это условие выполняется лишь для рядов данных, относящихся к ценам (фактор x) и объемам
реализации (фактор у) молока.
Проверка нормальности распределений этих факторов показывает:
Условия нормальности выполняются, следовательно, по двум этим рядам данных можно строить
регрессионную зависимость.
Следующим шагом при построении регрессионной модели будет определение результативного и факторного
признаков. Исходя из сути поставленной задачи, можно сказать, что в данном случае независимым фактором
является цена за литр, объем реализации - признак зависимый (результатный).
Регрессионная зависимость между факторами х и у (зависимость объема реализации молока от его цены) будет
иметь вид:
Полученный результат - обратно пропорциональная зависимость между факторами - вполне согласуется со
здравым смыслом: очевидно, что чем выше цена, тем менее привлекательна торговая точка для покупателей
данного товара.
Регрессионная зависимость позволяет строить прогноз величины результативного фактора при известной
величине зависимого (т.е. прогноз объема реализации от цены за литр молока).
Подставив, например, х = 12,40 руб. за литр в аналитическую формулу зависимости, получим ожидаемое
значение объема реализации за квартал - y = 11,72 тыс. литров.
2. Определить, связан ли объем прибыли, полученной предприятиями торговли, с объемами реализации ими
одного вида продукции, можно с помощью корреляционного анализа. Матрица корреляций, рассчитанная с
помощью компьютера, выглядит так:
Величины коэффициентов парной корреляции факторов таковы:
Эти величины свидетельствуют о том, что между ценой товара (х) и объемом его реализации (у) связь весьма
тесная (величина 0,82 говорит о том, что 82% вариации фактора у объясняются вариацией фактора х). Прибыль
предприятия от цены на этот товар зависит слабо (коэффициент корреляции равен -0,32), а вот связь величины
66
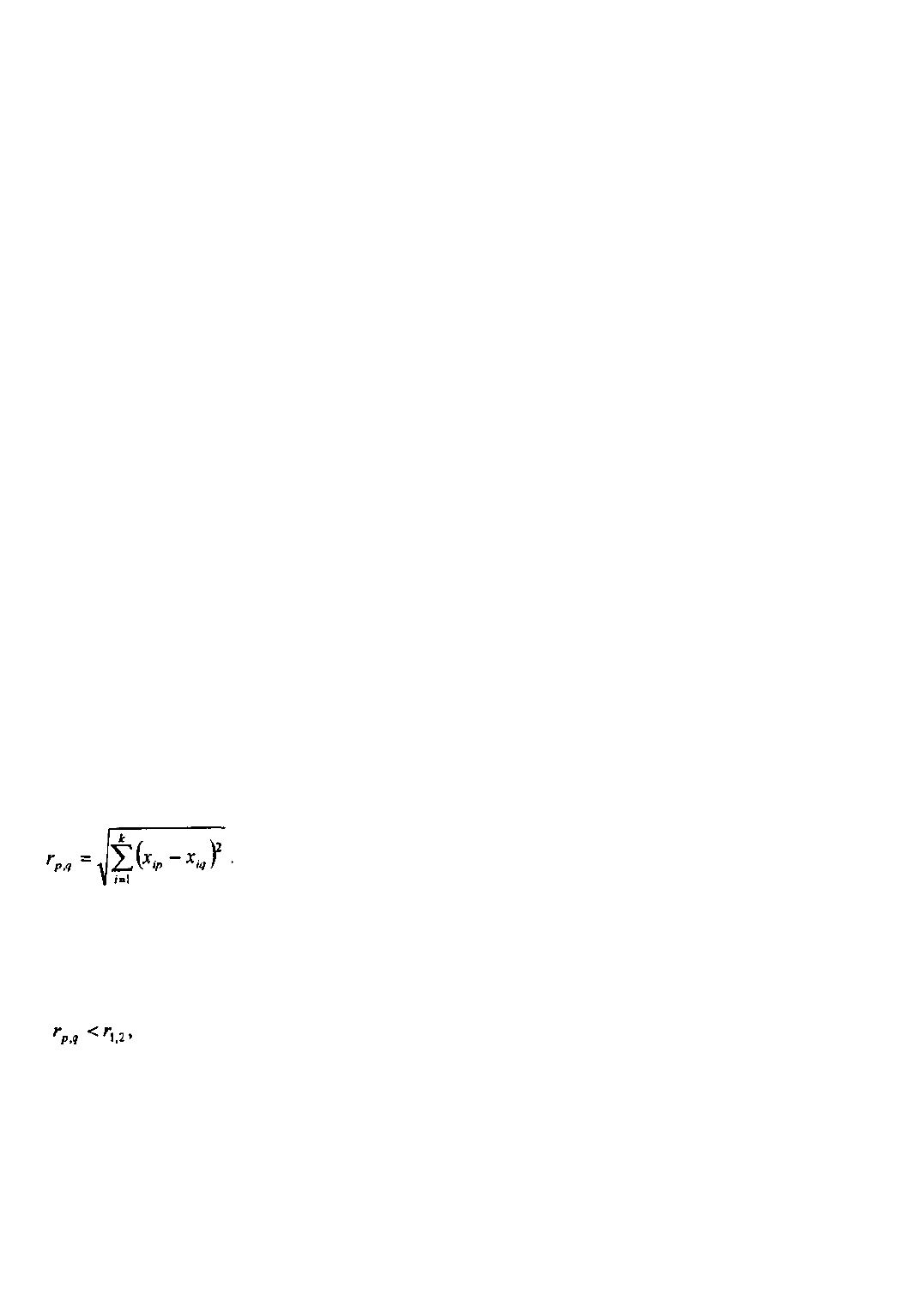
прибыли и объемов реализации молока "Лето" оказалась средней силы (r
yz
= 0,49), причем зависимость прямо
пропорциональная.
Следовательно, увеличение объемов реализации этого товара в среднем довольно заметно влияет на рост
прибыли предприятий торговли. По результатам анализа руководству магазинов следует подумать о мерах по
стимулированию продажи молока этой марки.
Можно ли построить и регрессионную зависимость прибыли от исследуемых факторов?
Для полного ряда из 15 значений критерий однородности (Vаr < 0,33) не выполняется, следовательно,
использовать полный ряд значений прибыли нельзя. Лишь исключив по четыре наибольших и наименьших
значения, можно привести этот ряд к однородности. Проверка нормальности для усеченной совокупности данных
(по 7 оставшимся магазинам) показывает, что все три ряда значений нормальны. Правда, при этом вызывает
сомнение правомочность использования статистических процедур на столь малой выборке. Однако если
отвлечься от этого факта, то и в этом случае зависимость вида z = а + b
1
х + b
2
у не даст аналитику значимой
информации, поскольку между факторами х и у наблюдается сильная взаимозависимость (мультиколлинеарность)
- об этом свидетельствует высокое значение парного коэффициента корреляции (на усеченной выборке r
xy
= -
0,88).
Поэтому при регрессионном анализе прибыли целесообразно брать лишь один из этих факторов, а именно
объем реализации, поскольку его связь с величиной прибыли более тесная (r
yz
= 0,78, тогда как r
xz
= 0,48 - также
по усеченной выборке).
Необходимо отметить, что в экономических исследованиях корреляционный и регрессионный
анализы нередко объединяются в один - корреляционно-регрессионный анализ. Подразумевается, что в
результате такого анализа будет построена регрессионная зависимость (т.е. проведен регрессионный
анализ) и рассчитаны коэффициенты ее тесноты и значимости (т.е. проведен корреляционный анализ). В
известном смысле корреляционная связь носит более общий характер, поскольку она не предполагает
наличия зависимости "причина - следствие".
2.8.3. Кластерный анализ
Кластерный анализ - один из методов многомерного анализа, предназначенный для группировки
(кластеризации) совокупности, элементы которой характеризуются многими признаками. Значения
каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном
пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей,
можно представить как точку в пространстве этих показателей, значения которых рассматриваются как
координаты в многомерном пространстве. Расстояние между точками р и q с k координатами
определяется как:
Основным критерием кластеризации является то, что различия между кластерами должны быть более
существенны, чем между наблюдениями, отнесенными к одному кластеру, т.е. в многомерном
пространстве должно соблюдаться неравенство:
где r
1,2
- расстояние между кластерами 1 и 2.
Так же как и процедуры регрессионного анализа, процедура кластеризации достаточно трудоемка, ее
целесообразно выполнять на компьютере.
2.8.4. Дисперсионный анализ
Дисперсионный анализ - это статистический метод, позволяющий подтвердить или опровергнуть
гипотезу о том, что две выборки данных относятся к одной генеральной совокупности. Применительно
к анализу деятельности предприятия можно сказать, что дисперсионный анализ позволяет определить, к
одной и той же совокупности данных или нет относятся группы разных наблюдений.
67
Дисперсионный анализ часто используется совместно с методами группировки. Задача его
проведения в этих случаях состоит в оценке существенности различий между группами. Для этого
определяют групповые дисперсии σ
1
2
и σ
2
2
, а затем по статистическим критериям Стьюдента или
Фишера проверяют значимость различий между группами.
2.9. Методы теории принятия решений
2.9.1. Метод построения дерева решений
Этот метод входит в систему методов ситуационного анализа и используется в случаях, когда
прогнозируемая ситуация может быть структурирована таким образом, что выделяются ключевые
моменты, в которых либо нужно принимать решение с определенной вероятностью (роль аналитика или
менеджера активна), либо также с определенной вероятностью наступает некоторое событие (роль
аналитика или менеджера пассивна, однако значимы некоторые не зависящие от его действий
обстоятельства). Именно для формализованного описания подобных ситуаций и используется так
называемый метод построения дерева решений. Логику метода рассмотрим на примере 2.14.
Пример 2.14. Управляющему нужно принять решение о целесообразности приобретения либо станка М1, либо
станка М2. Станок М2 более экономичен, что обеспечивает больший доход на единицу продукции, вместе с тем
он более дорогой и требует относительно больших накладных расходов.
Процесс принятия решения может быть выполнен в несколько этапов.
Этап 1 - определение цели. В качестве критерия выбирается максимизация математического ожидания
прибыли.
Этап 2 - определение набора возможных действий для рассмотрения и анализа (контролируются лицом,
принимающим решение).
Управляющий может выбрать один из двух вариантов:
a
1
= {покупка станка М1} либо
a
2
= {покупка станка М2}
Этап 3 - оценка возможных исходов и их вероятностей (носят случайный характер). Управляющий оценивает
возможные варианты годового спроса на продукцию и соответствующие им вероятности следующим образом:
x
1
= 1200 единиц с вероятностью 0,4;
x
2
= 2000 единиц с вероятностью 0,6,
P(x
1
) = 0,4; p(x
2
) = 0,6.
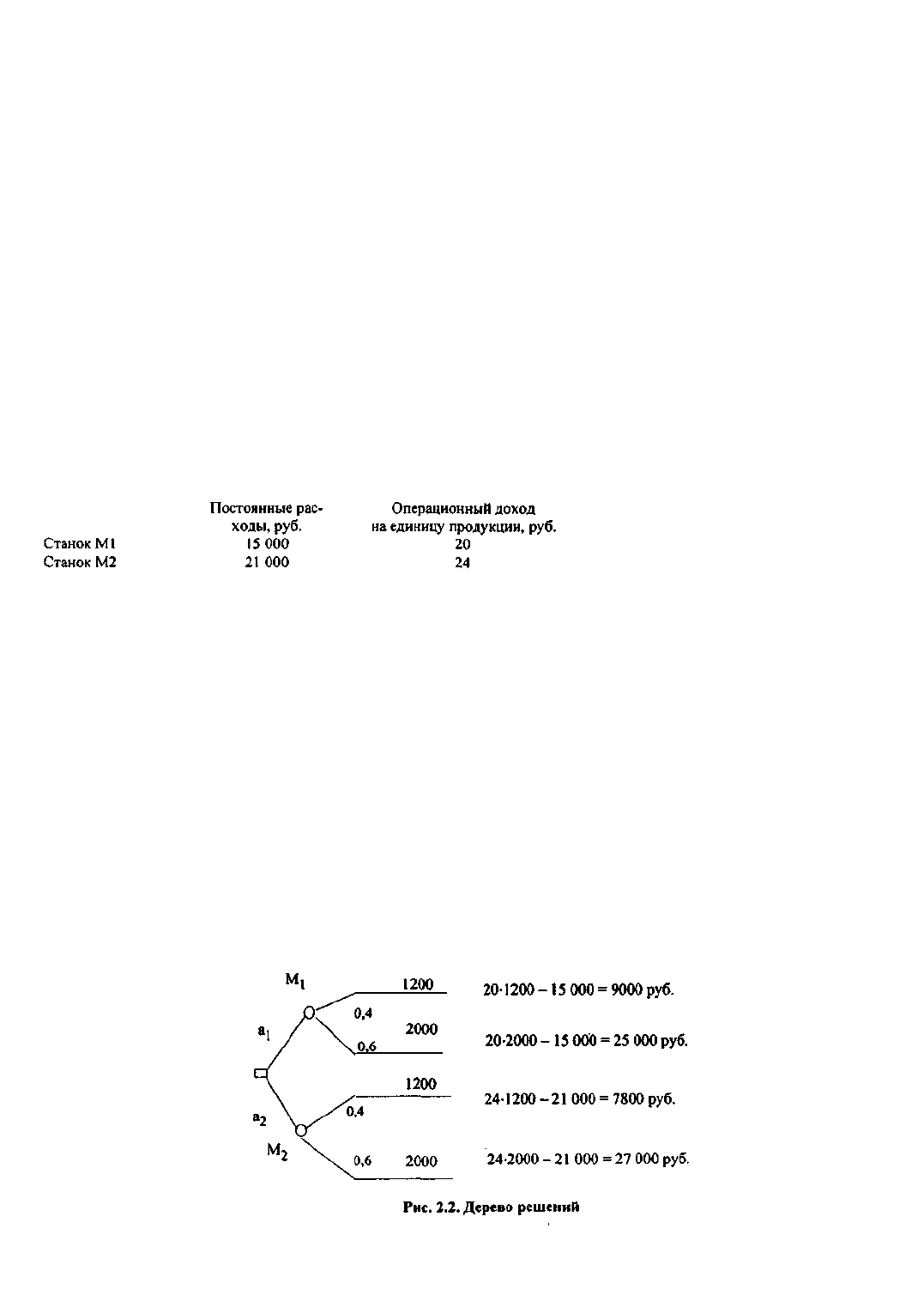
Этап 4 - оценка математического ожидания возможного дохода. Выполняется с помощью дерева решений
(рис. 2.2).
Из приведенных на схеме данных можно найти математическое ожидание возможного исхода по каждому
проекту:
68
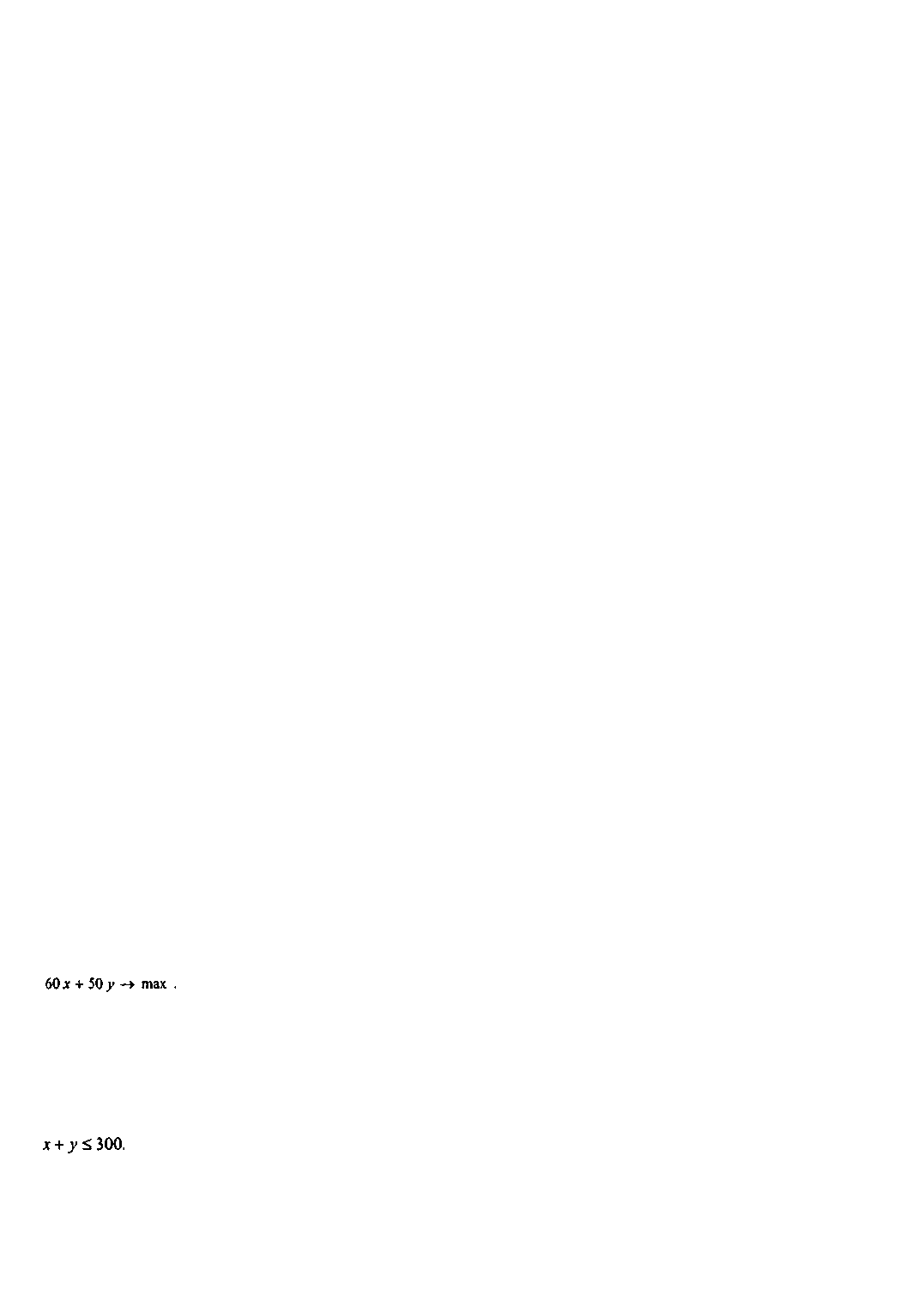
E(R
a1
) = 9000 ∙ 0,4 + 25 000 ∙ 0,6 = 18 600 руб.
E(R
a2
)
=
7800 ∙ 0,4 + 27 000 ∙ 0,6 = 19 320 руб.
Таким образом, вариант с приобретением станка М2 является экономически более целесообразным.
Мы рассмотрели наиболее общие подходы к формализации процесса прогнозирования возможных
действий, основанные на построении дерева решений. Этот метод весьма полезен в различных областях
деятельности менеджеров, например, в управленческом учете, при составлении бюджета
капиталовложений и особенно в анализе на рынке ценных бумаг. Более подробно с возможностями этого
метода как в теоретическом, так и в практическом аспектах можно ознакомиться по имеющейся
оригинальной и переводной литературе (см., например, [Бригхем, Гапенски]).
2.9.2. Линейное программирование
Термин "программирование", вошедший в отечественную экономическую литературу в 60-е годы XX
в., имеет несколько значений. Во-первых, этим термином обозначается процесс подготовки специальной
программы для ЭВМ; во-вторых, программирование используется как некоторый синоним терминов
"планирование" и "прогнозирование". В последнем случае обычно говорят об оптимальном
программировании, понимая под этим методы разработки планов и программ, позволяющих
оптимизировать некоторые стороны деятельности хозяйствующего субъекта. Особенность методов
оптимального программирования заключается в активном использовании достаточно сложных
экономико-математических методов. Оптимальное программирование включает несколько разделов,
различающихся разной степенью проработанности и практической приложимости: линейное,
квадратическое, динамическое программирование и др.
Метод линейного программирования, наиболее распространенный в прикладных экономических
исследованиях ввиду его достаточно наглядной интерпретации, позволяет хозяйствующему субъекту
дать обоснование наилучшему (по формальным признакам) решению в условиях более или менее
жестких ограничений, касающихся доступных для предприятия ресурсов. С помощью линейного
программирования в анализе финансово-хозяйственной деятельности решается целый ряд задач, в
первую очередь относящихся к процессу планирования деятельности, который он позволяет отыскивать
оптимальные параметры выпуска и способы наилучшего использования имеющихся ресурсов.
Суть метода линейного программирования заключается в поиске максимума или минимума
выбранной в соответствии с интересами аналитика целевой функции при имеющихся ограничениях.
Рассмотрим использование этого метода на примере 2.15.
Пример 2.15. Фабрика по производству чая выпускает две марки этого продукта. Условное наименование
марок - А и В. Отпускная цена чая марки А - 60 руб. за килограмм, марки В - 50 руб. за килограмм. Каковы
должны быть оптимальные годовые объемы производства чая обеих марок, чтобы выручка фабрики от их
реализации была максимальной?
Пусть оптимальный объем производства чая марки А составит X тонн в год, а марки В - у тонн в год.
Суммарная выручка от их реализации составит (60x + 50y) тыс. руб. Решение задачи подразумевает поиск такой
комбинации (х, у), которая позволила бы обеспечить максимум этой функции, т.е. поиск
Понятно, что чем больше будет выпуск и той, и другой марки, тем больше будет выручка, однако ресурсы
фабрики небезграничны. Для изготовления обоих сортов чая используется одно и то же оборудование, общая
производительность которого составляет 300 тонн продукции в год. Таким образом, ограничение по мощности
оборудования выглядит следующим образом:
При изготовлении чайных смесей разных марок используют чайный лист двух сортов: в состав чая марки А
входит 70% 1-го сорта и 30% 2-го сорта, в состав марки В - 20% 1-го сорта и 80% 2-го сорта. Стоимость сырья 1-
го сорта составляет 38 руб. за килограмм, 2-го сорта - 24 руб./кг. Таким образом, себестоимость чайного листа,
необходимого для производства одного килограмма чая марки А, составляет 33,8 руб. (0,7 ∙ 38 + 0,3 ∙ 24 = 33,8), а
марки В - 26,8 руб. (0,2 ∙ 38 + 0,8 ∙ 24 = 26,8).
Фабрика может тратить на закупку сырья не более 9000 тыс. руб. в год. Следовательно, на объем выпуска
69
накладывается еще одно ограничение финансового порядка:
Понятно, что искомые величины объемов производства разных сортов чая (x и у) должны быть положительны.
Таким образом, полная формулировка задачи линейного программирования в данном случае будет следующей:
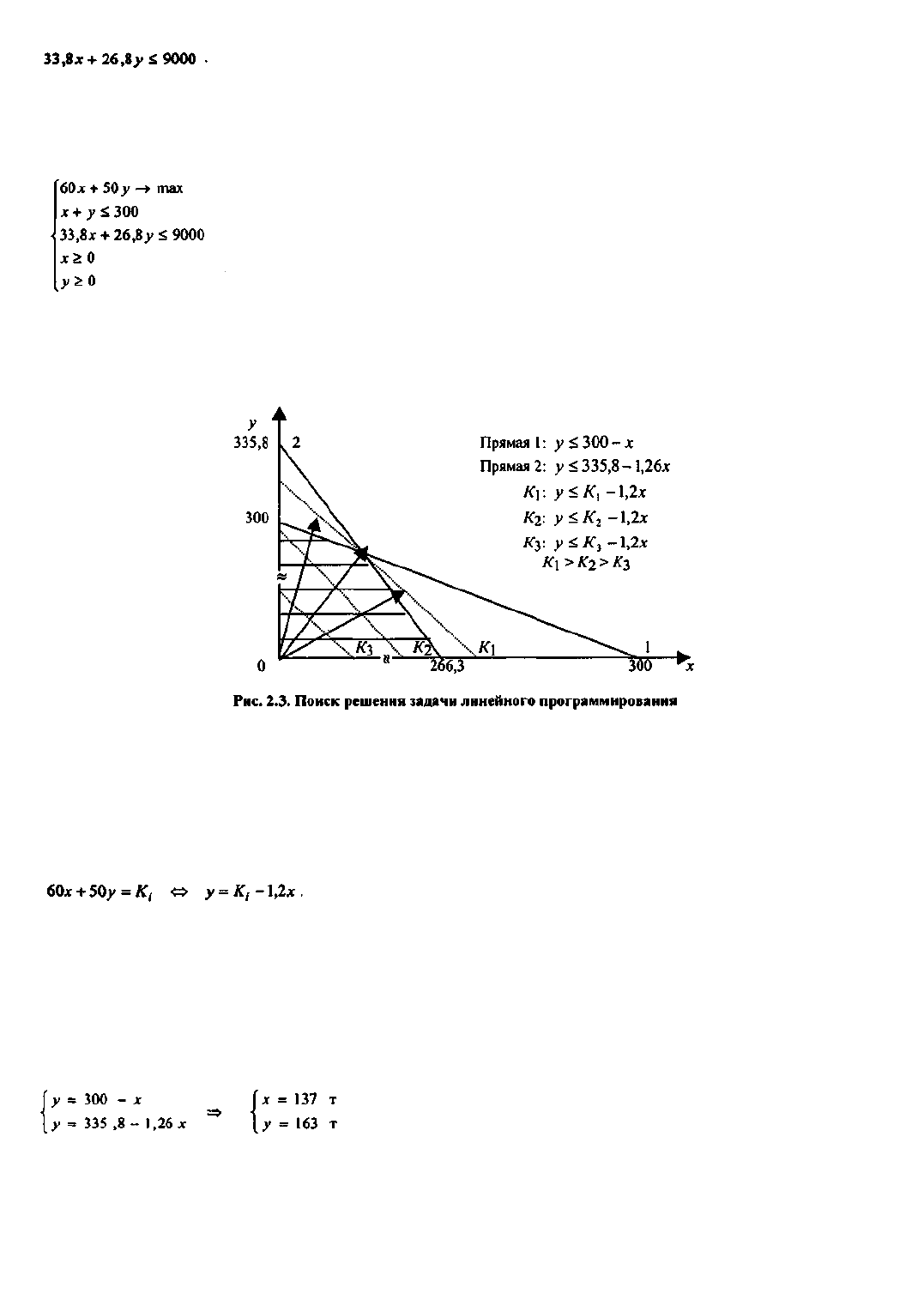
Для решения этой задачи найдем область возможных значений х и у графическим способом (рис. 2.3). Для
этого сначала найдем на плоскости (х, у) область, соответствующую всем четырем ограничениям.
На рис. 2.3 прямая 1 соответствует производственному ограничению, прямая 2 - финансовому; двум
оставшимся ограничениям соответствуют сами оси х и у. Таким образом, удовлетворяющие всем ограничениям
значения (х, у) лежат в заштрихованной области. Какая же точка этого пятиугольника будет искомым решением?
Нам требуется найти такое значение К, которое позволило бы максимизировать целевую функцию на
заштрихованной области. Для этого рассмотрим множество функций вида
Три из этих функций приведены на рис. 2.3 пунктирными прямыми. Чем дальше по направлению стрелок от
центра координат находится прямая, тем большему значению К
i
она соответствует. Очевидно, что на
заштрихованной области функция (60x + 50у) примет максимальное значение в точке пересечения прямых 1 и 2.
Следовательно, координаты этой точки будут искомым оптимальным решением, максимизирующим целевую
функцию.
Найденное алгебраическим методом решение этой системы уравнений будет таким:
Именно такое соотношение объемов выпуска чая сортов А и В позволит фабрике при существующих
технологических и финансовых ограничениях получить максимальный объем выручки.
Существует множество компьютерных программ, позволяющих отыскивать решения в задачах с
десятками и даже сотнями параметров и ограничений. Рассмотренный нами в примере 2.15 случай
представлял собой задачу оптимизации выпуска при двухпродуктовом производстве (марки А и В).
70
