Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Cyclic Plasticity with an Application to Extremly Low Cycle Fatigue 439

Denoting the output value at

ε = β by f

α,β

from the limiting triangle, it follows that

()

2,ff P dd

αα

αβ α

′

ββ

⎛⎞

′′ ′ ′

−=− α

⎜⎟

⎝⎠

∫∫

(3)

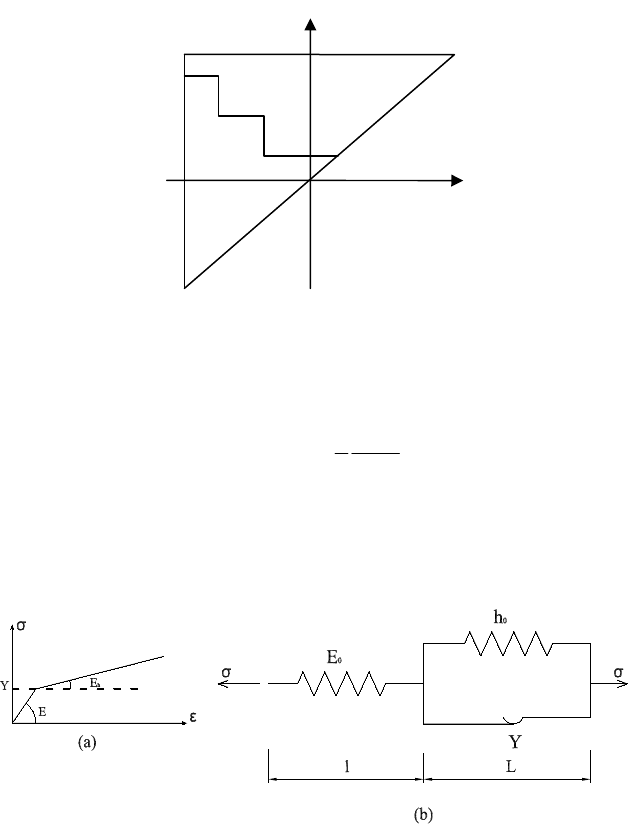
Fig. 2. Limiting triangle with the interface staircase line L(t)

By differentiating expression (3) twice, with respect to α and β, the Preisach

weight function is derived in the form

()

∂

αβ =

∂α∂

(4)

The Preisach model explained above possesses two properties: wiping out and

congruency properties. Those properties and much more about Preisach model is

explained in the (Lubarda et al., [2]) and (Lubarda et al., [3]).

Fig. 3. (a)Elastic-linearly hardening stress-strain behaviour with elastic modulus E, initial

yield stress Y and hardening modulus E

(b) Three-element unit reproducing the stress-

strain behaviour in (a)

, -α

, α

L(t)

(t)

440 D. Šumarac and Z. Petrašković

-Y

(-σ0,-ε0)

(σ0,ε0)

fα,β

fα

3 The Preisach Model for Cyclic Behaviour of Ductile

Materials

One dimensional hysteretic behavior of elasto-plastic material can be successfully

described by the Preisach model. Ductile material is represented in various ways

by a series or parallel connections of elastic (spring) and plastic (slip) elements

(Lubarda, at al., [2]). These results have advantage in comparison with classically

obtained (Iwan, [4]) because of simplicity and strict mathematical rigorous proce-

dure. Parallel Connection of elastic and slip elements, Series connection of elastic

and slip elements are discussed elsewhere (Sumarac and Stosic, [5]), (Lubarda, at

al., [2]). Here we will consider a three element unit.

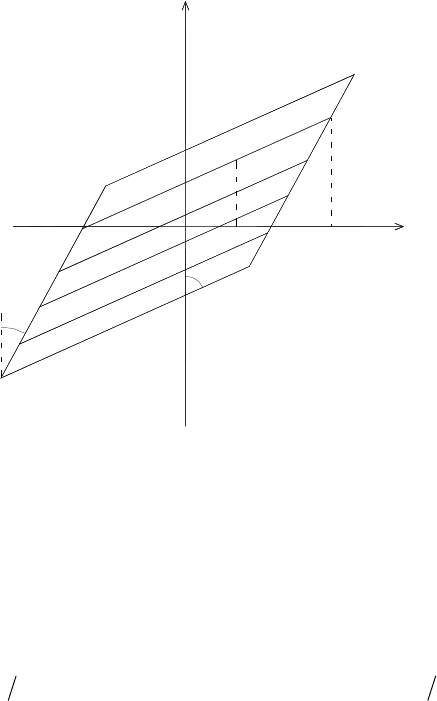
Fig. 4. Major hysteresis loop and several transition lines, corresponding to the material

model in Fig. 3

3.1 A Three-Element Unit

Elastic-linearly hardening material behavior, characterized by the stress-strain

curve shown in Fig. 3a. (E and E

are elastic and hardening moduli), can be mod-

eled by a three-element unit shown in Fig. 3b. Elastic element of length l and

modules E

is connected in a series with a parallel connection of elastic and slip

element, of length L modulus h

and yield strength Y. It then follows that

()

lLlEE +=

and

()

hEEhE

+= , where

()

LLlhh +=

.The Prei-

sach function can be determined from the hysteresis nonlinearity shown in Fig. 4,

Cyclic Plasticity with an Application to Extremly Low Cycle Fatigue 441

α−β=0

α−β

Ymin

α−β

max

which relates the stress input to strain output. The Preisach function in this case

has support along the lines

0=−

and Y2=−

, i.e. it is given by

() () ()

.Y2

⎥

⎦

⎤

⎢

⎣

⎡

−β−αδ

−

+β−αδ=βα (5)

The expression for strain as a function of applied stress is, consequently,

() () ()

Y2,

⎥

⎦

⎤

⎢

⎣

⎡

σ−

ασ

−αα

−

+ασ

αα

=ε

∫∫

(6)

The first and second term on the right-hand side of (6) are elastic and plastic

strain, respectively. For a system consisting of infinitely many of three-element

units, connected in a series and with uniform yield strength distribution within the

range

maxmin

YYY ≤≤ , the total strain is

() ()

dd)t(

min

max

⎥

⎦

⎤

⎢

⎣

⎡

σ−

βασ

βα

−

+ασ

αα

=ε

∫∫∫

(7)

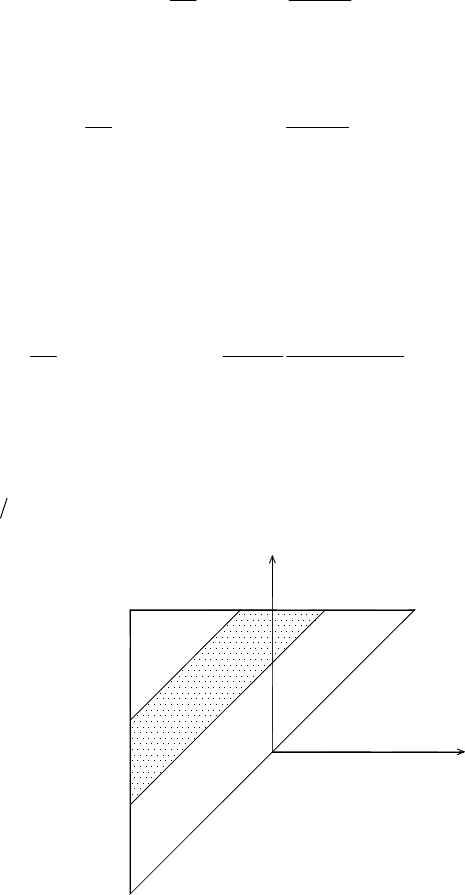
In (7) the integration domain A is the area of the band contained between the lines

min

Y2=β−α and

max

Y2=β−α in the limiting triangle, shown in Fig. 5. The

first term on the right-hand side of (7) is the elastic strain, which can be written as

()

.Etσ

Fig. 5. The Preisach function corresponding to series connection of infinitely many three

element units

442 D. Šumarac and Z. Petrašković

1.0

2.0

3.0

σ/Y

min

-2.0

2.0

0.0

-3.0

3.0 4.0 5.01.0

-1.0

3.5

-4.0

3.5

2.5

1.5

-2.5

-3.5

In the case when the strain is the input and stress output, the Preisach function

becomes

() ()()

⎟

⎠

⎞

⎜

⎝

⎛

−β−αδ−−β−αδ=βα (8)

The stress expression is form (1)

() ()

∫∫

ε−

αε

−αα

−

ε−

−αε

αα

=σ

d)t(

)t( . (9)

3.2 Ilustrative Example

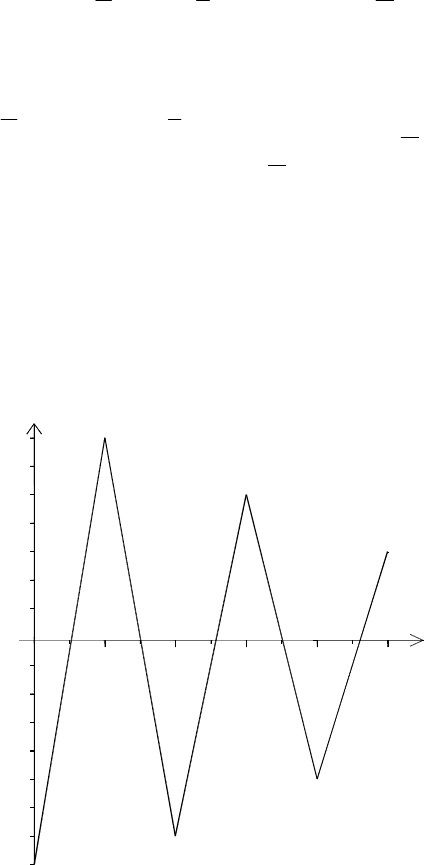
To illustrate the application of the Preisach model the stress-strain hysteretic curve

is determined for material model of series connection of three unite element intro-

duced in the previous subsection. In the calculation it is used

= E/9 and Y

max

min

. The loading history of stress change is shown in Fig.6. From the procedure

explained above the strain in the first portion

-4Y

min

‹ σ ‹ -2Y

min

is linear:

Fig. 6. History of stress input

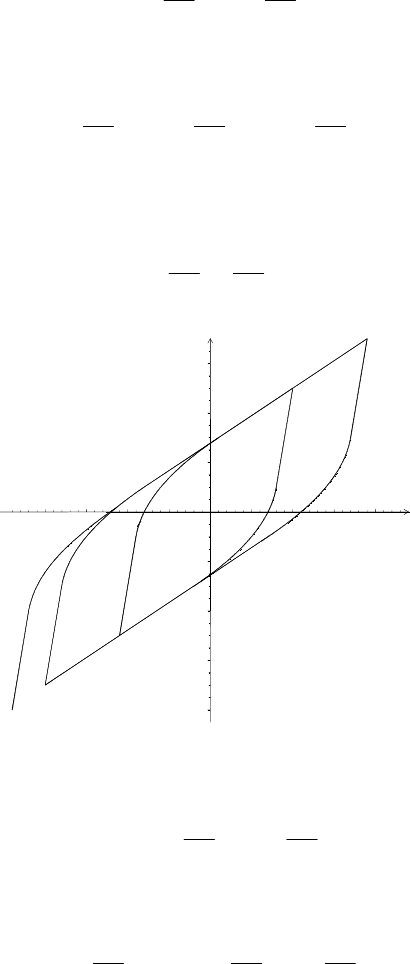
Cyclic Plasticity with an Application to Extremly Low Cycle Fatigue 443

1.0

2.0

3.0

-20.0-24.0

-3.0

-2.0

-1.0

-4.0

εE/Ymin

σ/Ymin

-15.0 -10.0 -5.0 20.015.010.05.0

min min

εσ

=− + (10)

For further increase of stresses in the region

-2Y

min

‹ σ ‹ 0, staircase line L falls in-

to the band are A shown in Fig.5 and consequently response is nonlinear:

min min min

22 2 5 2

YY Y

⎛⎞⎛ ⎞

εσσ

=−+++

⎜⎟⎜ ⎟

⎝⎠⎝ ⎠

(11)

At the stress level

σ=0 the strongest element Y

max

starts to yield. Saturation occurs

and the system responds elastically with the Young’s modulus

=E/9, i.e. in the

region

‹ σ ‹ 3.5Y

min

min min

9 12.5

εσ

=− (12)

Fig. 7. Stress-strain loop

In the region 1.5 Y

min

‹ σ ‹ 3.5 Y

min

response is linear with the Young’s modulus E:

min min

15.5

εσ

=+ (13)

Further decrease of stresses,

-0.5Y

min

‹ σ ‹ 1.5Y

min

, leads to nonlinear response

with the quadratic parabola:

min min min

17 1.5 4 2

YYY

⎛⎞⎛⎞

εσσ

=− − −

⎜⎟⎜⎟

⎝⎠⎝⎠

(14)

In the region,

-3.5Y

min

‹ σ ‹ -0.5Y

min

, saturation again occurs and the system re-

sponds as elastic with the Young’s modulus of

444 D. Šumarac and Z. Petrašković

min min

11.5 9

εσ

=+ (15)

The further procedure is obvious, and the stress-strain loop is presented in Fig 7.

4 Extremly Low Cycle Fatigue

In the literature the Manson-Coffin law is widely used to explain cyclic fatigue of

materials:

()

=Δ (16)

Where

is number of cycles to failure, Δε

is plastic strain amplitude and C and

γ are material constants [8], [9] and [10]. This diagram in Log-Log graph is repre-

sented by linear lines. However experimentally it is shown that eq. (16) overesti-

mates number of cycles in the case of very low cycle fatigue. An atempt to model

extremly low cycle fatigue is given in [7]. Application of Preisach model to solve

this problem will be disscused elsewere. Here, experimental verification of low

cycle fatigue on example of Dampers DC 90 will be shortly explained.

5 Application and Testing of DC90 Dampers

Earthquakes are very dangerous impacts on civil engineering structures. Specially

this is the case of masonry structures. It is well known that those structures have

large mass, and consequently, because of bad cohesion between bricks (stones)

and mortar they crack and suffer damage when exposed to earthquakes. In Fig. 8.

typical masonry structure in the western part of Serbia, after Kolubara earthquake,

4.8 Richter scale is shown. The cracks and damage, due to alternating loading is

along diagonals. Strong need and desire to find a new effective object protection

from seismic loads and realization of the tougher masonry and even concrete con-

structions resulted a new, DC 90 Construction System and associate devices [11],

presented briefly in this article.

Fig. 8. Damage of two store building

Cyclic Plasticity with an Application to Extremly Low Cycle Fatigue 445

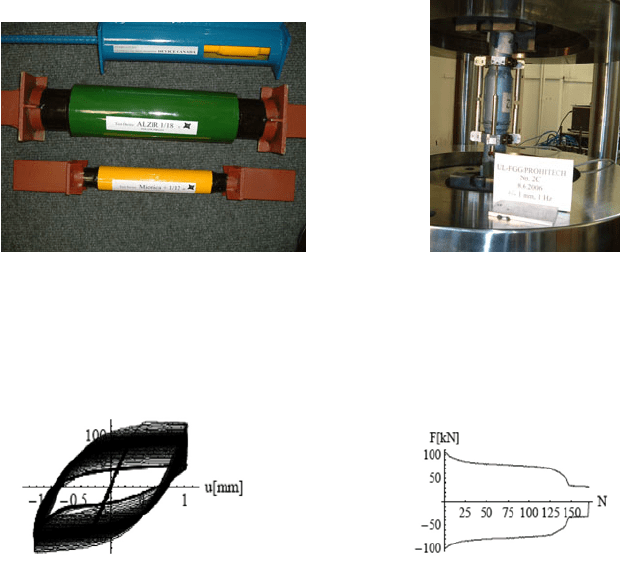
Produced dampers for DC 90 system (Fig. 9) were tested by variable loading on

MTS servo-hydraulic closed-loop machine (Fig. 10) at Faculty of Civil Engineer-

ing and Geodesy in Ljubljana. The test was performed on 18 specimens and ob-

tained hysterezis loop and force-number of cycles to rupture diagram is given in

Fig. 11 for 1mm displacement.

Fig. 9. Typical dampers of DC 90 system Fig. 10. Damper testing

After conducting the serial tests of twelve specimens we demonstrate the tests

for three typical specimens.

Fig. 11. Hysteresis loop diagram and force - number of cycles diagram, for cycle loading at

constant displacement range ± 1 mm.

It is shown that number of cycles before rupture is les than 150 for ±1 mm of

displacement range. With increasing displacement range number of cycles even

decreased, which clearly shows that DC 90 dampers behaves under the earth-

quakes according to very low cycle fatigue.

6 Conclusions

In the present paper it is shown, that Preisach model has several advantages when

it is applied to the problem of so called cyclic stable plasticity of axially loaded

members. Mathematical rigor and a closed form analytical solutions makes the

Preisach model very competitive with the other methods of solution. Application

446 D. Šumarac and Z. Petrašković

of the Preisach model to extremely low cycle fatigue is obvious. Extremely low

cycle fatigue happens in the case of 10 to 20 cycles before rupture, followed by

large plastic strain and maximum stresses much larger than the yield stress. This

case is very important for design of dampers applied for reconstruction of seismi-

cally damaged structures, because Manson-Coffin Law overestimates the number

of cycles before failure.

References

[1] Preisach, F.: Uber die magnetishe Nachwirkung. Z. Phys. 94, 277–302 (1936)

[2] Lubarda, A.V., Sumarac, D., Krajcinovic, D.: Hysteretic response of ductile materials

subjected to cyclic loads. In: Ju, J.W. (ed.) Recent Advances in damage Mechanics

and Plasticity, vol. 123, pp. 145–157. ASME Publication, AMD (1992)

[3] Lubarda, A.V., Sumarac, D., Krajcinovic, D.: Preisach model and hysteretic behav-

iour of ductile materials. Eur. J. Mech., A/Solids 12(4), 145–157 (1993)

[4] Iwan, W.D.: On a class of models for the yielding behaviour of con-tinuous and com-

posite systems. J. Appl. Mech. 34, 612–617 (1967)

[5] Sumarac, D., Stosic, S.: The Preisach model for the cyclic bending of elasto-plastic

beams. Eur. J. Mech., A/Solids 15(1), 155–172 (1996)

[6] Mayergoyz, I.D.: Mathematical Models of Hysteresis, pp. 1–140. Springer, NY

(1991)

[7] Dufailly, J., Lemaitre, J.: Modeling Very Low Cycle Fatigue. Int. J. Damage Mechan-

ics 4, 153–170 (1995)

[8] Manson, S.S.: Behaviour of Materials under Conditions of Thermal Stresses,

N.A.C.A. Tech. Note, 2933 (1954)

[9] Coffin, L.F.: A Study of the Effects of Cyclic Thermal Stresses in a Ductile Metal.

Transactions of the A.S.M.E. 931, 76 (1954)

[10] Šumarac, D., Krajčinović, D.: Elements of Fracture Mechanics. Scientific Book, Bel-

grade (1990) (in Serbian)

[11] Petraskovic, Z.: System of Seismic Strengthening of Structure, Unitet States Patent

and Trademark Office, Pub. No. US 2006/0207196 A1, Serial No. 10/555,131,

September 21 (2006)

The Fracture Toughness of a Highly Filled

Polymer Composite

O.A. Stapountzi

, M.N. Charalambides

, and J.G. Williams

1,2

Mechanical Engineering Department, Imperial College London, UK

School of Aerospace, Mechanical & Mechatronic Engineering,

University of Sydney, Australia

Abstract. Fracture toughness values are given for an ATH-PMMA composite for

filler volume fractions ranging from 0.35 to 0.49 and tested over the temperature

range from 0 to 90 °C. The toughness decreased with increasing filler content con-

trary to expectations. A toughness model based on debonding, and subsequent

plastic void growth was extended from a low volume fraction form to accommo-

date interaction between particles. From the fitted data it was possible to calculate

the adhesion energy of the particles and the average particle size. The former was

somewhat less than the matrix toughness and the latter agreed quite well with the

sizes found from particle size measurements on the filler and surface roughness

measurements on the fracture surfaces.

1 Introduction

Two recent papers have reported results on this ATH (alumina trihydrate) –

PMMA composite containing up to 50% filler content by volume [1, 2]. A high

filler content is used to achieve a high elastic modulus (≈12 GPa) whilst maintain-

ing a sufficient fracture toughness. [1] reported data on fatigue crack resistance

for a single volume fraction over a range of temperatures since this aspect of per-

formance is important practically. In [2] the study was extended to a set of mate-

rials with a range of volume fractions (0.33 – 0.49) in which Young’s modulus

was measured over a range of temperatures [0 - 90°C]. This presented an interest-

ing opportunity to compare the predictions of a range of modulus models since the

temperature variations resulted in the matrix properties changing while the filler

properties remained constant. It was demonstrated that such stiffness properties

could be accurately predicted by several models [2].

This work reports fracture toughness data on a similar set of materials tested

over the same temperature range. This data presents an opportunity to explore

448 O.A. Stapountzi, M.N. Charalambides, and J.G. Williams

toughness models of composites since, again, the matrix properties change with

temperature whilst the filler properties do not. The fatigue data [1] showed a peak

in fatigue crack growth rate (da/dN) at around

50Ԩ

which was attributed to ther-

mal stresses around the particles.

Some recent work on modelling the toughening mechanism in particle filled

composites as plastic void growth resulting from the debonding of the particles [3]

will also be explored here. It has been necessary to extend the earlier, low volume

fraction analyses, to account for the high values used here.

2 Materials and Experiments

Nine materials were used with volume fractions ranging from 0.35 to 0.49. These

were supplied by Du Pont as 12.5 mm thick sheets and prepared by casting the

filled monomer syrup in moulds. The curing process is exothermic so that the

moulds are cooled leading to thermal stresses both in the bulk and on an inter par-

ticle range. The lowest volume fraction was the practical limit for the process and

the upper is close to the theoretical maximum of 0.52 (see section 4).

The fracture toughness tests were performed in accordance to ISO 13586, the

linear elastic fracture mechanics standard for polymers and using three point bend

tests. A specimen thickness of around 5 mm was used and this gave valid results

over the whole temperature range. Notching such materials was a challenge. Ra-

zor tapping was employed but the particles often gave damage around the crack

tip which led to considerable scatter in some of the data. At each temperature a

minimum of five specimens was tested.

The matrix material is a lightly cross linked PMMA but, as in previous papers,

we have assumed that it behaves in a similar manner to normal PMMA. Fracture

tests were performed in the range 20-90

C and compression tests using cylindrical

samples tests were employed to determine the yield stress. The loading times of

all the tests was kept approximately constant. Talysurf measurements were made

on fracture surfaces of samples taken from all the test temperatures to determine

the average roughness values.

3 Experimental Results

Table 1 gives the fracture data for all the composite tests; the data are also plotted

in Fig. 1. The standard deviations are generally less than 10% which is low for

this type of test. The G

values increase somewhat with temperature but the most

notable feature is the decrease with volume fraction. In most cases this decrease is

about 30% over the volume fraction range. This is contrary to expectations and an

increase would be predicted [3].