Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

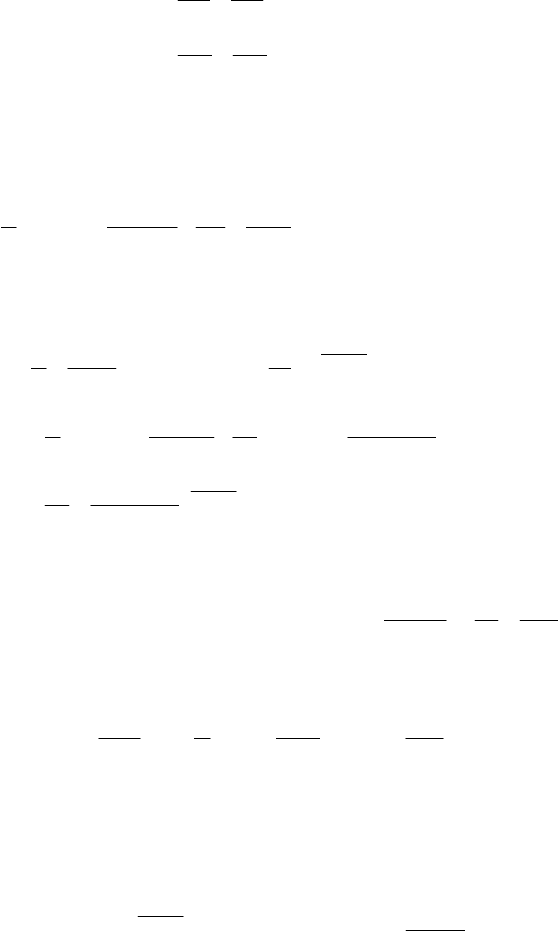
Reinforcement of a Cracked Infinite Elastic Plate with Defects 409

du du

dx dx

bxb

dx dx

υυ

+−

==−<<

(46)

using the expressions (26)-(27) and the known method [1,13] we will have the

following singular integral and integro-differential equations that describe the

problem (state equations):

(), | |

2()

1'()

,||

(), | |1

ρρ

ξξρ

τη

χη η

ησ ρξ

πηξπηξ

σλχξ ξ

−

−−

−− <

⎧

⎛⎞

⎪

+− =−<<

⎜⎟

⎨

⎜⎟

−−

⎪

⎝⎠

−+ <<

⎩

∫∫ ∫

(47)

(1) (1) 0

χχ

−= = (48)

00 0 0

00 0

()

2() ()()

() 1 () ()

'( )

() ()

() () (), | |

div d

ρξ

ρρ

χη

ηχξ χηχηη

πηξ

λχηη ηξ

ηη

πηξ ηξπ

ηξ

χη χη η ξ ξ ρ

ηξπ

−−

−

−−

−

⎡⎤

+=− −+

⎣⎦

−

⎛⎞

−

++ − + −

⎜⎟

−−

⎝⎠

−

⎡⎤

−−+<

⎣⎦

−

∫∫

∫∫ ∫∫

∫



(49)

Definitions of the quantities, dimensionless or not, that were used in the above:

00 0

0000

() () (), () ln

pi f iq

σσ

χξ ξ τξ ξ

−

⎛⎞

=− =−+ +

⎜⎟

⎝⎠

()

() 4( )/ , () 4 / , /, /pp rcaba

ξαξτξταξ ρ

=Ε=Ε==

,, ,()ln,||1

ppq

χξξρ

δδξ

Ε+

=== = <<

ΕΕ−



Here, we have to note that function

()

()| |px x b< expresses the unknown

distribution of the perpendicular stresses on the contact boundary of the stringer

and the plate. The equilibrium equation of the stringer will take the following

form:

00 00

() () 2 ,

diqq

χη χη η

+−

−

⎛⎞

−

⎡⎤

−= =

⎜⎟

⎣⎦

⎝⎠

∫

(50)

the maximum opening of the edges of the springs is given by:

()( )

max

,/rrca

δχ

=± =

410 S.M. Mkhitaryan and D.I. Bardzokas

therefore the density of the normal displacements dislocation on the crack lips and

the dimensionless contact stresses

()p

and

()

are defined by the system of

equations (47) and (49) as well as relations (48) and (50) where

()

()2, /

χρ

δδδα

±= = . After solving that system, the dimensionless normal

stresses outside the crack and on Ox-axis are given by:

()

2()

1'()

,||1

ρρ

τη

χη

σξ η η ξ

πηξπηξ

−−

⎛⎞

=− + + >

⎜⎟

−−

⎝⎠

∫∫ ∫

As examples one can study some special cases of the examined here problem.

First, the case when a total rigid inclusion partially covers the plate

()

baΕ=∞ < , or secondly a totally rigid inclusion that covers the plate

()

baΕ=∞ =

. In the last case we will get the known result of [14] (for 0

= ).

7 Conclusions

In this work a series of problems of the linear elasticity for cracked bodies with

reinforcements, that are classified as contact problems, are treated with the help of

Complex Analysis and the Theory of Singular Integral Equations. With this work

we can chose the optimal position of the reinforcement, so that we can achieve

lower stress intensity factors (SIF) in the edges of the crack; but also to calculate

the distribution of stresses outside and on the crack lips.

References

1. Alexandrov, V.M., Mkhitaryan, S.M.: Contact problems for bodies with thin covers

and layers. Moscow, Nauka (1983) (in Russian)

Gevorgyan, S.K., Manukyan, E.H., Mkhitaryan, S.M., Mkrtchyan, M.S.: The mixed

problem for anisotropic compound wedge with a crack. In: Modern problems of

deformable bodies. Mechanics, Collection of papers, Yerevan, Armenia. Dedicated to

the memory of Prof. P.S. Theocaris, vol. 1, pp. 98–113 (2005)

Bardzokas, D., Parton, V.Z., Theocaris, P.S.: Integral equations of elasticity for a

multiconnected domain with inclusion. Journal of Appl. Math. and Mech.

(P.M.M.) 53(3), 375–384 (1989)

Bardzokas, D.I., Filshtinsky, M.L., Filshtinsky, L.A.: Mathematical methods in

electromagnetoelasticity. Springer, Heidelberg (2007)

Rose, L.R.F.: Crack reinforcement by distributed springs. J. Mech. Phys. Solids 35(4),

383–405 (1987)

Melan, E.: Ein beitrag zur theorie geschweisster verbindungen. Ingr-Arch 3(2), 123–

129 (1932)

Thecoaris, P.S.: Numerical solution of singular integral equations: Methods. J. Eng.

Mech. Div. ASCE 107, 733–752 (1981)

Theocaris, P.S.: Numerical solution of singular integral equations: Applications.

J.Eng.Mech. Div. ASCE 107, 753–771 (1981)

Reinforcement of a Cracked Infinite Elastic Plate with Defects 411

9. Bardzokas, D.I., Gevorgyan, J.K., Mkhitaryan, S.M.: About a stress deformation

condition of piecewise-uniform wedge with a system of collinear cracks at an antiplane

deformation. Mathematical Problems in Engineering 2, 245–268 (2005)

10.

Bardzokas, D.I., Mkhitaryan, S.M.: About an interaction of stress concentrators of

various types. In: Proceedings if Int. Conf. dedicated to the 95th Anniversary of

Academician N.K. Arutyunyan, Yerevan, pp. 91–96 (2007)

11.

Savruk, M.P.: Stress intensity factors in cracked bodies. Mechanics, fraction and

endurance of materials. In: Panasynk, A.V.V. (ed.), vol. 2 (1998) (in Russian)

12.

Shtaernan, I.Y.: Contact problems of theory of elasticity. Moscow – Leningrad,

Gostehigdat (1949) (in Russian)

13.

Buffler, M.: Sceibe mit endlisher elastischer versteilung. VDI-Fossehung Sheft 485,

Ausgabe B., Bd 27, S 44 (1961)

14.

Cherepanov, G.P.: “Mechanics of brittle fracture”. Moscow-Nauka (1974) (in Russian)

Some Actual Problems of Fracture Mechanics of

Materials and Structures

Volodymyr Panasyuk and Ihor Dmytrakh

Karpenko Physico-Mechanical Institute of National Academy of Sciences of Ukraine

5 Naukova Street, 79601, Lviv, Ukraine

panasyuk@ipm.lviv.ua, dmtr@ipm.lviv.ua

Abstract. Some theoretical and experimental results on fracture mechanics of ma-

terials and durability of structural elements are presented. Conceptual bases

(statements) of fracture mechanics and strength of cracked materials as well as ur-

gent problems of prospective investigations in this field of science about materials

and their strength are formulated. The actual problems of fracture mechanics and

strength of materials in service environments are considered.

1 Introduction

Development of new machines, structures and means of transport as well as goods

production require design of new materials and data on their physicomechanical

characteristics (strength, plasticity, hardness, resistance to aggressive media effect,

the influence of constant or time variable external loadings, etc). For a long time

have people paid much importance to accumulation of data on such properties. As

a result the science about physicochemical properties of materials, strength in par-

ticular, their integrity, fracture and durability under given service conditions have

been created, methods of these properties prediction have also been developed.

In the first half of the 20

century in the engineering practice there were already

a number of physicomechanical statements (hypotheses, experimental generalisa-

tions, and postulates) for the assessment of the serviceability of the material under

loading. These theoretical and experimental data, and also methods based on these

methods for assessment of materials strength and fracture form the „classical ap-

proaches” of fracture mechanics and structural integrity.

In the frames of classical approaches the methods for assessment of structural

elements strength and durability have been developed; methods for determination

of basic physicomechanical characteristics for macrovolumes of structural elements

have been created too. The size of the specimen of this material is by an order

or two larger than the typical size of the material microstructure. These approaches

are widely used in engineering practice, but in many cases they can be used for

the assessment of structural elements serviceability under the non-extreme service

414 V. Panasyuk and I. Dmytrakh

conditions. But under severe conditions, in particular when structural elements con-

tain sharp stress notches or cracks, classical criteria are insufficient. For such cases

it is necessary to expand the basic statements of the classical mechanics of materi-

als and to formulate new, physically sound schemes-models for such problems so-

lution. As a result of theoretical and experimental researches into this problem in

the middle of the 20

century a new direction in the science on materials strength

and fracture – fracture mechanics and strength of bodies with cracks (or abbrevi-

ated as materials fracture mechanics (MFM)) was created. Materials fracture me-

chanics formulated new approaches – new paradigm – for the strength assessment.

2 Classical and Non-classical Approaches

Let us formulate in short the main postulates of classical and non-classical ap-

proaches. In classical approaches and phenomenological criteria, when evaluating

the strength of materials and structures, a structural element was considered as a

continuum (solid) with given rheological properties (e.g. an elastic continuum).

Fig. 1. Material fracture: classical (a) and non-classical (b) charts; non-classical chart of

fracture at the crack tip (c)

It is assumed [1, 2] that the element of the deformed body is in one of such

states (see Fig. 1a): continuous state (C-state) or fractured state (P-state). Transi-

tion of the element from state C to state P (fracture process) occurs instantane-

ously, if only the stress-state state calculated by the assumed rheological model

attains some critical level (e.g. if tensile stresses at least at one point of a body

reach the material macrovolumes (

σ ) strength under its tension).

Application of the classical approach to the bodies (materials) with cracks does

not allow estimating their strength. For example, if one uses such an approach dur-

ing the assessment of the tensioned plate with an elliptical hole, when the elliptical

hole transforms into a crack-cut, then one would receive a physically non-sound

result – such an approach, according to the postulate formed above states out that

in this case the plate strength equals zero. In reality experimental data show that

strength of such a plate does not equal zero but depends on the crack length and

physical characteristics of the plate material. This is related with the fact that in

the classical approach the special stress-strain state at the tip of a sharp defect-

crack is not taken into account during deformation of a body.

Some Actual Problems of Fracture Mechanics of Materials and Structures 415

The main idea of the non-classical approach (fracture mechanics) is the follow-

ing: it is assumed that during the transition of the deformed body element from C-

state to P-state a certain intermediate П-state is formed (Fig. 1b), which should be

considered when solving the problem on strength of materials with crack-like de-

fects [1, 2].

An important feature of the deformed solid regions, where P-states (regions of

the material prefracture) appear, is the fact that the material here is always de-

formed beyond the stress limit. Just in these regions of the material occur the in-

tensive processes of plastic yield, interaction with the environment, diffusion

processes, material damaging etc. All this causes local fracture of the material, i.e.

C→П→P-transitions.

Thus, non-classical fracture chart (Fig. 1b), put into the basis of the modern

fracture mechanics, takes into account the П-state of the material in deformed sol-

ids (such states arise mainly at the tips of crack-like defects, Fig. 1c).

In the second half of the 20

century fracture mechanics of materials as a mod-

ern science on strength and structural integrity intensively developed in different

countries of the world: in Great Britain, China, Italy, Germany, Poland, Russia,

USA, Ukraine, Hungary, France, Japan and other. Speaking about the scientists

who founded the basis of fracture mechanics and who were the first to implement

the ideas of non-classical approach to the assessment of the deformation of the

solid with sharp stress concentrators we must mention A. Griffith, G. Irwin, K.

Weighard [1–8]). (In [3] one can find publications about the history of fracture

mechanics development).

3 Griffith–Irwin Concept

A. Griffith (1920, 1924) was the first to consider the presence of П-states in the

stress-strained body (material) at the crack tip and to formulate the criterion (con-

dition) of crack growth and formation of new surface (fracture) of a body, using

not a classical approach but a generalized energy balance of a deformed solid with

a crack and the energy that is spent for the formation of new surface during crack

propagation. He was also first who formulated a known energetic criterion of

crack propagation in a deformed body [9]. The establishment of the structure of

stress field asymptotic and displacements at the crack–cut in the deformed solid

(see ref. in [1–3]) was a very important stage in fracture mechanics development.

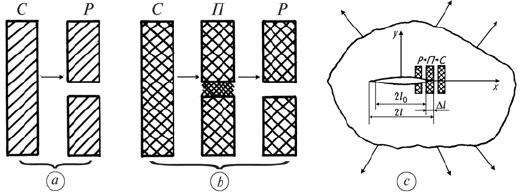
Thus it was shown that the stress tensor components (

σ , Fig. 2) near the crack

tip can be written as:

{}

I0 1 II0 2 III0 3

() () () 0(1),

ij ij ij ij

Kf K f K f

σ = θ+ θ+ θ +

(1)

where

,,,ij xyz=

in Cartesian coordinate system or ,,,ij r z=θ in polar (cylindri-

cal) coordinate system;

() () ()

I0 I0 II0 II0 III0 III0

,, ,, ,K K pl K K pl K K pl== =

are the stress intensity factors (SIF) that are the functions of the body configuration,

416 V. Panasyuk and I. Dmytrakh

crack dimensions

()

l and loading p ;

()

kij

∫ are known functions ( k = 1, 2, 3);

0(1) is a limited value at

0r → .

Fig. 2. Local system of coordinates at the crack front (line 0z) and components (I, II, III) of

the vector of crack edges displacements

Considering dependences (1) in 1957 G. Irwin formulated [10] a new criterion

of limiting-equilibrium state for a cracked body under quasistatic loading for the

case when mode I fracture (Fig. 2) occurs in a body, i.e. when

0K ≠ , аnd

II0

0K = ;

III0

0K = . This criterion is based on the statement that the external

p will be limiting equilibrium

()

∗

= when for a deformed cracked

body the stress intensity factor

()

,Kpl is equal to

K – some constant for the

given material, i.e.

()

I0 I0 I

KKplK

∗

II III

0, 0.KK== (2)

Under the brittle fracture conditions that is when

llΔ≤ (see Fig. 1c), G. Irwin

proved the equivalency of criterion (2) and A. Griffith energy concept.

4 Linear Fracture Mechanics

The Griffith–Irwin calculation models form the basis of the so-called linear fracture

mechanics of solids. The main peculiarity of this part of fracture mechanics is that

the typical dimensions of the region near the crack tip (П-state) where material is

deformed beyond the elastic limit, are considered to be small in comparison with the

crack sizes and the body itself. The stress-strain state in this body is determined by

solving the corresponding problems of linear theory of elasticity for bodies contain-

ing cracks-cuts (that’s why this part is called linear fracture mechanics, LFM). Using

the obtained solutions the SIF values (

()

Kpl, i = І, ІІ, ІІІ) are calculated, and

Some Actual Problems of Fracture Mechanics of Materials and Structures 417

criteria (2) is used. Crack growth resistance values (

IIIIII

cc c

KK K) are deter-

mined experimentally [14–15].

In the cases when the cracked solid is under the complex loading, i.e. when all

SIFs do not equal zero (

IIIIII

0, 0, 0KK K

θθ θ

≠≠≠) for the estimation of limiting

loading value (

∗

= ) the following criteria equation (as a phenomenological

generalization of Griffith–Irwin criteria) is used:

12 3

I II III

nn n

cc c

KK K

∗∗ ∗

θθ θ

⎛⎞⎛ ⎞⎛ ⎞

++ =

⎜⎟⎜ ⎟⎜ ⎟

⎝⎠⎝ ⎠⎝ ⎠

, (3)

where

123

,,nnn,

K ,

IIc

K ,

IIIc

K are characteristics obtained experimentally

(see references in [14–16]).

Relatively criteria equation (3) it is necessary to mention that for all possible

SIFs it requires yet experimental approbation and theoretical development, in par-

ticular the estimation of such a criteria not by phenomenological generalization

but by formulation of the certain calculation model, and construction on this base

of certain criteria, in particular when some SIFs are negative. Some experimental

results on this problem are published in [16–18]. These and other problems of

LFM are important nowadays too.

For practical realization of LFM according to criteria (1)–(3) it is necessary to

know the value of the material crack growth resistance, that is the characteris-

tics

K ,

IIc

K ,

IIIc

K , and parameters

123

,,nnn. Today [19, 20] methods for ex-

perimental determination of the materials resistance to crack growth (

K ) have

already been developed and standardized. Concerning the establishment of the

material crack growth resistance characteristics under mode II (Fig. 2) displace-

ment of crack faces (displacement perpendicular to the line of the crack front)

IIc

K , i.e. when

0K = ,

0K ≠ ,

III

0K = , and also under the mode III (Fig. 2)

displacement of the crack faces (displacement parallel to the line of the crack

front)

IIIc

K , i.e. when

0K = ,

III

0K ≠ , we have no yet unified meth-

ods (standards) for the experimental determination of mentioned characteristics

and there is no the appropriate data base of these characteristics for different struc-

tural materials. Preparation of reference books on these characteristics is a very

important task for engineers and scientists.

Factors

123

,,nn n are determined using the experimental results or modelling

of the crack process zone under complex loading. The known investigations [21]

show (in the frames of the generalized

-model of the crack propagation) that

these factors can be considered as being equal

123

4nn n=== or equal

123

2nn n=== on the basis of approximate phenomenological approach.

Thus, we know factors

()

I,II,III

Ki= and parameters

()

1, 2, 3

ni= for prac-

tical use of equation (3) of the limiting-equilibrium state of the deformed cracked

body under complex loading. It is necessary for each concrete case to set up

K ,

418 V. Panasyuk and I. Dmytrakh

IIc

K and

IIIc

K values. The value of

K is found in the reference book or is de-

termined according to known standard [19, 20].

Test methods for the determination of factors

IIc

K and

IIIc

K are developed

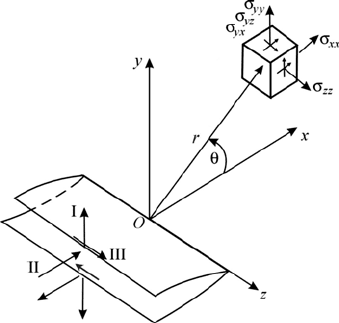
[23, 24] for a tubular specimen with a circular crack (Fig. 3).

Fig. 3. Specimen for crack growth resistance of material (K

IIc

, K

IIIc

) determination: 1, 2 –

circular concentrator; 3, 4 – symmetrical cracks; 5, 6 – places of specimen gripping during

torsion (K

IIIc

) or tension (K

IIc

)

Experimental verification of criteria equation (3) was done in works [23, 24] under

investigation of the limiting-equilibrium state of materials under the complex loading

of cracked specimens. The fracture of these specimen occurred under the mixed-

mode fracture macro-mechanisms, that is: mode I–mode II, and mode I–mode III.

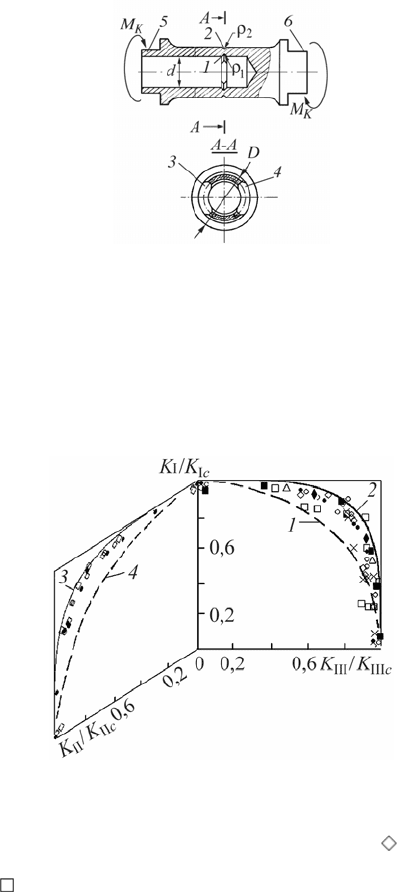
Fig. 4. Diagram of limiting-equilibrium state of а deformed cracked solid under complex

loading and realization of fracture macro-mechanism (І + ІІ) (а) and (І + ІІІ) (b) (curve 1 –

according to formula (3) when n

= 4, and curve 2 – according to formula (3) when n

= 2):

○ – 40ХН steel, quenching in oil at 1123 K, tempering at 833 K;

– 30ХНГСНА steel,

normalized; – 40Х steel, quenching in oil at 1133 K, tempering at 773 K (results of Ya.

Ivanytskyi); b:

– 4340 steel (results of A.Chyzhyk); aluminium allow 2219 (Е87) (results

of A. Chyzhyk); ¯ – 9ХФ steel: ¡ – quenching in oil at 1133 K, tempering at 873 K; ■ –

tempering at 773 K; U – tempering at 673 K (results of Ya. Ivanytskyi)