Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics
Подождите немного. Документ загружается.


Some Actual Problems of Fracture Mechanics of Materials and Structures 419
It is stated that criteria (3) agrees well with experimental data for deformed-
strengthened materials (
σσ 1, 4
BT
> ), when
i
n = 4, and for deformed-softened
materials (
σσ 1, 4
BT
< ) when
i
n
= 2. All experimental data are situated in the
region bounded by curves 1 and 2 (Fig. 4).
Thus it is possible to plot diagrams of limiting-equilibrium state of structural
elements with available cracks or sharp stress concentrators under complex load-
ing of the structure in the frames of LFM. But we still have no appropriate appro-
bation of criteria (3) for cases when one of SIFs is negative.
5 Non-linear Fracture Mechanics
It is known that prior to failure of real structural materials, first of all metals, the
plastic zones at the stress concentrators, in particular crack-like defects, are
formed. The typical linear dimensions of such zones (П-states) can be commensu-
rable with the defect size or the typical linear size of the deformed body. In such
cases the application of the Griffith-Irwin concept (LFM) without additional re-
finements is not correct.
To solve these problems different deformation criteria, in particular the crite-
rion of critical crack tip opening displacement (CTOD criterion) and also the con-
cept of the
с
δ -model for evaluation of crack opening displacement near its tip,
proposed in [22-24] (1959,1960), are used. The given concept was the beginning
of the investigations in non-linear fracture mechanics of materials, i.e. when the
typical linear dimension of the region of plastically deformed material at the sharp
stress concentrator-crack (П, Fig. 1) is commensurable with the typical size of a
defect or a body (
0
llΔ≈ , Fig. 5).
Fig. 5. A plate with a central crack (2l
0
) and model plastic zones (Δl); δ
р
– displacement of
the initial crack edges in the deformed body under loading p

420 V. Panasyuk and I. Dmytrakh
According to the
с
δ -model the regions of the body (Fig. 5) where plastic zones
have appeared, are modelled by a cut (cuts) opposite sides of which are attracted
with stresses
0
σ , which are the averaged local stresses arising in the plastic zone
of the material (for materials without hardening we can assume that
0 T
σ≈σ,
where
T
σ is yield stress of the material). At all points of the deformed body (out-
side the cuts) the deformations are elastic. Crack opening
p
δ near the initial crack
tip (mutual displacement of edges) at the moment of the crack start is equal to
constant
()
c
δ of the material (Fig. 5). Within the framework of the accepted
model for elasoplastic material there exists the equality
0
σδ 2
c
=
γ
between val-
ues
с
δ ,
0
σ and density of material fracture
γ
, where
γ
is the average value of
the energy necessary for formation of the surface unity in the given material.
Similar approaches, however partial and developed somewhat later, were pro-
posed by D.S. Dugdale [26] (1960) and A.A. Wells [27].
The concept of the
с
δ -model was realized for the first time by M.Ya. Leonov
and V.V. Panasyuk, M.Ya. Leonov and P.V. Vytvytskyi on the example of the
generalized problem of A.A. Griffith and M.Ya. Leonov and V.V. Panasyuk using
the Sack's generalized problem (see ref. in [25]).
For the generalized Griffith problem i.e. for the cracked plate under tension
(Fig. 5) when the value of plastic zone
()
lΔ is commensurable with
0
l (
0
llΔ≈ )
in the frames of the
с
δ -model the value of the limiting loading pp
∗
= and
p
δ value was established for the first time (1960) as
00
0
00
8
2
σ arccosexp , ln cos ,
π 2
p
l
d
p
p
lE
∗
∗
⎛⎞ ⎛ ⎞
σ
π
⎛⎞
=−δ=−
⎜⎟ ⎜ ⎟
⎜⎟
πσ
⎝⎠
⎝⎠ ⎝ ⎠
(4)
where
()()
0
8
c
dE
∗
=πδ σ ; E is Young’s modular,
с
δ is material constant.
The size of the area of inelastic (plastic) deformations in the crack plane (the
value of the zone П) in this case is determined by the equality
00
0
sec 1
2
p
p
dlll
⎡
⎤
π
=− = −
⎢
⎥
σ
⎣
⎦
. (5)
Formula (4) can be used for the crack of any initial length
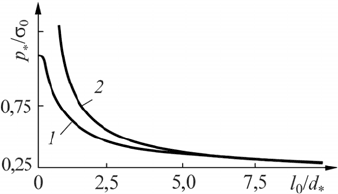
00
0lldf
. Accord-
ing to this formula the critical loading
p
∗
is always finite and (when
0
0l → )
tends to
0
σ . This physically sound result is not obtained in the Griffith–Irwin the-
ory (Fig. 6).
Some Actual Problems of Fracture Mechanics of Materials and Structures 421
Fig. 6. Specimen for crack growth resistance of material (K
IIc
, K
IIIc
) determination: 1, 2 –
circular concentrator; 3, 4 – symmetrical cracks; 5, 6 – places of specimen gripping during
torsion (K
IIIc
) or tension (K
IIc
)
In the 80s of the last century (see references in [5]) the
с
δ -model concept was
generalized for mode II and mode III cracks, and the methods of experimental de-
termination of critical opening displacement (
Іc
δ ) and critical displacement (
ІIc
δ ,
ІIIc
δ ) of the crack edges were proposed.
At the beginning of the 90ies M.P. Savruk et al. [28] used the
с
δ -model for
plastic bands, initiating from the crack tip at arbitrary angle.
It should be noted that the effective and reliable experimental methods for the
estimation of deformation characteristics of crack growth resistance (
Іc
δ ) have
not been developed yet. Here we meet difficulties presented in [29]. The precise
analysis of elastic-plastic deformation of the material near the crack tip in the ten-
sioned plate basing on the approach that is grounded on the correlation of speckle-
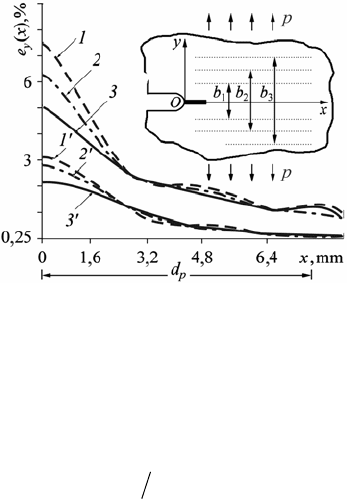
images of the surface in the prefracture zone (Fig. 7) has been done in the above
paper. Here the value of deformation in this zone was assessed at the different
measurement bases
123
(, , )bb b b . Specimens of Д16AT alloy were tested. As a re-
sult the distribution of deformations in the process zone in the loaded and
unloaded plates was established. This distribution is presented in Fig. 7 (curves 1–
3 for different measurement bases
123
(, , )bb b b and
constp =
, and curves 1'–3'
after unloading of the plate accordingly). The received results show that the ex-
perimental determination of critical crack opening displacement (
I
δ
c
) between the
crack edges near its tip is not constant, i.e. these displacements are different de-
pending on measurement base (
b ). At the same time experimental results in Fig. 9
illustrate that the size of the process zone
p
d dose not depend on the measure-
ment base. It remains constant for the given material. This can be used for the
modification of the
δ
c
-model [25], and of the experimental method for
I
δ
c
char-
acteristics determination.
Taking into account the above-mentioned let us consider that the critical length
of the process zone (
d
∗
) to be the material constant. Than using formulas (4)–(5)
422 V. Panasyuk and I. Dmytrakh
Fig. 7. Distribution of deformations e
y
(x) near the crack tip under different measurement
bases b (1 – b
1
= 1.28 mm; 2 – b
2
= 2.56 mm; 3 – b
3
= 3.08 mm) in loaded (1–3) and
unloaded (1′–3′) Д16AT alloy specimen; p = const
for the macrocrack in the plate under tension (Fig. 5) one receives such depend-
ence between the averaged value of the deformational crack growth resistance
(
ȱ
į
с
)
and ( d
∗
) – value of the structural material:
*
10* *
į 8ıʌ,
c
dE d l
0
. (6)
Using formula (6) for experimental determination of
ȱ
į
с
one can avoid difficulties
arising in its direct evaluation, and also those concerning loading amplitudes of
the materials specimen when the incoming macrocrack initiates in it.
The following important task is the experimental approbation of the
ȱ
į
с
charac-
teristics evaluation according to formula (6) and application of this approach to es-
tablishing
ȱI
į
с
,
ȱII
į
с
.
6 Fatigue Crack Nucleation and Growth (Fatigue of Materials)
The problem of materials fatigue is one of the central problems of fracture mechan-
ics and prediction of structural elements lifetime (durability). Great efforts have been
spent by scientists and engineers for this problem solution since the 19
th
century,
when this phenomenon was considered for the first time. The concepts of fracture
mechanics, that is the concepts of cracks initiation and growth in the cyclically
deformed body, are very important for the solution of this problem. If the initiation
period (
i
N ) of the minimum macrocrack in the given material and its propagation
period (
p
N ) are known, the total life time ( N
∗
) is determined by formula:
N
∗
= N
i
+ N
p
,
(7)
where
i
N and
p
N are determined using corresponding theoretical and experi-
mental approaches of fracture mechanics [30], in particular using corresponding
characteristics on materials crack growth resistance.
Some Actual Problems of Fracture Mechanics of Materials and Structures 423
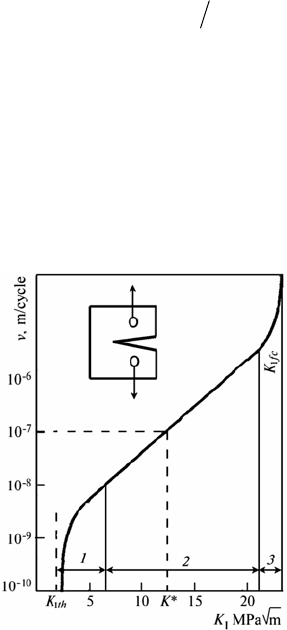
It is known [30, 31] that the material ability to resist crack initiation (resistance
to macrocrack propagation in it) represents the dependence of crack growth rate
(v) on the stress intensity factor (K
I
) or deformation amplitude of the material at
the crack tip (Fig. 8).
As a result of experimental investigations it was shown that such diagrams ((v–
K)-diagrams) are of S-shape and on a certain region 2 (Fig. 8) they can be consi-
dered rectilinear and can be described ([5] volumes 3 and 4) by Paris equation
()
7
II
or 10 ,
m
n
vCK v KK
−∗
== (8)
where K
∗
is the value of K
I
at which the crack growth rate in the given material is
10
–7
m/cycle (Fig. 8); C, K*, m, and n are material constants. To construct the (v–
K)-diagrams the range of the stress intensity factor ΔK
I
(ΔK
I
= K
Imax
– K
Imin
and
ΔK
I
= K
Imax
when K
Imin
= 0) is used instead of the value of K
I
= K
Imax
. Every (v–K)-
diagram is bounded on the left by the threshold value of K
Ith
i.e. by such a value of
K
I
or ΔK
I
that for K
Imax
< K
Ith
(or ΔK
Imax
< ΔK
Ith
) the crack does not propagate. On
the right this diagram is bounded by the value of K
Ifc
i.e. by such a SIF value at
which spontaneous failure occurs (v → ∝).
Fig. 8. Diagram of fatigue crack growth resistance of the material (or (v–K)-diagram): 1 is
the region close to threshold K
th
; 2 is practically rectilinear region; 3 is the region of rapid
crack growth and entire failure under condition K
Imax
= K
Ifc.
So for fatigue fracture of the material we have the following basic fatigue crack
growth resistance characteristics: C, K
Ith
, K
∗
, K
Ifc
, m, n .
For description of complete (v–K)-diagram such formula was proposed in [31]:
0II I I
()/()
q
th fc
vvKK K K
⎡⎤
=− −
⎣⎦
, (9)
where v
0
, K
Ith
, K
fc
, q are material constants, obtained experimentally.
424 V. Panasyuk and I. Dmytrakh
If one takes into consideration that the plastic deformations zone at the fatigue
crack tip is small to compare with the crack length, i.e. in case of macrocrack (Δl
<< l
0
) it is possible to establish [1] the relationship between K
Imax
and
(max)
δ
p
where δ
p
is the distance between the opposite crack edged at its tip under the load-
ing of the body by the force p (Fig. 5).
Using the diagram, of fatigue crack growth resistance (Fig. 8), in particular
formula (9),
p
N value is calculated from the formula:
I
II
,
[()]
() ,
c
l
p
l
cfc
dl
N
vK l
Kl K
∗
=
=
∫
, (10)
where
l
∗
is the minimum length of the macrocrack for this material.
The construction of the minimum macrocrack (
l
∗
) initiation period depending
on the cyclic loading amplitude is a more complicated problem and still has been
no effectively solved. At the same time a certain progress in this direction of in-
vestigations was noticed [30].
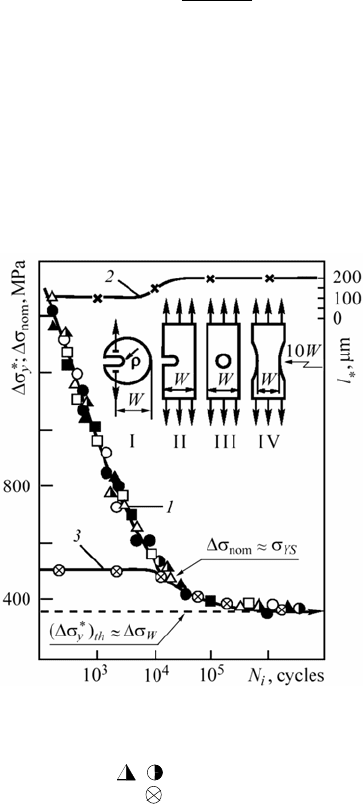
Fig. 9. Dependences of Δσ
nom
∼ N
i
, (curve 1) and l
*
∼ N
i
(curve 2) for notched specimens and
Δσnom ∼ N
i
(curve 3) for smooth specimens of aluminium Д16чАТ alloy; specimen types: І –
W = 64 mm; ρ = 0,75 and 6,5 mm (U,{); ІІ – W = 64 mm; ρ = 0,75 and 6,5 mm (S, z);
W = 30 mm; ρ = 0,75 and 2,0 mm (
, ); III – W = 30 mm; ρ = 0,75 mm (); W = 20
mm; ρ = 0,75 mm (); IV – W = 10 mm (
)

Some Actual Problems of Fracture Mechanics of Materials and Structures 425
Special investigations on the dependence of the period (
i
N ) of the minimum
macrocrack initiation in the plates with concentrators on cyclic loading amplitude
(
*
y
Δσ ) for the Д16чАТ alloy specimens (Fig. 9) were done [30, 32–34]. The
value of the macrocrack was measured by microscope.
On the basis of dependences
()
1yi
fN
∗
Δσ = it is also possible to establish the
threshold value of
у
∗
Δσ for the given material, i.e. the value of (
у
∗
Δσ )
th
below
which
the crack does not initiate. Let us denote this value
у
∗
Δσ (threshold) by
(
у
∗
Δσ )
th
(see Fig. 9). It equals the ordinate asymptote to the curve
()
1yi
fN
∗
Δσ =
when
i
N →∞. The value of (
у
∗
Δσ )
th
is an analogue to fatigue limit (Δσ
R
) of the
material for smooth macrospecimens (without concentrator). That is why (by ana-
logue to Δσ
R
) it can be stated that for amplitude of cyclic loading
у
∗
Δσ <(
у
∗
Δσ )
th
the initiation of the macrocrack near the stress concentrator will not occur and the
fatigue of the material will be not realized.
Ostash O.P. et al [35, 36] established the dependence between the characteris-
tics of macrospecimens fatigue fracture mechanics and characteristics of the mac-
rocrack propagation in the deformed body, and also between the amplitude cyclic
loading (
у
∗
Δσ ) and minimum value of the crack ( l
∗
), that is
І y
Δ 0,886Δ
eff
Kl
∗
∗
=σ,
()
2
І
,
theff R
lK
∗
=η Δ Δσ (η ~ 1,25), (11)
where
І IIeff op
KKKΔ=Δ−Δ,
Iop
KΔ is SIF at which the crack opens; η is the
numerical factor close to unit;
R
Δσ is the fatigue limit of the material on smooth
standard specimens.
Using these correlations, the diagram (
eff
vK≈ ) can be changed by the dia-
gram (
у
∗
Δσ ∼ N
i
) or vice versa. This procedure is shown in Fig. 10. It consists of
such operations.
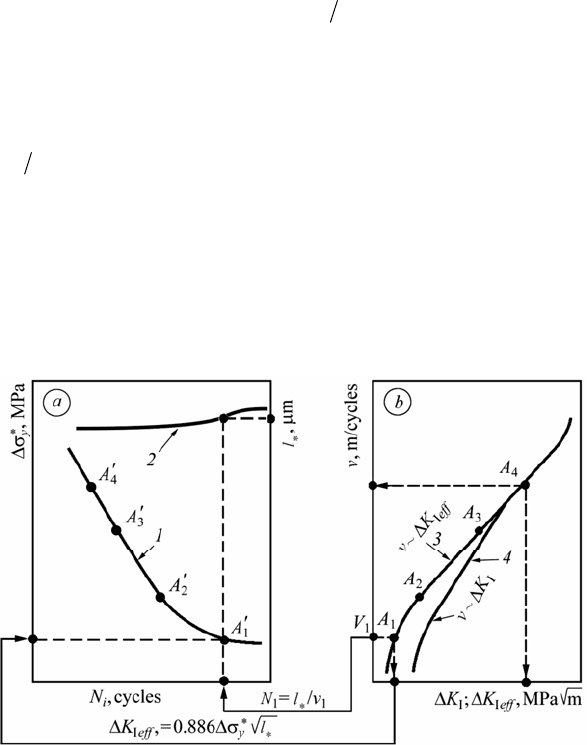
Let us consider a certain point on the (v ∼ K
Іeff
) diagram. For example, this is a
point
1
A on the diagram 3 (Fig. 10b). For this point abscissa
Ieff
KΔ is connected
with values
σ
y
∗
Δ (amplitude of cyclic loading near the stress concentrator or crack
tip) by formula (11). Using this formula one can calculate the value
σ
y
∗
Δ and fix it
as an ordinate of the point
'
1
A on the diagram 1 (Fig. 10а). Further consider the
macrocrack growth to be step-wise (as it is shown in [35]). In means that each time
the macrocrack in the cyclically deformed body grows by a step
l
∗
. So, the average
macrocrack growth rate on diagram 3 (Fig. 10b) is evaluated by formula
426 V. Panasyuk and I. Dmytrakh
ii
vlN
∗
= , (12)
where
i
N is the period of the macrocrack l
∗
formation, this period depends on
the loading amplitude (
σ
y
∗
Δ or
Ieff
KΔ ).
Thus, for the point
1
A on the diagram 3 (Fig. 10b) we have the value
11
Nlv
∗
= . Let us fix this value as abscissa of the point
'
1
A on the diagram 1
(Fig. 10а). Continue this procedure for points
23
,...AA of the diagram 1 (Fig.
10b) and receive corresponding points
''
23
,...AA of the diagram 1 (Fig. 10а). In
such a way we receive the diagram for the determination of the period (
i
N ) of the
minimum macrocrack initiation for the given material near the stress concentrator.
Diagram 2 in Fig. 10а is constructed by formula (11).
Fig. 10. A scheme of construction of the initiation (N
i
) of the minimum length (l
*
) macro-
crack when the amplitude (
σ
y
∗
Δ ) of cyclic loading of the body near the stress concentrator
on the bases of v ∼ K
Іeff
diagram is known
Construction of diagrams 1 and 2 for the evaluation of period (
i
N ) of the l
∗
length crack initiation (Fig. 10a) on the basis of the diagram (v ∼ ∆K
Іeff
) for the
evaluation of the structural elements durability becomes very important for engi-
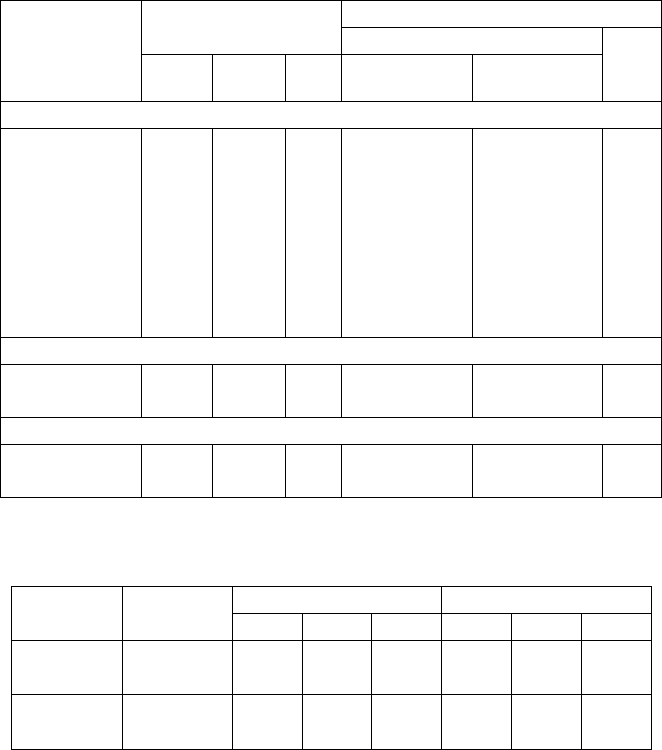
neering practice. Tables 1 and 2 illustrate the application of this approach.
Some Actual Problems of Fracture Mechanics of Materials and Structures 427
Table 1. Experimental and calculated values of the process zone [30, 36, 37]
Value l
*
, μm
Characteristics
Experiment
Material
σ
T
, MPa σ
В
, MPa δ, %
Low-cycle fatigue
(N
i
= 10
3
÷ 10
4
)
High-cycle fatigue
(N
i
= 10
5
÷ 10
6
)
Formula
(11)
Aluminium alloy
Д16T 350 460 15 100 100 135
Д16чAT1 442 475 10 40 180 159
Д16чATН 417 533 17 60 80 100
Д16очT 330 454 22 160 200 237
В95pchT2 456 510 12 100 100 180
В95рчТ3 432 498 14 80 80 78
1420T1 282 431 19 110 110 97
1201T1 340 442 10 130 130 154
Steels
08кп 190 270 48 200 250 208
35ХС2Н3МФ 1700 1950 10 5 10 7
Cast irons
ВЧ50 310 510 14 200 200 158
ВЧ90 850 980 3 50 150 208
Table 2. Experimental and calculation characteristics N
i
, N
p
, N
*
for specimens-bands with a
central hole [36]
Experiment, cycles ⋅10
–3
Calculation, cycles ⋅10
–3
Hole diameter,
mm
Loading range
ΔP, kN
Ni Np N* Ni Np N*
9.0 135 15 150 132.3 10.3 142.6
3.2
12.6 25.2 6 32.2 17.2 4.5 21.7
9.0 118 5 123 100.9 6.6 107.5
5.0
13.5 15.3 3.3 18.6 10.1 2.2 12.3
Thus the proposed concept of the evaluation for structural elements durability
under long-term cyclic loading has a certain experimental confirmation and can be
recommended for engineering practice to determine their life time. Theoretical
and experimental investigations should be continued in order to develop the most
effective and simple procedures for the evaluation of the structural elements dura-
bility in the given service conditions.
7 Interaction between Environments and Deformed Metal
In the mid 50’s of the 20
th
century H.V. Karpenko was the first [37] who discovered
the phenomenon of the steels fatigue limit decrease (approximately by 10–15%) in

428 V. Panasyuk and I. Dmytrakh
surface-active environments (Fig. 11). However, tests on the static tension of steel
cylindrical specimens 10 mm in diameter in the same surface-active environments
showed no influence on the changes of static strength of the steel. This contradiction
was explained by the short-time action of the environment and, as a result, it was
considered that the adsorption effect was not apparent. Such interpretation of the ad-
sorption effect cannot be convincing.
Fig. 11. Fatigue curves under the circular tension of d = 7,62 mm in diameter cylindrical
specimen (40 Х steel, structure – sorbite) under different test conditions: 1 – air; 2 – water;
3 – machine (liquid paraffin) oil, activated by 0.3% of oleic acid [37]
Within the frames of the deformed bodies fracture mechanics concept the fol-
lowing experiment was made [38] taking into account that the fatigue fracture oc-
curs by the crack formation and propagation. A plate with the concentrated forces
P was tensioned as it is shown in Fig. 12.
Fig. 12. Critical loading P = P
*
dependence on the crack length under the tension of glass
plates in dry air (1, 3) and water (3)
