Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Theory and Application of Sampling Moiré Method 229

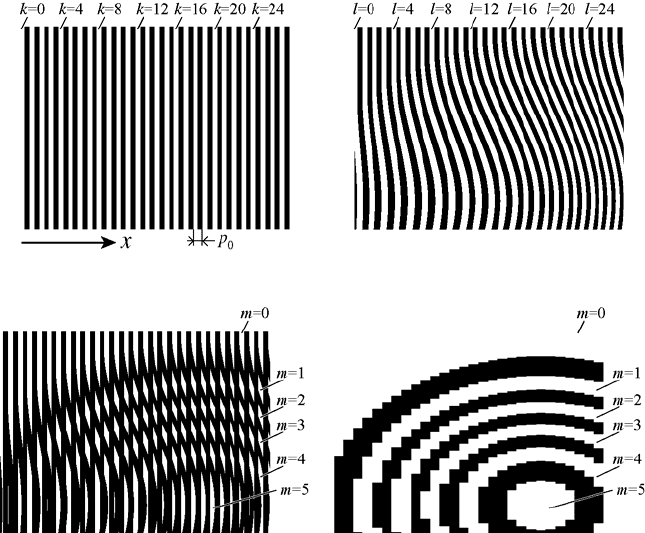
Let us consider the case that a grating consisting of equally spaced lines shown

in Fig. 1(a) is deformed as shown in Fig. 1(b). The grating before deformation is

called ‘reference grating’ and the grating after deformation is called ‘specimen

grating’.

(a) (b)

(c)

(d)

Fig. 1. Theoretical explanation of moiré appearance showing equal-displacement contours:

(a) Reference grating; (b) Specimen grating; (c) Moiré fringe pattern obtained by superpos-

ing Figs. (a) and (b); (d) Moiré fringe pattern obtained by sampling of TV scanning lines or

digital camera

When the reference grating shown in Fig. 1(a) is superposed on the specimen

grating shown in Fig. 1(b), a new fringe pattern shown in Fig. 1(c) appers. The

fringe pattern is called ‘moire fringe’. A white moiré fringe line appears on the

parts where a black line of the reference grating and a black line of the specimen

grating are superposed or where a white line of the reference grating and a white

line of the specimen grating are superposed. A black moiré fringe line appears on

the parts where a black line of the reference grating and a white line of the speci-

men grating are superposed or where a white line of the reference grating and a

black line of the specimen grating are superposed.

230 Y. Morimoto and M. Fujigaki

When the specimen grating shown in Fig. 1(a) is recorded by a TV camera or a

digital camera, a moiré fringe pattern is also observed as shown in Fig. 1(d).

Scanning moiré method [22-33] or sampling moiré method [34-38] is used this

phenomenon.

Let us show the principle for obtaining displacement and strain distributions

from this moiré fringe pattern. Each white line from the left edges of the reference

grating is numbered as k=0, 1, 2, … as shown in Fig. 1(a). These numbers are

called ‘line number.’ By considering that the deformation is one-dimensional for

simplicity, each point moves along the x-direction, that is, normal to the original

grating line. Fig. 1(b) shows a deformed grating with x-directional deformation.

The lines of the deformed specimen grating are numbered as l=0, 1, 2, … respec-

tively, as shown in Fig. 1(b).

On a continuous moiré fringe line in Fig. 1(c), the difference between the line

number of the reference grating and the line number of the specimen grating is a

constant. The number m is the difference of the two line numbers.

m=k-l (1)

It is called ‘fringe order’ of the moiré fringe line. When the pitch of the grating

lines of the reference grating is p, the specimen grating is deformed as mp along

the line normal to the grating lines of the reference grating. That is, on the fringe

lines with moiré fringe order m, the displacement is mp. By looking at the moiré

fringe pattern, displacement distribution is determined. This is the principle of

moiré method to measure deformation.

That is, the x-directional displacement u at the place with a fringe order m is

expressed as follows:

u=mp (2)

The x-directional strain is defined as differentiation of the x-directional displace-

ment with respect to x. Then the strain is obtained as follows.

(3)

On the other hand, the fringe distance

between the neighboring fringes shows

that the displacement difference between the both ends of the distance is 1 pitch

of the reference grating. Therefore the strain at the distance is expressed as

follows.

)thanlargerlysufficient isWhen(

ndeformatiobeforelength

elongation

≅

−

(4)

From this equation, strain is obtained from the fringe space

Theory and Application of Sampling Moiré Method 231

When a grating is projected on an object, the grating is deformed according to

the shape of the object. When the reference grating is superposed on this deformed

grating, a moiré fringe pattern is observed. By analyzing this moiré fringe pattern,

the shape of the object is measured. This method is called ‘moiré topography’.

3 Phase Analysis of Grating or Fringe Pattern

In order to analyze a grating pattern or an optical interference pattern such as a

moiré fringe, image processing techniques such as thinning of lines to obtain frin-

ge center lines were used. It was time–consuming and the accuracy was not good.

Recently phase analysis is popular. It provides high-speed, automatic and accurate

analysis at each point of the object image. That is, the brightness distributions of a

grating pattern or a fringe pattern are regarded as cosinusoidal waves, and the pha-

ses at each pixel point of the object image is obtained from the brightness data of

the images [12-21]. The theory is as follows.

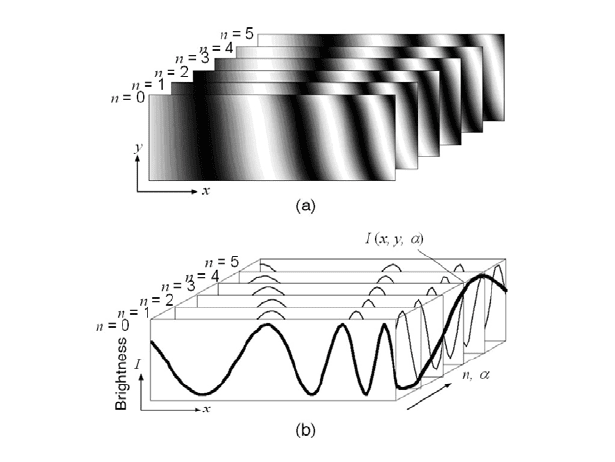
Fig. 2. Brightness and phase distribution of fringe pattern: (a) Brightness distribution; (b)

Wrapped phase distribution; (c) Unwrapped phase distribution

As shown in Fig. 2, the brightness distribution I(x, y) of a grating or a fringe

pattern is cosinusoidal, expressed as the following equation.

),()],(cos[),(),( yxIyxyxIyxI

(5)

232 Y. Morimoto and M. Fujigaki

where I

(x, y) and I

(x, y) are the brightness amplitude and the brightness of back-

ground at a point (x, y) in the image, respectively. When the phase of the grating

or fringe pattern is shifted, the brightness of the grating or the fringe pattern is ex-

pressed as follows:

),(]),(cos[),(),,( yxIyxyxIyxI

++=

αφα

(6)

where α is the phase-shift value obtained by moving the grating or the fringe pat-

tern. The wave has a phase at each pixel point, which is the 2

π ( = 360°) for one

cycle. The phase

is obtained from the fringe order m.

(7)

Fig. 3. Fringe patterns obtained by phase shifting method: (a) Brightness distributions ob-

tained by phase shifting; (b) Brightness distributions along centerline and brightness change

at edge point

If the phase shift α is given as 2πn/N, (n=0~N-1) i. e., N times for one cycle

and N images are obtained as shown in Fig. 3(a). That is, the brightness values I(x,

) are expressed in Fig. 3(a).

The brightness change at a pixel point expressed in Fig. 3 is cosinusoidal for

one cycle. The phase of the first image is the initial phase to obtain.

In order to analyze the initial phase

(x, y), several methods such as Fourier

transform method, phase-shifting method, extraction of characteristic, integral

phase-shifting method [19-21]

were proposed. These methods using phase analysis

are basically accurate.

Theory and Application of Sampling Moiré Method 233

The intensity of the n-th phase-shifted images I

(x, y) can be expressed as

follows:

),(]

),(cos[),(),( yxI

nyxyxIyxI

ban

++=

(8)

)1,...,1,0( −= Nn

The phase change at a pixel point of the fringe pattern can be obtained from the

frequency 1 of the discrete Fourier transform (DFT) or the phase-shifting method

using Fourier transform (PSM/FT) of Eq. (8). As the results, the wrapped phase

of the frequency 1 is expressed as follows [14,38].

tan

(x,y) =−

(x,y)sin(n

)

n= 0

N−1

∑

(x,y)cos(n

)

n= 0

N−1

∑

(9)

In Eq. (8), the three unknown values I

(x, y),

(x, y), I

(x, y) are obtained from

measuring more than three brightness values I

(x, y) and the initial phase

(x, y)

can be obtained using Eq. (9). By recording the grating in defocus of the camera if

the grating is not cosinusoidal, the recorded grating image is changed into a cosi-

nusoidal pattern approximately. Conventionally, N=3 or N=4 are used. However,

if larger N is used, the accuracy becomes better in the cases of noisy, non-

cosinusoidal and/or non-equal division of phase-shift.

The phase obtained by Eq. (9) is wrapped into -π π. The wrapped phase is

unwrapped by adding or subtracting 2π as shown in Fig. 2(c). In the case of moiré

fringe, the unwrapped phase

(x, y) =2πm is proportional to the displacement u as

sown in Eq. (2).

4 Measurement Method of Displacement and Strain by Phase

Analysis of Moiré Fringe

The moiré fringe order m is the difference of the specimen grating number l and

the reference grating number k as shown in Eq. (1). The phases of the moiré

fringe, the specimen grating and the reference grating are obtained by multiplying

2π to the moiré fringe order and the grating numbers. Then Eq. (1) becomes as

follows.

srm

lkm

φφππφ

−=−== )(22 (10)

where

is the phase of the moiré fringe,

is the phase of the specimen grating,

and

is the phase of the reference grating. From Eq. (10),

(11)

234 Y. Morimoto and M. Fujigaki

If the phase

is analyzed when the phase

is given, the phase

of the speci-

men grating is calculated.

When the phase

of the sampling is shifted by 2π, i.e., one pitch of the refer-

ence grating, the phase

of the moiré fringe is shifted by 2π. When the phase of

the moiré fringe is also changed by the deformation, the phase difference

Δφ

the grating lines is the same as the minus of the phase-difference

Δφ

of the moiré

fringe before and after deformation at a pixel point.

Even if the grating is already deformed in the initial state, the displacement u

after the initial state is obtained from the phase difference of moiré fringes Δ

be-

tween before and after deformation. Then the displacement u is obtained as the

following equation from Eqs. (1) (3), (10).

)(

121212 ssmm

pmmu

φφ

−−=−=−= (12)

ppu

−=

= (13)

)(

−=

== (14)

where, the suffix, 1 and 2 are express before and after deformation, respectively.

In the case of fringe order analysis, the fringe orders and the distances of

neighboring fringes are given as integer numbers. And the number of data is few,

because the data are given one between the fringe distance. While, phase analysis

is very accurate because the data are given at every pixel point and the phase is

given as decimal. Practically the accuracy of phase analysis is 100 to 1000 times

better than the one by fringe distance analysis. The analysis algorithm is very sim-

ple and the process is same at all the pixel points.

5 Sampling Moire Method (Scanning Moire Method)

5.1 Background of Sampling Moiré Method

Moiré fringe appears by sampling with a digital camera as shown in Fig. 1(d). The

phenomenon is called ‘scanning moiré method’ because the moiré pattern appears

by sampling of scanning lines of a TV camera [22-33]. The authors applied this

method to two-dimensional analysis of a 2-D grating with x- and y-directional

gratings using a digital camera or an image processor which samples an image at

each pixel point. A moiré fringe pattern is obtained by changing the sampling

pitch of the recorded image. Therefore this method is called ‘sampling moiré

method’ [34-38].

Theory and Application of Sampling Moiré Method 235

Let us explain the history of scanning moiré method and sampling moiré

method.

Idesawa et. al. [22] proposed scanning moire method by changing the scanning

pitch ellectorically. Morimoto et. al. [23,24]

proposed sanning moire method by

thinning-out the scanning line of a TV camera using an image processor. Arai et.

al. [25,27,29] proposed phase-shifting scanning moire method using thinning-out

and interpolation and discussed the accuracy according to the interpolation me-

thod. Yoshizawa et. al. [26]

proposed a phase analysis method measuring the pha-

se difference at two points electoronically using rotating reference grating. Mori-

moto et. al. [28,31-33]

also proposed a method to obtain smooth moire fringe

pattern by shifting the thinning-out of scanning lines. Kato et. et. al. [30]

proposed

a real-time shape measurement system by low-pass filtering and superposing a

phase-shited virtual reference grating on a recorded specimen grating. The authors

[34-38] analyzed shape, displacement and strain distributions using the interpola-

tion method developed by Arai et. al.

Conventional phase-shifting method requires multiple phase-shifted images.

However, sampling moire method requires only one image. From the one image,

phase-shifted moire patterns are obtained by changing the start pixel of sampling,

and then it is possible to analyze a moving object.

If a two-dimensional grating with

x- and y-directional gratings is used, two di-

mensional deformation analysis can be performed. In this case, by eliminating one

directional grating with averaging in the other directional grating for one pitch,

one directional analysis is performed by the one-dimensional sampling moire me-

thod mentioned above. By changing the direction, two-dimensional analysis is

performed. The processes are as follows.

5.2 Process of Sampling Moiré Method Using 1-D Grating

A grating pattern is recorded by a digital camera. The recorded image is analyzed

by sampling moiré method. The process is as follows.

Figure 4 illustrates the appearance of a moiré fringe pattern by sampling moiré

method. Figure 4(a) shows the center position of the sampling points (pixel points)

of a digital camera. Figure 4(b) shows a specimen grating. The image of Fig. 4(b)

recorded by the camera is shown in Fig. 4(c). The image shows only the original

grating, not a moiré fringe pattern. If every

N-pixel (in this case, thinning-out in-

dex

N = 4) from the first sampling point is picked up from Fig. 4(c), a moiré fringe

pattern is obtained as shown in Fig. 4(d). Figure 4(d) is obtained by selecting the

first pixel and sampling every

Nth -pixel (in this figure, N = 4). If instead the sec-

ond, third or fourth sampling point is selected, the images of a moiré fringe pattern

with

π/2, π and 3π/2 phase-shift shown in Fig. 4(e), (f) and (g), respectively, are

obtained. This process corresponds to the phase shifting of the fringe pattern. If all

the sampled images that are thinned-out in Figs. 4(d)-(g) are interpolated using the

neighboring data, the image becomes clearer and easy to observe as shown in

Figs. 4(h)-(k) from Figs. 4(d)-(g), respectively. From these phase-shifted fringe

patterns, the phases of the moiré fringes are analyzed.

236 Y. Morimoto and M. Fujigaki

Fig. 4. Phase analysis by sampling moiré method: (a) Sampling points of camera; (b)

Specimen grating; (c) Sampled image of Fig. (b); (d) Thinned-out image from Fig. (c)

(N=4, α=0); (e) Thinned-out image from Fig. (c) (N =4, α=π/2); (f) Thinned-out image

from Fig. (c) (N =4, α=π); (g) Thinned-out image from Fig. (c) (N =4, α=3π/2); (h) Interpo-

lated image of Fig. (d); (i) Interpolated image of Fig. (e); (j) Interpolated image of Fig. (f);

(k) Interpolated image of Fig. (g)

When the number of phase-shifting for one cycle is N, and the intensity of the

n-th phase-shifted images I

(x, y), the wrapped phase

is obtained from Eq. (9).

If the phase

of the moiré fringe is analyzed when the phase

of the refer-

ence grating i.e. sampling phase is given, the phase

of the specimen grating is

determined from Eq. (11).

From the phase

of the specimen grating, shape, displacement and strain is

accurately obtained according to the optical systems, respectively.

In this case, the gage length is one or two pitches of the grating. It is smaller

than Fourier transform method which uses whole data of the image. In the sam-

pling moiré method, the phase analysis of moiré pattern provides accurate result of

displacement of the grating. If the number of the phase-shifted moiré patterns i.e.,

the number of pixels for a pitch of the grating is larger, the resolution of phase

analysis becomes more accurate but the spatial resolution becomes worse.

5.3 Process of 2-D Displacement Analysis by Sampling Moiré Method Using

2-D Cross Grating

In order to analyze two-dimensional (2-D) displacement, a 2-D cross grating is used.

Figure 5 shows images in the 2-D analysis process by sampling moiré method.

Figure 5(a) shows the image of a 2-D grating captured by a CCD camera. Figure 5(b)

Theory and Application of Sampling Moiré Method 237

shows the extracted

x-directional grating pattern obtained by averaging (smoothing)

of Fig. 5(a) in the

y-directional one pitch. Figure 5(c) shows several phase-shifted

moiré patterns which are produced by sampling moiré method from Fig. 5(b).

Figure 5(d) shows the phase distribution of the moiré pattern produced from Fig.

5(c) by phase-shifting method using Eq. (9). Figure 5(e) shows the phase distribu-

tion of the reference grating which is smoothed in the

y-direction from the 2-D cross

grating pattern. From the phase distribution

of the moiré, and the phase distribu-

tion

of the reference grating, the phase distribution

of the deformed specimen

grating can be calculated using Eq. (11). Figure 5(f) shows the wrapped phase distri-

bution of the deformed specimen grating.

Fig. 5. Process of x-directional phase analysis using 2-D grating

The period of the reference phase distribution is usually taken as same as the

pitch of sampling pixels in sampling moiré method. Figure 2(g) shows the

directional unwrapped phase distribution. In the same manner, the y-dimensional

phase distribution of the specimen grating can be obtained.

6 Deflection Measurement by Sampling Moiré Method

The sampling moiré method proposed above was applied to the measurements of

shape, displacement and so on. The deflection distribution of a three-point-

bending beam was measured by one camera system [36,38]. The sampling moiré

method using phase shifting was applied to the deflection measurement of a beam

under symmetric three-point bending. Conventional deflection measurement of

bridges is usually performed by using many deflection sensors for point-by-point

238 Y. Morimoto and M. Fujigaki

measurement. It is time-consuming, hard-working and expensive for distribution

measurement. The sampling moiré method is very useful for the measurement be-

cause of high-accuracy, high-speed, low-cost and easy implementation.

6.1 Experimental Setup and Grating Tape

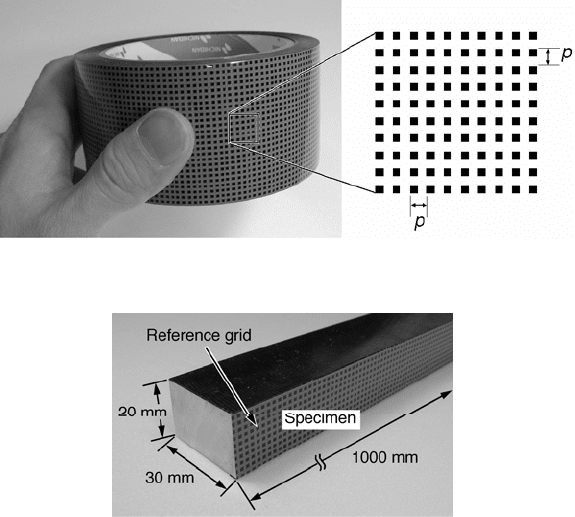
A special tape of a two-dimensional cross grating with 2.0 mm pitch shown in

Fig. 5 was pasted over the steel beam (SS400) as shown in Fig. 7. The size of the

beam is 30 mm in width, 20 mm in height and 1000 mm in length. The experimen-

tal setup is shown in Figs. 8 and 9. A normal digital camera (Nikon, E8800), with

3264 pixels by 2448 pixels resolution, was used to record the image. The distance

from the specimen to the camera was 990 mm as shown in Fig. 8(b). The camera

was aligned so that its seven pixels were corresponding to the grating pitch.

The specimen was loaded by increasing the number of 1.0 kg weight blocks.

The steel beam was loaded at the center position from 9.8 N to 127.4 N. To check

the actual displacement of the specimen, a laser displacement sensor with 0.02

μm

resolution accuracy was located at the position of the loading point.

In recorded images, one pixel of the digital camera was adjusted to correspond

to about 0.3 mm on the beam.

Fig. 6. Tape with grating for deformation measurement. (Pitch p = 2.032 mm)

Fig. 7. Steel beam specimen, Size: 30 mm (W), 20 mm (H) and 1000 mm (L)